A quasi-isentropic model of a cylinder driven by aluminized explosives based on characteristic line analysis

Hong-fu Wng ,Yn Liu ,b,*,Fn Bi ,Jun-bo Yn ,Xu Li ,Feng-lei Hung

a State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

b Beijing Institute of Technology Chongqing Innovation Center,Chongqing,401120,China

Keywords:Aluminized explosives Cylinder experiments Quasi-isentropic model Characteristic line analysis Reaction degree of Al powder Physical parameters of detonation products

ABSTRACT A quasi-isentropic study on the process of driving a cylinder with aluminized explosives was carried out to examine the influence of the aluminum(Al)reaction rate on cylinder expansion and the physical parameters of the detonation products.Based on the proposed quasi-isentropic hypothesis and relevant isentropic theories,the characteristic lines of aluminized explosives driving a cylinder were analyzed,and a quasi-isentropic model was established.This model includes the variation of the cylinder wall velocity and the physical parameters of the detonation products with the Al reaction degree.Using previously reported experimental results,the quasi-isentropic model was verified to be applicative and accurate.This model was used to calculate the physical parameters for cylinder experiments with aluminized cyclotrimethylenetrinitramine explosives with 15.0%and 30.0%Al content.The results show that this quasi-isentropic model can be used not only to calculate the cylinder expansion rule or Al reaction degree,but also to calculate the physical parameters of the detonation products in the process of cylinder expansion.For explosives with 15.0%and 30.0%Al,24.3%and 18.5%of the Al was found to have reacted at 33.9 μs and 34.0 μs,respectively.The difference in Al content results in different reaction intensity,occurrence time,and duration of two forms of reaction(diffusion and kinetic)between the Al powder and the detonation products;the post-detonation burning reaction between the Al powder and the detonation products prolongs the positive pressure action time,resulting in a continuous rise in temperature after detonation.

1.Introduction

In research into high energy explosives,high power is one of the main goals,and adding metal particles into explosives is an important way to improve their power.At present,aluminized explosives account for a large proportion of those used in highpower military applications[1-5].Al powder improves explosive power in two main ways:firstly,a Al oxidation reaction gives off a large amount of heat,increasing the heat produced by detonation and the total energy of an explosive;secondly,the Al oxidation reaction changes the process of the release of the explosive detonation energy,prolonging the duration of energy release and improving the work capacity of an explosive[6-8].It is very difficult to greatly improve the energy per unit volume of currently existing explosives,but optimizing their energy output structure can make them release their energy and exert their power more effectively.Studying the detonation characteristics of aluminized explosives and the reaction mechanism of the Al powder in the detonation products can optimize their formulation,improve their energy-output structure,and enhance their power[2,4,7,9,10].

The current understanding of the detonation mechanisms of aluminized explosives is mainly based on the secondary reaction theory proposed by Cook et al.[11].In this theory,the Al powder does not generally participate in the reaction at the Chapman-Jouguet(CJ)plane,but absorbs heat to reduce the energy of the wave front used to support detonation propagation;a reaction between the Al powder and the detonation products takes place after the acoustic interface,and the energy generated can enhance the expansion power of the detonation products.Kato et al.[12]used pressure sensors to measure the detonation pressure of aluminized explosives.They found that when the particle size of the Al powder is 8.0 μm,about 2.5 μs after the precursory shock wave,the Al oxidation reaction makes the detonation pressure rise and the reaction zone widen.Pahl et al.[13]measured the detonation velocity,detonation pressure,and detonation temperature of aluminized explosives.Their results showed that there is a secondary release of energy after detonation,indicating that the Al powder will react after the CJ plane for a period of time.Nevertheless,some researchers believe that the Al can react at the CJ plane during the detonation to provide energy for detonation propagation[14].

In the calculation model proposed by Miller[15],the reaction process of aluminized explosives is divided into two stages.The first of these is the CJ reaction stage:strong chemical reactions occur in the base explosives,and a small part of the Al powder participates in these reactions.The second stage is the aftereffect reaction stage:most of the Al powder reacts in this stage to form the final products.Victorov[16]calculated the detonation velocities of cyclotetramethylenetetranitramine (HMX), cyclotrimethylenetrinitramine(RDX),and bis(trinitroethyl)nitroamine(BTNEN3)using Howard"s nonlinear detonation model and the Wood-Kirkwood dynamic model.It was found that Al reacted wholly or partially in the reaction zone.Finger et al.[17]studied the work capacity of aluminized plastic-bonded explosives(PBX)and pointed out that when the size of the Al powder particles is less than 200.0 μm,the detonation process will be affected.Miller[15]found that for the underwater detonation of aluminized explosives,a considerable fraction of the energy is released in the secondary reaction process behind the CJ plane.Miller therefore proposed a detonation reaction model for aluminized explosives that gave the combustion reaction rate of the Al powder behind the CJ plane.He combined this with the Jones-Wilkins-Lee(JWL)equation of state(EOS)to obtain the EOS of the detonation products.

The metal cylinder experiment is one of the standard methods for evaluating the ability of an explosive to accelerate a metal.Cylinder experiments with aluminized explosives ignore the influence of the initiation mode,which is convenient for evaluating the secondary reaction of the Al powder[18-20].Chen et al.[21]found that,compared with cylinder specimens made of titanium alloy and high-strength steel,the plasticity and ductility of oxygenfree copper were relatively high,and the consistency of the test values was better.High ductility can delay the cylinder expansion time and enlarge the width of the secondary Al reaction zone.Shen et al.[22]found that the cylinder expansion process can only last for about 20.0 μs in a 25.0-mm cylinder experiment with aluminized RDX,while in a 50.0-mm cylinder experiment,the cylinder expansion time can reach about 40.0 μs.Hu and Sun[23]analyzed the detonation products of aluminized RDX explosives and found that when the Al content exceeded 30.0 %,the alumina content in the detonation products did not increase.Pei et al.[18]carried out 50.0-mm cylinder experiments using aluminized RDX with 15.0 %and 30.0 % Al.Their experimental results showed that the explosives with a 15.0 % Al content had a greater work capacity in the time range recorded.Liu et al.[24]found that,for aluminized hexanitrohexaazaisowurtzitane(CL-20)explosives with 15.0 % Al content,when the particle size of the Al powder was in the range 2.0 μm-50.0 μm,the effect of size change on the acceleration ability of the explosives was not obvious,and the reaction behavior of the Al powder and detonation products was similar.However,when the Al content was reduced from 15.0% to 5.0 %,they found that changing the Al particle size had a greater effect on the acceleration ability of the explosives.

In recent research into aluminized explosives using cylinder experiments,the theoretical considerations have mainly focused on the dynamic response of the Al particles under the action of detonation waves and the reaction between the Al and the detonation products.However,due to the secondary Al oxidation reaction that occurs in aluminized explosives after detonation,the isentropic theory,which is widely applied to ideal explosives,is not suitable for cylinder experiments with aluminized explosives.The isentropic theory therefore seldom applied to aluminized explosives.The effective acting time in cylinder experiments is no more than 40.0 μs,but Al powder requires hundreds of microseconds to react completely after explosive detonation[25].Therefore,it is necessary to establish a quasi-isentropic model describing the secondary Al oxidation reaction for cylinder experiments with aluminized explosives.

In this study,the characteristic line of aluminized explosives driving a cylinder was analyzed,and a quasi-isentropic model was established for this system using the relevant isentropic theories and the deduced relationships between the detonation parameters and the reaction degree of the Al powder.This model includes the variation of the cylinder wall velocity,the detonation parameters on the inner wall of the cylinder and at other positions with the Al reaction degree as the cylinder expands,and the relationships between the pressure and temperature of the detonation products and the Al reaction degree after the cylinder is completely broken.

2.Hypothesis of the quasi-isentropic model

The schematic diagram of the cylinder experiments with aluminized explosives is shown in Fig.1,the principle of the experiments is that the detonator initiates the explosive lens,the conduction triggers the probe,and then the pulsed constantcurrent source begins to supply power for the laser probe.After the shock waves pass through the explosive lens,they become flat detonation waves.The flat detonation waves initiate the booster pellet,and then produce stronger detonation wave to initiate the aluminized explosive.When the cylinder is driven by aluminized explosives,the expansion velocity of the outer wall is recorded by the laser probe.

The cylinder driven by the detonation products of aluminized explosives is shown in Fig.2,the detonation wave propagates to the right with velocityD,and the detonation products behind the detonation wave expand rapidly to the left.There is a cluster of right-propagating sparse waves which follow the detonation wave,the first sparse wave(i.e.wave head)following the detonation wave propagates to the right with velocityD.The detonation products have the characteristics of high temperature and high pressure,and the cylinder blocks the diffusion of detonation products and Al powder,Al powder reacts rapidly with detonation products to form pressure gradient,and then the sparse disturbance is enhanced.The diameter effect caused by the expansion motion of the cylinder wall leads the sparse wave near the cylinder wall to be curved.For the quasi-isentropic model established in this paper,the x-axis is perpendicular to the right-propagating sparse wave front,and any x position in the cylinder is completely coincident with the rightpropagating sparse wave front,as shown in Fig.2.

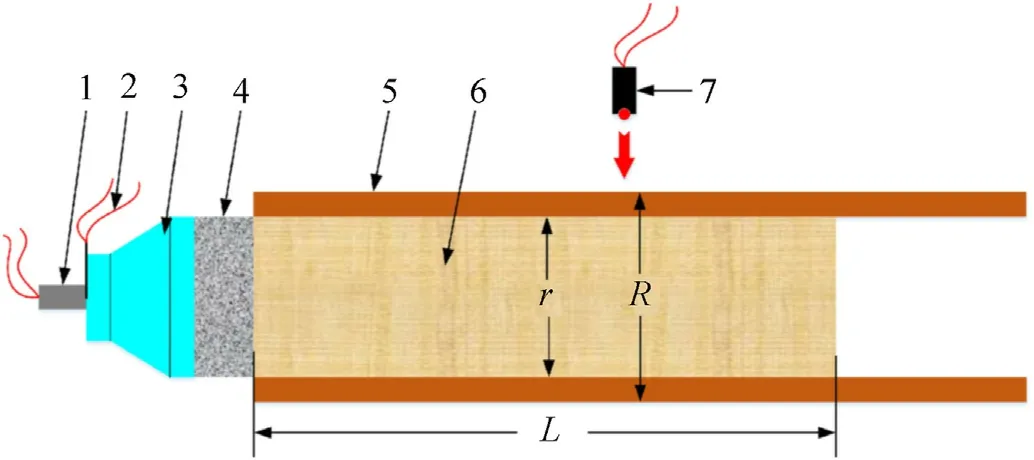
Fig.1.Schematic diagram of the cylinder experiments with aluminized explosives.1-Detonator;2-Probe;3-Explosive lens;4-Booster pellet;5-Cylinder;6-Aluminized explosive;7-Laser probe.

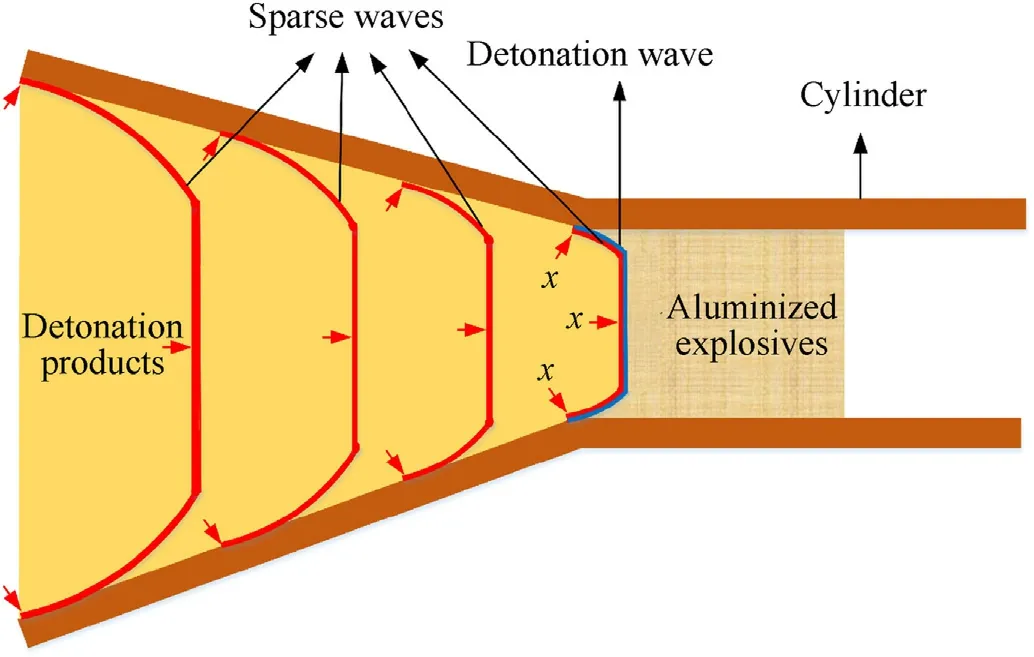
Fig.2.Detonation product of aluminized explosives driving cylinder.

2.1.Reaction process of aluminized explosives

In cylinder experiments with aluminized explosives,the cylinder expansion process is divided into two stages:an Al nonreaction stage and a secondary reaction stage after detonation.The Al non-reaction stage includes the detonation process(the 0-L/Dphase in Fig.3,whereLis the length of the aluminized explosives along thex-axis,andDis the detonation velocity of the aluminized explosives)and the preparation process of the Al oxidation reaction after detonation(L/D-t1phase in Fig.3).Whent=t1,the Al powder begins to react,and the cylinder expansion process enters the secondary reaction stage,which is divided into as many very short time intervals as possible.The following assumptions are made:

1.The Al powder does not participate in the detonation reaction at the CJ plane,and an Al oxidation reaction takes place after a period from the CJ plane.

2.The Al powder that reacts in the time intervalti-ti+1reacts completely with the detonation products in a single instant atti.

3.After the Al oxidation reaction is completed atti,the reaction products retain isentropic flow in theti-ti+1time interval.

4.In theti-ti+1time interval,after the complete reaction of the Al powder atti,the physical parameters of the reaction products change fromu1ti,c1ti,P1ti,ρ1ti,T1ti,d1ti,B1ti,A1titou2ti,c2ti,P2ti,ρ2ti,T2ti,d2ti,B2ti,A2ti(the representative meanings of these symbols will be described in the next section),and the cylinder does not expand during the reaction.After the Al oxidation reaction,the products undergo isentropic expansion,and the cylinder expands with the isentropic flow of products.After isentropic expansion,the physical parameters of the reaction products change fromu2ti,c2ti,P2ti,ρ2ti,T2ti,d2ti,B2ti,A2titoumti,cmti,Pmti,ρmti,Tmti,dmti,Bmti,Amti.

5.The detonation products move at the constant velocityumtiin theti-ti+1time interval,the total movement distance of the products at the right end of the charge along the length of the cylinder isZi+1atti+1,when the right-propagating sparse waves reach the right end of the detonation products(x=L+Zi+1)atti+1,there will be a cluster of new left-propagating sparse waves propagating into the detonation products;then the products move at the uniform velocity in theti+1-ti+2time interval.

6.The process is divided into as many time intervals as possible,making each time interval very short to ensure the rationality of the above assumptions.

7.The Al powder is evenly distributed throughout the explosives,and an Al oxidation reaction occurs between the Al powder and detonation products.

8.The influence of heat exchange between the experimental system and the outside on entropy is not considered;after the oxidation reaction of the Al powder,the entropy of the system changes due to the cumulative effect of each small time interval.

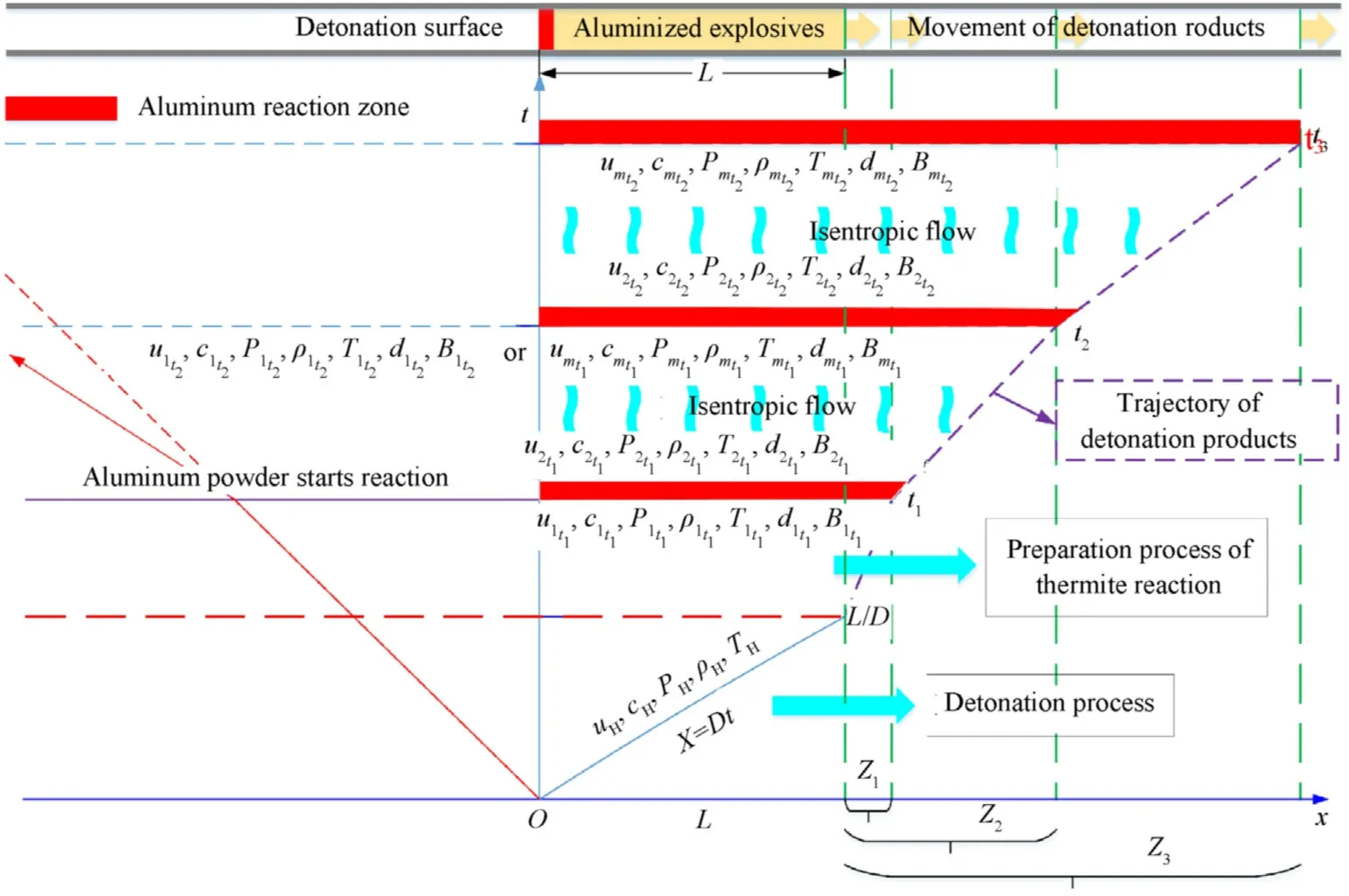
Fig.3.Hypothesis of the quasi-isentropic model for cylinder experiments with aluminized explosives.

9.It is assumed that the material of the cylinder wall is incompressible,and the volume of the wall material remains constant during cylinder expansion.

Note that in the above description,the symbols with subscripts 1tiandmti-1represent exactly the same respective parameters.These parameter values are expressed with two symbols to conveniently describe the physical and chemical processes in each time interval.Furthermore,each time interval can be independent to facilitate the derivation and generalization of equations.

2.2.Proportional relationships between physical parameters in adjacent time intervals

In this section,we establish the proportional relationships between the physical parameters in adjacent time intervals.The detonation product pressure of aluminized explosives is influenced by the detonation reaction of the ideal explosive(IE)components and the oxidation reaction of the Al powder.The Al powder does not participate in the detonation process,which dilutes the explosives.Therefore,the EOS for an ideal gas can be used to describe the contribution of IE detonation reaction to the product pressure:

When the Al powder begins to react with the detonation products,and according to Ref.[26],the Noble-Abel EOS is used to describe the contribution of Al oxidation reaction to the product pressure:

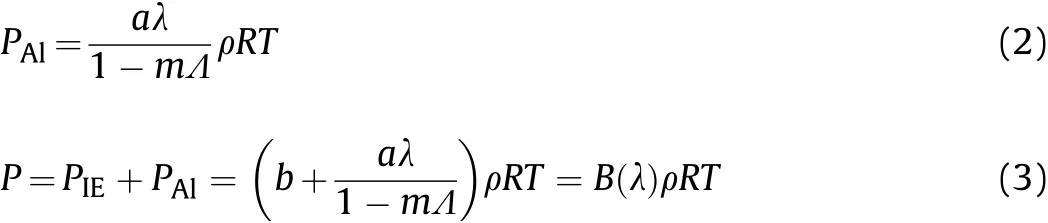
where:PIEis the contribution to the detonation product pressure due to the IE detonation;PAlis the contribution to the detonation product pressure due to the Al oxidation;aandbare the initial mass fractions of the Al powder and ideal explosive,respectively;Ris the gas constant,R=R0/M,in whichR0is the universal gas constant andMis the molar mass of the detonation products;λ is the reaction degree of Al;Pis the pressure of the detonation products;ρ is the density of the detonation products;Tis the temperature of the detonation products;mis the number of moles per unit volume of the detonation products;and Λ is an empirical constant.

The isentropic formula for aluminized explosives is obtained by taking the power of γ on both sides of Eq.(3)and dividing byPiγ-1,as shown in Eq.(6):

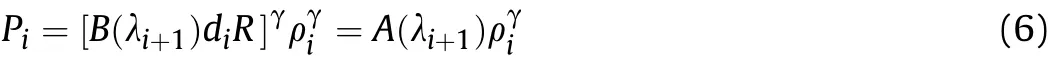
where,

Piis the pressure of the detonation products in theti-ti+1stage;ρiis the density of the detonation products in theti-ti+1stage;Tiis the temperature of the detonation products in theti-ti+1stage;λi+1is the reaction degree of Al in thet1-ti+1stage,B（λi+1）is a coefficient related to λi+1in thet1-ti+1stage,which can be simplified asBi+1,andA（λi+1）is a coefficient related to entropy and λi+1in thet1-ti+1stage,which can be simplified asAi+1.

Based on the reaction process of aluminized explosives in Sec.II.A,the sound velocity is affected by the change ofAiand γ caused by Al reaction atti,so supposeα is coefficient related to the change of γ in Al reaction stage,that is,the influence factor of Al reaction on γ of aluminized explosives is extracted and equal to α,so γ is still equal to the isentropic index of ideal explosives aftert1,the isentropic index of ideal explosives is generally taken as 3.According to the isentropic formulas of two adjacent time intervals:

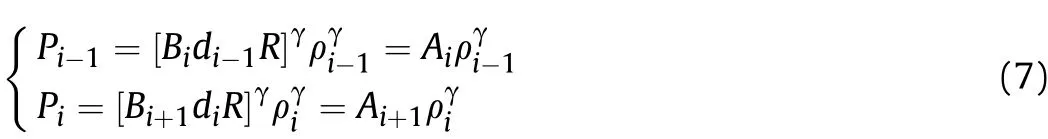
and the isentropic sound velocity formulawe can derive

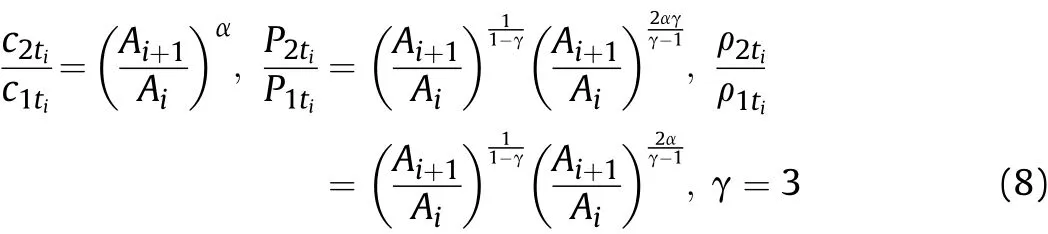
where:c1tiandc2tiare the sound velocities in the detonation products before and after the Al oxidation reaction atti,respectively;AiandAi+1are coefficients related to the entropy and Al reaction degree in thet1-tiandt1-ti+1stages,respectively,and these represent effective factors for the influence of Al oxidation reaction on the physical parameters in the two stages;P1tiandP2tiare the pressures of the detonation products before and after the Al oxidation reaction atti,respectively;ρ1tiand ρ2tiare the densities of the detonation products before and after the Al oxidation reaction atti,respectively.

In order to distinguish the non-reaction stage and the reaction stage of Al,γ=3 is substituted into the Al non-reaction stage as shown in Sec.III-IV;in the Al reaction stage,although γ=3,the symbol γ is used to represent the isentropic index as shown in Sec.V-VII.

He very soon found out that in addition to her natural indolence, she was being as much indulged and spoilt day by day as if the Fairy had been her grandmother, and was obliged to remonstrate17 very seriously upon the subject

According to Eq.(3)and the derivations of pressurePand density ρ in Eq.(8),the proportional relationships betweenT2tiandT1tiand betweend2tiandd1tiin adjacent time intervals can be obtained as

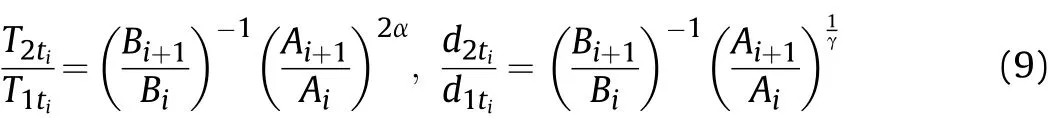
where:T1tiandT2tiare the temperatures of the detonation products before and after the Al oxidation reaction atti,respectively.

It is assumed that,after the Al oxidation reaction is completed at the initial moment of each time interval,the disturbance propagates to the detonation products at the velocityDi=ui+cialong the direction of fluid flow during the remainder of each time interval.According to the Hugoniot equation and the Rayleigh equation,can be obtained,soand the proportional relationship betweenu2tiandu1tiin two adjacent time intervals is obtained as

where:Diis the propagation velocity of the right-propagating sparse waves in theti-ti+1stage;uiis the particle velocity of the detonation products in theti-ti+1stage;ciis the sound velocity in the detonation products in theti-ti+1stage;andu1tiandu2tiare the particle velocities of the detonation products before and after the Al oxidation reaction atti,respectively.

To make the proportional relationships of the physical parameters in adjacent time intervals conform to the related basic theories and facilitate subsequent accurate derivation,Eqs.(8)-(10)were derived fromthe isentropic formula,and the isentropic sound velocity formula.Since λiis a monotonically increasing function with time,according to Eqs.(3)and(6),Bi＜Bi+1andAi＜Ai+1,which means that the entropy of detonation products increases with the reaction of Al;and if the Al powder does not react atti,then atti:Ai+1=Aiandwhich shows that the hypothesisis reasonable.The calculated results based on this hypothesis are in good agreement with the experimental results in Sec.VIII,which shows that the hypothesisis correct.

3.Characteristic line analysis in zone I and zone II

Based on the hypothesis of the quasi-isentropic model,the characteristic lines for cylinder experiments with aluminized explosives can be analyzed as shown in Fig.4.Whent＜t1,the Al powder does not participate in the reactions,so the deflection of the characteristic lines is not affected.Whent=L/D,the detonation wave reaches the right end of the aluminized explosivesL,and there will be a cluster of new left-propagating sparse waves propagating into the detonation products.Whent≥t1,the rightpropagating sparse waves reach the right end of the detonation productsL+Zi(Ziis the movement distance of the right end of the detonation products atti)atti,there will be a cluster of new leftpropagating sparse waves propagating into the detonation products;the Al powder that reacts in theti-ti+1time interval reacts completely with the detonation products in an instant atti.Due to the influence of the Al oxidation reaction,the characteristic lines deflect atti.A characteristic line analysis of the physical parameters for these experiments is shown in Fig.5.

In Fig.5,Zones I and II correspond to the phase in which the Al powder does not participate in the reactions,and this includes the detonation process(as shown in Fig.3,0-L/Dstage)and the preparation process of the Al oxidation reaction after detonation(as shown in Fig.3,L/D-t1stage).In the detonation process,the sound wave propagation speed is so fast that there is not enough time for the heat of the disturbed medium to be transmitted into the surrounding medium.Therefore,the sound wave propagation process can be regarded as isentropic,as shown in Eq.(11-a);for ideal fluids,the isentropic formula is shown in Eq.(11-b),in whichA（s）is a constant depending on the initial entropy value and γ is the isentropic index;in isentropic flow,the continuity equation and the momentum equation are shown in Eq.(11-c)and(11-d),respectively.When Eq.(11)are solved and the value of γ is 3,the solution results are as shown in Eq.(12).The state(or disturbance)determined by（u+c）propagates along the fluid-flow direction(i.e.,along the positive direction of thexaxis)with velocity dx/dt=u+c,while the state determined by（u-c）propagates against the fluid-flow direction with velocity dx/dt=u-c.

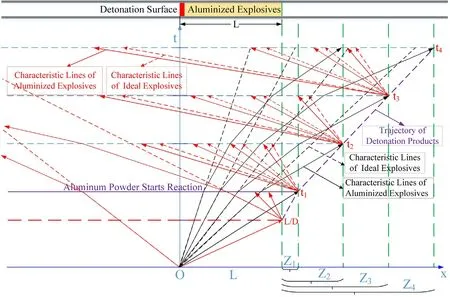
Fig.4.Characteristic line analysis of cylinder experiments with aluminized explosives.

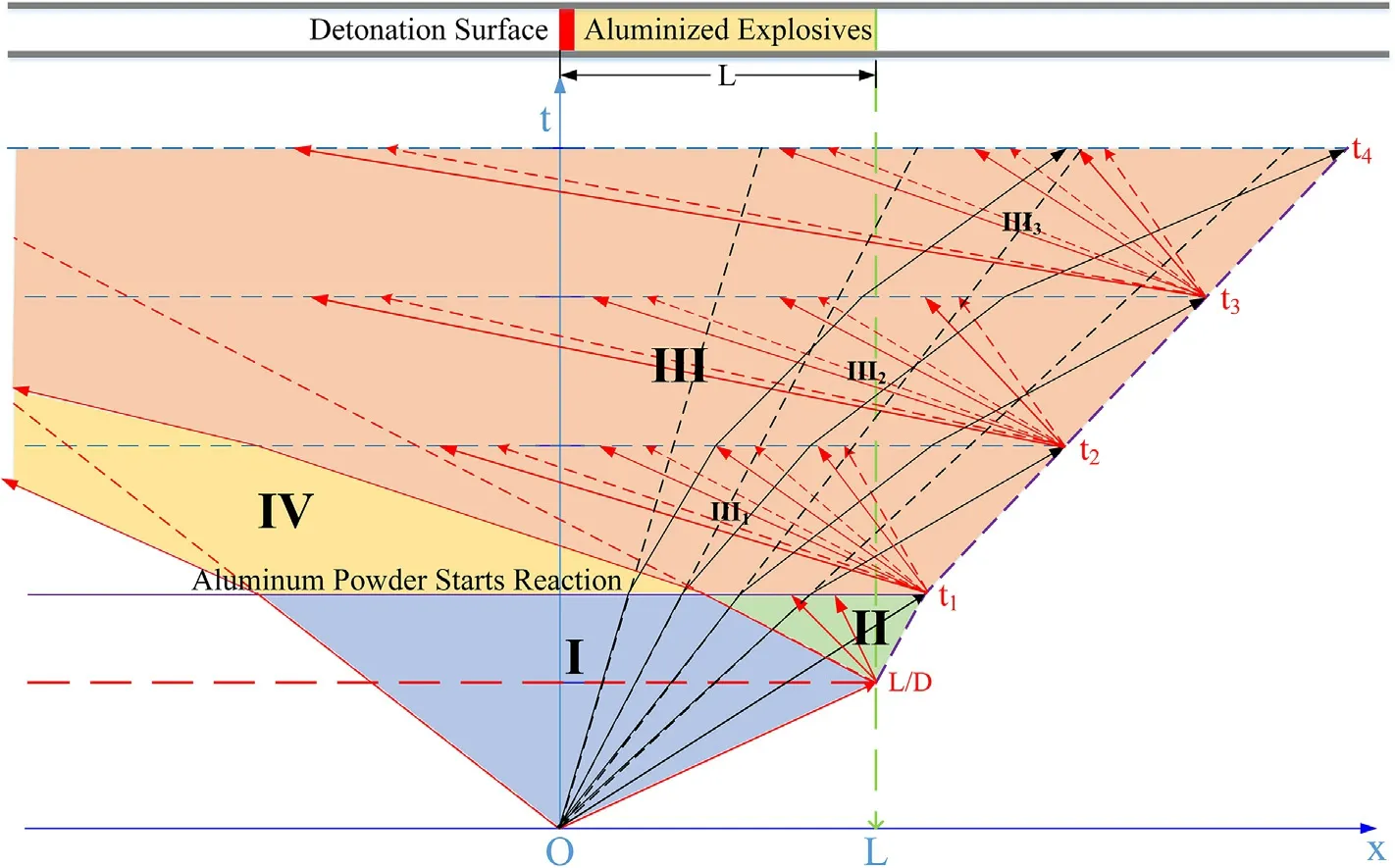
Fig.5.Physical parameter analysis for cylinder experiments with aluminized explosives.

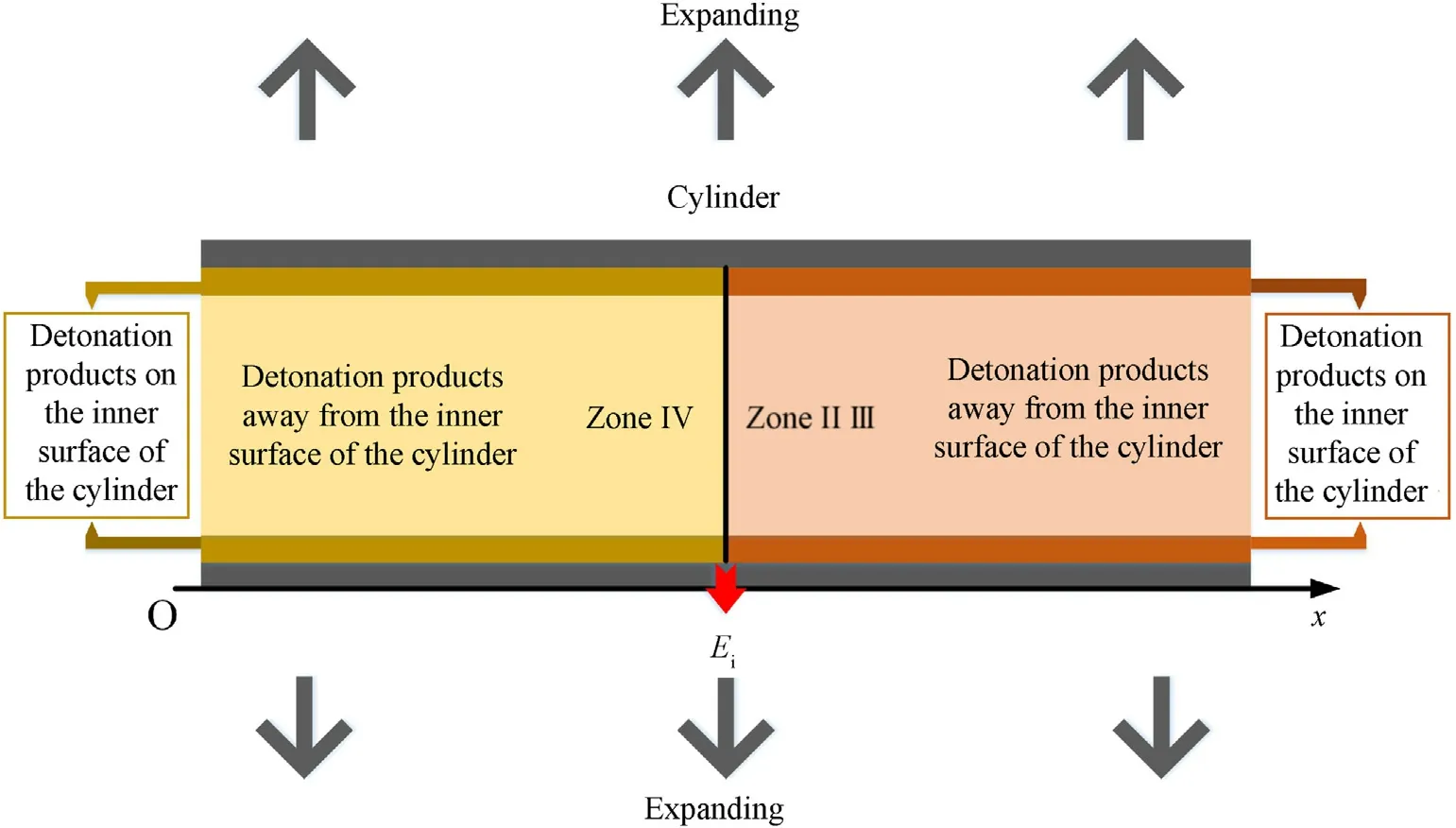
Fig.6.Detonation product analysis for cylinder experiments with aluminized explosives.

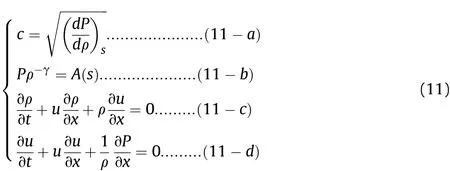
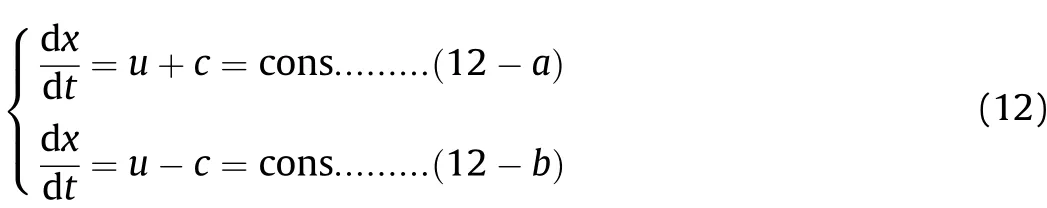
In Eqs.(11)and(12):Pis the pressure of the detonation products in the cylinder;ρ is the density of the detonation products in the cylinder;cis the sound velocity of the detonation products in the cylinder;uis the particle velocity of the detonation products in the cylinder;tis the time;andxis the position to be analyzed on thexaxis along the length of the cylinder.

The left end of the aluminized explosives is the initiation surface and set as the origin of the x-axis.After initiation and before the detonation wave reaches the right end of the explosives,i.e.,under the conditiont≤L/D,there is only a cluster of right-propagating sparse waves.Whent=L/D,the detonation wave reaches the right endL.At this time,there will be a cluster of new leftpropagating sparse waves propagating into the detonation products.The characteristic equation of these sparse waves is

When the initial conditions aret=L/Dandx=L,substituting these into the above equation gives

Since there is already a cluster of right-propagating sparse waves in the input area of the left-propagating sparse waves,there are two clusters of waves flowing in opposite directions.This can be described by

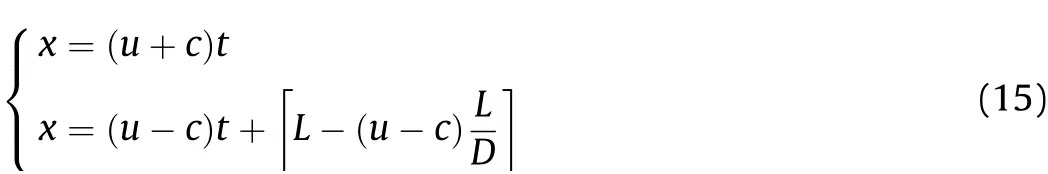
The left-propagating wave head moves at the velocity（u-c）=in the area disturbed by the right-propagating sparse waves,so it reaches positionx(xis the position to be analyzed along the length of the cylinder)at time

At the same time,according to the CJ parameters(cH,PH,ρH)of the detonation wave front,the isentropic sound velocity[Eq.(11-a)]and the isentropic formula[Eq.(11-b)],the variation rules of the detonation product pressurePand density ρ in the cylinder are

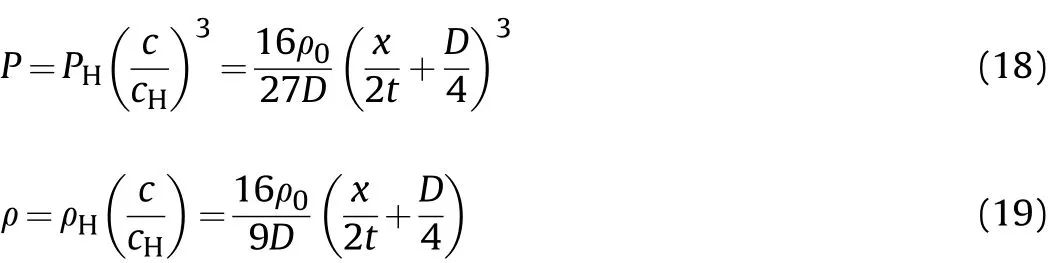
where:cHis the sound velocity in the detonation products at the CJ plane;PHis the pressure of the detonation products at the CJ plane;and ρHis the density of the detonation products at the CJ plane.

The temporal and spatial distributions of the detonation product pressurePand density ρ in the cylinder are

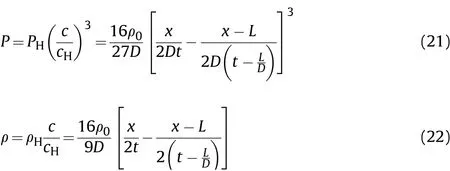
The movement distance of the right end of the detonation products isZ1att1,we get

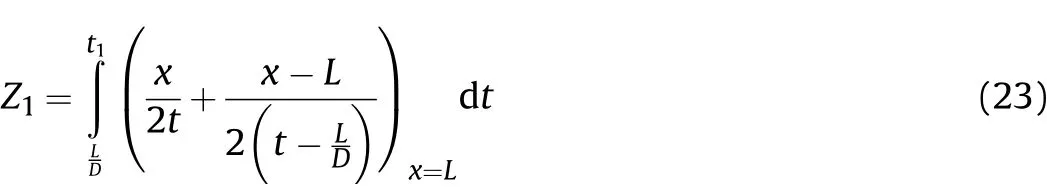
The above characteristic line analysis of Zone I and II is based on a rigid cylinder wall,and there is no expansion movement in the detonation process.However,this is inconsistent with the actual situation of the cylinder experiments.In reality,the cylinder expands immediately following the cluster of right-propagating sparse waves,and the expansion and deformation of the cylinder wall will interfere with the right-and left-propagating sparse waves.Therefore,Eqs.(17)and(20)are unreasonable for describing the sound velocityc1t1and particle velocityu1t1in the detonation products that are on the inner surface of the cylinder att1.As such,on the inner surface of the cylinder,c1t1andu1t1should be the sound velocity and particle velocity when the detonation products interact with the cylinder wall.

4.Cylinder wall velocity v before t1

In the quasi-isentropic model of these experiments,the Tresca yield condition is taken for cylinder expansion:Therefore,according to Newton"s second law,

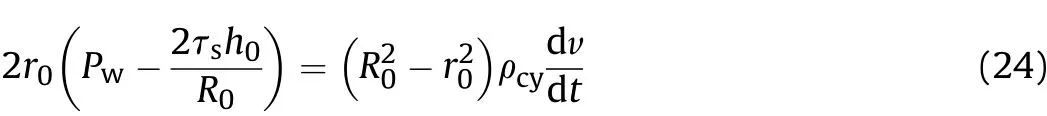
where:r0is the initial inner diameter of the cylinder;R0is the initial outer diameter of the cylinder;tis the time;τsis the shear strength of the cylinder;Pwis the detonation product pressure on the inner surface of the cylinder;h0is the initial wall thickness of the cylinder,i.e.,（R0-r0）;ρcyis the density of the cylinder;and v is the expansion speed of the inner surface of the cylinder in thex/D-t1stage at positionx.

According to the isentropic sound velocity[Eq.(11-a)]and isentropic formula[Eq.(11-b)],can be obtained.At the same time,with the CJ parameters of the detonation wave front,Eq.(24)is transformed into

wherecwis the sound velocity in the detonation products that are on the inner surface of the cylinder,and ρ0is the initial density of the aluminized explosives.The right-propagating waves propagate at the velocityu+c,and the velocityu+cof each wave along the characteristic line remains constant.When the waves propagate to the inner surface of the cylinder,they will be reflected.In this instant,the particle velocity of the detonation products will immediately decrease fromuto the particle velocityuwof the products that are on the inner surface of the cylinder,and the sound velocitycin the detonation products will immediately change to the sound velocitycwin the products that are on the inner surface,thus

Therefore,the derivative of Eq.(26)can be calculated as

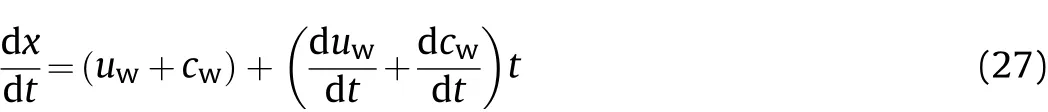
Since the detonation products cling to the inner wall of the cylinder,and this is substituted into Eq.(27)to give

Substituting Eq.(25)into the above equation,the solution is

According to the boundary conditions t=0,andcw=D,the constant β1can be obtained as

Substituting β1into Eq.(29)can obtain the equation forcw,

and the solution of this equation is

where

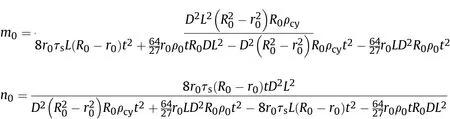
By substituting Eq.(32)into Eq.(25)and integrating,the relationship between the expansion speed of the inner surface of the cylinder and the time before the reaction of Al powder with detonation products can be obtained thus:

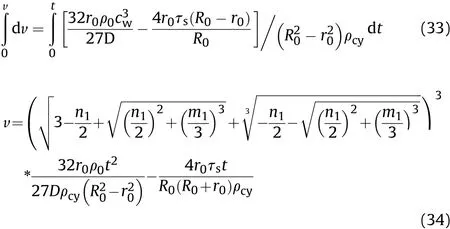
where

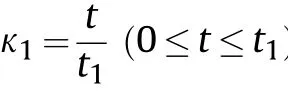
Substitutingt=t1into Eqs.(32)and(34),the calculatedcwand v values are the sound velocityc1t1and particle velocityu1t1,respectively,in the detonation products that are on the inner surface of the cylinder before the reaction of the Al powder with detonation products att1.

Before the Al oxidation reaction occurs,the relationship between the expansion speed of the inner surface of the cylinder and time can be obtained from Eq.(34).The inner diameter of the cylinder can then be solved iteratively using

wheret1is the time at which the reaction between the Al powder and the detonation products is assumed to start,andr1is the inner diameter of the cylinder at positionxatt1.According to the calculation results,the relative specific volume of the detonation products att1can be calculated using υ=r12/r02.

According to the assumption of the quasi-isentropic model that“the material of the cylinder wall is incompressible,and the volume of the wall material remains constant during the cylinder expansion,”the relationship between the inner and outer diameters of the cylinder can be obtained as

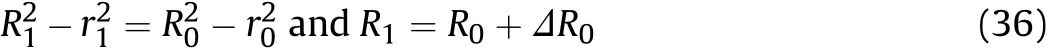
Eq.(35)is then substituted into Eq.(36)to obtain the outer diameter at positionxatt1:

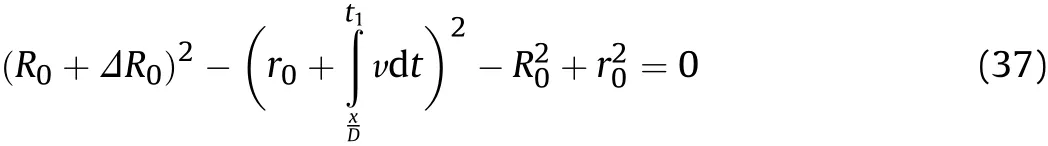
whereR1is the outer diameter of the cylinder at positionxatt1and ΔR0is the variation of the outer diameter of the cylinder at positionxin thex/D-t1stage.The value ofΔR0is calculated using Eq.(37),andR0andr0are updated toR1andr1.

5.Cylinder wall velocity v after t1

5.1.t1-t2 stage

According to the isentropic sound velocity[Eq.(11-a)]and the isentropic formula[Eq.(11-b)],in the 0-t1stageand therefore

According to the quasi-isentropic hypothesis described in Sec.II and the derived proportional relationships in Eqs.(8)-(10),in thet1-t2stage,

where:c1t1andc2t1are the sound velocities in the detonation products on the inner surface of the cylinder before and after the Al oxidation reaction att1,respectively;A1andA2are coefficients related to entropy and the reaction degree of Al in the 0-t1andt1-t2stages,respectively,which represent effective factors for the influence of the Al oxidation reaction on the physical parameters in these two stages;P1t1andP2t1are the pressures of the detonation products on the inner surface of the cylinder before and after the Al oxidation reaction att1,respectively;ρ1t1and ρ2t1are the densities of the detonation products on the inner surface of the cylinder before and after the Al oxidation reaction att1,respectively;T1t1andT2t1are the temperatures of the detonation products on the inner surface of the cylinder before and after the Al oxidation reaction att1,respectively;andu1t1andu2t1are the particle velocities of the detonation products on the inner surface of the cylinder before and after the Al oxidation reaction att1,respectively.

By the isentropic sound velocity[Eq.(11-a)]and isentropic formula[Eq.(11-b)],in isentropic fluids we can obtain

wherePwis the pressure of the detonation products that are on theinner surface of the cylinder during isentropic flow in thet1-t2stage,andcwis the sound velocity in the detonation products that are on the inner surface of the cylinder during isentropic flow in thet1-t2stage.Eqs.(38)and(24)are substituted into Eq.(40),andPwis calculated as

In the secondary reaction stage after detonation,the Tresca yield condition is still adopted for cylinder expansion,so based on Newton"s second law we can obtain

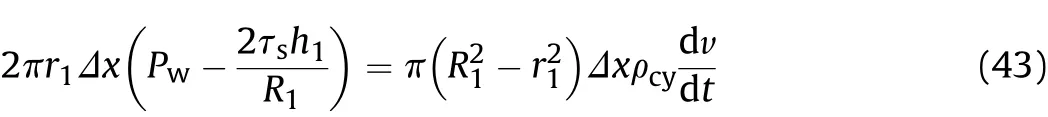
Substituting Eq.(42)into Eq.(43),we calculate the expansion speed of the inner surface of the cylinder with time as

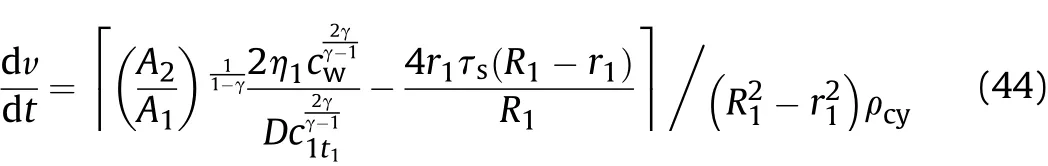
where:

h1is the initial wall thickness of the cylinder in thet1-t2stage,that is,（R1-r1）;and v is the expansion speed of the inner surface of the cylinder in thet1-t2stage at positionx.

The right-propagating waves propagate at velocityu+c,and when the waves propagate to the inner surface of the cylinder,they will be reflected.In this instant,the particle velocity of the detonation products will immediately decrease fromuto the particle velocityuwof the products that are on the inner surface of the cylinder,and the sound velocitycin the detonation products will immediately change to the sound velocitycwin the products that are on the inner surface,as shown in Eq.(26).

The derivative of Eq.(26)can be obtained as shown in Eq.(27),and the movement speed of the product particles on the inner surface is equal to the expansion speed of the inner wall of the cylinder,Therefore,Eq.(27)is simplified as shown in Eq.(28),and substituting Eq.(44)into Eq.(28)and solving it,we obtain

Whent=t1,we have the initial conditions

Substituting these into Eq.(45),we can calculate β2as

After the constant β2is obtained,according to Eq.(45),the sound velocitycwin the detonation products that are on the inner surface of the cylinder during isentropic flow in thet1-t2stage can be obtained from

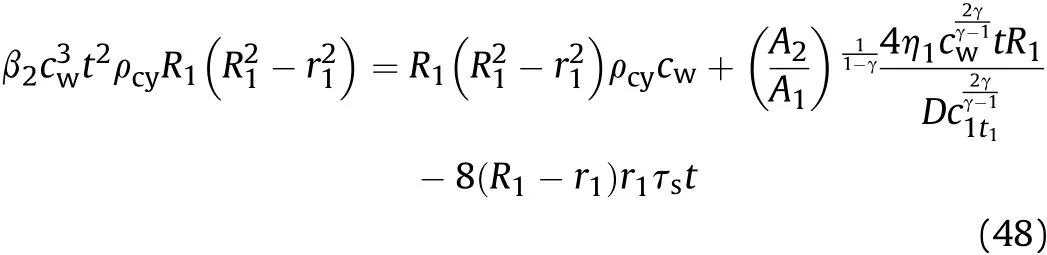
and the influence factor of Al reaction on γ of aluminized explosives is extracted and equal to α,so γ is still equal to the isentropic index of ideal explosives aftert1,the solution of Eq.(48)is as follows:

where

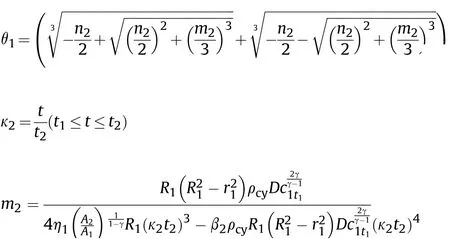
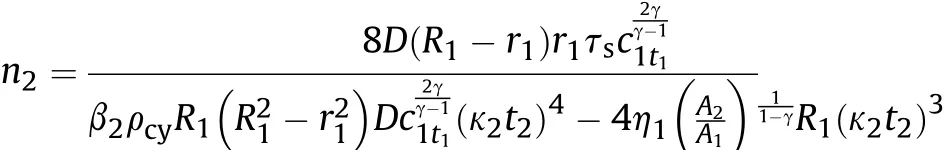
By substituting Eq.(49)into Eq.(44)and integrating,the relationship between the expansion speed of the inner surface of the cylinder and time during isentropic flow in thet1-t2stage can be obtained:

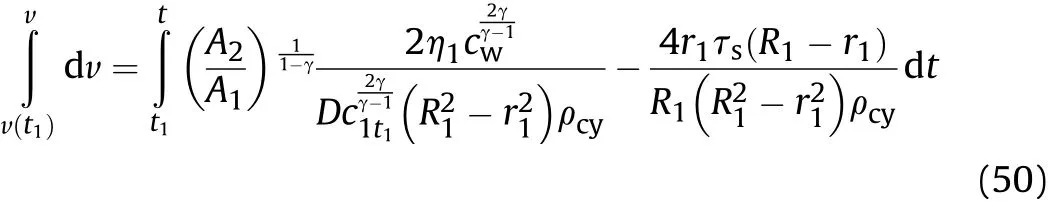
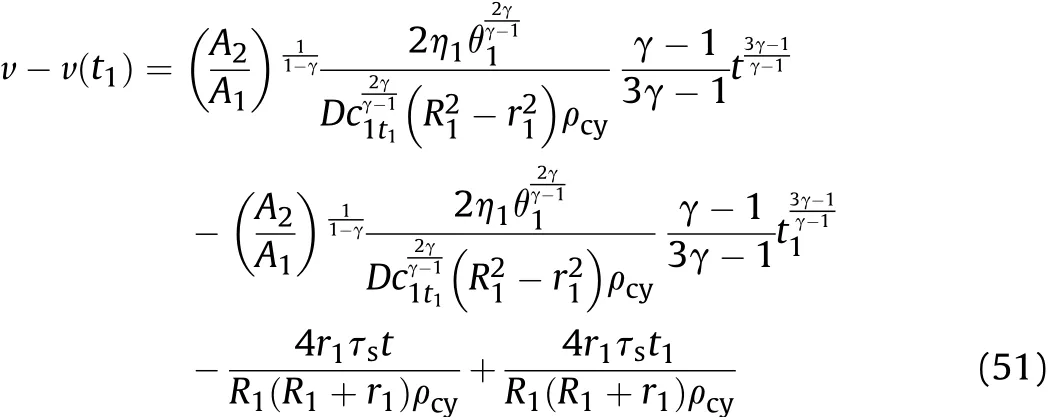
where,v（t1）is obtained by substitutingt=t1into Eq.(34).Substitutingt=t2into Eqs.(49)-(51),the calculatedcwand v are,respectively,the sound velocitycmt1(orc1t2)and particle velocityumt1(oru1t2)in the detonation products that are on the inner surface of the cylinder att2of thet1-t2stage after the reaction products have undergone isentropic expansion.

In thet1-t2stage,the relationship between the expansion speed of the cylinder inner diameter and time is obtained by Eq.(51),and the inner diameter is updated by

wherer2is the inner diameter of the cylinder at positionxatt2,and the relative specific volume of the detonation products att2can be calculated using υ=r22/r12.

According to the assumption of the quasi-isentropic model that“the material of the cylinder wall is incompressible,and the volume of the wall material remains constant during cylinder expansion,”the relationship between the inner and outer diameters of the cylinder can be obtained as

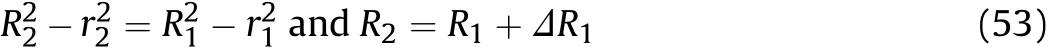
Eq.(52)is substituted into Eq.(53)to obtain the outer diameter at positionxatt2such that

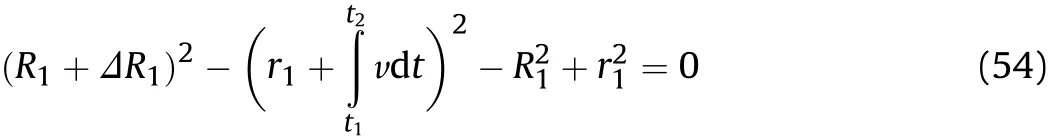
whereR2is the outer diameter of the cylinder at positionxatt2;ΔR1is the variation of the outer diameter at positionxfromt1tot2.The value ofΔR1is calculated from Eq.(54),and thenR1andr1are updated toR2andr2.

5.2.ti-ti+1 stage

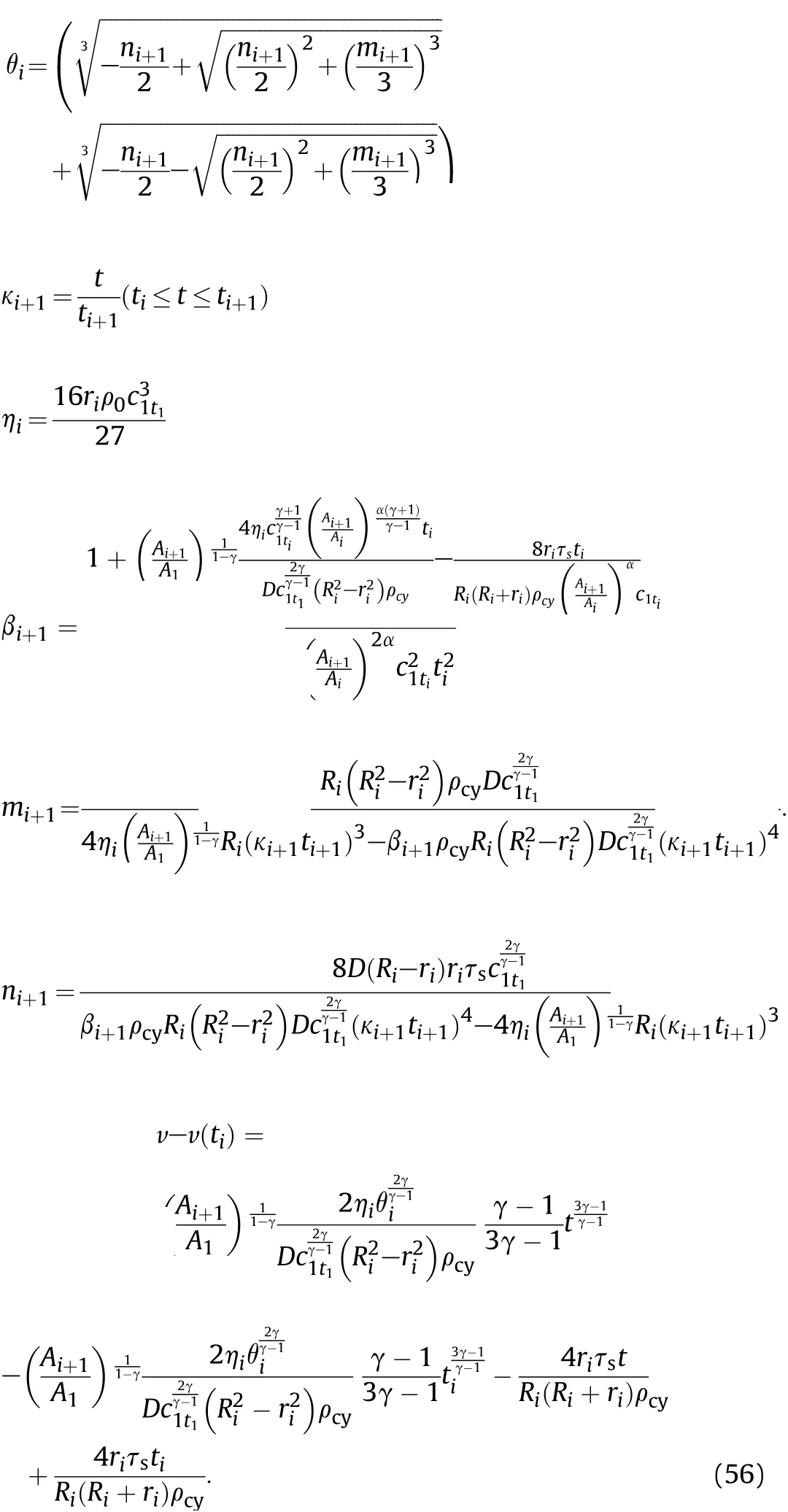
The above deduction process is now generalized.The sound velocitycwin the detonation products that are on the inner surface of the cylinder and the expansion speed of the inner wall of the cylinder during isentropic flow in theti-ti+1stage can be obtained as

where

Substitutingt=ti+1into Eqs.(55)-(56),the obtainedcwand v are,respectively,the sound velocitycmti(orc1ti+1)and particle velocityumti(oru1ti+1)in the detonation products that are on the inner surface of the cylinder atti+1of theti-ti+1stage after the reaction products have undergone isentropic expansion.

6.Physical parameter analysis in zone III

Firstly,it is necessary to determine which area(Zone III or IV)in Fig.5 the calculated positionxof the cylinder is located in atti.Whenti=t1,ifxexceedsE1(E1=L-0.5D（t1-L/D）),thenxis located in Zone III as shown in Fig.6;conversely,xis located in Zone IV as shown in Fig.6.Whenti≥t2,ifxexceedsEi(Ei=Ei-1-UiandFi（u+c）are calculated according to Eq.(81)in Sec.VII.A.),thenxis located in Zone III;conversely,xis located in Zone IV.

6.1.Cylinder inner surface

In this section,the physical parameters of the detonation products that are on the inner surface of the cylinder of Zone III as shown in Fig.6 are studied.As shown in Fig.5,In theti-ti+1stage of Zone III,the right-propagating sparse waves reach the right end of the detonation products(L+Zi)atti,and there will be a cluster of new left-propagating sparse waves propagating into the detonation products,the characteristic equation of these sparse waves is

since there is already a cluster of right-propagating sparse waves in the incoming area of the left-propagating sparse waves in Zone IIIi,there is composite wave flow composed of these two clusters of waves from opposite directions.This can be described by

whereQi+1（x）andPi+1（x）are the deviation caused by the Al reaction atti;Fi+1（u-c）is the deviation caused by the initial condition(L+Zi)of the left-propagating waves atti.In thet1-t2stage,substituting the initial condition(t=t1)into Eq.(58),we get based on Eq.(8),ρmt1can be obtained from

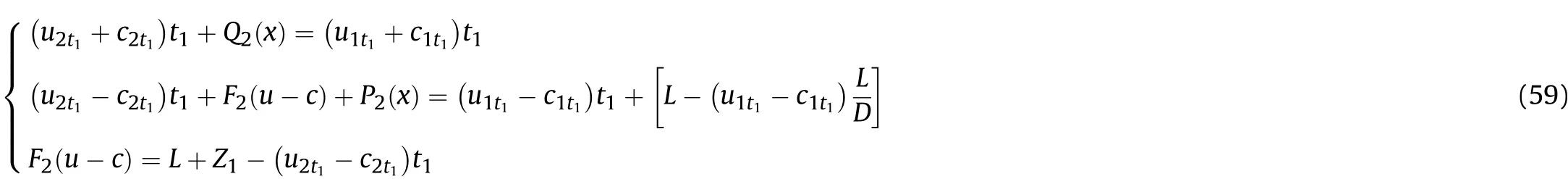
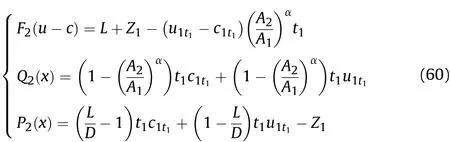
According to the sound velocity and particle velocity in the detonation products that are on the inner surface of the cylinder before the Al powder reacts with the detonation products(Sec.IV),whent=t1in Eqs.(32)and(34),cwand v are equal toc1t1andu1t1,respectively.In thet1-t2stage of Zone III,when the Al oxidation reaction is complete att1,on the inner surface of the cylinder,the particle velocity of the reaction products changes fromu1t1tou2t1,and the sound velocity in the reaction products changes fromc1t1toc2t1.

According to the values ofQ2（x）,F2（u-c）andP2（x）derived from the above equations,the particle velocityu2t1and sound velocityc2t1att1of thet1-t2stage is

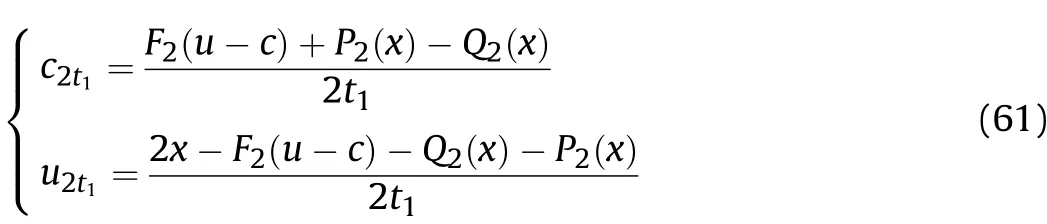
The density ρ1t1of the detonation products that are on the inner surface of the cylinder before the Al oxidation reaction occurring att1of thet1-t2stage is

In thet1-t2stage,whent=t1in Eqs.(49)and(51),cwand v are equal tocmt1(orc1t2)andumt1(oru1t2),respectively.According to the isentropic equation and the isentropic sound-velocity equation,the density of the detonation products satisfiesand

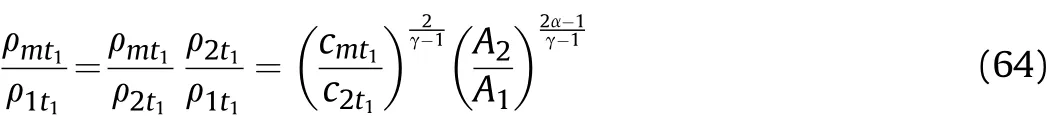
The pressureP1t1of the detonation products that are on the inner surface of the cylinder before the Al oxidation reaction occurring att1of thet1-t2stage is

In thet1-t2stage,according to the isentropic equation and the isentropic sound-velocity equation,the pressure of the detonation products satisfiesand,based on Eq.(8),Pmt1can be obtained as

For the reaction products on the inner surface of the cylinder,the density ρmt1,pressurePmt1,and temperatureTmt1att2of thet1-t2stage after the Al oxidation reaction and isentropic flow can be obtained from the above equations.According to Eqs.(60)and(61),the particle velocityu2t1and sound velocityc2t1in the reaction products att1of thet1-t2stage following the Al oxidation reaction are obtained.The particle velocityumt1and sound velocitycmt1in the reaction products att2of thet1-t2stage after the Al oxidation reaction and isentropic flow are equal to v andcw,as calculated by substitutingt=t2into Eqs.(55)and(56),respectively,wherec1t1is equal to thecwvalue obtained by substitutingt=t1into Eq.(32).Thus,we have

Based on the above derivation,wheni≥2 for the reaction products on the inner surface of the cylinder,the density ρmti,pressurePmti,and temperatureTmtiatti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are obtained as shown in Eq.(72);according to the derived value ofFi（u-c）,Qi（x）andPi（x）,the particle velocityu2ti,and the sound velocityc2tiin the reaction products attiof theti-ti+1stage following the Al oxidation reaction are obtained as shown in Eq.(72);and the particle velocityumtiand sound velocitycmtiin the reaction products atti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are equal tocwand v as calculated by substitutingt=ti+1into Eqs.(55)and(56),respectively,wherec1ti-1andu1ti-1are equal to v andcwobtained by substitutingt=ti-1into Eqs.(55)and(56),respectively;the movement distance of the right end of the detonation productsZiattiis obtained as shown in Eq.(75).

6.2.Away from the inner surface of the cylinder

In this section,the physical parameters of the detonation products that are away from the inner surface of the cylinder in Zone III as shown in Fig.6 are studied.Equation(58)can be used to describe the composite wave flow composed of the two clusters of waves moving in opposite directions.In thet1-t2stage,according to the initial conditiont=t1,Eq.(58)are changed to those in Eq.(59).Based onandP2（x）can be obtained as shown in Eq.(60).

According to the characteristic line analysis of Zone I and Zone II in Sec.III,whent=t1in Eq.(20),canduare equal to the sound velocityc1t1and particle velocityu1t1in the reaction products that are away from the inner surface of the cylinder att1of thet1-t2stage before the Al oxidation reaction,respectively,as shown in Eq.(73).

Substituting the abovec1t1andu1t1into Eq.(60)to calculateQ2（x）,F2（u-c）andP2（x）,in thet1-t2stage of Zone III1,according to the above-derivedQ2（x）,F2（u-c）andP2（x）values,the particle velocity and sound velocity in the reaction products that are away from the inner surface of the cylinder after the Al oxidation reaction are calculated as shown in Eq.(74);whent=t1,c2andu2are equal to the sound velocityc2t1and particle velocityu2t1att1of thet1-t2stage following the Al oxidation reaction,respectively;whent=t2,c2andu2are equal to the sound velocitycmt1and particle velocityumt1att2of thet1-t2stage after the Al oxidation reaction and isentropic flow,respectively,so we have

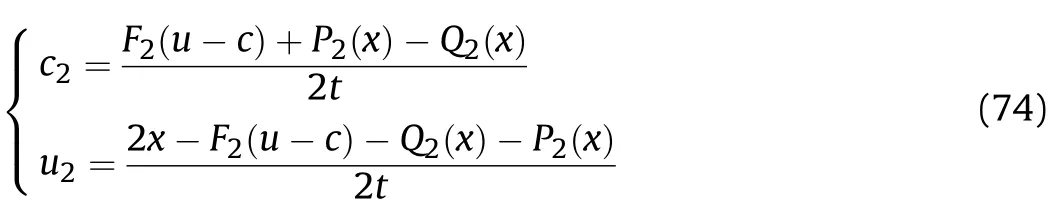
Wheni≥2,according to the derivedZi,Fi（u-c）,Qi（x）andPi（x）values,the particle velocity and sound velocity in the reaction products that are away from the inner surface of the cylinder after the Al oxidation reaction of theti-1-tistage are calculated as shown in Eq.(75).Whent=ti-1,cianduiare equal to the sound velocityc2ti-1and particle velocityu2ti-1atti-1of theti-1-tistage following the Al oxidation reaction,respectively.Whent=ti,cianduiare equal to the sound velocitycmti-1and particle velocityumti-1attiof theti-1-tistage after the Al oxidation reaction and isentropic flow,respectively.The density ρmti,pressurePmti,and temperatureTmtiof the reaction products that are away from the inner surface of the cylinder atti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are the same as those shown in Eq.(72),but the parameters(cmticmti-1,cmt1)related to the sound velocity in the equations need to be obtained using Eqs.(75)and(73):

7.Physical parameter analysis in zone IV

7.1.Cylinder inner surface

In this section,the physical parameters of the detonation products that are on the inner surface of the cylinder of Zone IV as shown in Fig.6 are studied.As shown in Fig.5,there is a cluster of left-propagating sparse waves in Zone IV within the length of the cylinder(0-L),which can be described by

whereFi（u+c）is the deviation caused by the Al oxidation reaction.In thet1-t2stage,according to Eq.(8),the relationships

can be derived.Based on the sound velocity and particle velocity in the detonation products that are on the inner surface of the cylinder before the Al powder reacts with the detonation products(Sec.IV),whent=t1in Eqs.(32)and(34),cwand v are equivalent to the sound velocityc1t1and particle velocityu1t1on the inner surface of the cylinder att1before the Al oxidation reaction,respectively.

In thet1-t2stage,the initial conditiont=t1is substituted into Eq.(76),and thenU2andF2（u+c）can be calculated according to Eqs.(76)and(77)such that

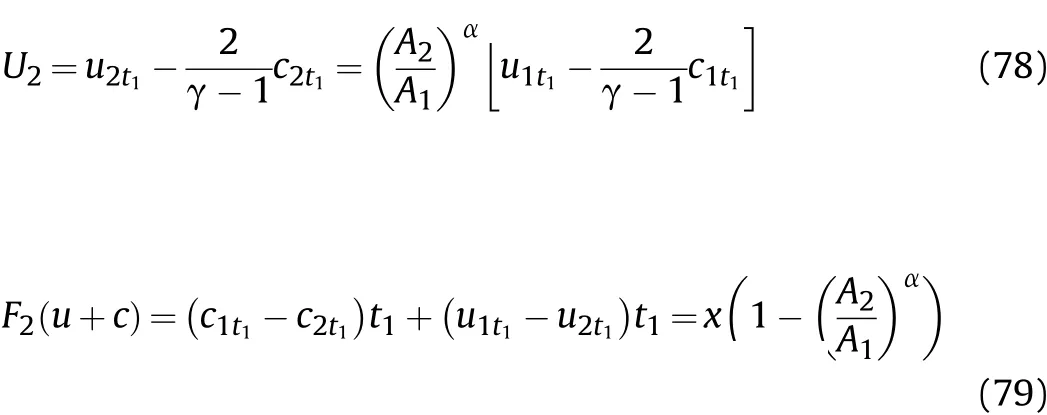
In thet1-t2stage of Zone IV,for the reaction products on the inner surface of the cylinder,according to Eqs.(76),(78),and(79),the particle velocityu2t1and sound velocityc2t1in the reaction products att1of thet1-t2stage after the Al oxidation reaction are calculated as shown in Eq.(80);the particle velocityumt1and sound velocitycmt1in the reaction products att2of thet1-t2stage after the Al oxidation reaction and isentropic flow are equal tocwand v as calculated by substitutingt=t2into Eqs.(55)and(56),respectively;the density ρmt1,pressurePmt1,and temperatureTmt1att2of thet1-t2stage after the Al oxidation reaction and isentropic flow are obtained based on the derivation method in Sec.VI.Thus,we have

Wheni≥2,for the reaction products on the inner surface of the cylinder,the density ρmti,pressurePmti,and temperatureTmtiatti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are obtained as shown in Eq.(81);according to Eq.(76),Fi（u+c）andUi,the particle velocityu2ti,and sound velocityc2tiin the reaction products attiof theti-ti+1stage after the Al oxidation reaction are obtained as shown in Eq.(81);the particle velocityumtiand sound velocitycmtiin the reaction products atti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are equal tocwand v as calculated by substitutingt=ti+1into Eqs.(55)and(56),respectively.

7.2.Away from the inner surface of the cylinder

In this section,the physical parameters of the detonation products that are away from the inner surface of the cylinder of Zone IV as shown in Fig.6 are studied.Eq.(76)can also be used to describe the cluster of left-propagating sparse waves.In thet1-t2stage,according to Eq.(8),there are relationships as shown in Eq.(77).Based the characteristic line analysis of Zone I and Zone II in Sec.III,whent=t1in Eq.(17),canduare equal to the sound velocityc1t1and particle velocityu1t1away from the inner surface of the cylinder att1before the Al oxidation reaction,respectively,so that

Substitutingc1t1andu1t1into Eqs.(76)-(77)calculatesU2andF2（u+c）:

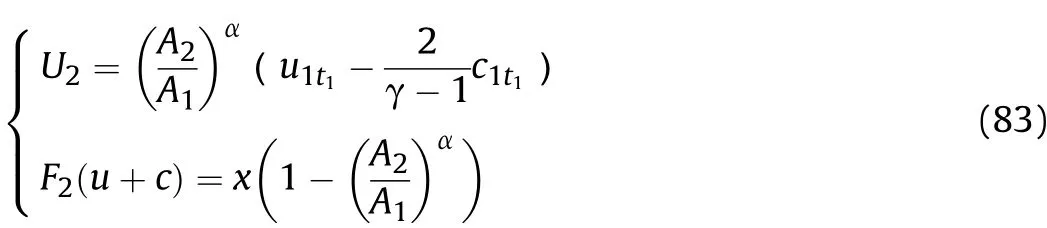
In thet1-t2stage of Zone IV,according to Eqs.(76)and(83),the particle velocity and sound velocity in the reaction products that are away from the inner surface of the cylinder after the Al oxidation reaction are calculated as

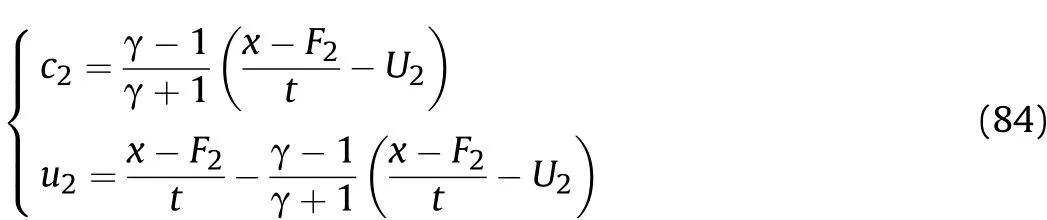
Whent=t1,c2andu2are equal to the sound velocityc2t1and particle velocityu2t1att1of thet1-t2stage after the Al oxidation reaction,respectively;whent=t2,c2andu2are equal to the sound velocitycmt1and particle velocityumt1att2of thet1-t2stage after the Al oxidation reaction and isentropic flow,respectively.

Wheni≥2,according to the derived values ofFi（u+c）andUi,the particle velocity and sound velocity in the reaction products that are away from the inner surface of the cylinder after the Al oxidation reaction of theti-1-tistage are calculated as shown in Eq.(85);whent=ti-1,cianduiare equal to the sound velocityc2ti-1and particle velocityu2ti-1atti-1of theti-1-tistage after the Al oxidation reaction,respectively;whent=ti,cianduiare equal to the sound velocitycmti-1and particle velocityumti-1attiof theti-1-tistage after the Al oxidation reaction and isentropic flow,respectively;the density ρmti,pressurePmti,and temperatureTmtiof the reaction products that are away from the inner surface of the cylinder atti+1of theti-ti+1stage after the Al oxidation reaction and isentropic flow are the same as those shown in Eq.(81),but the parameters(cmticmti-1,cmt1)related to the sound velocity in the equations need to be obtained using Eqs.(85)and(82):

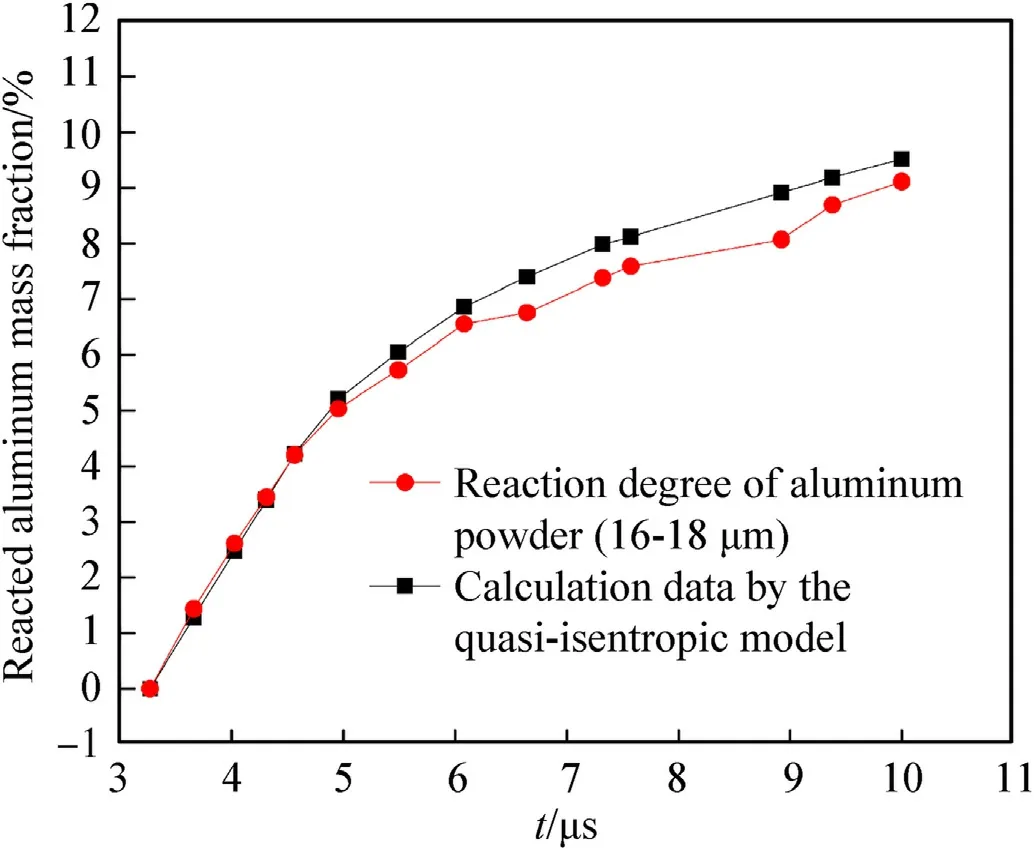
Fig.7.Reaction degree of the Al powder(16.0-18.0 μm)as a function of time.

Fig.8.Reaction degree of the Al powder(200.0 nm)as a function of time.

Fig.9.Change in the cylinder outer diameter R for Al powder(16.0-18.0 μm)as a function of time.

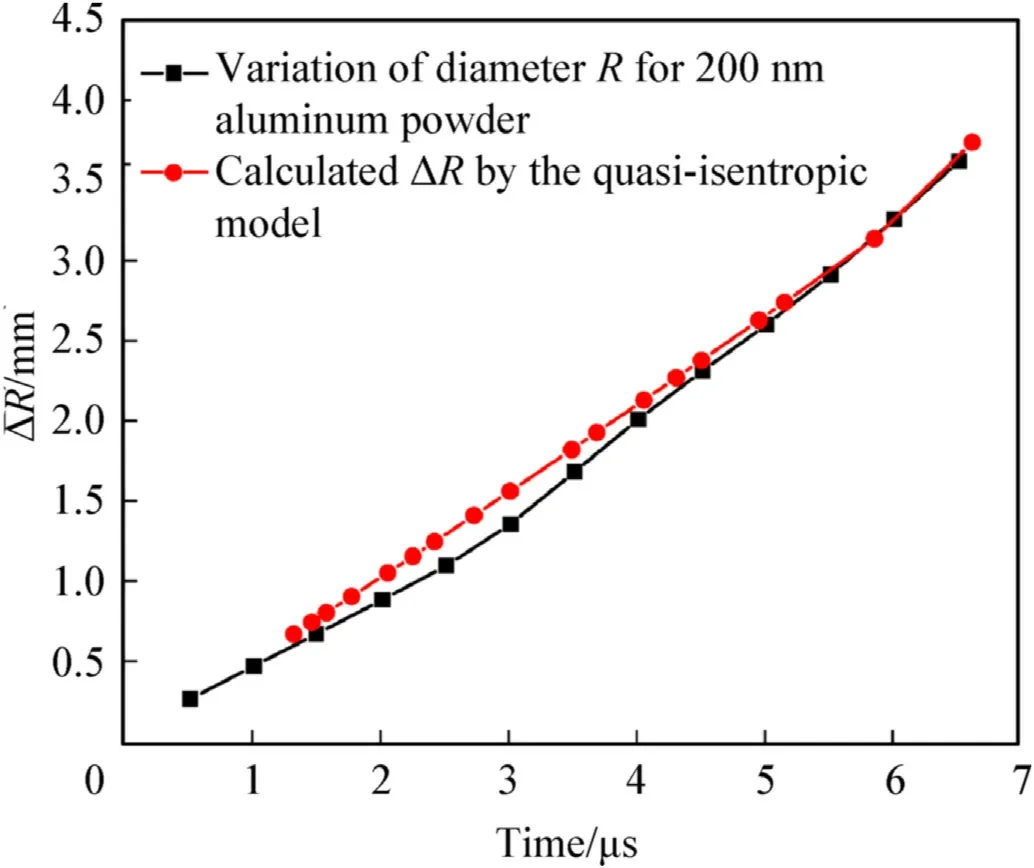
Fig.10.Change in the cylinder outer diameter R for Al powder(200.0 nm)as a function of time.

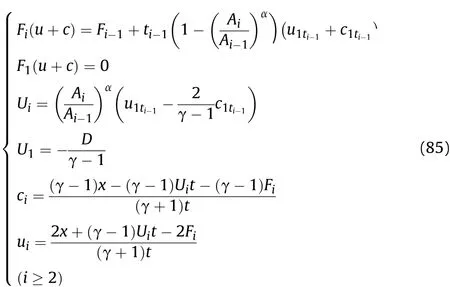
8.Analysis of calculation results

8.1.Verification of the quasi-isentropic model

The quasi-isentropic model for cylinder experiments with aluminized explosives was verified and analyzed using the experimental data from two kinds of aluminized explosives presented in Ref.24.The physical parameters of aluminized hexanitrohexaazaisowurtzitane(CL-20)are shown in Table 1[24,27].The physical parameters and charge size of the cylinder are shown in Table 2[24].

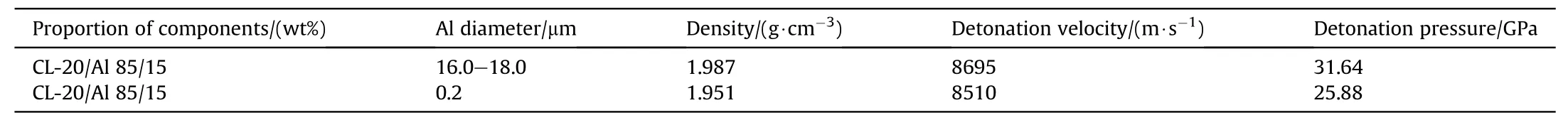
Table 1Physical properties of the aluminized CL-20 explosives[24,27].

Table 2Physical properties and charge size of the cylinder[24].

In this paper,using the parameters in Tables 1 and 2 and the Al reaction degree shown by the red lines in Figs.7 and 8 from the experimental data of Ref.24,the expansion law of the cylinder outer wall at a position 15.0 mm away from the initiation surface with time is calculated by the quasi-isentropic model proposed,as shown by the red lines in Figs.9 and 10.

In Ref.24,the parameters of the JWL EOS of the detonation products for the aluminized CL-20 explosives were fitted using the experimental data,as shown in Table 3,the main purpose of cylinder experiments was to analyze the workability of the detonation products,and descriptions of the detonation products were considered mainly in simulations;the initiation and growth processes of the explosion were not the focus of the study.In the present study,based on the parameters in Tables 1-3,these cylinder experiments with aluminized explosives are simulated in LS-DYNA,the top of the aluminized explosives is taken as initiation surface to load the explosives instead of a detonator and explosive lens,the expansion law of the cylinder outer diameter is obtained,as shown by the black lines in Figs.9 and 10.

From the parameters in Tables 1 and 2 and the expansion law of the cylinder outer diameter shown by the black lines in Figs.9 and 10,the reaction degree of the Al powder as a function of time was calculated by the quasi-isentropic model proposed,as shown by the black lines in Figs.7 and 8.

Table 3Parameters of the JWL EOS of the detonation products for the aluminized CL-20 explosives[24].

Table 4Physical properties of the aluminized RDX explosives[29,30].

Table 5Physical properties and charge size of the cylinder[29].

In the above calculations,becausetiis substituted into the calculation of βi,andtiis the time from the initiation at the initiation surface of the explosives,the time parameter used to solvecwis absolute time;that is,the timekeeping starts from the time when the aluminized explosives are initiated;when the detonation wave propagates to the calculated position,the cylinder wall of the x position begins to expand,so the time parameters used to solvevandrare relative time;that is,the timekeeping starts from the time when the cylinder wall at this position begins to move.

Comparisons between the calculation results obtained using the quasi-isentropic model and the factual data are shown in Figs.7-10.It can be seen that the reaction degree of the Al powder calculated according to the cylinder outer diameter is in good agreement with the experimental results;additionally,the expansion rule of the cylinder wall calculated according to the reaction degree of the Al powder is basically consistent with the real data.The maximum errors in these two parameters are not more than 13.0 %.Therefore,it can be said that the quasi-isentropic model of cylinder expansion with aluminized explosives has good accuracy and applicability;it can be used not only to establish the relationship between the cylinder expansion law and the reaction degree of the Al powder,but also to obtain change rules for the physical parameters of the detonation products during Al oxidation reaction.

It can be observed from Figs.7-10 that the reacted Al mass fraction of the aluminized explosives with 200.0 nm Al powder is greater than that of the aluminized explosives with 16.0-18.0 μm Al powder at the same time,the displacement of the cylinder wall driven by 200.0 nm Al powder is larger,and the reaction rate of 16.0-18.0 μm Al powder increases again from 9.0 μs.Compared with large-size Al powder,small-size Al powder has larger specific surface area and better thermal conductivity,which makes it easier to gasify and react with detonation products,so the reaction rate isfaster in the early stage.However,due to the larger number of small-size Al powder,the heat transfer between Al powder and detonation products is not complete,which leads to the incomplete gasification of Al and affects the reaction completeness.At the same time,the heat from a single large-size Al particle is more than that from a small-size Al particle,which is more conducive to the reaction persistence,and the reaction rate is faster in the later stage.

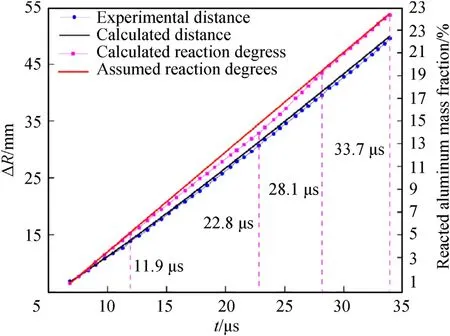
Fig.11.Cylinder outer diameter R and reaction degree of the Al powder as functions of time for aluminized RDX explosives with 15.0 % Al content.

8.2.Application of the quasi-isentropic model

The quantity of oxidizing molecules produced by the RDX detonation reaction is limited for aluminized RDX explosives,so they can only react with a certain proportion of the Al atoms.According to analysis of the detonation products of aluminized RDX explosives,the optimum Al content in RDX explosives is about 30.0%[23].When the Al content is greater than 30.0%,the quantity of alumina in the detonation products does not increase further.The results of 50.0-mm cylinder experiments with RDX explosives and two kinds of aluminized RDX explosives with 15.0%and 30.0%Al content are reported in Ref.[28].The results show that within the time range recorded in the cylinder experiments,the aluminized explosives with 15.0 % Al content had the greatest work capacity.Therefore,it is necessary to examine the relationship between the different reaction mechanisms of Al powder in the detonation products and the work capacity of aluminized RDX explosives with 15.0 % and 30.0 % Al content.

According to the experimental setup of the cylinder experiments in Ref.29,the parameters(the cylinder outside diameter and reaction degree of Al powder)at a position 300.0 mm away from the initiation surface during the cylinder expansion were calculated using the quasi-isentropic model.The calculated results were compared with the experimental results to verify the accuracy of the quasi-isentropic model and to study the influence of the reaction degree and reaction mechanisms of Al powder on the work capacity of the explosives.The physical parameters of the aluminized RDX explosives are shown in Table 4[29,30],and the physical parameters and charge size of the cylinder are shown in Table 5.

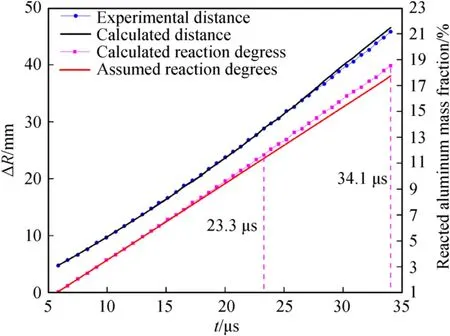
Fig.12.Cylinder outer diameter R and reaction degree of the Al powder as functions of time for aluminized RDX explosives with 30.0 % Al content.

Firstly,the part of the quasi-isentropic model in which the Al powder does not react was calculated and verified for the cylinder experiments.The end surface of the cylinder was selected as the calculation position(i.e.,L=0.5 m),the time parametertwas 6.2×10-5s(t=L/D),and the sound velocitycwfollowing the detonation front in the detonation products of the aluminized explosives with 15.0 % and 30.0 % Al content were calculated as 8115.5 m s-1and 7628.8 m s-1,respectively.According touw+cw≈Danduw≈0 when following the detonation front,this sound velocitycwand detonation velocityDare approximately equal.According to Table 4,the detonation speedsDof the two aluminized explosives were 8121.0 m/s and 7879.0 m/s,respectively.It can therefore be said that the part of the quasi-isentropic model in which the Al powder does not react is accurate.

The part of the quasi-isentropic model in which the Al powder reacts with the detonation products was then used for calculation and analysis.It is assumed that the Al oxidation reaction takes place at a constant reaction rate,so the reaction degree of the Al powder in each time interval can be obtained according to

where:tiandti+1are the starting and ending times of the calculated time interval,andTinandTfiare the starting time of Al oxidation reaction and the end of the recording time of the cylinder experiments,respectively,with these four time parameters being recorded from the initiation of the explosives;and λtotalis the total reaction degree of the Al powder betweenTinandTfi.

When the volume of the detonation products in the cylinder expands to about 1.24 times the initial volume,the Al powder in the aluminized explosives with 2.0-50.0 μm Al constituents begins to react with the detonation products[24].Therefore,when the Al content is 15.0 % or 30.0 %,it is assumed that the Al oxidation reaction occurs at 3.6 μs or 4.0 μs,respectively,according to the cylinder outer diameters recorded in the experiments.From the cylinder outer diameters recorded in the experimental data at 3.6 μs and 4.0 μs,and using the quasi-isentropic model,for aluminized RDX explosives with 15.0 % and 30.0 % Al content,the reaction degrees of the Al powder were calculated as 24.5 % and 17.7 % at 33.9 μs and 34.0 μs,and these were taken as the assumed Al reaction degrees with 15.0 % and 30.0 % Al,respectively.

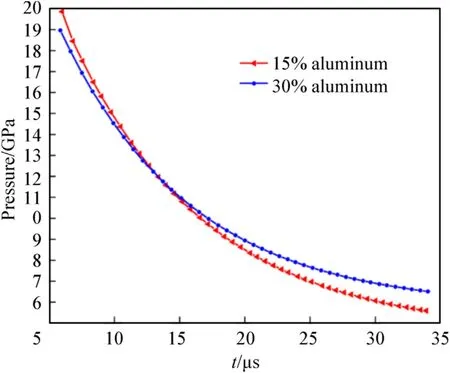
Fig.13.Pressure of the detonation products as a function of time for aluminized RDX explosives with 30.0 % and 15.0 % Al.

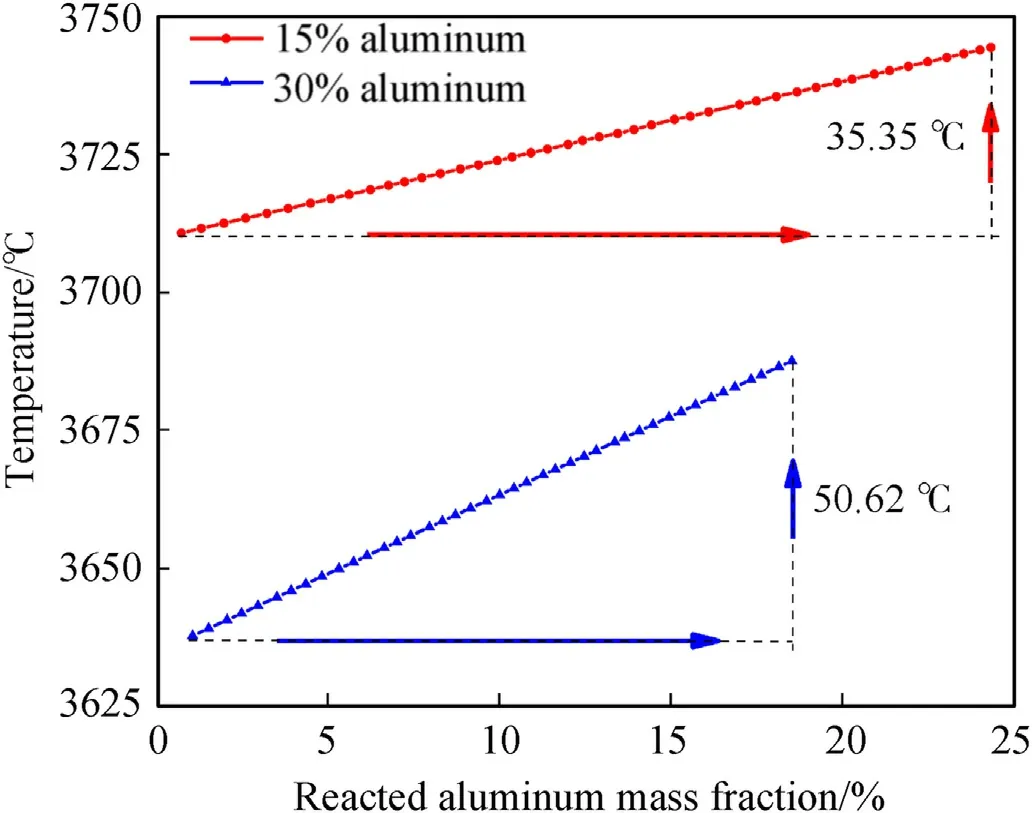
Fig.14.Temperature of the detonation products as a function of the reaction degree of the Al powder for aluminized RDX explosives with 30.0 % and 15.0 % Al.

Assuming that the reaction rates of the Al powder are constants,the assumed reaction degree of the Al powder in each time interval can be obtained according to Eq.(86).The reaction degree of the Al powder can also be calculated using the quasi-isentropic model from the cylinder outer diameter recorded in the experiments.Based on the quasi-isentropic model,the assumed reaction degree,calculated reaction degree,and the cylinder wall movement rules calculated from the calculated reaction degree are shown in Fig.11 and Fig.12.From these figures,it can be seen that the variation trends in the calculated distances obtained from the calculated reaction degrees of the Al powder and the experimental distances recorded by experimentsΔRare similar to the reaction degrees of the Al powder calculated from the cylinder outer diameterRin the experimental data.The above analysis shows that the Al powder reacts at non-constant rates within the time ranges recorded in the cylinder experiments;the degree and rate of the reaction of the Al powder have significant effects on cylinder expansion in the secondary reaction zone after detonation.Compared with the assumed Al reaction degree calculated from the initial and final cylinder states of the time range recorded in the cylinder experiments,the Al reaction degree calculated by dividing the whole time range into multiple small intervals is slightly different at the end of the experimental recording time.For the aluminized RDX explosives with 15.0 % and 30.0 % Al content,the assumed Al reaction degrees were 24.5 % and 17.7 %,respectively,while the calculated Al reaction degrees were 24.3%and 18.5%,respectively.Therefore,when the quasi-isentropic model is used for derivation and calculation,the calculation accuracy can be improved by subdividing the time intervals as much as possible.

The following can be observed from Figs.11 and 12.Compared with the assumed Al reaction degree,for aluminized RDX explosives with 15.0 % Al content,in the initial 6.8 μs-11.9 μs stage,the calculated Al reaction degree coincides with the assumed one,and the Al oxidation reaction takes place at a constant reaction rate.In the subsequent 11.9 μs-22.8 μs stage,the calculated Al reaction rate decreased with time,and the reaction degree gradually became lower than the assumed one.However,the calculated Al reaction rate from 22.8 μs gradually increased and exceeded the assumed constant reaction rate,until at 28.1 μs,the calculated Al reaction degree became approximately equal to the assumed one.For the aluminized RDX explosives with 30.0%Al content,in the initial 5.9 μs-23.3 μs stage,the calculated reaction rate and degree of the Al powder are basically equal to the assumed values,and the reaction rate is basically constant.The calculated Al reaction rate increased gradually from 23.3 μs,resulting in the final differences between the calculated and assumed reaction degrees.

Based on the different Al contents(15.0 % and 30.0 %),the reaction between the Al powder and the detonation products can be divided into a diffusion reaction and a kinetic reaction.When the Al content is 15.0 %,the amount of oxidizing gas around the Al particles is enough to maintain a continuous Al oxidation reaction in the detonation products.The oxidizing gas mixes rapidly with Al vapor on the surface of the Al particles,which means that the redox reaction takes place almost on the surface of the Al particles.At this time,the reaction rate of the Al powder is mainly affected by its own redox reaction rate(kinetic reaction);however,the formation of an oxide film on the Al surface will affect the generation of Al vapor and the mixing of this vapor with the oxidizing gas,resulting in a slowdown of the kinetic reaction rate.The consumption of oxidizing gas in the previous stage of the kinetic reaction leads to a decrease in its concentration,so Al vapor reacts with the oxidizing gas at a certain distance from the Al particle surface,and the reaction changes from a kinetic reaction to a diffusion reaction.At the same time,the heat released by Al oxidation reaction melts and breaks the oxide film on the surface of the Al particles that was formed in the previous stage,which speeds up the kinetic reaction rate.The kinetic reaction and the diffusion reaction occur simultaneously,and the rate of the Al combustion reaction increases continuously.

When the Al content is 30.0%,because the quantity of oxidizing gas around the Al particles is not enough to maintain a continuous thermal reaction in the detonation products,the vaporized Al reacts with the oxidizing gas,generating alumina and releasing energy,at a certain distance from the surface of the Al particles.The reaction products diffuse with the expansion of the detonation products,and the reaction rate is controlled by the diffusion rate between the Al vapor and the surrounding oxidizing gas(diffusion reaction).The Al powder does not participate in the detonation reaction or does not react completely before the CJ plane.When the Al content is higher,it dilutes the concentration of the detonation reactants for the reaction kinetics.Additionally,the Al powder absorbs part of the energy released by the detonation in melting and vaporizing the Al particles,which will reduce the energy and work capacity of the detonation reaction zone and the early stage of the secondary reaction zone.When the Al powder fully absorbs heat and evaporates into the detonation products,the surface area of the evaporation reaction will be larger due to the higher Al content.Therefore,when the content of oxidizing gas is sufficient,the diffusion reaction rate of the Al increases continuously,and the energy release in the later stage of the secondary reaction zone is enhanced,which subsequently improves the work ability of the explosives.

The changes in the pressure and temperature of the detonation products as a function of time for aluminized RDX explosives with 30.0 % and 15.0 % Al are shown in Figs.13 and 14,respectively.Compared with the RDX-based aluminized explosive with 30.0%Al,the shock wave overpressure and the pressure closely following the shock wave of the explosive with 15.0 % Al are higher,but the pressure decays more rapidly with time,and the positive pressure becomes lower from 11.5 μs.It can be inferred from this that when the Al content is between 15.0%and 30.0%,the action time of the positive pressure and the work effect of overpressure will be prolonged.The detonation temperature of the above two explosives was about 3600.0-3700.0°C,due to the secondary reaction between the Al powder and the detonation products.The temperature increased slightly after detonation,and rate of increase of the explosive with 30.0 % Al was faster.Moreover,the secondary reaction can keep the temperature of the detonation products above 1500.0°C for tens of microseconds[30].It can be seen that these explosives have the characteristics of a high explosion temperature and a long-duration thermal effect.Al powder generally does not participate in the reaction at the CJ plane,but also absorbs heat to reduce the energy of the wave front used to support detonation propagation.This reduces the detonation pressure and detonation temperature to a certain extent,but prolongs the positive pressure action time,resulting in a continuous increase in temperature after detonation and maintaining the high temperature of the detonation products for a longer period,so the addition of Al powder improves the aftereffect of the explosives.

9.Conclusions

Based on the quasi-isentropic hypothesis,characteristic line analysis,and isentropic theories,a quasi-isentropic model of aluminized explosive driving cylinder has been established in this paper.This model can realize the following calculations.The expansion law of the cylinder wall can be predicted from the reaction degree of the Al powder,and the relationship between the Al reaction degree and time can be calculated from the outer diameter of the cylinder.The relationship between the sound velocityc,particle velocityu,density ρ,pressureP,and temperatureTof the detonation products on the inner surface of the cylinder and away from the inner surface of the cylinder(or Al powder reactivity)can be described as functions of time.

The accuracy and rationality of the quasi-isentropic model were verified using the simulation results for aluminized CL-20 explosives driving a cylinder.In general,the effective acting time in the cylinder experiments is no more than 40.0 μs,but Al powder requires hundreds of microseconds to react completely after explosive detonation.However,the quasi-isentropic model can be used to predict the subsequent variation law of the physical quantities(such as pressurePand temperatureT)of the detonation products with the reaction degree of the Al powder after the cylinder being broken.

When the Al content in the explosives was varied(15.0 % and 30.0 %),the intensity,occurrence time,and duration of the two reaction forms(diffusion and kinetic)of the Al powder and detonation products were different.The variation of the Al reactivity with time is therefore affected by the Al content.Compared with RDX-based aluminized explosives with 30.0 % Al,the shock wave overpressure of explosives with 15.0 % Al are higher,but the pressure decays faster with time,and the positive pressure is lower from 11.5 μs.It can be inferred from the trend in pressure change that when the Al content is between 15.0 % and 30.0 %,the action time of positive pressure and the work effect of overpressure will be prolonged.Due to the secondary reaction between the Al powder and the detonation products,the temperature increases after detonation,and the rate of temperature increase in explosives with 30.0 % Al is faster.

Using reasonable assumptions,the quasi-isentropic model introduces the isentropic theory into aluminized explosives driving a cylinder and establishes relationships between the expansion law of the cylinder,the physical parameters of the detonation products,and the reaction degree of the Al powder.Additionally,when the cylinder is completely broken,the subsequent work capacity of aluminized explosives can also be calculated using this model until the Al powder has reacted completely.The quasi-isentropic model therefore provides a non-empirical theoretical model for evaluating the work performance of different aluminized explosive formulations.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This paper is supported by National Natural Science Foundation of China(Grant No.11872120).