Modified couple stress and thickness-stretching included formulation of a sandwich micro shell subjected to electro-magnetic load resting on elastic foundation
2022-11-28JunSongDidiWuMohammadArefi
Jun Song ,Didi Wu ,Mohammad Arefi
a School of Energy Engineering,Huanghuai University,Zhumadian,463000,Henan,China
b Henan Key Laboratory of Smart Lighting,Huanghuai University,Zhumadian,463000,Henan,China
c School of Culture and Communication,Zhumadian,463000,Henan,China
d Faculty of Mechanical Engineering,Department of Solid Mechanics,University of Kashan,Kashan,87317-51167,Iran
e Department of Engineering and Architecture,University of Parma,Parco Area delle Scienze 181/A,43124,Parma,Italy
Keywords:Electromagnetoelastic bending analysis Curved shell Thickness stretching formulation Modified couple stress theory
ABSTRACT This paper studies electromagnetoelastic static investigation of a sandwich doubly curved microshell subjected to multi-field loading based on a new thickness stretching included refined higher order shear/normal deformable model.Modified-couple-stress-theory(MCST)is used for accounting small-scaledependency.The numerical results are derived using an analytical method.The effect of small scale parameter in micro scale,initial electric and magnetic potentials and foundation parameters is studied on the electromagnetoelastic bending results.It is confirmed an enhancing in stiffness of small scale shell with an increase in micro length scale parameter.
1.Introduction
Plates and shells are the important structures in various industries.Analysis of plates and shells is very important for designer and scientists.This importance is because of their vast applications in various industries and situations such as chemical reactors,weapon instruments and aerospace technologies.Analysis of plate and shells in general state is a three-dimensional analysis.One can conclude that a three-dimensional analysis needs a complicated formulation and a more complicated solution method because of complex boundary conditions.Because of these complexities,researchers used shear deformation theory and a two-dimensional analysis.Although two-dimensional analysis leads to an acceptable output for more plates and shells,however it does not present a valid and accurate solution for thick plates and plates including out of plane boundary conditions.To reach an acceptable solution and formulation,scientist proposed new thickness stretching included formulations[1-4].This paper investigates application of higher order shear/normal deformable model to electro-magnetoelastic analysis of nanoshell.
Sahmani and Aghdam[5]developed a very small scale dependent model using nonlocal strain gradient theory(NSGT)for nonlinear buckling/postbuckling analyses of cylindrical composite nanoshell in electro-magneto-mechanical environment.The proposed size-dependent theory had both stiffening and softening effects,concurrently.After derivation of nonlinear prebuckling deformations,perturbation method was used to derive an explicit relation for buckling load of nanoshell.Arefi[6]used MCST formulation for static bending analysis of a curved microbeam.A shear deformable model was employed.The bending results were expressed in terms of initial electrical and mechanical loads.Shen et al.[7]employed Gibbs-type variational principle for static bending analysis of Kirchhoff microplate made from magnetoelectroelastic materials.Solution of the governing equations has been provided based on Fourier-Bessel series.They concluded that the bending results provided by the present size-dependent theory is smaller than those provided by classical theory.Tan and Chen[8]studied deflection analysis of a multi-layered cantilever microactuator in thermal and mechanical environment based on MCST.They discussed on the structural behavior of micro structure with changes of scale factor.Lu et al.[9]and Wang et al.[10]presented a work on the application of piezoelectric materials in detecting traffic loading.
Akg¨oz and Civalek[11]developed a new higher-order model including strain gradient theory for transient responses of a beam.Effect of material length scale parameter and geometric parameters was studied on the free vibration responses.A hyperbolic theory and modified strain gradient theory(MSGT)was used for static bending and buckling analyses of a beam by Akg¨oz and Civalek[12].Akg¨oz and Civalek[13]employed MCST for buckling analysis of a microbeam in thermal environment.Dastjerdi et al.[14]studied time-dependent bending responses of a spherical nanostructure accounting gyroscopic effect made of FG materials.A software comparison was used for verification the method.Numano˘glu et al.[15]studied FEA of a Timoshenko beam in nano scale.Akg¨oz and Civalek[16]studied static bending response of SWCNTs based on MSGT.Effect of micro length scale parameter and type of nanofillers distribution was studied on the responses.system.Zhang et al.[57]studied effect of foundation as well as electromagnetomechanical fields on the responses of Timoshenko beam.Refs.[58-64]used piezoelectric materials in technical applications.Some details of mathematical methods for solution of linear and nonlinear governing equations are observed in the Refs.[65-77].
The main contribution of this work is size-dependent analysis of the micro doubly curved shell using MCST and quasi three dimensional piezomagnetic elasticity theory.The thickness stretching is accounted in the formulation for more accurate results.The effect of multi-field loading is studied on the sizedependent results in details.
2.Formulations
Modified couple stress formulation is used for analysis of a sandwich micro shell.Based on this theory for electro-magnetic materials,the strain energy is[62-66].
in which σi,τijare normal and shear stresses,εi,γijare normal and
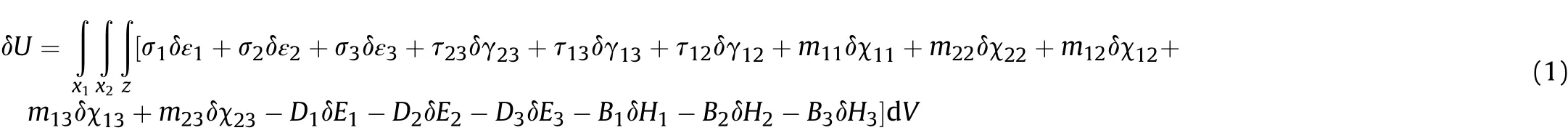
Wave propagation of a nano-tube made of magnetoelectroelastic materials was studied by Ebrahimi et al.[17].They discussed on the impact of mode number,small scale parameter and multi-field loadings on the responses.Hong et al.[18]used an extended MCST for static and dynamic analyses of a microbeam composed of two-phase material based on variational formulation.Soni et al.[19]employed classical plate theory for transverse transient analysis of thin plate made of piezoelectric/piezomagnetic materials including a crack reinforced with nanofibers.Forced vibration responses have been analyzed using perturbation method.The effect of surrounded environment has been simulated using a fluid with velocity.Farajpour et al.[20]studied nonlinear buckling analysis of a hybrid nanoshell subjected to thermal environment reinforced with carbon nanotubes and microtubule based on nonlocal elasticity theory.Derivation of buckling loads has been performed using Galerkin’s approach.Buckling analysis of a magneto-electro-elastic nano-plate was studied by Park and Han[21]based on a new HOSDT and constitutive electromagnetoelastic relations.Comparison between local and nonlocal analyses has been performed in this paper to justify necessity of this work.Monaco et al.[22]studied Linear stability of a nanoplate in a hygrothermomechanical environment with considering von-Karman geometric nonlinearity and NSGT.Some important works on the effect of magnetic loads in micro and nano scale and wave propagation may be observed in the references[23-33].
There are some works on the application of piezoelectric materials in energy application in various papers[34-47].Feng et al.[48]analyzed metal wave guides using manifold-coupled multiplexer.Chen et al.[49]studied the impact of small scale parameter associated with Eringen nonlocal elasticity theory on the reflection of planar wave in an electromagnetoelastic nanoplate immersed in liquid based on a three-dimensional analysis.First order state space system method and eigenvalues and eigenvectors method were used.Some researchers[50-56,78-81]studied effect of a fluid made of nanoparticles on the mechanical behaviors of lubrication shear strains,Ei,Hiare electromagnetic fields,Di,Biare electric displacement and magnetic induction,respectively.Based on MCST,mijand χijare defined as

in which

and

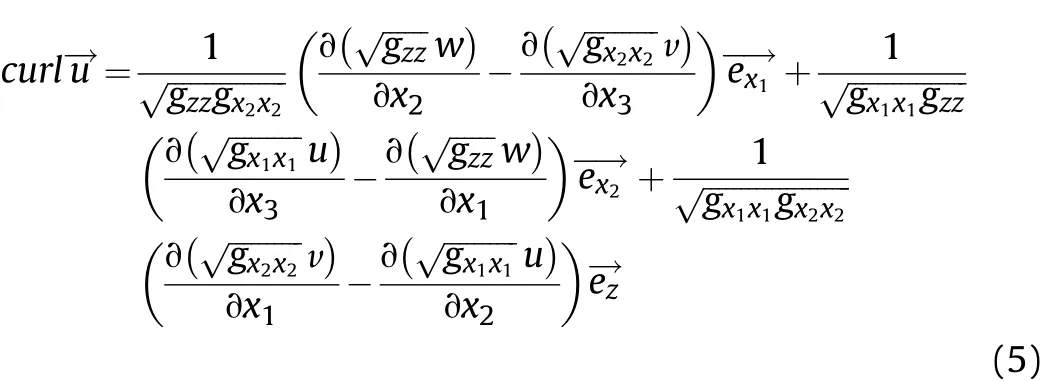
To derive governing and basic relations,we assume[62-64].
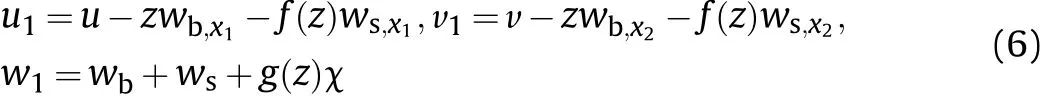
in whichu1,v1,w1are displacement field along the three perpendicular axis andwb,wsare bending and shear parts of transverse displacements(Fig.1).The variable deflection along the thickness direction is determined with χ as the thickness stretching function.It is expressed that the total deflection is summation of three sources.The first term in in-plane displacement is displacement of middle plane,the second term is linear rotation about middle plane and the third term is nonlinear rotation.The changes of displacements along the thickness direction is modelled through shape functionsf(z)=z-h/πsin(πz/h)andg(z)=1-f′(z).
Based on the displacement field defined in Eq.(6),thecurl u→is computed as

In addition,the components of curvature tensor are expressed as

Substitution of components ofinto Eq.(9)leads to v

The six strain components are computed using the assumed displacement field as follows:
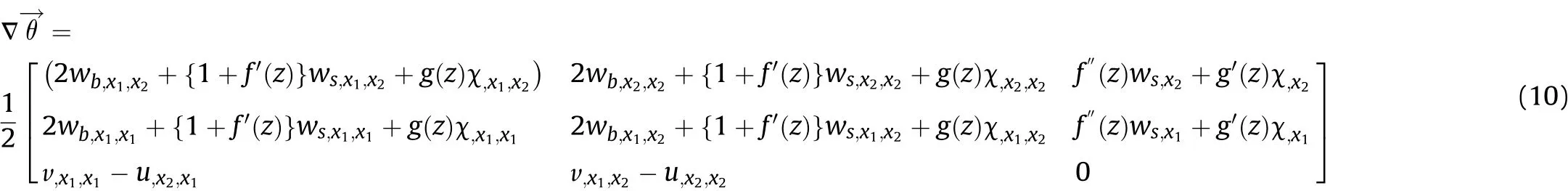
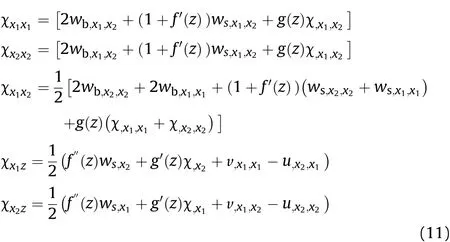
And finally using Eq.(4),we will have in which

The relations for piezoelectric/piezomagnetic media are extracted as

The multi-field constitutive relations are expressed as
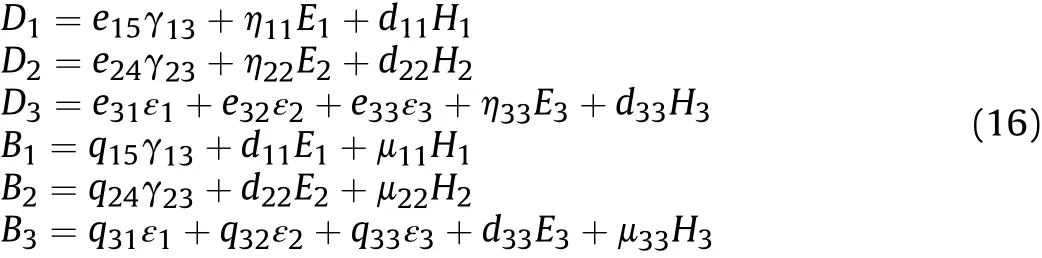
whereeij,ηij,dij,qij,μijare piezoelectric,dielectric,magnetoelectric,piezomagnetic and magnetic coefficients.
Constitutive relations for elastic middle layer is derived as follows:

Through definition of below components as presented in Appendix and,integration by part,the strain energy variation is computed as
Finally,the governing equations are derived as
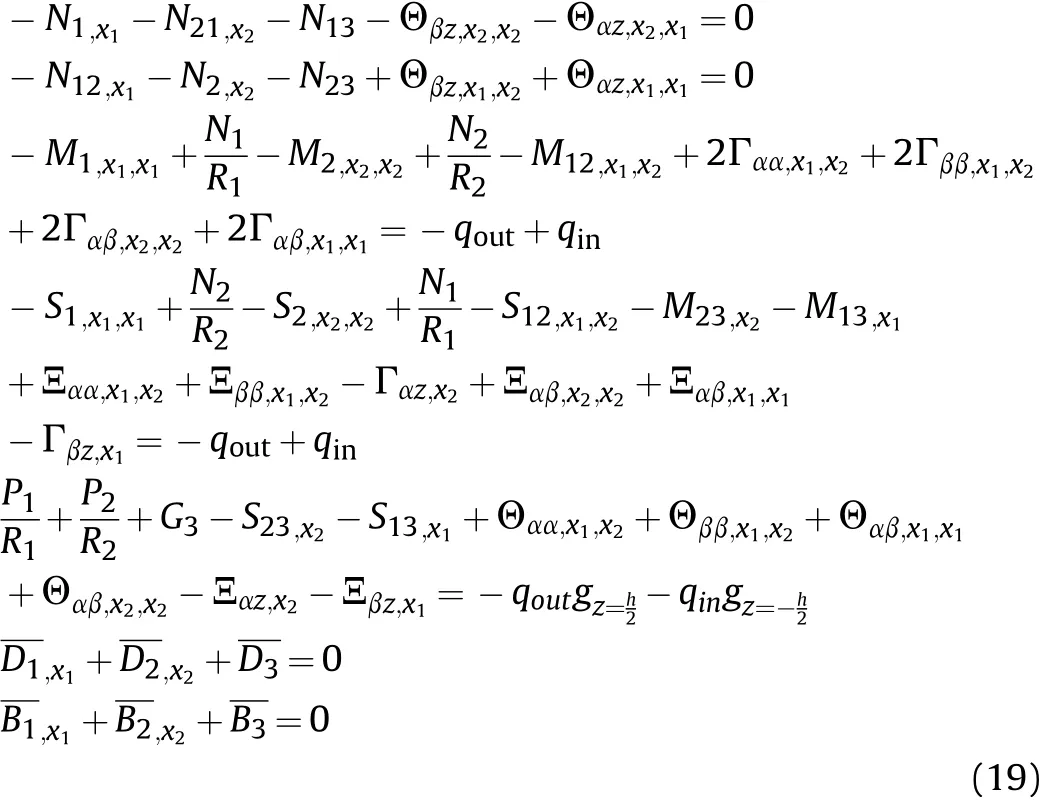
3.Solution
The electro-magneto-elastic bending results are derived based on the following solution using trigonometric functions as follows:

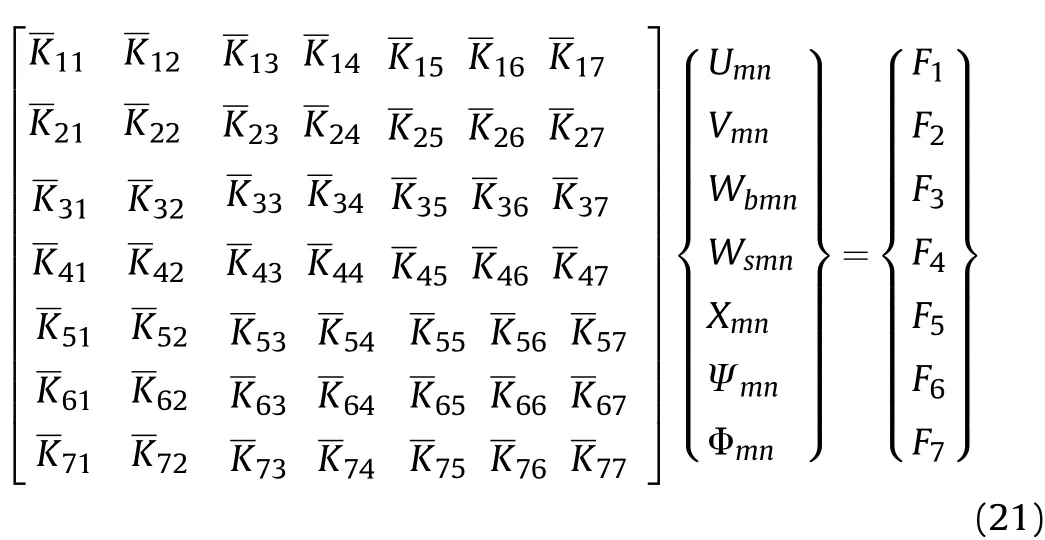
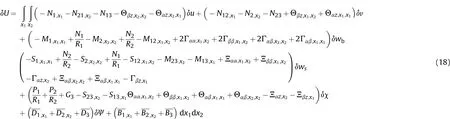
Because of very long terms of stiffness matrix,derivation of the first resultant componentN1and its substitution in the governing equation and finally in stiffness matrix is presented as
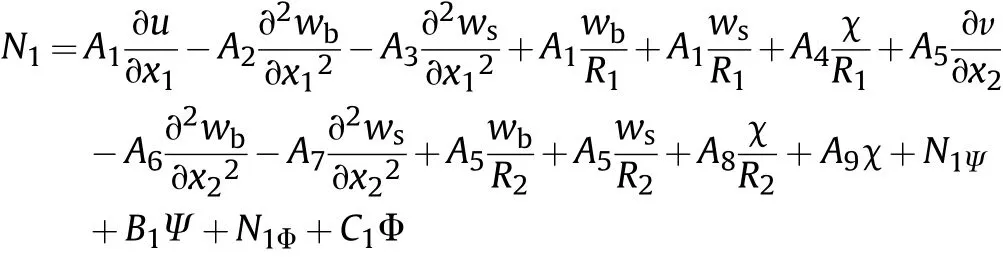
in which are integration constants depending on the material properties presented in Appendix.Applying the first derivative and substituting in the first governing equations constructs a part of stiffness matrix as follows:
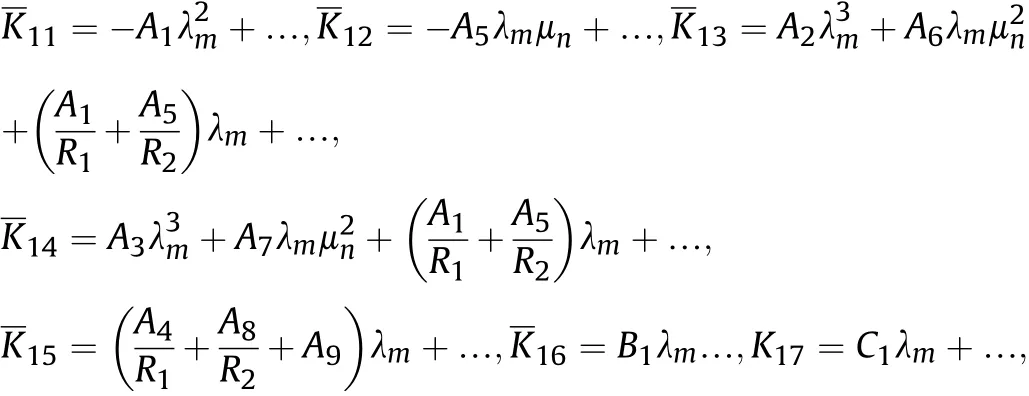
The same procedure may be continued for other resultant components and other governing equations to reach complete form of stiffness matrix.
4.Parametric analysis
This section presents the electro-magneto-elastic results of a doubly curved micro shell with accounting thickness stretching effect subjected to a combination electric,magnetic and mechanical loads in which the micro length scale parameter is changed to capture its effect on the responses.
Table 1 presents a comparison with results provided by Ref.[67]in macro scale through ignoring small scale parameter.An acceptable agreement is observed through this comparison.
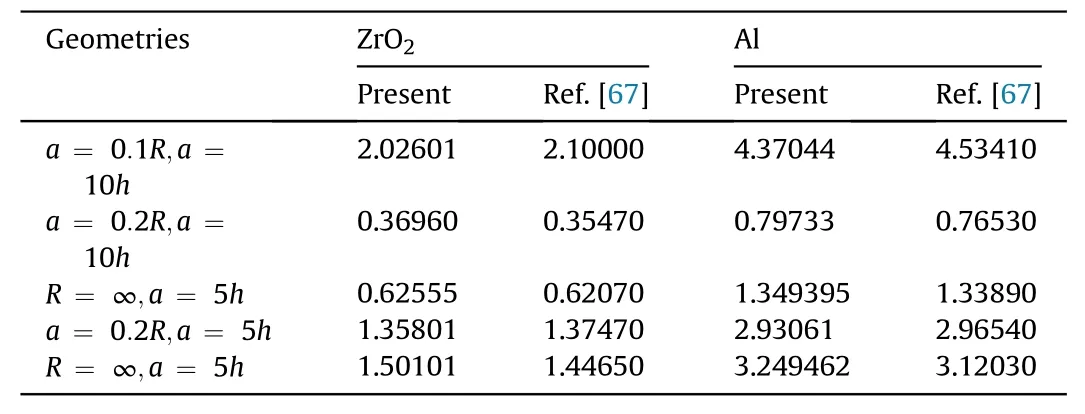
Table 1Comparison with results of Ref.[67].
Table 2Changes of with changes of Kw and Kg.

Table 2Changes of with changes of Kw and Kg.
?
The material properties of piezoelectric/piezomagnetic materials are assumed as
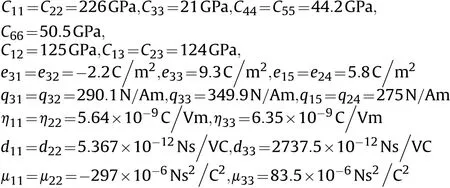
The basic geometries of the doubly curved shell is assumed as

Fig.2 depicts influence of micro length scale parameterNand initial electric potential Ψ0on the bending deflectionof micro shell.One can observe a decrease in bending deflectionwith an increase inNand Ψ0.A significant increase in structural stiffness of a micro structure may be observed with an increase in micro length scale parameterN.Furthermore,the initial electric potential has a decreasing effect on the bending deflection.Depicted in Fig.3 is changes of shear deflectionwith changes ofNand Ψ0.A concurrent decrease in bending deflection is observed with an enhance in micro scale parameter and initial electric potentials due to enhance in stiffness of the structure.The similar behaviour for bending deflection is observed for shear deflection.
Shown in Fig.4 is changes of in-plane displacementwith changes of micro scale parametersNand initial electric potentialA decrease in in-plane displacementis observed with an increase inNandA concurrent decrease in axial displacement of middle surface is observed with an enhance in micro scale parameter and initial electric potentials due to enhance in stiffness of the structure.
Effect of small scale parameters as well as initial electric potential is studied on the changes ofpotentials in Fig.5,Fig.6 respectively.The numerical results indicate that both maximum electric/magnetic potentials are decreased significantly with an increase in small scale parameter and initial electric potential.
Fig.2.Changes of dimensionless bending deflection wb with changes of N andΨ0.

Fig.3.Changes of dimensionless shear deflection with changes of N and

Fig.4.Changes of with changes of N and
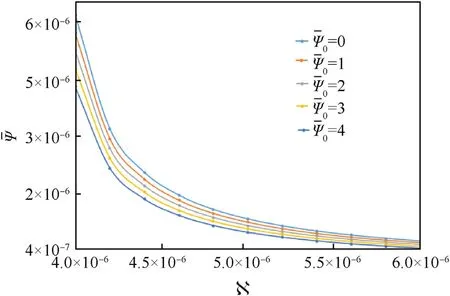
Fig.5.Changes of with changes of N and
Fig.6.Changes of Φ with changes of N and
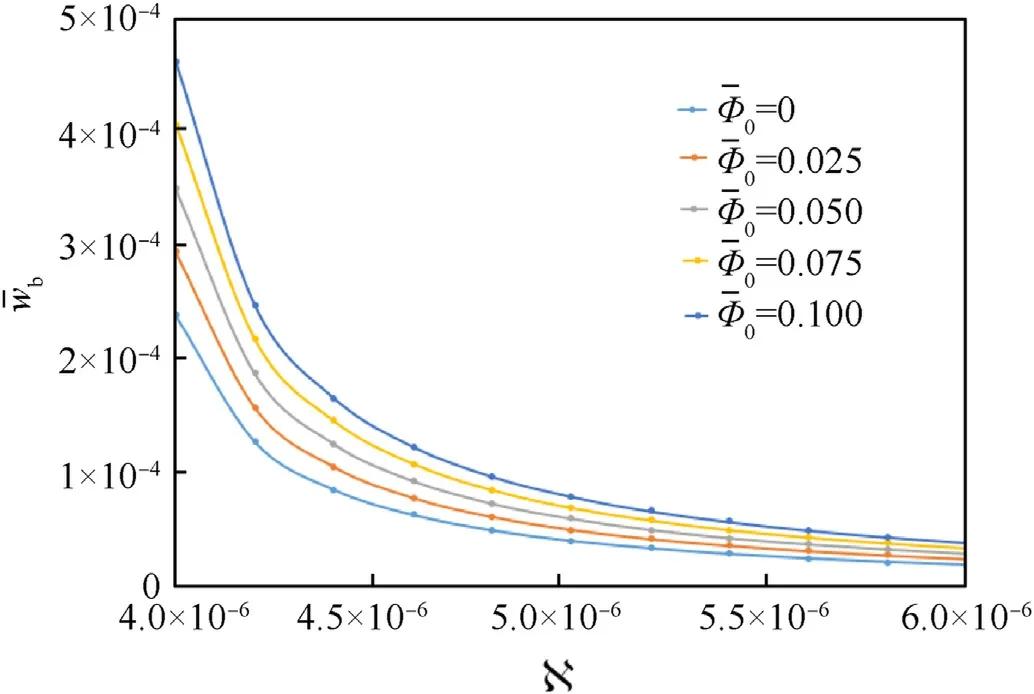
Fig.7.Changes of with changes of N and
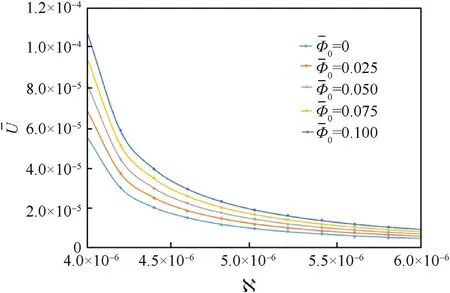
Fig.8.Changes of with changes of N and
A concurrent effect of initial magnetic potential Φ0and micro length scale parameter N on the changes of bending deflectionand in-plane displacementis studied in Fig.7,and Fig.8 respectively.An increase in bending deflectionand in-plane displacementUis observed with an increase in Φ0unlike increase in N that leads to significant decrease in all mentioned parameters.
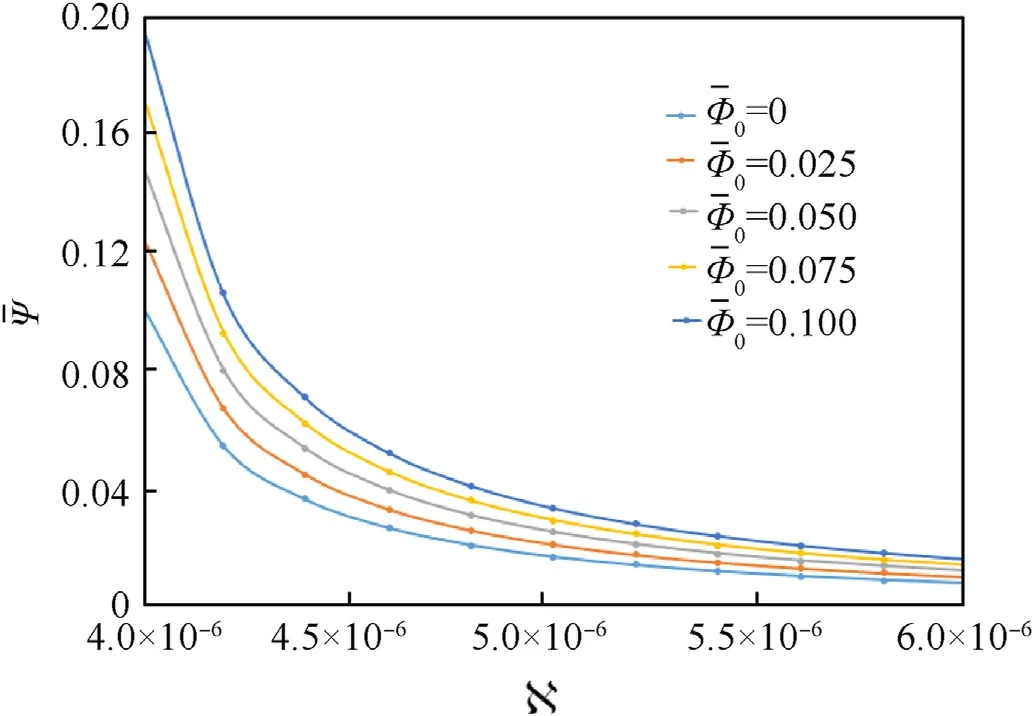
Fig.9.Changes of with changes of N and
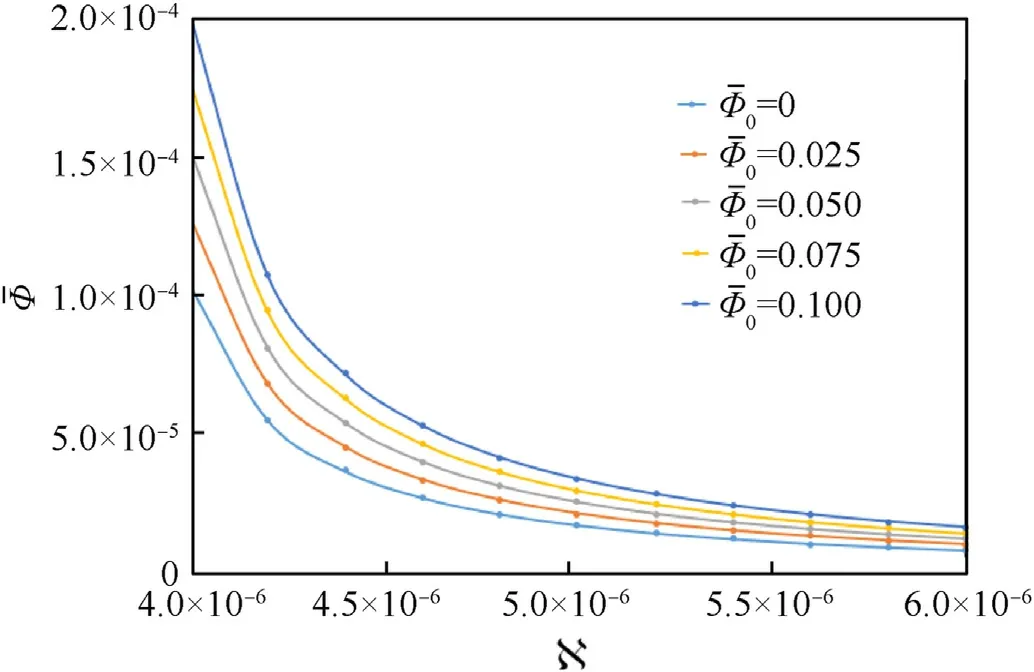
Fig.10.Changes of with changes of N and
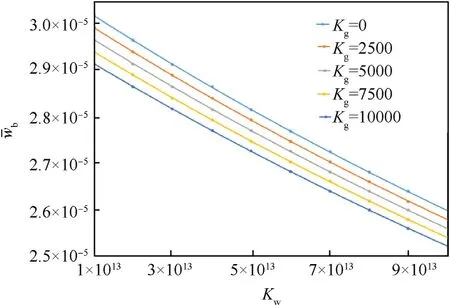
Fig.11.Changes of with changes of Kw and Kg.
Effect of small scale parametersNas well as Φ0is studied on the changes of maximum electric Ψ and magneticpotentials in Fig.9,Fig.10 respectively.The numerical results indicates that both maximum electric and magnetic potentials are increased significantly with an increase in
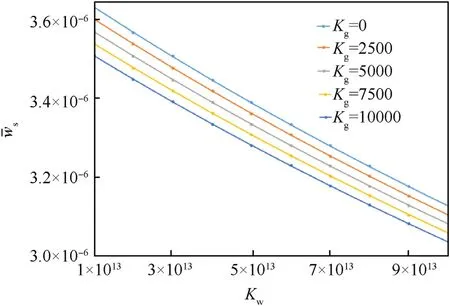
Fig.12.Changes of with changes of Kw and Kg.
Shown in Fig.11 and Fig.12 are changes of dimensionless bending and shear displacement with changes of two parameters of foundation,respectively.A decrease in all displacements is concluded with an increase in direct and shear parameters of foundation.Listed in Table 2 is changes ofwith changes ofKwandKg.
Listed in Table 3,Table 4 are changes of maximum electric and magnetic potentials with changes direct and shear parameters of foundation.A significant decrease in both maximum electric and magnetic potentials is observed with an increase in both input parameters.
5.Conclusions
Small scale dependent magnetoelectroelastic analysis of a doubly curved microshell was studied in this paper based on modified couple stress theory,higher order shear and normal deformation theory and principle of virtual work.The micro shell was composed of a micro core integrated with two piezoelectric/piezomagnetic layers as sensor and actuator.After derivation of the kinematic relation based on higher-order shear and normal deformation theory including thickness stretching effect,the modified couple stress theory was employed to derive higher-order stresses and strains.The electromagnetoelastic bending results are presented in terms of significant parameters such as initial electric/magnetic potentials,micro length scale parameter and parameters of foundation.The important results of this paper are classified as follows:
It was concluded that enhancing the micro length scale parameter leads to an enhancing in structural stiffness.
Investigating effect of multi-field loading on the electromagnetic bending results indicates that the deflections are decreased with an increase in electric potential as well as a decrease inmagnetic potential.
TCahbalneg3es of dimensionless maximum electric potential with changes of Kw and Kg.
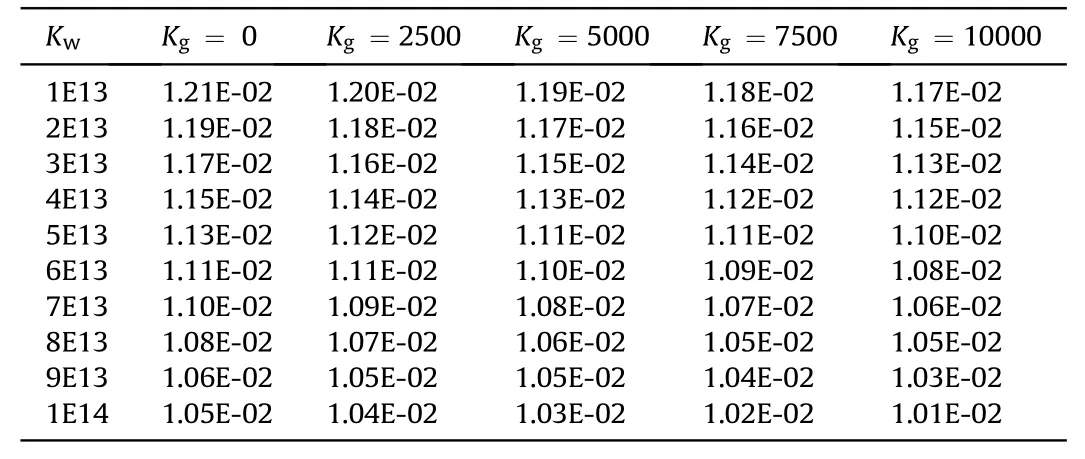
TCahbalneg3es of dimensionless maximum electric potential with changes of Kw and Kg.
?
TCahbalneg4es of dimensionless maximum magnetic potential with changes of Kw and Kg.
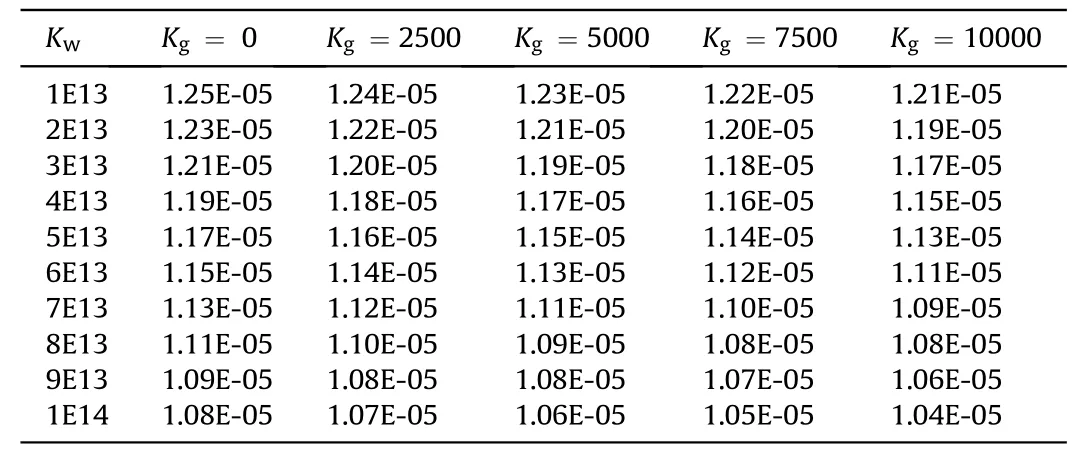
TCahbalneg4es of dimensionless maximum magnetic potential with changes of Kw and Kg.
?
Investigating effect of parameters of Pasternak’s foundation on the responses indicates that a decrease in all components is observed with an increase in the foundation’s parameters.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the Programs for Science and Technology Development of Henan province(No.202102210020)and Basic research plan of key scientific research projects of Henan universities(No.20B430011).
Appendix
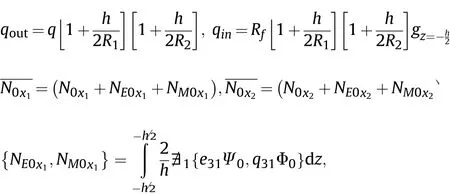


杂志排行
Defence Technology的其它文章
- Recent advances in the synthesis and energetic properties of potassium-based potential green primary explosives
- Investigation of normal,lateral,and oblique impact of microscale projectiles into unidirectional glass/epoxy composites
- A quasi-isentropic model of a cylinder driven by aluminized explosives based on characteristic line analysis
- Kevlar fabric reinforced polybenzoxazine composites filled with silane treated microcrystalline cellulose in the interlayers:The next generation of multi-layered armor panels
- Experimental study on the cavity evolution and liquid spurt of hydrodynamic ram
- Preparation of ammonium nitrate-based solid composite propellants supplemented with polyurethane/nitrocellulose blends binder and their thermal decomposition behavior
