一类非线性离散动力系统反周期解的存在性

孟鑫

（吉林师范大学 数学学院,吉林 四平 136000）

0 引言

反周期问题产生于一些物理过程的数学模型中,同时也经常出现在抽象微分方程和偏微分方程的研究中.由于离散动力系统在科学计算、控制理论和计算机科学等众多领域有着重要的应用,因此,离散动力系统的反周期解问题已成为众多学者近年来关注的一类重要问题[1-4].

在非线性微分方程以及非自治离散动力系统稳定性与定性理论的研究中,二分性理论已经成为一个重要的工具[5-6].常见的二分性有指数型二分性和普通二分性,具有指数型二分性系统的Green 函数是可求和的,具有普通二分性系统的Green 函数是一致有界的.关于指数型二分性在离散动力系统中的应用,已经有了一些基本的结论[7-9].Pinto 在文献[10]中提出可求和二分性的概念,文献[11-12]应用可求和二分性研究了差分方程系统收敛解的存在性问题.

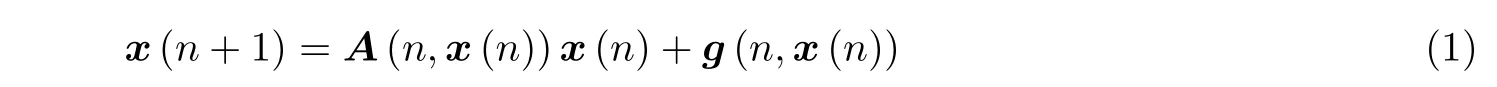
本文主要研究非线性离散动力系统的反周期解存在性.应用可求和二分性条件以及Banach 不动点定理,给出系统(1)反周期解存在唯一的充分条件,并通过例子说明主要结果在实际问题中的应用.

1 预备知识

在本文中,Z表示整数集,R表示实数集,当a,b∈Z且a＜b时,记[a,b]={a,a+1,···,b}.|·|表示Eucli d范数,设l∞(Z)={x:Z→Rd:x在Z上有界},若设,则l∞(Z)是Banach空间.

系统

其中,A:Z×Rd→Rd×d,u:Z→Rd,x:Z→Rd.设Φu(n)是系统(2)的基本解矩阵,若存在投影P,以及常数K1,K2＞0,α1,α2＞0,使得

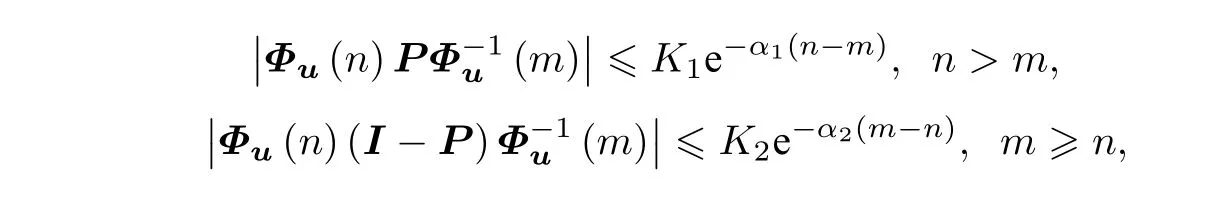
其中,I是d阶单位矩阵,e是自然常数,则称系统(2)具有指数型二分性.

若存在投影P和常数µ＞0,使得系统(2)的Green 函数

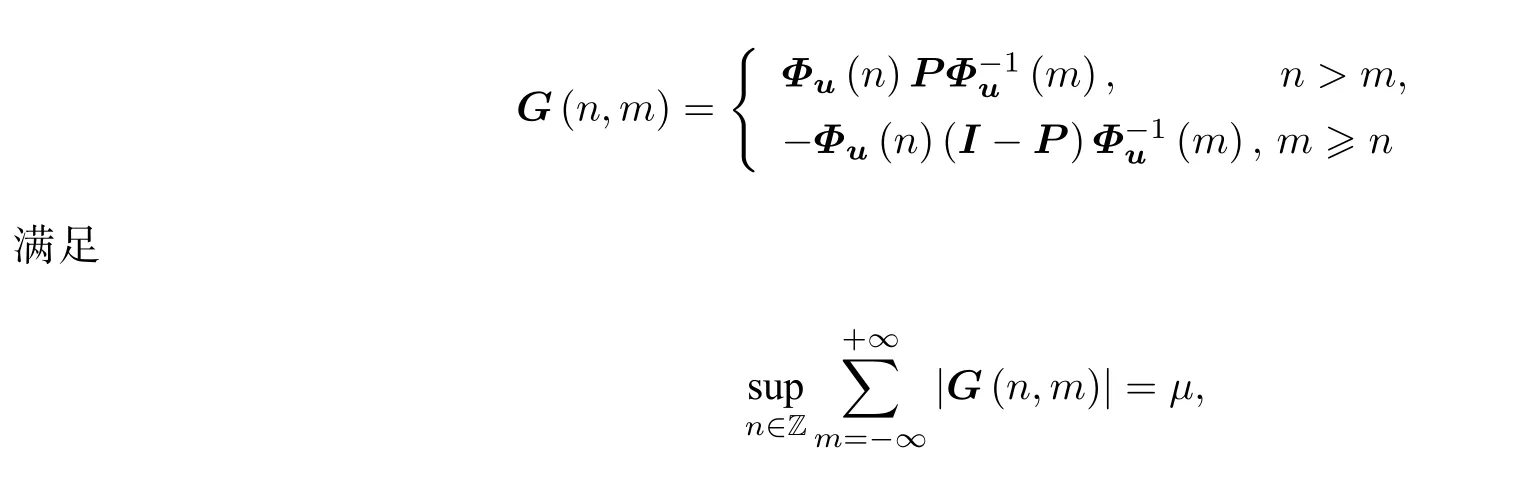
则称系统(2)具有可求和二分性.

显然,若系统(2)具有指数型二分性,则系统(2)具有可求和二分性.

设N是正整数,考虑N-反周期系统

是系统(3)的有界N-反周期解.

证明显然xu(n)是系统(3)的解,并且

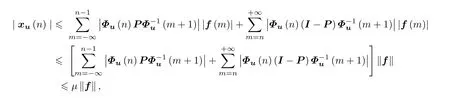
故xu(n)是有界的.

若Φu(n)是系统(2)的基本解矩阵,且,则Φu(n+N)也是系统(2)的基本解矩阵,且对任意m,n∈Z,有

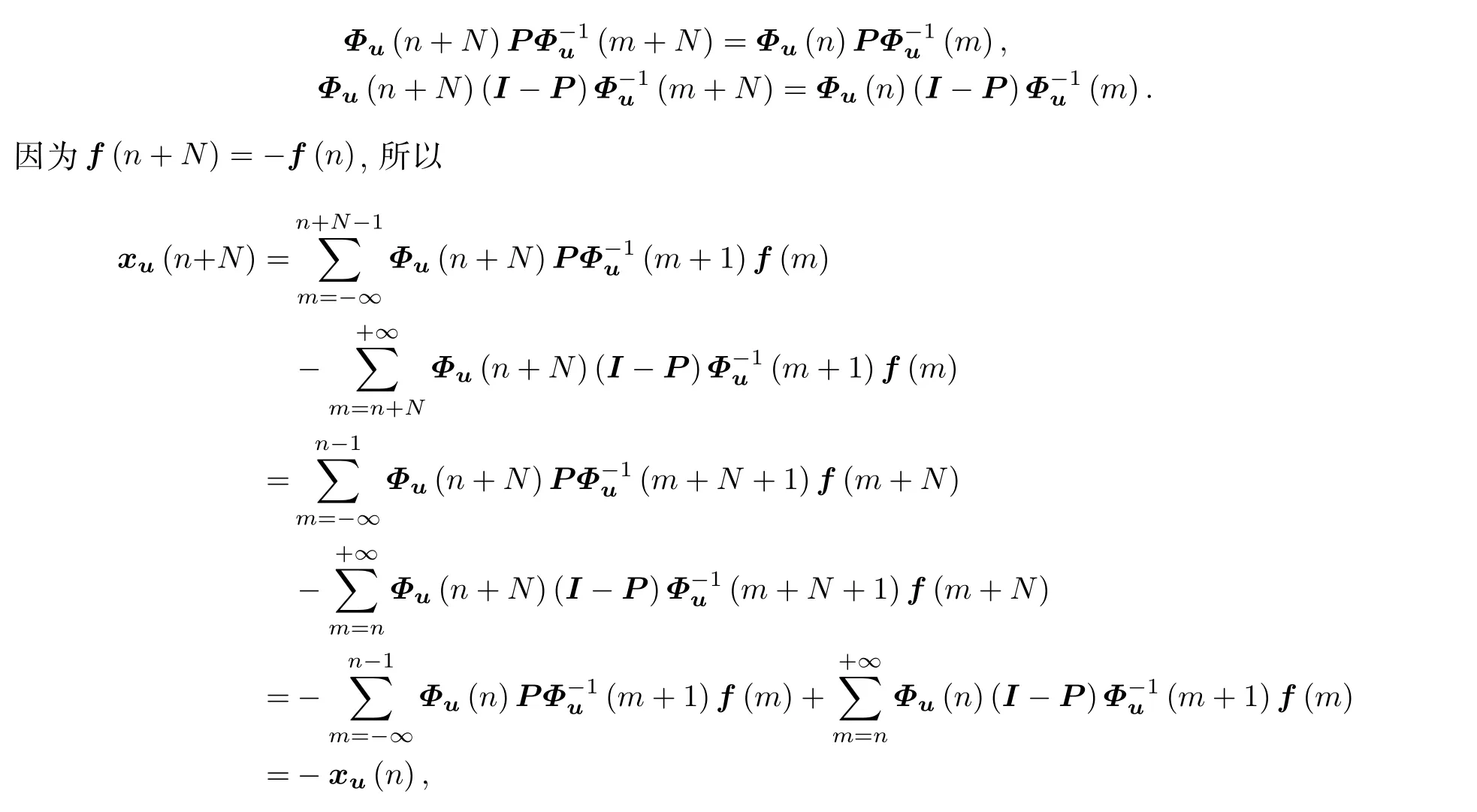
故xu(n)是N-反周期的.

因此,xu(n)是系统(3)的有界N-反周期解.

2 主要结果

考虑系统(1),其中x:Z→Rd,A:Z×Rd→Rd×d,g:Z×Rd→Rd,给出如下几个条件.

(H1) 对任意n∈Z和x∈Rd,

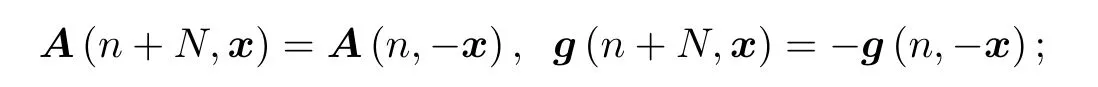
(H2) 系统(2)关于投影P和常数µ＞0 具有可求和二分性;

(H3) 存在常数L＞0,使得

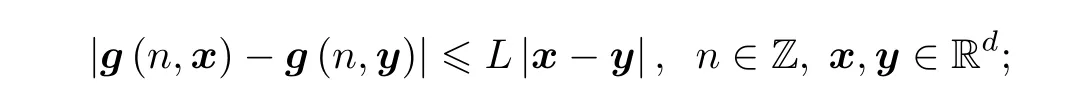
(H4) 存在有界函数L:Z→[0,+∞),使得

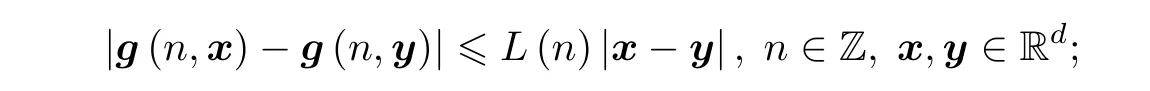
(H5) 存在函数L:[0,+∞)→[0,+∞),对任意λ＞0,n∈Z,当x,y∈Rd,且|x|≤λ,|y|≤λ时,

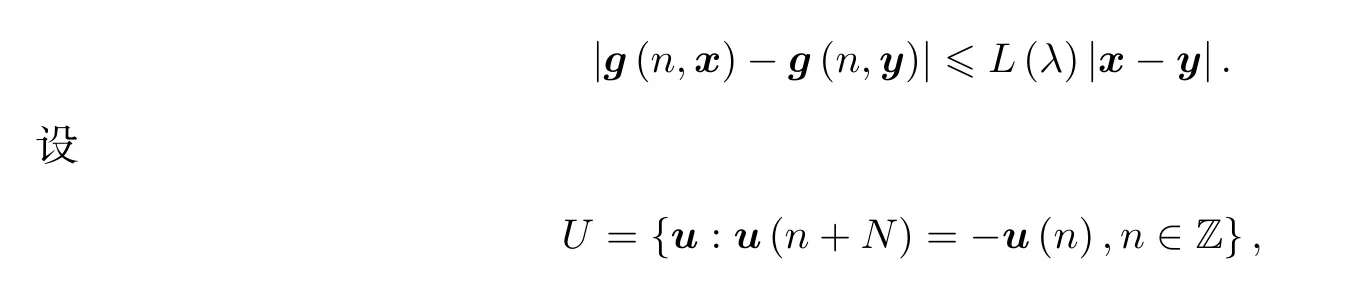
其中,u:Z→Rd,并且定义U上的范数为为Banach 空间.

定理 1设条件(H1)—(H2)及 (H4)成立,若,则系统(1)有唯一的N-反周期解.

证明考虑N-反周期系统

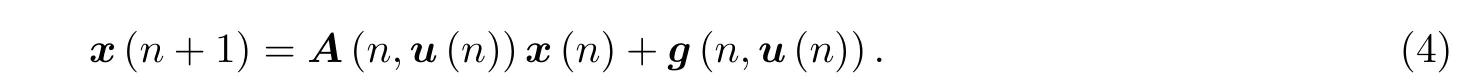
根据条件(H1)和命题1,系统(4)的解为

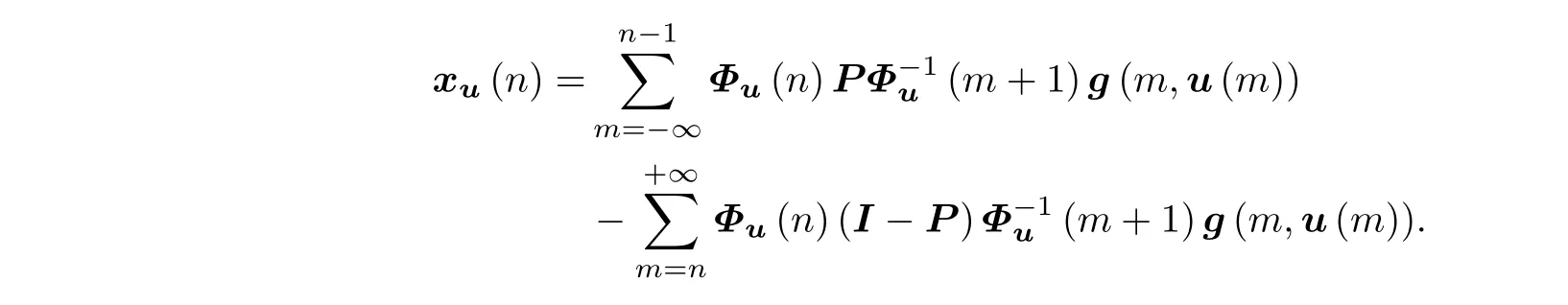
类似于命题1,对任意n∈Z,当

定义映射T:U→U为

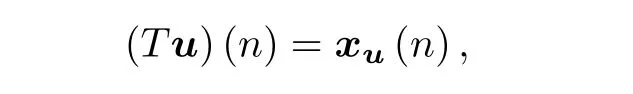
则T的不动点即为系统(1)的N-反周期解.对任意u1,u2∈U,根据条件(H2)和(H4),

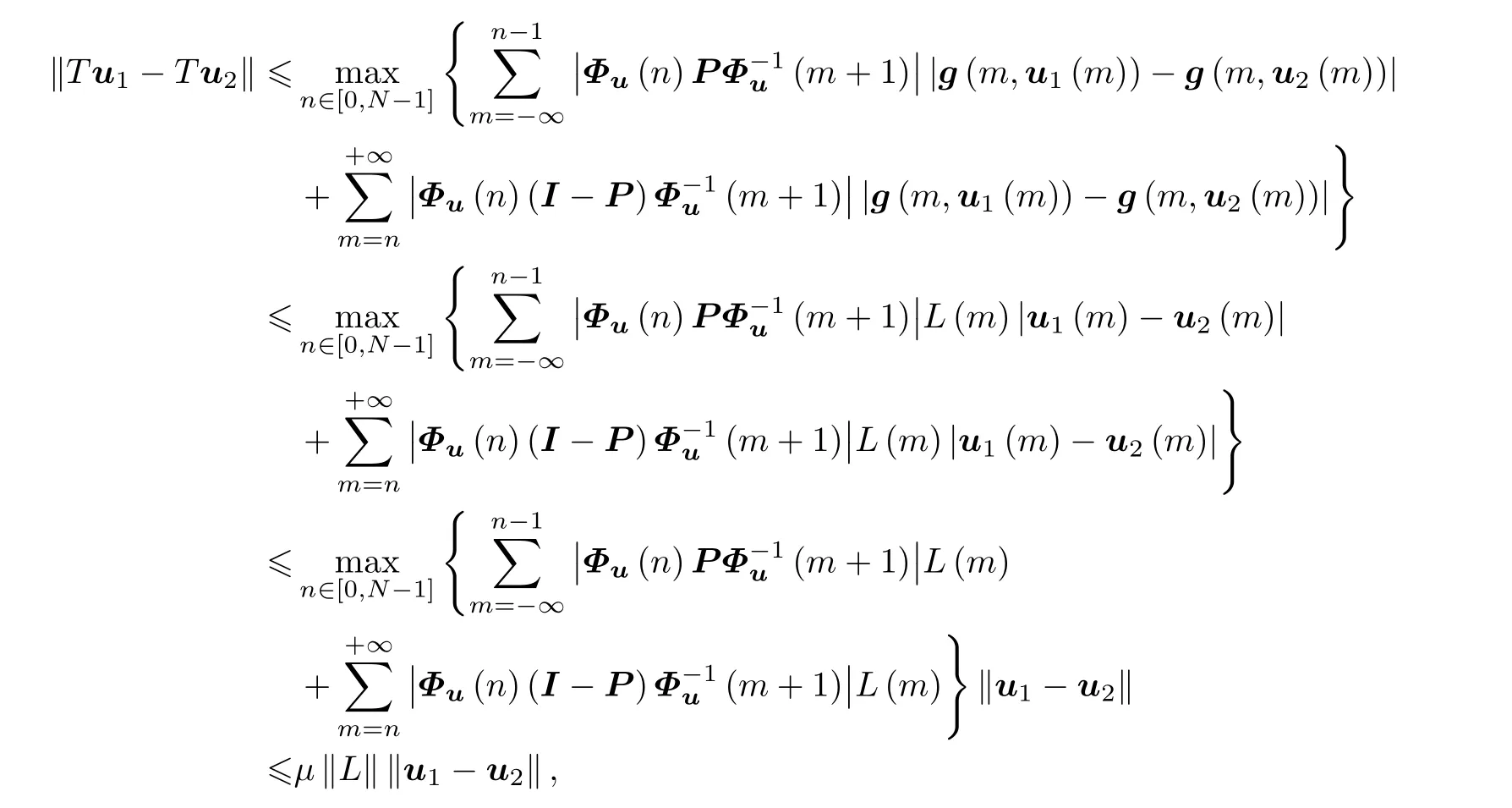
故T是U上的压缩映射,根据Banach 不动点定理,映射T有唯一不动点,从而系统(1)有唯一的N-反周期解.

推论 1设条件(H1)—(H3)成立,若,则系统(1)有唯一的N-反周期解.

设λ＞0,

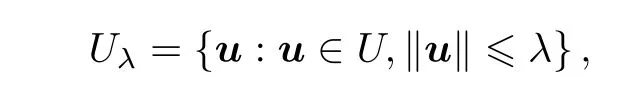
其中,u:Z→Rd,并且Uλ上的范数为为Banach 空间.

3 结论

应用Banach 不动点定理,在系统x(n+1)=A(n,u(n))x(n) 具有可求和二分性的条件下,给出非线性离散动力系统

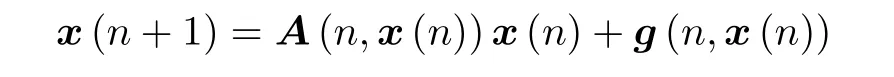
存在反周期解的两个充分条件,并应用主要结果证明了系统

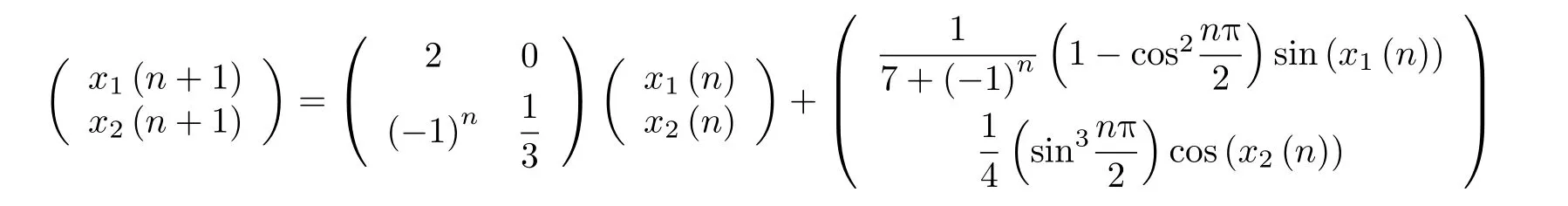
存在 2-反周期解.