非规则圆柱面壁画的高分辨率全景图像生成法
2022-11-25何伟童卫青
何伟,童卫青,2
(1.华东师范大学 计算机科学与技术学院,上海 200062;2.上海商务数码图像技术有限公司,上海 200041)
0 引言
洞窟壁画的数字化保存不但可以有效地保护文物,还可以利用这些数字化数据进行数字文物展览等二次开发利用.国家文物局发布的《古建筑壁画数字化测绘技术规程》规定,壁画文物的一级影像采样分辨率不能低于300 DPI (Dots Per Inch).这意味着对幅面比较大的壁画,目前任何高分辨率的相机都无法只通过拍摄一张图像就可以采集到壁画的全部数据.
因此,一般先对壁画进行网格化分割;然后对每个小网格区域用高分辨率相机进行图像采集;最后把每个网格区域图像 (一般有上百幅图像) 拼接成一幅全景图像.全景图像拼接是指把多视角、低分辨率、局部重叠的系列图像,通过某种图像处理方法拼接成一张具有高分辨率、宽视角的图像.这是一个比较热门的研究领域,其已在文物数字化保存、遥感图像、土地资源监控[1]、气象云图、车载全景影像[2-3]、医学影像[4]、红外目标追踪[5]等许多领域得到了实际应用.图像拼接大概可以分成两大类:一类是在二维图像空间进行拼接;另一类是在三维图像空间进行拼接.
在二维图像空间进行图像拼接研究得比较充分.早期比较经典的图像拼接技术是1970 年由Anuta等[6]提出的基于Fourier-Mellin 变换的图像配准算法.随后,Kuglin等[7]和De Castro等[8]从相位相关性角度提出了图像匹配法,该方法在很大程度上克服了平移和旋转变换对图像拼接的影响.1993 年,Djamdji等[9]提出了基于图像小波变换特征点的图像配准算法.1999 年,SIFT (Scale-Invariant Feature Transform) 由Lowe[10-11]提出.SIFT 不仅可以提取稳定的图像特征,还可以用来描述这些特征,对图像分辨率、仿射变换、光照和噪声等变化具有非常强的鲁棒性;此后SIFT 特征被广泛应用于图像配准,成为图像拼接中具有里程碑意义的技术.2004 年,基于角点检测的Harris 算法在图像拼接中得到应用[12].2006 年,Bay等[13]提出了基于积分图像和盒子滤波器的SURF (Speeded-up Robust Features) 算法,该算法降低了特征提取的运算量,提高了图像配准的效率.2011 年,Rubble等[14]提出了ORB (Oriented FAST and Rotated BRIEF)算法,该算法的性能接近于SIFT,但处理速度要明显高于SIFT.Brown等[15]从空间平面间的映射关系角度提出了非常新颖的AutoStitch 拼接法,该方法的核心是采用了全局单应性对齐处理;由于该方法只使用1 个单应性矩阵,所以对有景深的图像拼接会产生重影.随后Gao等[16]提出了DHW (Dual-Homography Warping) 算法,该算法将图像划分成远近2 个层面,用2 个单应性矩阵分别对前景图像和背景图像进行变换,减少了图像内部的景深差异,解决了大部分场景的无缝拼接问题.为了提高处理视差、增加局部变形上限和获取更好的图像对齐效果,Lin等[17]提出了采用多个仿射变换的SVA (Smoothly Varying Affine)算法.2013 年,Zaragoza等[18]提出了APAP (As-Projective-As-Possible)算法,该算法将图像划分为长宽一致的小网格,让每个小网格单独用1 个单应性矩阵对齐,增加了局部变化的自由度,从而提高了拼接效果.2016 年,Chen等[19]提出了GSP (Global Similarity Prior) 算法,该算法在APAP 基础上增加了全局转换矩阵选取方面的处理,对直线对齐进行约束以获取最佳角度,提高了图像拼接性能.随着人工神经网络技术的高速发展,该技术在图像拼接中也开始得到了初步应用[20-23].
在三维图像空间对多视图进行全景图拼接,其处理流程: 先把二维的多视图转换到三维成为三维图像;然后再从三维空间正投影到二维空间,从而获得一张二维全景图.这方面的研究起步较晚,研究成果不多.2016 年,刘礼铭[24]提出了一个基于三维重建的壁画数字化框架,首次在平面壁画的数字化中应用了三维重建技术.由于手工拓片方式对碑刻文物会带来一定程度的损坏,国家禁止对珍贵碑刻文物进行手工拓片.因此,张园林[25]运用三维模型对碑刻的数字拓片生成进行了研究,开发了碑刻数字拓片生成系统.为了降低三维重建算法得到的三维模型与ground-truth 数据之间的误差,闫冰[26]对上述问题进行了优化处理研究,提高了重建模型的质量.大部分基于图像的三维重建方法是基于物体表面的纹理特征进行的,当物体表面纹理较弱时重建后的三维模型将缺乏精细性,对此李敏[27]提出了基于非朗伯体的光度立体的三维重建算法.针对多视图三维重建的特征匹配环节所存在的匹配时间复杂度较高和鲁棒性较差的问题,李淑芬[28]提出了基于局部几何约束的自适应特征匹配方法,从而使文物数字化更加快速和真实.
对于大幅面平面壁画的全景图,可以使用上述的基于二维图像空间和三维图像空间的方法进行生成.但对于大幅面非规则圆柱面壁画的全景图生成,根据研究调查目前似乎还停留在使用二维空间的图像拼接方法.对于近似平面的壁画,在拍摄时只要让相机与壁画保持垂直和恒定距离,那么采用上述基于特征配准的拼接算法就可以获得比较好的全景图.但是,对于大幅面非规则圆柱面壁画就不能采用这样的方法,这是一个比较有挑战性的课题.本文提出了能有效生成大幅面非规则圆柱面壁画的数字全景图像的方法 (Cylindrical Panoramas Generation,以下简称CPG 算法).CPG 算法处理流程: ①按恒定距离采集两两重叠的多视角图像;② 检查出多视角图像的SIFT 特征的匹配点;③从匹配点获得稀疏点云;④ 从稀疏点云获得稠密点云;⑤ 根据稠密点云进行三维建模;⑥ 通过单应矩阵把多视图的纹理信息映射到三维模型的三角片面上,生成壁画的三维图像;⑦ 将非规则圆柱面的三维图像映射到其外接理想圆柱面上;⑧ 将理想圆柱面按最佳对称轴进行展开,并正投影到最佳平面,从而获得二维全景图像.
1 三维圆柱面壁画图像重建
本文CPG 算法: 第一阶段通过采用图像集构建其对应的三维模型;第二阶段通过三维模型生成二维全景图.图1是CPG 算法的处理流程图.在CPG 算法的三维重建处理中,对图像的重叠率有一定的要求,对于平面图像只需要达到50%的重叠率;而对于圆柱面图像,其重叠率需要达到50%~70%.
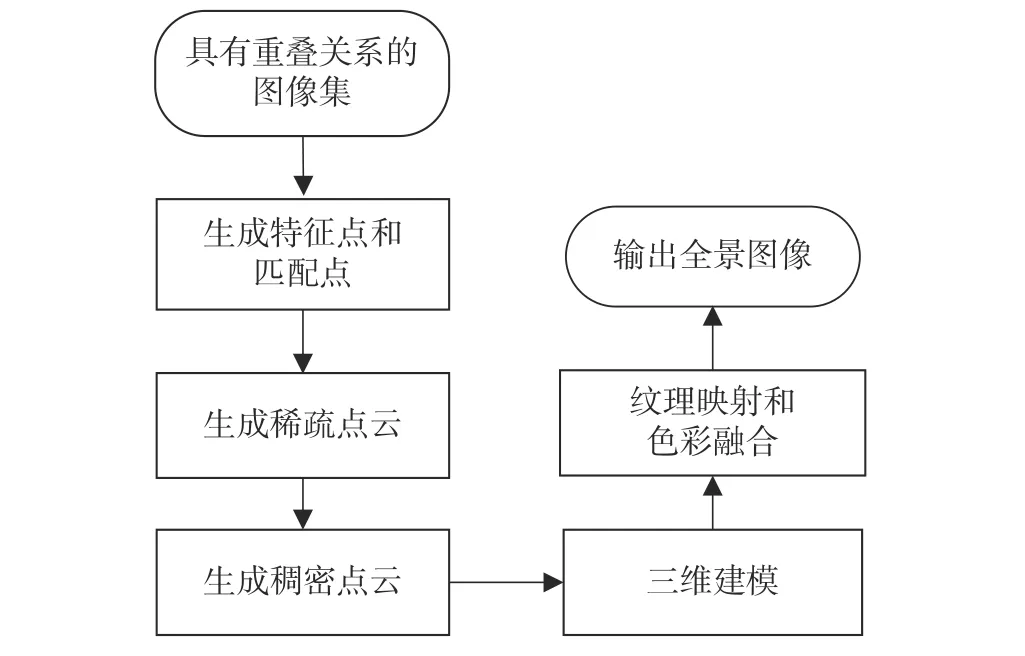
图1 CPG 算法流程图Fig.1 Flow chart of CPG algorithm
CPG 算法的三维重建处理流程如下.
1) 图像匹配点
运用SIFT 算法对每张图像提取特征点,并通过基于局部区域的暴力匹配方法获取每幅图像的匹配点.
2) 稀疏点云
依据匹配点,采用SFM (Structure From Motion)[29]算法生成稀疏点云.SFM 算法能够利用2 个或2 个以上场景恢复出相机的内在参数和外部参数.SFM 算法寻找一对最合适的图像(这2 幅图像有部分区域是重叠的)作为基准视图,以该基准视图的三维点为基础,一边估算相机姿态一边不断加入新视图的三维点来迭代拓展,并利用光束平差法BA (Bundle Adjustment)[30]来最小化每次加入新视图所带来的误差.
3) 稠密点云
仅仅得到稀疏点云还不足以重建三维模型.对此,本文CPG 算法采用了Shen[31]提出的基于深度图融合的稠密点云生成方法: 首先,对每一个图像的像素通过空间传播和随机分配这两个操作步骤,计算其深度图;然后再将其融合来表示目标场景,即生成目标场景的稠密点云.
4) 三维建模
根据文献[32]提供的利用可视信息来确定弱支持表面的方法,将稠密点云进行基于Delaunay三角剖分,以构成表面的三角网格;然后利用稳定的三角结构构建出能还原表面细节的模型.
5) 纹理映射和色彩融合
Waechter 等[33]在 2014 年提出了基于马尔可夫随机场的纹理映射方法,该方法首先对三角网格面片的纹理图像进行挑选,再对全局和局部的颜色进行色彩融合.本文的CPG 算法采用了该纹理映射方法来进行纹理映射处理.
通过以上步骤,就完成了CPG 算法的第一阶段的三维重建任务,达到了利用现有算法进行二次开发的目的.下一章将对CPG 算法的第二阶段—全景图像生成算法做详细介绍,这也是本文CPG 算法的重点部分.
2 三维圆柱面壁画图像转换成平面全景图像
由于实际洞窟里的石柱形状往往不是理想圆柱面,并且这些石柱面也不光滑,常常有微小的凹凸不平.因此,从数学角度来说,这些非规则圆柱面是无法展开成平面的.
鉴于此,本文提出了CPG 的第二阶段算法: 利用第一阶段所生成的三维模型把非规则圆柱面图像展开成平面全景图像.第二阶段算法的具体流程如图2 所示,其主要步骤: ①首先把实际非规则圆柱面拟合成1 个理想的圆柱面;② 然后把非规则圆柱面上的图像信息映射到理想圆柱面上;③在世界坐标系中,把理想圆柱面展开成空间平面;④ 最后把空间平面按指定图像分辨率要求投影成全景图像.下面按上述4 个步骤介绍具体的处理方法.
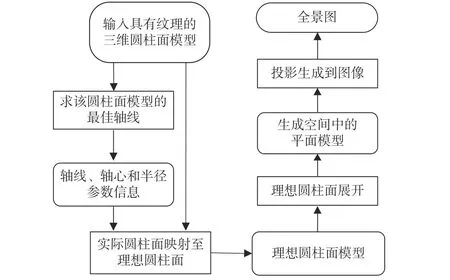
图2 全景图生成流程图Fig.2 Flow chart of panorama generation
2.1 求理想圆柱面参数
由第1 章可以得到实际的非规则圆柱面壁画的三维图像Icylinder,该三维图像提供了空间任意点的六维信息(x,y,z,R,G,B),即该点的空间坐标 (x,y,z)和彩色信息 (R,G,B) .本节将介绍如何找到1 个理想圆柱面Iics,使其非常接近于非规则圆柱面Icylinder.
不失一般性,这个理想圆柱面Iics可以由图3来表示.图3中,坐标系Oxyz是世界坐标系;Rics为Iics的半径;P0(x0,y0,z0)是Iics的中心轴线上的参考点;(l,m,n)是Iics的中心轴线的方向数,记为P(x,y,z)是Iics面上的任意点.根据圆柱面的几何性质,只要确定了Iics的半径Rics、中心轴线和其参考点P0,那么Iics就可被完全确定.由于Iics的中心轴线可以通过其方向数 (l,m,n) 来确定,所以只要求出(x0,y0,z0,l,m,n,r) 这7 个参数值就可以获得Iics.理想圆柱面可以看作到1 个定向中心轴线距离等于某常数的点的集合,由此可得Iics的参数方程
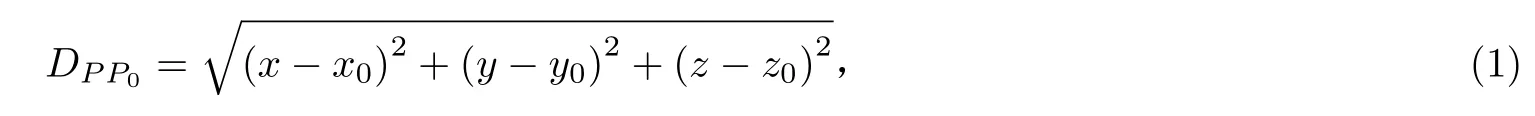
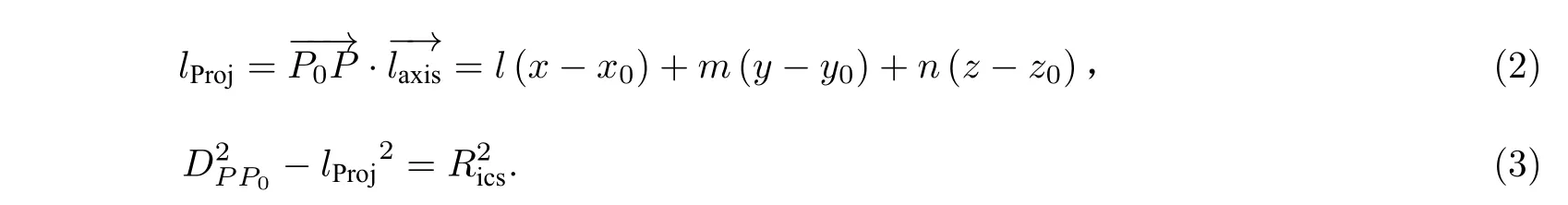
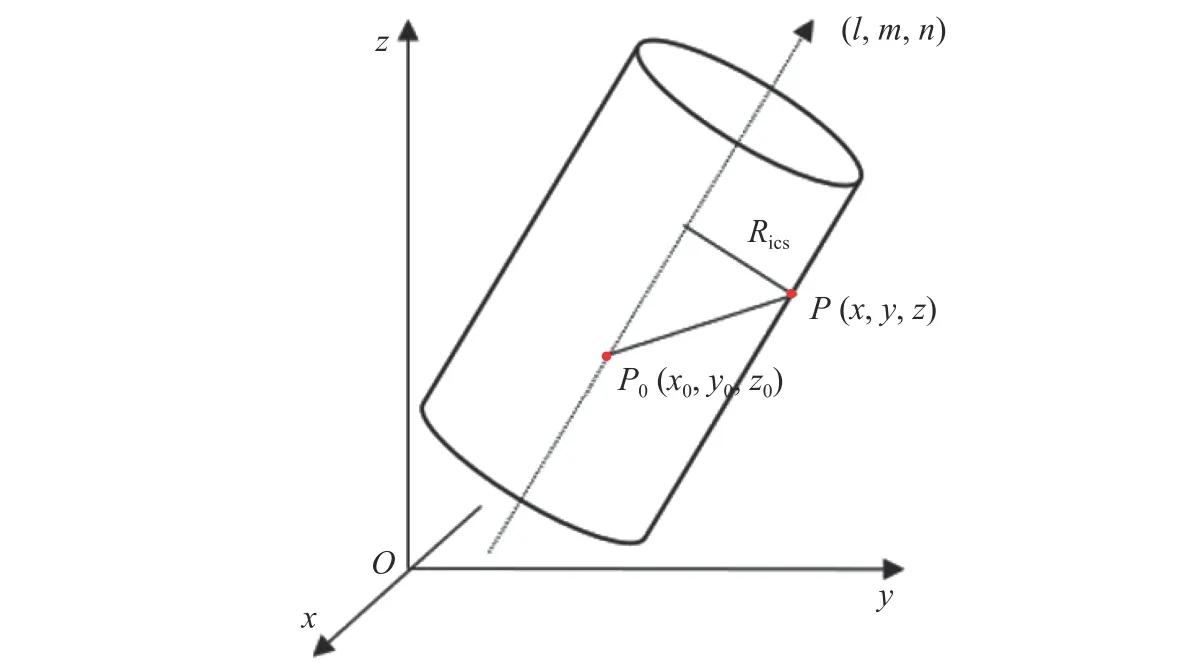
图3 参数方程的几何表达Fig.3 Geometric expression of parametric equation
对式(3)采用最大似然一致性算法MLESAC (Maximum Likelihood Estimation Sample And Consensus)[34]进行处理,就可以得到理想圆柱面Iics的方程的解,从而找到三维图像Icylinder的1 个最佳的拟合理想圆柱面Iics.
2.2 实际圆柱面向理想圆柱面映射
2.1 节解决了由实际圆柱面拟合成理想圆柱面的问题.本节介绍如何把实际圆柱面映射到理想圆柱面.
第一步,对实际圆柱面和理想圆柱面进行坐标变换,使Iics的中心轴线laxis和参考点P0(x0,y0,z0)分别与世界坐标系的z轴和原点O重合.由图4 可以获得2 个参数的计算公式,具体为

式(4)—(5)中:θ是中心轴线laxis的方向向量与z轴的夹角;是z轴的单位向量;是三维模型的旋转轴.
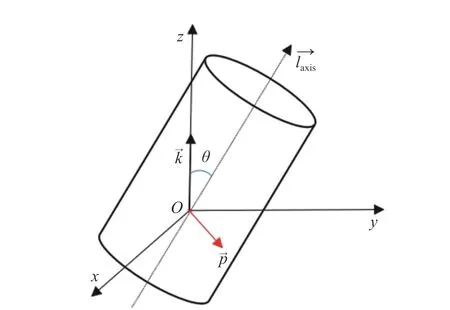
图4 圆柱面旋转Fig.4 Rotation of cylindrical surface
根据罗德里格斯旋转公式所计算出的旋转矩阵Rrotation,相应公式为
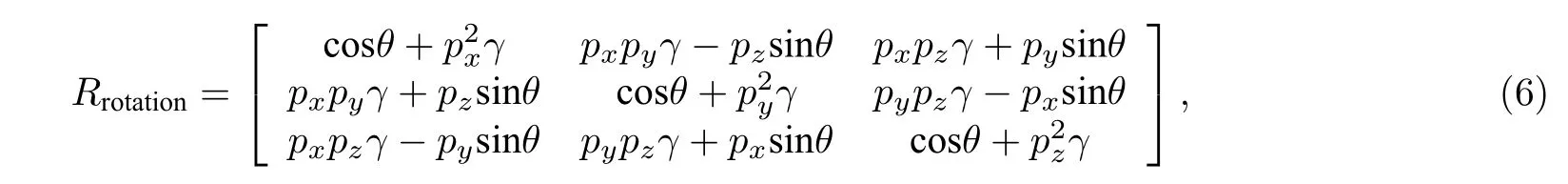
以及平移矩阵Rtranslation(平移矩阵为轴心到坐标原点的偏移量),可以得到实际圆柱面坐标变换前后的关系式
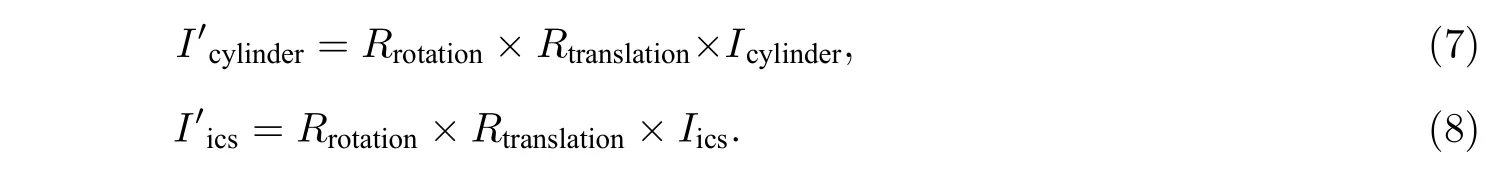
式(6)中:px,py,pz分别为向量的x,y,z坐标;
完成实际圆柱面坐标的变换后,第二步便是找到实际圆柱面上与理想圆柱面上点与点之间的映射关系.如图5 所示,设P(x,y,z) 为坐标变换后实际圆柱面I′cylinder上的点,Ocircle(0,0,z) 为在坐标轴z上与点P具有相同z坐标的点,p′(x′,y′,z) 为直线POcircle与I′ics的交点,即点P在理想圆柱面上的映射点,则直线POcircle方程和圆方程分别为

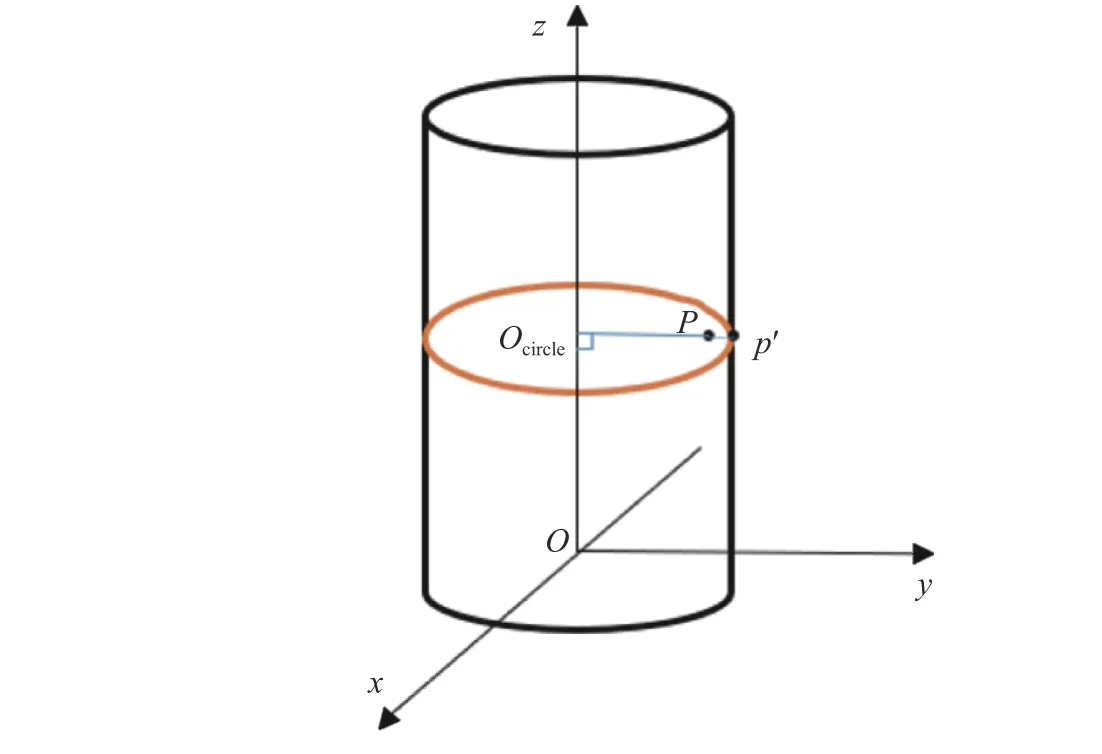
图5 实际三维点映射至理想圆柱面Fig.5 Map the actual 3D points to ideal cylindrical surface
解式(9)—(10)就可以获得P的映射点p′(x′,y′,z) .实际圆柱面空间点映射至理想圆柱面的具体设计见算法1.


2.3 在世界坐标系中理想圆柱面的展开
2.2 节完成了把实际圆柱面向理想圆柱面I′ics的映射处理.本节介绍如何将理想圆柱面I′ics在世界坐标系中展开.
图6是理想圆柱面映射至世界坐标系中的平面展开原理图.图6 中,为展开后的展开平面,Lz是平面与I′ics的切线,沿着切线Lz把I′ics展开成平面PICS(圆柱体表面展开所得到的平面),即展开在平面上,平面PICS与坐标平面zy平行.设I′ics上的点为p(xp,yp,zp),其在展开平面PICS上对应点为,则由图6 可知,这2 个点的对应关系符合公式
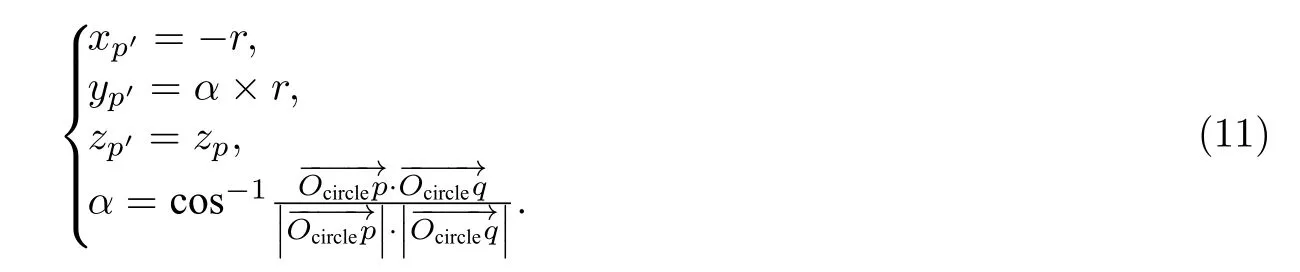
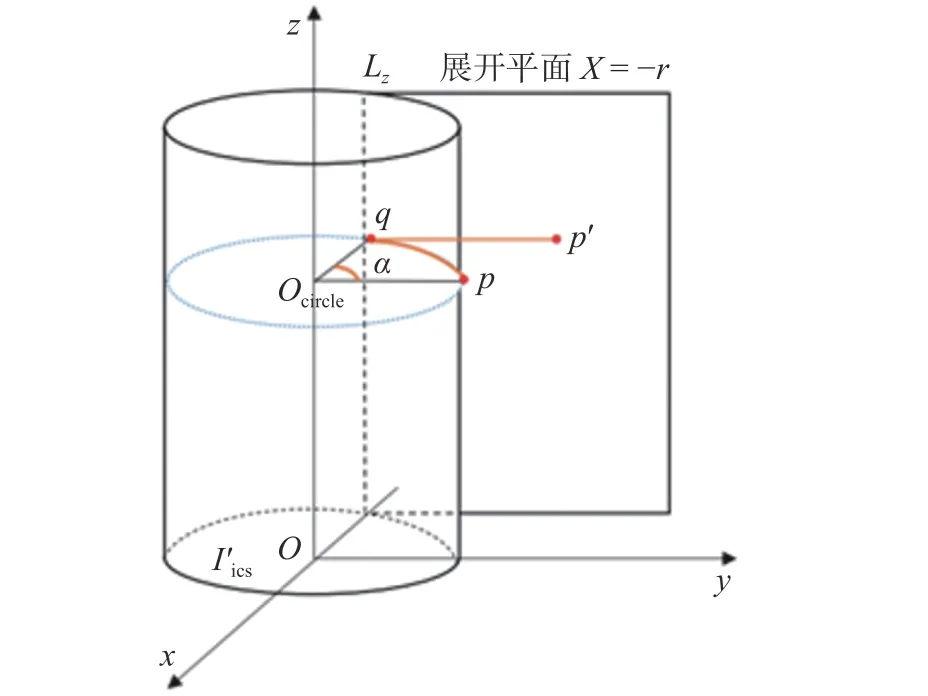
图6 理想圆柱面映射至世界坐标系中的平面Fig.6 Map the ideal cylindrical surface to a plane in world coordinates
这里需要指出的是,若三角网格被展开线Lz所穿过,那么其上的点必须在展开平面PICS的左右两端都要出现,以保证图像在左右两边都保持完整,这是由于柱面的封闭性所决定的.
理想圆柱面展开的具体实现流程见算法2.

2.4 全景图像生成
到2.4 节为止,把实际圆柱面壁画图像在世界坐标系中展开成了1 幅三维空间的平面图像.本节介绍如何把世界坐标系中的三维平面图像Isp映射到二维空间的全景图像Ipano.
把三维空间的平面图像Isp映射到二维图像空间的全景图像Ipano需要解决两个问题: 第一个问题,Isp在世界坐标系中进行三维建模时,其坐标是没有具体单位的 (或者称抽象单位),而它投影到二维图像空间后的Ipano图像,采用的单位是像素,为此要处理从抽象度量单位到像素度量单位的转化;第二个问题,Isp是在世界坐标系下的空间平面图像,它是建立在三维模型之上的 (这里采用的是三角面片三维表明建模),而全景图像Ipano是在二维图像平面上,它采用的是整数网格点平面.因此,需要处理这两种不同坐标系下的投影变换,即从连续三维空间向离散图像空间的转化.
上述的第一个问题其实等价于如何确定全景图像Ipano的分辨率M×N,即不需要知道Isp图像中的x,y,z坐标的实际单位,只要能把Isp图像投影到具有指定分辨率M×N的图像平面上就行.如果知道实际圆柱面的最大半径Rmax(inch)、最大高度Hmax(inch)和最低采样分辨率(Sample Resolution,SR)RSRmin(DPI),就能算出全景图像Ipano的分辨率 (M ×N) 像素(pixel),于是就解决了第一个问题.
全景图像Ipano的分辨率M×N由

确定后,就按图7 所示的方法: 先将三维空间平面Isp图像上的点利用主成分分析PCA (Principal Component Analysis) 算法,将空间三维点降为二维的点,而这些二维点依旧保持着三维点所有的三角网格的关系;然后以单个三角网格为单位把纹理投影至以32 位浮点数据为类型的图像I′上,此时该图像在数学意义上仍是连续的;最后对连续图像I′进行采样,生成分辨率大小为 (M ×N) 像素、8 位整型数据结构的图像.图7 坐标系仅用于表示三维空间;坐标系的方向不影响三维空间投影,任意方向皆可做到这一点.
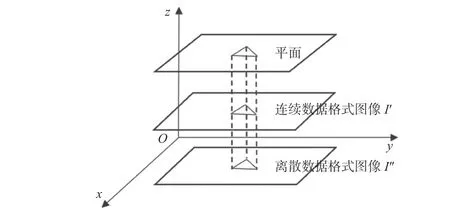
图7 正投影示意图Fig.7 Schematic diagram of orthographic projection
3 实验评估
为了评估本文所提出的非规则圆柱面壁画全景图像生成算法 (CPG 算法) 的有效性,本文首先制作了4 个典型图像集,这4 个图像集各自对应的实物图见图8;然后在这4 个图像集上分别运行CPG 算法和其他3 个典型算法,以此来比较和评估这4 种算法的性能.其他3 个典型算法如下.
(1) OpenCV 里的Stitching 算法 (以下简称OpenCV 算法),该方法可以把1 组相邻部分具有重叠的图像拼接成1 幅全景图像.
(2) OpenPano 算法是文献[15]里提出的生成全景图像的方法,该方法: ①先从输入图像中提取特征点和匹配点;② 选取匹配点最多的前几个图像作为候选图像,利用Ransac 寻找每个图像对的单应矩阵,使用概率模型验证图像是否匹配;③寻找匹配图像的连接部分,对每个连接用光束平差法对相机参数进行优化处理,最后使用多波段混合渲染出全景图.
(3) PhotoShop 算法,该方法是PhotoShop 软件提供的,能将1 组相邻部分具有重叠的图像拼接成1 幅全景图像的算法.

图8 4 个图像集各自对应的实物图Fig.8 Corresponding physical images of four image sets
3.1 实验用图像集的制作
1) 图像集A
图像集A是对虚拟圆柱面图像用虚拟相机进行采集而得到的106 张分辨率为(1 542 × 926)像素的图像,该图像集中相邻图像都有50%以上的重叠.其制作过程: 先用3ds Max 软件建立1 个三维圆柱面模型;然后把数字中国地图①数字中国地图来源于网站map.ps123.net,地图审图号为GS(2011)1 537 号.映射到所建的三维圆柱面上 (图8 (a));最后用具有飞思IQ180 参数的虚拟相机 (焦距为80 mm) 进行采集.图9 为图像集A 的部分样例,即后续实验部分用于放大比较的区域.
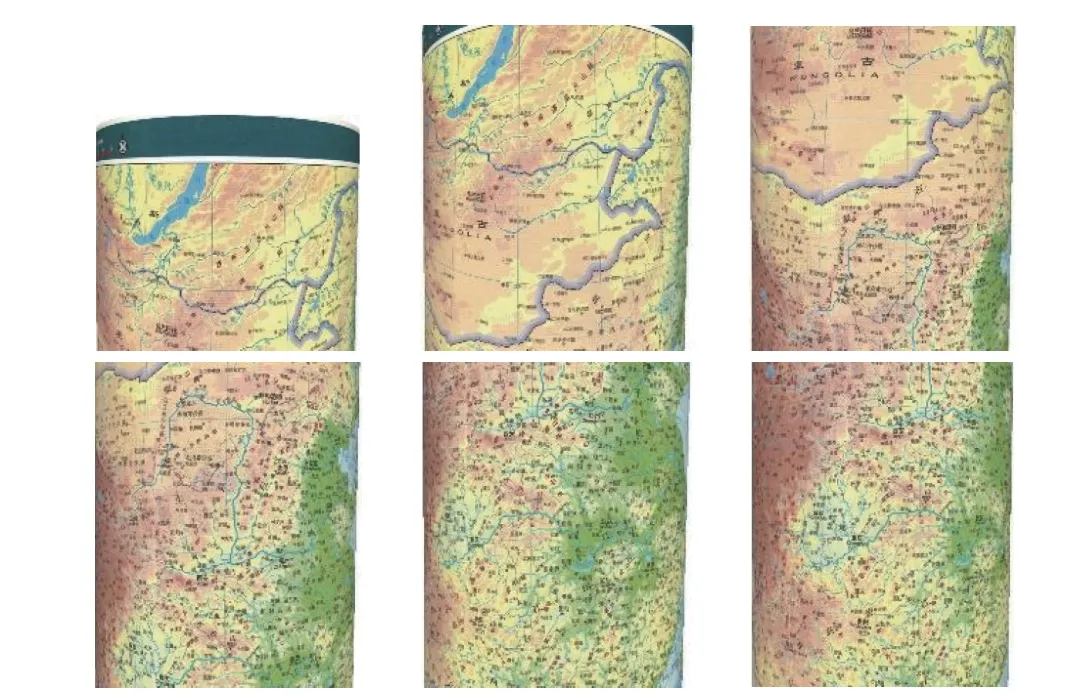
图9 图像集A 的部分样例Fig.9 Examples of image set A
2) 图像集B
图像集B是从新疆克孜尔第17 窟–甬道的近似圆柱面顶部 (图8(b)) 采集的143 张分辨率为(4 032 ×3 024)像素的图像.该甬道空间较为狭小,顶部壁画近一半以上有缺损.图10 为图像集B 的部分样例,该图像集中相邻图像都有50%以上的重叠,展示的区域即后续实验部分用于放大比较的区域.

图10 图像集B 的部分样例Fig.10 Examples of image set B
3) 图像集C
图像集C是从新疆克孜尔新1 窟–后室的近似圆柱面顶部(图8 (c))采集的142 张分辨率为(6 000 ×4 000)像素的图像.图8 (c)是从其顶部不同区域拍摄的3 张顶部壁画图像,该顶部约有1/4 部分有缺损.图11 为图像集C 的部分样例,该图像集中相邻图像都有50%以上的重叠,所展示的区域即后续实验部分用于放大比较的区域.
4) 图像集D
图像集D是从新疆克孜尔17 窟–前室的近似圆柱面顶部(图8 (d))采集的124 张分辨率为(6 000 ×4 000)像素的图像.图8 (d)是从其顶部不同区域拍摄的3 张顶部壁画图像,该顶部约有1/2 部分有缺损.图12 为图像集D 的部分样例,该图像集中相邻图像都有50%以上的重叠.

图11 图像集C 的部分样例Fig.11 Examples of image set C

图12 图像集D 的部分样例Fig.12 Examples of image set D
3.2 基于图像集A 的评估实验
本文实验首先在图像集A 上运行CPG 算法,目的是考察该算法对理想圆柱面上的纹理进行三维拼接和全景图展开的效果.图13 (a)是图像集A 的原始三维圆柱面地图,图13 (b)是由CPG 算法生成的三维圆柱面地图,从图13 (b)中可以看到,CPG 算法可以完整地从106 幅重叠的二维图像中生成其三维图像.
然后再对其全景展开图进行比较分析.图14 (a)是图像集A 对应的三维圆柱面地图的原始二维地图,即图8(a)所示的映射到三维模型的表面纹理;图14 (b)是通过CPG 算法对106 幅采集图处理后生成的二维全景图.对比图14 的这2 幅图,可以得到结论: 全景展开图中看不出106 幅采集图像的拼接痕迹和色彩变化,也看不出字符、线条出现模糊和扭曲变形的情形.
根据此实验,可以发现OpenCV 算法、OpenPano 算法和PhotoShop 算法都无法将数据集A 拼接成1 幅全景图像.为了与CPG 算法比较,本文从图像集A 中抽取东经110°附近的8 张图像作为图像集A 的子集,用于测试OpenCV 算法、OpenPano 算法和PhotoShop 算法.测试后发现,OpenCV 算法连这个子集都无法正常运行,OpenPano 算法和PhotoShop 算法的运行结果分别如图15 的左图和图16的左图所示,其各自右图是左图上红色区域的放大图.

图13 三维圆柱面地图Fig.13 3D cylindrical map
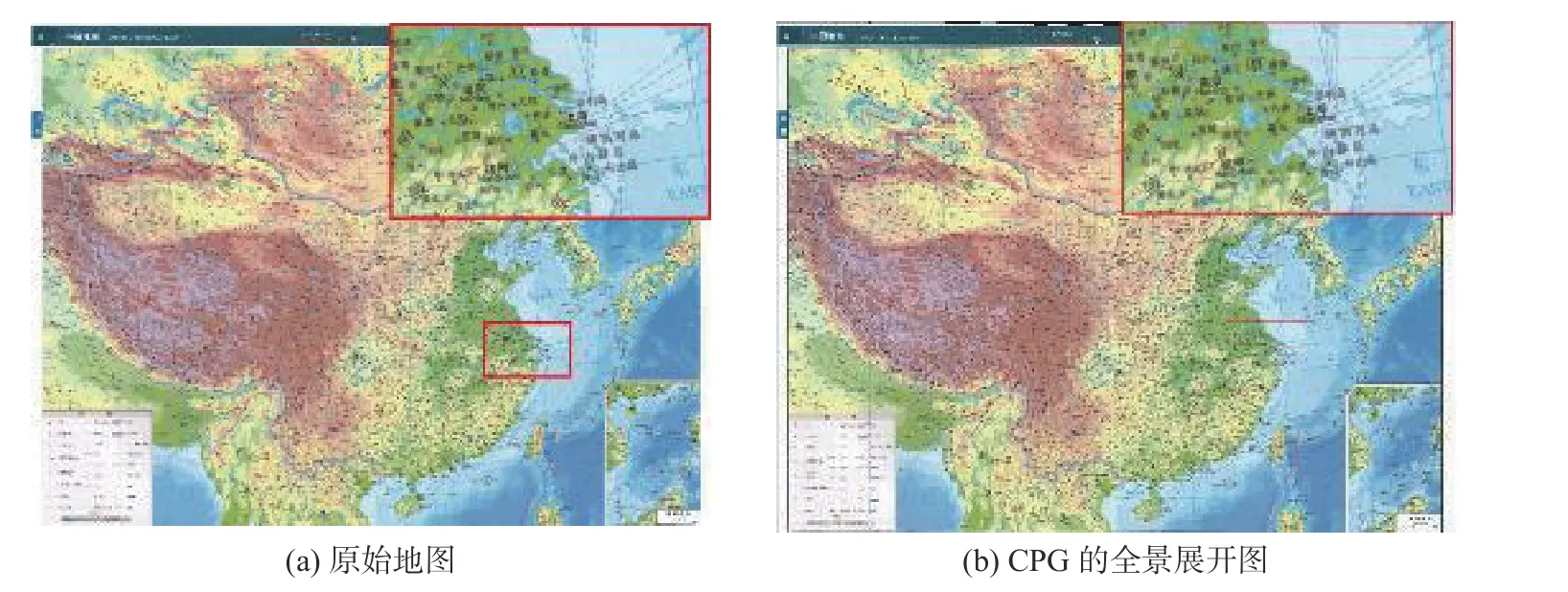
图14 原始图和CPG 算法的全景展开图比较Fig.14 Comparison between the original image and panoramic expanded image of CPG algorithm
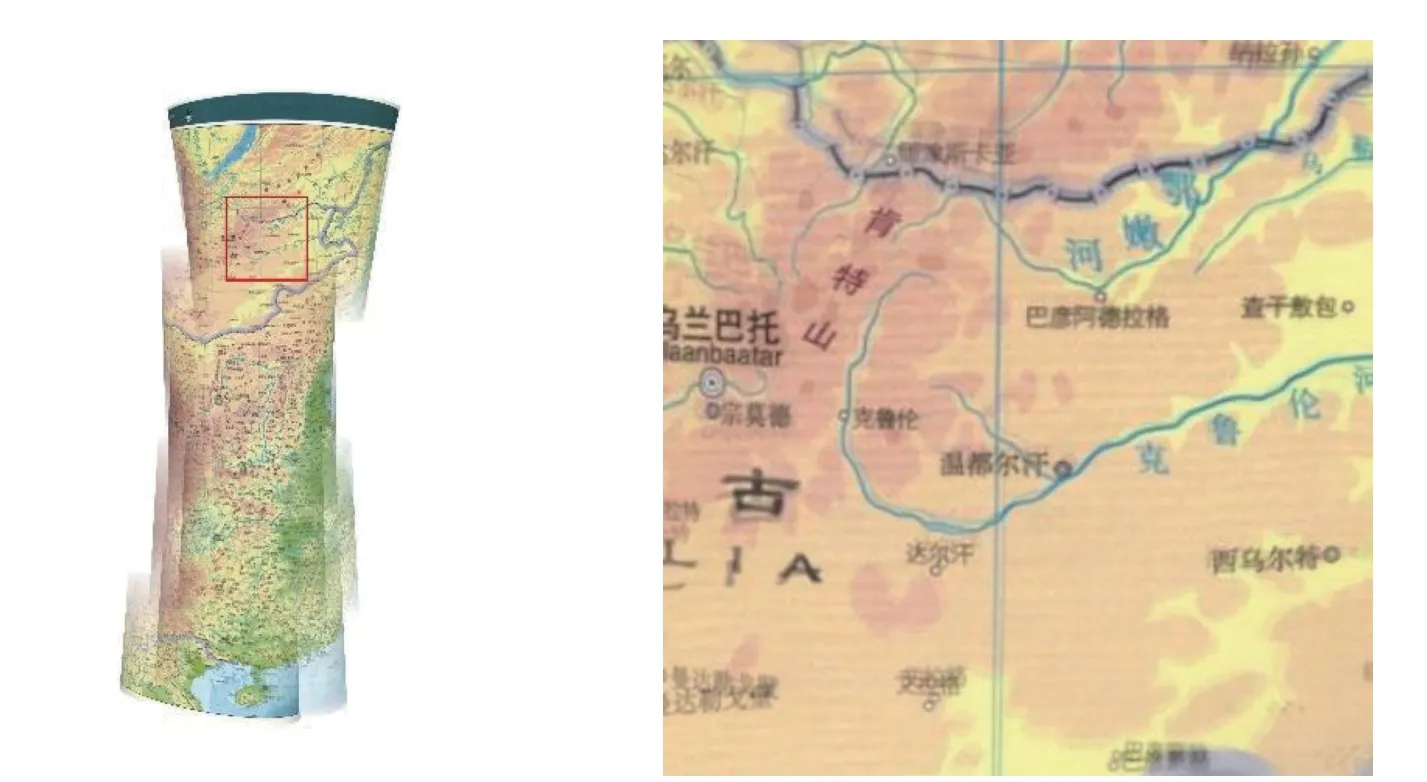
图15 OpenPano 算法在图像集A 的子集上生成的全景图Fig.15 Panorama generated by OpenPano algorithm on a subset of image set A
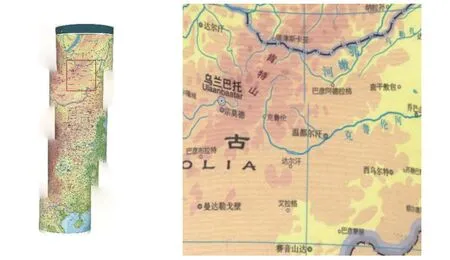
图16 PhotoShop 算法在图像集A 的子集上生成的全景图Fig.16 Panorama generated by Photoshop algorithm on a subset of image set A
从图15、图16和图17 可以明显看出,地图上的经线在PhotoShop 计算出的结果图中出现了断裂.这说明 PhotoShop 算法对线条的拼接效果不太理想;而在OpenPano 的结果图中,该条经线被较好地拼接上了,但是在线段下部出现了重影现象.图17 的左边是由CPG 生成的全景图,右边是左图上红色区域的放大图.从图17 可以看出,该条经线连接正常,也没有出现重影.
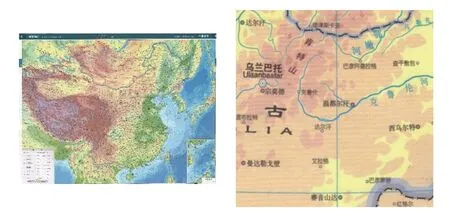
图17 CPG 算法生成的全景图的局部放大图Fig.17 Partial enlargement of panorama generated by CPG algorithm
表1 所示是图像集A 在4 种算法中的结果对比.由表1 对比结果可知,在复原完整性、拼接处痕迹、图像变形、图像重影、图像模糊和色差这6 项评估指标上,CPG 算法表现最佳;此外,在算法运算的时间复杂度中,由于其余方法无法重建出完整的全景图,因而本实验中时间复杂度不具有可比性.表1 中:“复原完整性”是指算法对图像集中所有图像复原的程度;“拼接处痕迹”评价的是相邻图像拼接处是否存在点或线未对齐的情况;“图像变形”是指图像是否存在透视现象或者扭曲的情况;“图像重影”是指图像是否存在纹理重复的情况;“图像模糊”指图像是否存在不清晰的情况;“色差”是指不同图像间是否存在色彩变化.

表1 图像集A 在4 种算法中的结果对比Tab.1 Comparison of results from image set A with four algorithms
3.3 基于图像集B 的评估实验
本实验在图像集B 上分别运行和考察了CPG 算法、OpenCV 算法、OpenPano 算法和PhotoShop算法,目的是考察这些算法对实际类柱面上的纹理进行三维拼接和全景图展开的效果.
图18是运行CPG 算法所生成的三维图像.从该图可以看到,CPG 算法可以完整地重构出洞窟壁画的三维形状和原始纹理.

图18 由CPG 算法对图像集B 进行重建后的三维图像 (3 个不同角度的截图)Fig.18 3D image reconstructed by CPG algorithm from image set B (screenshots from three different angles)
图19 为OpenCV 算法的运行结果.从该图可以看到,OpenCV 算法没能生成出完整的全景图像,有些区域丢失了;从其右图(左图红色矩形框的放大图)上可以看到,图像在拼接处没有拼接痕迹,但有一些弯曲变形.

图19 OpenCV 算法在图像集B 上生成的全景图Fig.19 Panorama generated by OpenCV algorithm on image set B
图20 为OpenPano 算法的运行结果.从该图可以看到,OpenPano 算法没能生成出完整的全景图像,只生成了与OpenCV 算法相同的区域块;从其右图(左图红色矩形框的放大图)上可以看到,图像在拼接处没有拼接痕迹,但有些地方出现了重影和模糊的情况.
图21 为PhotoShop 算法的拼接结果.从该图可以看到,很明显地在拼接处有严重的色差;从其右图(左图红色矩形的放大图)上可以看到,有些地方拼接处是错位的.

图21 PhotoShop 算法在图像集B 上生成的全景图Fig.21 Panorama generated by PhotoShop algorithm on image set B
图22 为CPG 算法的运行结果.从该图可以看到,CPG 算法能较完整地生成全景图;从其右图(左图红色矩形的放大图)上看不出图像拼接痕迹,整体颜色自然,同时也看不出有变形的地方.
表2 所示是图像集B 在4 种算法中的结果对比.表2 所示的6 项评估内容更能直观地发现,在图像变形对比中,CPG 算法在其他算法都发生透视变形时,依旧能够计算出无变形的全景图结果.从时间复杂度上可以看到,CPG 算法花费了较多的时间,但以时间为代价还原了更为完整的内容.
3.4 基于图像集C 的评估实验
本节实验是在图像集C 上进行的.图像集C是新疆克孜尔新1 窟–后室的顶部区域,该区域特点是呈半圆柱面形状分布,但又很近似于平面,并且大约有1/4 的缺损,具体如图8(c)所示.

图22 CPG 算法在图像集B 上生成的全景图Fig.22 Panorama generated by CPG algorithm on image set B
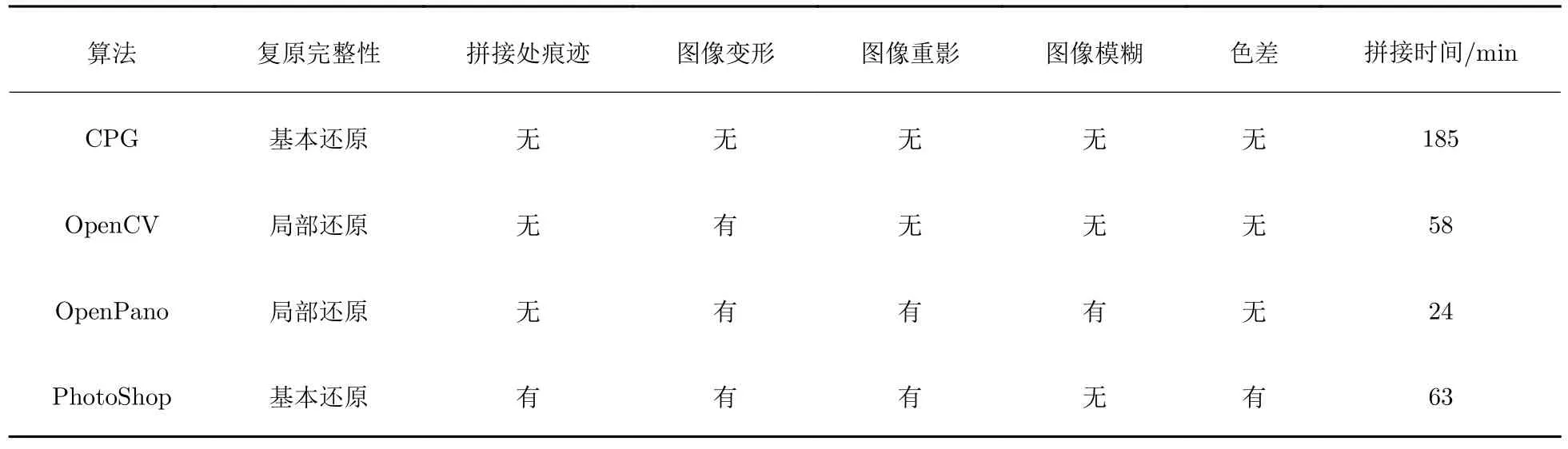
表2 图像集B 在4 种算法中的结果对比Tab.2 Comparison of results from image set B with four algorithms
本实验在图像集C 上分别运行和考察了CPG 算法、OpenCV 算法、OpenPano 算法和PhotoShop算法,目的是考察这些算法对实际类柱面上的纹理进行三维拼接和全景图展开的效果.
图23是运行CPG 算法所生成的三维图像.从该图可以看到,CPG 算法可以完整地重构出洞窟壁画的三维形状和原始纹理.

图23 由CPG 算法对图像集C 进行重建后的三维图像 (3 个不同角度的截图)Fig.23 3D image reconstructed by CPG algorithm from image set C (screenshots from three different angles)
图24 为OpenCV 算法的运行结果.从该图可以看到,OpenCV 算法没能生成出完整的全景图像,只有1/3 的区域被生成,同时有较大区域被丢失了,且全景图像的右上角存在透视变形现象.
图25 为OpenPano 算法的拼接结果.从该图可以看到,也只有1/3 区域被成功生成;从其右图(左图红色矩形的放大图)可以看到,拼接图出现了模糊现象.

图24 OpenCV 算法在图像集C 上生成的全景图Fig.24 Panorama generated by OpenCV algorithm on image set C

图25 OpenPano 算法在图像集C 上生成的全景图Fig.25 Panorama generated by OpenPano algorithm on image set C
图26 为PhotoShop 算法的拼接结果.从该图可以看到有透视变形;从其右图(左图红色矩形的放大图)可以看到,人物脸部和饰品处出现了拼接错位现象.

图26 PhotoShop 算法在图像集C 上生成的全景图Fig.26 Panorama generated by PhotoShop algorithm on image set C
图27 为CPG 算法的运行结果.从该图可以看到,CPG 算法较完整地生成了全景图;从其右图(左图红色矩形的放大图)上看不出图像拼接痕迹,整体颜色自然,同时也看不出有变形的地方.

图27 CPG 算法在图像集C 上生成的全景图Fig.27 Panorama generated by CPG algorithm on image set C
表3 所示为图像集C 在4 种算法中的结果对比.由表3 可以发现,CPG 算法在其他算法的6 项评估指标各自出现不足的情况下,依旧表现稳定,具有较高的鲁棒性;其复原完整性最高并透视扭曲最小,以时间复杂度为代价提高了拼接准确度,保证了全景图的最大程度拼接结果.

表3 图像集C 在4 种算法中的结果对比Tab.3 Comparison of results from image set C with four algorithms
3.5 基于图像集D 的评估实验
本实验在图像集D 上分别运行和考察了CPG 算法、OpenCV 算法、OpenPano 算法和PhotoShop算法,目的是考察这些算法对实际类柱面上的纹理进行三维拼接和全景图展开效果.
图28是运行CPG 算法所生成的三维图像.从该图中可以看到半圆柱面的形状,且其结构与图8 (d)的结构相同;三维图的边缘部分由于采集时洞窟的残损而造成了不规则的残缺.

图28 由CPG 算法对图像集D 进行重建后的三维图像 (3 个不同角度的截图)Fig.28 3D image reconstructed by CPG algorithm from image set D (screenshots from three different angles)
图29 为OpenCV 算法的运行结果.从该图可以看到,拼接比较自然也无色差,全景图的透视变形现象不明显,但所生成的拼接结果不完整,有较大的残缺.

图29 OpenCV 算法在图像集D 上生成的全景图Fig.29 Panorama generated by OpenCV algorithm on image set D
图30 为OpenPano 算法的拼接结果.从该图右边放大图可以发现,模糊现象较为严重.

图30 OpenPano 算法在图像集D 上生成的全景图Fig.30 Panorama generated by OpenPano algorithm on image set D
图31 为PhotoShop 算法的拼接结果.从该图右边放大图可以发现,没有明显的拼接痕迹,但是在拼接处有明显的色差,从整体上看透视现象较为明显.

图31 PhotoShop 算法在图像集D 上生成的全景图Fig.31 Panorama generated by PhotoShop algorithm on image set D
图32 为CPG 算法的运行结果.从该图可以看到较完整地生成了全景图,且从其右边放大图上看不出图像拼接痕迹,整体颜色自然,也看不出有变形的地方.

图32 CPG 算法在图像集D 上生成的全景图Fig.32 Panorama generated by CPG algorithm on image set D
表4 所示为图像集D 在4 种算法中的结果对比.由表4 可以发现,在该数据集上,CPG 算法依旧在图像变形这一评估内容上具有较高的水准.对于多平面的柱面图像拼接任务,CPG 算法具有能基本还原纹理、无变形、无重影、无模糊和无色差的优势;OpenCV 算法与OpenPano 算法都只拼接出了部分内容;PhotoShop 算法虽拼接出了全部内容,但其透视效果严重.在本实验中,CPG 算法的时间消耗较为优势.这是由于图像集的三维形状更接近于理想圆柱面,因而减少了计算圆柱面参数所耗费的时间;而OpenCV 算法与OpenPano 算法的处理更接近于圆柱面的拼接对象的拼接时,在图像对准上会消耗更多的时间.

表4 图像集D 在4 种算法中的结果对比Tab.4 Comparison of results from image set D with four algorithms
4 结论
本文提出了一种对非规则圆柱面壁画比较有效的全景图像生成方法.该方法首先依据采样图像集重建出三维模型,使得分网格拍摄的图像在三维空间进行拼接和融合;然后把三维非规则圆柱面拟合到1 个理想圆柱面上;最后把理想圆柱面展开成全景图像.通过实际洞窟图像集的实验,验证了本文所提CPG 算法具有一定的实用性.但是CPG 算法对于图像边缘区域的处理性能和整体的处理速度略有不足,提高CPG 算法在这两个方面的表现是后续将研究的课题.
