基于视觉神经元PID的AGV轨迹跟踪控制器*

李魏魏，袁 森，周小容

(1.贵州大学机械工程学院，贵阳 550025；2.贵州理工学院机械工程学院，贵阳 550003)

0 引言

近些年来，随着计算机技术和图像处理技术的发展,基于视觉导航和智能控制的自动引导车成为人们研究的热点[1-2]。由于AGV航迹控制系统是时变的非线性复杂系统，作业过程中容易受到外来不可预测的因素干扰，致使AGV不能按预设路径行驶[3]，因此纠偏系统的研究至关重要。

控制AGV模式中，相比采用超声波、激光、等引导方式的AGV模型,采用视觉传感器引导的AGV具有响应速度快、成本低、获取信息量大的优势[4]。王荣本等[5]采用机器视觉获得导航参数,利用线性最优控制理论得出固定反馈增益来实现对导航路径的跟踪。该控制器对于较小角度的转向控制有一定的优越性,但没有讨论在较大偏差情况下的控制问题。谭建豪等[6]改进生物启发神经动力学模型算法，提高了神经元决策的精准性和信息有效性，但未讨论信息输入神经元需要不同的神经元接受。罗哉等[7]提出了一种基于最优偏差路径的模糊PID纠偏算法，利用实时调节驱动轮的差速消除航向偏差，误差发生较大跳变时PID难以收到良好的效果。武星等[8]针对AGV导引路径的精确跟踪问题，提出一种导引扫描窗口设置方法，但却没有考虑设备安装的误差、光线灰暗、车身抖动等导致采集误差。苗静静等[9]针对磁导航自动导引车的路径跟踪问题，以前轮舵机转向、后轮电机差速驱动型AGV为研究对象,使前轮配合后轮转向运动，提高路径跟踪精度,若后轮产生误差会使前轮偏差放大。陈显宝等[10]为了提高AGV的定位精度，在融合视觉图像精确定位、快速识别的特性基础上，设计了基于DM码的AGV视觉二次定位算法。但是该方法提高定位精确度的前提是要求AGV导航系统一次定位的精度可以达到(±20 mm，±20 mm，±2°)以内。尹晓红等[11]在神经动力学模型中讨论神经元内部信道的过程，提高了人工神经元的真实性和信息处理的准确性，但却忽视了神经元在传递决策过程中信息的有效性和处理信息的快慢。

综上所述，对于AGV路迹跟踪的研究成果颇多，但路径跟踪精度始终不能够达到预想结果，且有诸多前提条件限制下提高精度高。因此本文将采用AGV的两个驱动轮差速作为控制转向，结合视觉神经元PID纠偏路径控制算法，将图像数字化数据和传感器辅助数据作为神经元调速系统的输入量，优化的输出数据通过双通道PID对纠偏电压精准控制无刷直流电机的差速实现提高AGV的路径跟踪精度。

1 图像数字化与辅助数据

1.1 图像数字化

采用单目视觉摄像方式，采集到的图片以矩阵的形式表达出来，如图1所示，坐标系OC为相机坐标系，且ooC为相机设备的焦距f，x轴方向上感光芯片单位像素的实际大小为dx，在y轴上单位像素的实际大小为dy，右上角为世界坐标系，故可以用(xw，yw，zw)表示三维空间中的真实坐标点。

图1 相机坐标系与世界坐标系

设rw=[r1r2r3]是相机坐标系相对于世界坐标系的旋转矩阵，其中r1=[r11r12r13]T、r2=[r21r22r23]T、r3=[r31r32r33]T分别为x轴、y轴和z轴的旋转矩阵，设T=[txtytz]T其中tx、ty、tz分别是x、y、z轴的平移向量。可以得到世界坐标系与像素坐标系的关系式为：

(1)

式中，u、v轴分别对应图像坐标系中的x、y轴；坐标(u0、v0)为图像坐标系中图像中心位置点，则可以得出世界坐标系和图像坐标系的互换关系：

(2)

式(2)是摄影测量学中的共线方程,这也是针孔模型或者中心投影的数学表达式[12]。在摄影机内部参数R、T、f确定的情况下，可以利用图像坐标系的像点和对应的物点，结合式(2)可以求解出对应的世界坐标。

1.2 辅助数据

视觉导引AGV的系统误差主要来自两个方面，即设备安装、光线灰暗、车身抖动导致的误差[13]。为确保AGV小车精准的在预想路径上行驶，图像分析的数据难免会有误差，因此添加精确辅助数据-西克传感器。预先用与传感器对应的感应纸铺设一条预计路径，感应线能被传感器所检测不受光线所影响，其原理如图2所示。

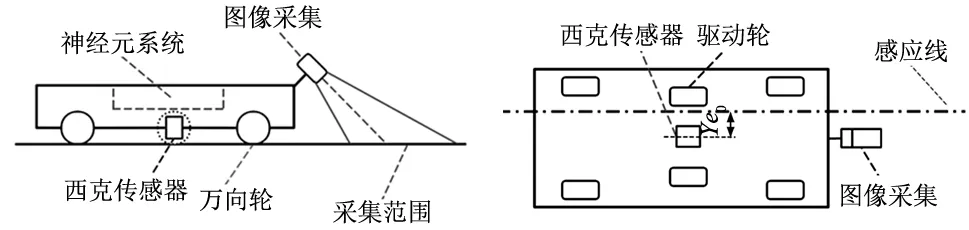
图2 AGV路径纠偏示意图

在图2左图中，图像采集模块利用感应线可以识别地标位置，实现AGV行驶过程中可以实时监控和查看小车所处的准确位置。因车身抖动，光线昏暗等，使得采集图片不理想导致数据不精确，因此采用西克传感器精准辅助数据，得到准确有效的优良数据。

图2右图中西克传感器可以准确测量AGV几何中心与感应线之间的垂直距离，从图中能够看出该传感器可以得到AGV几何中心P与感应纸中心线p0的横向偏距Ye0，使得神经元控制器改变驱动电机的电压大小，从而形成驱动轮的速度差，可以纠偏行驶过程中产生的误差，但这种误差要对AGV进行运动学模型的建立，得出所存在的位姿误差。

2 AGV视觉神经元系统

2.1 AGV位姿误差模型

为了使模型具有一般性，假设AGV车身为刚体，没有任何形变；地面水平且与驱动轮之间无任何摩擦，可以将AGV的质心p1视为始终落在几何中心处[14]，模型如图3所示。

图3 AGV运动学模型

图3中，xw1、yw1和θ分别表示为车体中心坐标和车体方位角，则可用p1=(xw1,yw1,θ1)T表示AGV的一个位姿，p2=(xw2,yw2,θ2)T表示为参考误差位姿；其中VE、VF表示驱动轮E、F的前进线速度，ω表示为车体的角速度，对应的速度矩阵Q=(VE,VF,ω)T；L1、L2、L3分别为AB之间的轮距、BC前后轮之间的轴距、EF之间的轮距。

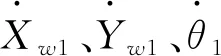
(3)

如图3所示内的p2为参考误差位姿，其在坐标内描述的位姿误差e表示为：

(4)

假设此时误差位姿p2对应的两驱动轮E、F的前进线速度分别为VE2、VF2。故对上式位姿误差e求微分，所得结果为：

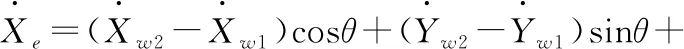
(5)

同理可得：

(6)

(7)

综合式(5)～式(7)式可以得出AGV位姿误差动力学数学模型：

(8)

2.2 视觉神经元动态分析

目前已经有很多关于生物神经元的研究，应用最为广泛的是在H-H模型基础之上提出的分流模型(shunting modle)[15]。

(9)

工业控制中PID是应用最为广泛的一种控制器，但在参数变化大、数据突变的工业领域中，PID的控制鲁棒性能不高。鉴于考虑到动态神经元模型具有稳定、增益自调整和输出光滑且有界等优良的特性[13]，本文利用生物激励神经网络解决PID在控制领域所存在的不足。

电信号变化是神经元之间活动的一种重要体现，但目前人工神经元大部分不考虑内部的传送信息机制，导致有些生物神经元的优良特性缺失。为更好的模拟出生物神经元，考虑信息传递和择优传递过程，如图4所示神经动力学门限偶极子模型[16]，它有两个对立的信道：on和off，其中on信道接收来自目标和相邻神经元的激励信号J，off信道接收一个外部抑制输入信号K，两个信道都接收唤醒信号I。

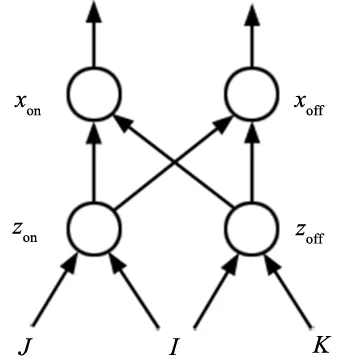
图4 门限偶极子模型

on和off细胞上的信号分别来自zon、zoff其动态特性为：

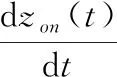
(10)

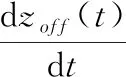
(11)

式中，参数α、β和γ均为正常数；α和γ分别为变送器的生成率和损耗率；β为变送器的总数量；信号I、J和K分别为：

(12)

(13)

Ki=[Ii]-

(14)

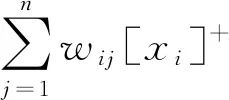
图5 神经网络单元

图5中可以看出每一个神经元之间的传递方向和长度不一样，即每一个神经元做出决策的偏移方向将会影响数据信息的有效性和响应时间，因此考虑兴奋信号和抑制信号的传递延迟。综合以上分析和受神经元动力学模型启发，神经网络中的第i个神经元的动态算法xi可表示为：

(15)

式中，η为任意模拟时间单位的时间步的大小；τ为神经元传递延迟率；上式中在经典神经动力学模型方程基础上增加了对下一节点决策选择影响因子：dijsina、dijcosa，根据图5所示神经元的位置关系，其分析如图6所示。

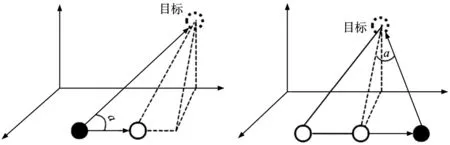
(a) si到sj的激励信号输入 (b) sj到si的抑制信号输入

图6a中，∠a为决策相对目标的偏移方向。故在输入PID控制器之前，把视觉参数化信息输入到改进神经动力学模型中，使得产生的是有界光滑、柔和的视觉神经元信号。

3 纠偏控制器系统设计

3.1 无刷直流电机数学模型

无刷直流电机数学模型可以描述为[18]：

(16)

式中，Uw为定子绕组相电压；Rs为定子绕组相电阻；I为定子绕组电流；E为定子绕组反电动势；Lw为定子绕组的电自感；Lww分别为定子绕组之间的电互感。把整个无刷直流电机视为一个整体，对式(16)进行化简结合，可以得到无刷直流电机数学模型：

(17)

式中，U、i分别为电机两端电压、电流；R为定子电阻；L为定子电感；k为反电动势系数；ω为电机角速度。

3.2 纠偏路径控制算法

差速转向式AGV的纠偏轨迹是多个不同半径和瞬心的圆弧运动的组合，利用E、F轮的速度差来控制AGV的精准路线，速度的实时精确控制至关重要。由此控制系统采用转速-电流双闭环直流控制，转速闭环采用神经元PID控制器，既保证了系统的稳定性，又能实现速度的精确性。

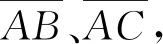
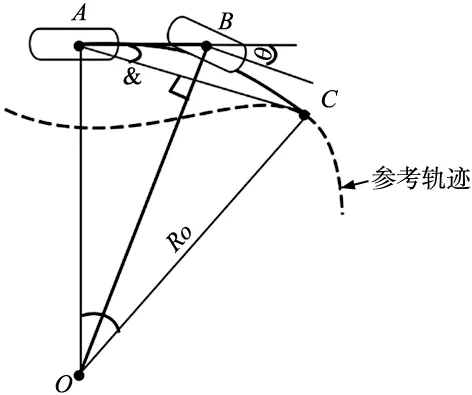
图7 实际运动轨迹误差纠正运动学模型

根据弦切角定理可知；∠AOC=2∠BAC=2&，为了使小车沿着圆弧运动准确到达C点，在ΔAOC中需要满足的关系式为：

(18)

B点所处位姿与A点位姿的夹角为θ，故可得：

(19)

假设无刷直流电机到驱动轮之间传动比为β，故可得：

θ(t)=λβΔωr×t

(20)

把式(17)无刷直流电机数学模型积分可得：

ΔUt=Li+Rit+kΔωt

(21)

联立式(20)、式(21)可以得到：

(22)

(23)

式中，r为E、F驱动轮的半径，得出AGV的偏差数据与纠偏电压的关系式。把上面描述的偏差数据和纠偏电压的控制算法编程到神经元系统。

纠偏控制算法是AGV偏航数据对无刷直流电机角速度的控制，考虑PID的单一方向性，大小相同正负性不同的误差作为输入信号，PID控制器对无刷直流电机的控制电压大小是一样的。由于纠偏电压ΔU调速存在正负两个方向的控制，可以将电压差视为两个不同的控制领域。因此采用双通道PID控制，不断调整PID的参数实现夹逼准则以达到实现目标数值。

结合前面的位姿误差动力学数学模型、神经元动态分析、转速调节控制方法，可以得出视觉神经元控制系统如图8所示。

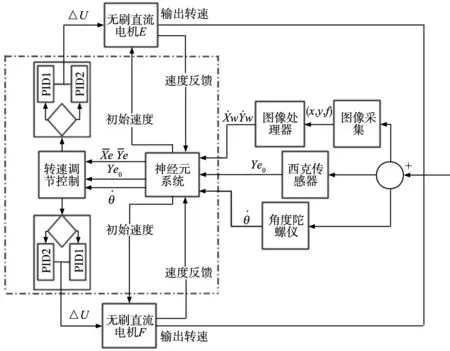
图8 基于视觉神经元PID轨迹跟踪控制器原理图

4 仿真计算与结果分析

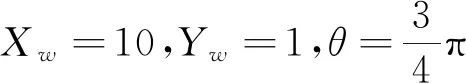
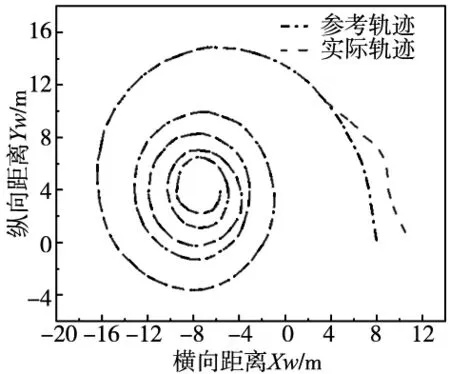
(a) 路径跟踪

设计U型参考轨迹，AGV的初始速度为VE=VF= 1.1 m/s，车身旋转角速度ω=0 rad，设置初始位姿Xw=1，Yw=1，θ=0 rad。参考运动轨迹为螺旋曲线时，如图10所示。

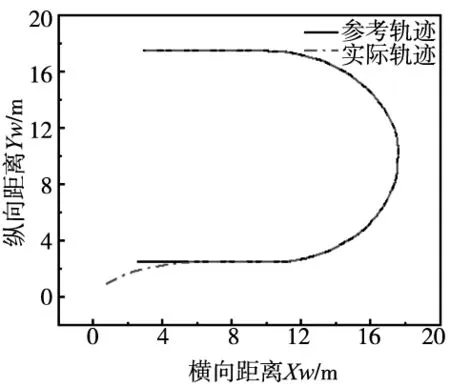
(a) 路径跟踪

用一般的PID控制方法与视觉神经元算法进行螺旋曲线轨迹对比，参考估计和初始位置与视觉神经元算法相同，仿真结果如图11所示。

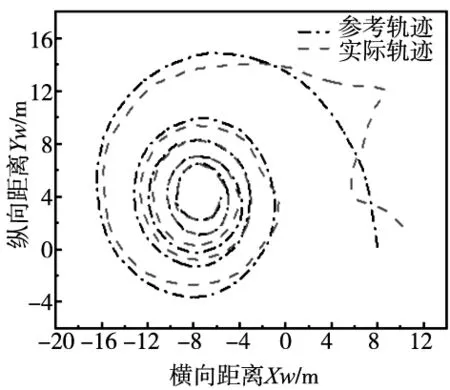
(a) 路径跟踪

再结合PID路径控制算法进行U型曲线比较，参考轨迹和初始位置与视觉神经元算法相同，仿真结果如图12所示。

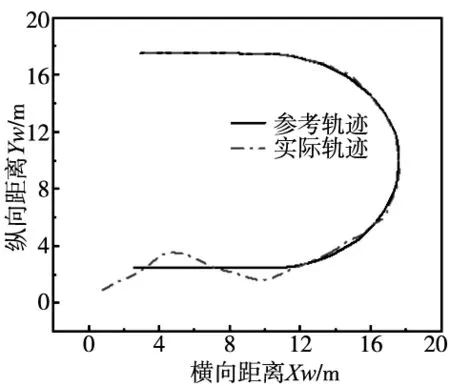
(a) 路径跟踪

在图9a和图11a中，设计的视觉神经元PID纠偏路径控制算法使得初始速度突问题和速度稳定性得以解决，在轨迹跟踪精确度方面效果也很好，PID控制相对来说轨迹跟踪效果不太好。图9b中，小车只需4 s左右就可逐渐将误差控制在(-1.5，1.7) mm；图11b却需要要15 s才能逐渐将误差控制在(-2.2,2.5) mm范围内，尤其姿态误差角，视觉神经元PID纠偏路径控制算法基本维持在零范围，PID控制在(-0.2，-0.5)之间；在图9c和图11c中，采用视觉神经元PID纠偏路径控制算法控制器避免了角速度的突变，没有发生激烈的振荡。无神经元控制器响应跳变过于激烈，稳定性不高，到达预设值的时间滞后。

在图10和图12中，在接近参考轨迹直线段时开始分析和计时。横向偏差为1 m时，视觉神经元纠偏算法回归到参考轨迹用时4 s左右,而PID路径纠偏算法控制器用时15 s左右，提高用时效率30%左右；在图12中，PID路径纠偏控制算法比较稳定光滑，这是因为利用该算法可以寻迹出最优路径，到导航轨迹点后，将该点作为当前位置，然后继续使用路径纠偏控制算法寻找下一时刻的导航轨迹点，反复执行路径纠偏控制算法决策过程，直到抵达目标点。下一步的研究重点是将所设计的视觉神经元PID纠偏路径控制算法运用到AGV实物中，进行实验验证。

5 结论

此研究提出一种基于视觉神经元PID的AGV轨迹跟踪控制器，分析了图像预处理和提出视觉神经元控制算法；结合无刷直流电机的数学模型和AGV运动误差数学关系式推导出纠偏路径控制算法；结合两种算法得到视觉神经元PID纠偏路径控制算法。最后分析视觉神经元PID纠偏路径控制算法分别对比普通PID在螺旋轨迹上、PID路径纠偏控制算法在U型轨迹上的位姿误差和角速度随时间变化的仿真结果，得到以下结论。

(1)采用视觉神经元PID纠偏路径控制算法跟踪控制器的AGV，回归到参考轨迹用时4 s左右，而一般PID控制器用时15 s左右，提高用时效率30%左右。在参考轨迹上运行时神经元控制器的AGV误差保持在(-1.5，1.7) mm，无神经元控制器AGV其误差保持在(-2.2，2.5) mm，误差率减小68%左右。

(2)路径纠偏控制算法利用无限分割曲线路径原理，寻迹出最优路径，可以提高AGV导航轨迹跟踪精度。

(3)视觉神经元PID纠偏路径控制算法比PID纠偏路径控制算法更能有效避免了角速度的突变。