能耗优化的改进IWOA-APF移动机器人路径规划*

张 品，李长勇

(新疆大学机械工程学院，乌鲁木齐 830017)

0 引言

近年来，快速发展的机器人[1]被应用到不同场景，如生产制造[2]、物流仓储[3]、应急救援[4]等，而路径规划是机器人自主导航的核心技术。在机器人导航中，路径指标固然重要，也要尽量降低机器人的能耗，增加机器人的工作时间。

李文刚等[5]用堆结构优化了A*算法列表，将DWA算法和A*算法结合，解决了多种障碍物的避障问题，保证了路径平滑。殷绍伟等[6]通过考虑活跃度等信息改进了转移概率函数，基于不平等原则更新信息素，加快了算法收敛。迟胜凯等[7]通过生成最小子数获得初始路径，考虑了移动障碍对代价势场的影响，对移动障碍物达到较好的响应效果。陈艺文等[8]通过挪移处理使路径点远离障碍物，利用混合A*对路径进行再规划，提高了安全距离。李海等[9]通过空间凸分解和改进区间分配策略，规划出了快速、安全的路径。HOSSEININEJAD等[10]选择机器人到目标点连线上的动态点作为特征向量，每一步规划运行一次COA算法，直至到达目标点。GERMI等[11]根据障碍物动力学原理，通过加入项修正了负场，使用改进遗传算法在线调节所需系数，提高了规划能力。YONG等[12]通过计算路径的置信度，生成由置信度控制的树形图，最后采用剔除的方法生成了优化路径。常规方法存在路径曲折，转角过大，路径评价指标单一，未考虑能耗等问题。

本文提出一种考虑能耗的IWOA-APF机器人路径规划方法。建立机器人能耗模型，分析人工势场法的常见弊端，通过设置横向扰动力，转角限制系数促使机器人逃离死点和圆滑路径，对C类障碍采取填充，避免无效路径。利用混沌映射、bezier型收敛因子、自调节权重因子改进鲸鱼算法，利用IWOA优化势场引力和斥力系数，最终规划出能耗少，规划快的平滑路径。

1 机器人运动学模型与能耗模型

1.1 机器人运动学模型

为了方便建模，设定机器人轮子与地面不产生滑动，且机器人质量分布均匀。同时四轮机器人可以简化为两轮差速模型，模型的状态变量为X=[vxωz]T，控制变量为U=[ωlωr]T。机器人的线速度为R(ωl+ωr)/2，角速度为R(ωr-ωl)/H，可得运动学模型为式(1)，运动示意图如图1所示。

图1 运动示意图

(1)

式中，vx为机器人线速度，m/s；ωz为机器人角速度，rad/s；ωl为机器人左轮转速，rad/s；ωr为机器人右轮转速，rad/s；R为机器人轮径，m；H为机器人宽度，m。

1.2 机器人能耗模型

为了提高机器人的工作时间，建立机器人能耗模型，将能耗指标量化，减少机器人的非工作能量消耗。因为机器人的移动速度较低，而且四轮驱动抓地有力，所以风阻和纵向摩擦设定为0，则机器人的非工作能耗主要由电池内耗、电机损耗、横向摩擦损耗[13]三部分组成。

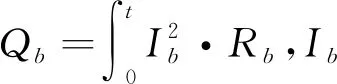
而轮胎侧偏角和机器人转角呈相关关系，故可得出非工作耗能为：

(2)

式中，c为轮胎侧偏角和机器人转角相关系数；θ为机器人转角。

通过能耗公式可以得出，通过提高路径规划效率，降低工作时间，可以减少Qb、Qm，在规划时降低总转角，可以提高效率和降低能耗，从而降低非工作能耗。

2 人工势场法分析与改进

2.1 原始人工势场法

APF的机理是将周围的环境转换为势场模型，目标点产生引力场，障碍物产生斥力场，目标点和障碍物对机器人作用的合力控制机器人运动方向。势场通过引力系数和斥力系数调节，负梯度方向为势场值变化最大方向。故引力场和引力函数为：

(3)

式中，ka为引力系数；X为机器人位置；Xg为目标点位置。斥力场和斥力函数为：

(4)

式中，kr为斥力系数；ρ为机器人到障碍物距离；ρ0为障碍物影响距离。

由于机器人位置的不断变化，导致所受合力方向的不断变化，在沿着长条形、C型障碍物规划路径或者通过狭窄通道时会产生路径抖动现象，在合力为0时会产生死点。

2.2 改进人工势场法

针对死点情况，设置横向扰动力，扰动力设置规则为，方向在机器人到目标的连线偏转一定角度，大小为和目标点引力相等。对于C类障碍物，其内部路径无效，对C类障碍物填充处理。由式(2)可知，机器人总转角影响能耗，在死点或者特殊情形障碍物附近，会出现路径抖动问题。因此给机器人规划路径过程中增加角度限制。角度限制系数定义为：

(5)

式中，l为限制系数；h为机器人到障碍物的距离；ρ0为障碍物影响范围。

由图2可以看出，增加了横向扰动力以后，机器人可以逃离单障碍死点，长条形障碍，C型障碍，完成到目标点的规划。在对C类障碍填充处理后，机器人路径和转角减小，则减小了非工作能耗。

在规划路径时，引力系数ka和斥力系数kr是APF的重要参数，通过改进的鲸鱼算法实时调节ka和kr，可以进一步优化路径。

3 鲸鱼算法

3.1 基本鲸鱼算法

鲸鱼算法[14]仿照座头鲸种群的捕食行为，在寻优空间内，每一个座头鲸都是解。寻优过程从随机解开始，根据bubble-net捕食策略更新目前最优解。鲸鱼算法和灰狼算法等类似，均通过围捕猎物觅食。鲸鱼通过吐出气泡形成螺旋形捕猎陷阱，由于最优猎物群的位置是未知的，通常设置当前最优猎物为目标猎物。其他的座头鲸通过不断迭代更新自己的位置。围猎行为可以表达为：

(6)

式中，D是座头鲸和最优鱼物群的距离；t是当前代数；A、D是系数；X*(t)是当前最优鱼群位置；X(t)是座头鲸当前位置。其中系数的计算公式为：

A=2a·r-aC=2·r

(7)

式中，r∈[0,1]为随机数；a在迭代过程中，线性从2递减到0。

包围猎物后，座头鲸会发出螺旋形的泡泡网攻击鱼群，通过减少a的值来向鱼群收缩，A的扰动范围为[-a,a]。由机理可知，更新位置后的座头鲸处于目前位置和目前最优鱼群之间。座头鲸的攻击行为：

X(t+1)=|X*(t)-X(t)|·eml·cos(2πl)+X*(t)

(8)

式中，m为设置螺旋线性的常数；l∈[-1,1]为随机数。

座头鲸在捕猎时，同时进行发出螺旋攻击气泡和收缩包围圈的运动。这两种运动的概率相同，可以表示为：

(9)

除了气泡攻击，座头鲸也会依据其他非最优鲸鱼位置随机搜寻鱼群，这个策略使得WOA具有全局搜索能力，随机搜寻行为表示为：

D=|C·Xrand-X|X(t+1)=Xrand-A·D

(10)

式中，Xrand为随机选择的鲸鱼位置。

3.2 改进鲸鱼算法

在初始化座头鲸群时，采用Chebyshev混沌映射初始化座头鲸群，混沌映射具有随机性、遍历性，能够使初始解遍布捕猎空间。Chebyshev映射的公式为：

xk+1=cos(k·cos-1(xk))

(11)

鲸鱼算法寻优过程中，由于a是在[0,2]中线性递减，不能适应实际的寻优过程。提出一种bezier型收敛因子，bezier曲线通过确定端点可以生成圆弧类曲线，改进后的bezier型a的取值和变化如图3a所示。

(12)

在座头鲸群更新位置过程中，加入权重因子，动态调整某个座头鲸的权重。权重因子w公式和变化图如式(13)和图3b所示。

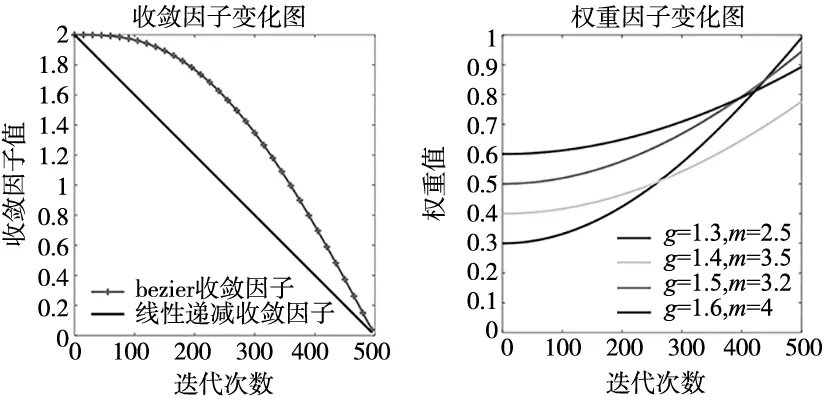
(a) 收敛因子变化图 (b) 权重因子变化图

(13)

式中，g、m为调节系数，g值调整权重因子曲线的起点值，m值调整曲线的弯曲程度。通过对不同g、m参数的实验，得出当g=1.3、m=2.5时，权重因子w使算法各项性能均衡、优质。

改进后的座头鲸位置更新公式为：

(14)

4 仿真实验及结果分析

4.1 算法流程示意

改进后的IWOA-APF算法流程如图4所示。

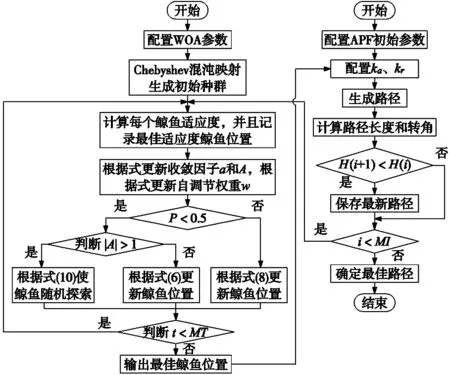
图4 IWOA-APF算法流程图

4.2 测试结果与分析

选取经典三种基准函数对改进鲸鱼算法进行仿真测试，分别为单峰测试函数、多模态测试函数、固定维度多模态测试函数。用MATLAB软件进行仿真,设定算法的迭代次数为500次；种群数量为30；选取近年新型群智算法，在各个方向的性能进行对比分析，测试函数如表1所示。

表1 测试函数

图5中，f1、f2为单峰测试函数。单峰测试函数最优解唯一，主要检验算法的开发能力和和收敛性。由图5a和图5b可以看出，在求解f1函数时，IWOA算法收敛很快，在前200次迭代的求解质量已远远优于其他算法。随着迭代次数的增加，IWOA不断跳出局部最优，求解质量进一步提高。求解f2时，刚开始的10次迭代，各算法差距不大，在200次以后，其他算法基本稳定，IWOA在350次进一步突破，找到更优解。

f3、f4为多模态测试函数，多峰函数主要测试算法的探索能力。由图5c和图5d可得出，求解f3函数时，在前20次迭代IWOA已经求解到更优解，在迭代100次以后各算法除GWO外基本稳定，GWO在380次迭代后有小幅度跳出。求解f4函数时，IWOA和WOA算法都明显优于其他算法，但IWOA在前50次已经求得优质解，且其他算法除GWO外收敛较慢。

f5、f6为固定维度多峰函数，主要测试求解复杂多维问题能力。由图5e和图5f可得出，求解f5时，起始阶段WOA算法快速收敛，但在25次陷入极值且不能跳出，其他算法在100次后基本稳定，且求解质量不如IWOA，IWOA算法在前30次迭代已经求得更优解。求解f6时，所有算法求解速度都较快，但到局部极值点后其他算法没有跳出，IWOA算法在60次后仍然持续跳出，求得更优解。

(a) f1求解结果 (b) f2求解结果

对改进后的IWOA-APF算法进行仿真实验，设置常见死点与路径抖动环境，比较改进IWOA-APF算法和原始APF法的求解步数和总转角。路径对比如图6所示。

图6 路径对比

由图6和表2可以得出，IWOA-APF算法的路径更短，且在通过狭窄通道处没有路径抖动现象。在经过C类障碍时，可以填充障碍物，避免无效路径，同时限制了转角，路径的求解步数和总转角都更少。

表2 算法对比

5 结论

本文针对人工势场法路径规划的局限问题，提出了一种能耗优化的改进IWOA-APF机器人路径规划方法。设置了横向扰动力和转角限制系数克服死点和抖动，对C类障碍填充处理。利用权重因子等策略改进了鲸鱼算法，平衡了探索和开发过程。仿真结果表明，IWOA-APF算法的求解步数更少，且总转角也更少，非工作能耗降低。

由于只在静态环境中进行了实验，本文下一步工作方向，加入动态障碍物验证算法效果，并且提出应对动态障碍的路径策略。