高速高精度伺服系统前馈参数及智能整定研究*
2022-11-25刘述进贺云波李泽声廖回隆钱其豪
刘述进,贺云波,李泽声,廖回隆,钱其豪
(广东工业大学机电工程学院,广州 510006)
0 引言
永磁同步直线电机相比于旋转电机,具有高速度、高精度和大推力的优势,在微电子封装领域有着广泛的应用。作为运动系统的关键部件,实现永磁同步直线电机的高速高精度控制,是微电子封装装备需要解决的核心问题。对直线电机的控制方法有很多,相比传统的PID控制方法,复合控制方法能够得到更好的控制效果,大量学者进行了研究。赖国庭等[1]基于PMAC的直线电机控制系统,在传统的PID控制算法的基础上再加上速度和加速度的前馈,较好地补偿了系统的跟随误差从而提高了系统的性能。侯伯杰、李万周等[2-3]在直线电机伺服系统中使用了复合前馈PID控制方法,缩短了系统的调整时间并减小了系统的超调量,李万周提出的自适应前馈系数调节方法,使得系统具有更好的响应速度和良好的动静态特性。谭华军等[4]提出了一种伺服系统前馈反馈复合控制方法,以传统位置伺服系统传递函数模型为基础,通过设计复合控制器,为伺服系统添加了位置前馈控制器和电流环反电动势前馈补偿,有效地改善系统动态性能和跟踪精度,在阶跃和斜坡信号的作用下,均能准确地跟踪给定信号。
上述学者对直线电机的复合控制提出了各自的解决方案,有效地提高了运动系统的跟踪精度和定位精度。本研究通过前馈理论研究分析,提出“三环PID+三参数前馈”复合控制方法,采用四阶S曲线位置规划算法,在高性能运动控制卡上构建高速高精度伺服系统。针对3个前馈参数整定困难,若依靠人工整定费时费力,很难获得较优的前馈参数值,提出使用差分进化算法自动整定伺服系统中的3个前馈参数,通过对算法中个体适应度函数的设计,有偏向地优化动静态段的运动效果,满足运动系统不同运动场景的要求。
1 高速高精度伺服系统构建
1.1 “三环PID+三参数前馈”复合控制结构
传统PID控制属于反馈控制,是一种有差调节,如果只使用反馈控制,会影响系统的轨迹跟踪性能。在高速高精度运动控制中,为了实现更好的轨迹跟踪,需要引入前馈控制器,通常由理想轨迹信号与前馈控制器相结合,产生前馈控制信号,实现系统的快速响应和高精度位置跟踪。
在采用“反馈+前馈”控制策略时,忽略扰动w(t)的影响,系统输出Y(s)对输入R(s)的传递函数为:
(1)
系统误差E(s)=R(s)-Y(s),代入式(1)中,得到系统误差对输入的传递函数为:
(2)
当跟踪误差E(s)为0,Gff(s)=1/G(s)时,理论上可以实现输入轨迹的完全跟踪(不变性原理)。引入前馈控制前后系统传递函数的特征方程不变,故引入前馈控制不会改变系统的稳定性,却可以在不改变原系统参数和结构的情况下,大大提高系统的稳态精度,动态性能也比较容易得到保证[5]。
永磁同步直线电动机伺服系统具有复杂耦合性和各部件参数测量难度大、不精确等特点,基于理论模型与真实模型具有一定差异[7]。有些研究通过理想假设[3-6],推导出直线电机的传递函数为二阶模型,前馈控制器使用速度前馈和加速度前馈两个参数。考虑到将驱动器和运动平台作为控制对象,其传递函数的阶数是高于两阶次的[7]。要完全消除跟随误差,需要引入规划位置的一阶、二阶以至更高阶的导数,理想的前馈传递函数[8]为:
Gff(s)=a1s+a2s2+a3s3+…+ansn
(3)
永磁同步直线电动机伺服系统的精确数学模型是难以获取的,无法通过控制对象的数学模型来推导出前馈参数的个数和具体参数值,理论上前馈参数越多,跟踪误差越小,但是在确定前馈参数值时会花费更多的工作量,所以本研究提出使用3个前馈参数的前馈控制器,与PID控制器构成“反馈+前馈”复合控制。3个前馈参数的前馈控制器传递函数如下:
Gff(s)=a1s+a2s2+a3·s3
(4)
由于驱动器内部已独立实现了电流闭环,通过在高性能运动控制卡中构建位置速度双闭环伺服算法,实现如图2所示的“三环PID+三参数前馈”复合控制结构。

图2 “三环PID+三参数前馈”复合控制结构示意图
其中,三参数前馈控制器的公式为:
FFC(k)=ffKv·V_prf(k)+ffKa·A_prf(k)+ffKj·J_prf(k)
(5)
式中,FFC(k)为前馈控制器输出;ffKv为速度前馈系数;ffKa为加速度系数;ffKj为加加速度系数;V_prf为速度规划;A_prf为加速度规划;J_prf为加加速度规划。
1.2 高速点位运动规划设计
由式(5)可知,前馈控制器的输出与速度规划,加速度规划,加加速度规划有关。运动规划类型可分为梯形、S 曲线、三角函数型、抛物线型等等,在工程实践中,S曲线运动规划被证明是一种可以缩短定位时间并避免激发过大残余振动的有效方法[9-11]。本研究使用四阶S曲线运动规划,即四次多项式位置规划算法。这种算法计算简单,能够保证运动速度、加速度的平滑变化[12]。方程为:
(6)
含匀速段的规划曲线如图3所示。

(a) 位置规划曲线 (b) 速度规划曲线

(7)
(2)匀速段公式推导。当Vmax=Vinput,如果Sinput>2·S1(t1)条件成立,则存在匀速段,反之则不存在匀速段。当匀速段存在时,最大加速度为:
Vmax=Vinput
(8)
匀速段结束时间为:
(9)
当匀速度不存在时,t2=t1,由S1(t1)=0.5Sinput可以推到出最大加速度为:
(10)
匀速段(t1 (11) (3)减速段公式推导。根据图3,通过各阶曲线的几何关系很容易推导减速段结束时间t3=t2+t1和减速段(t2 (12) 利用上面推到的规划公式,只需要给定规划位置Sinput,最大规划速度Vinput和最大规划加速度Ainput三个值,就可以获得位置,速度,加速度,加加速度的规划曲线,各阶的规划数据构成前馈控制器的输入部分。该规划算法输入参数简单,保证了运动速度、加速度的平滑变化,可以满足高速高加速度点位运动的要求。 在伺服算法和规划算法构建完成后,需要对伺服参数进行整定,使得系统拥有良好的运动性能。本文只针对前馈参数的优化进行研究,在确定PID参数后,提出使用标准差分进化算法对3个前馈参数进行优化整定。前馈参数差分进化智能整定算法中,种群个体由3个前馈参数ffKv、ffKa、ffKj构成。初始化种群后,通过变异,交叉和选择操作产生新一代种群[13]。 图4 前馈参数差分进化智能整定流程图 个体适应度函数的设计决定差分进化算法个体进化的方向,在前馈参数差分进化智能整定算法中,个体适应度函数的设计有3个方向:①优化运动动态段的运动性能,提高动态段的跟踪精度,适用轨迹跟踪的运动场景;②优化运动静态段的运动性能,提高静态段的整定效果,适用于点到点的高速高精度定位运动场景;③综合优化动态段和静态段的运动性能,适用于对动态段跟踪精度和静态段整定效果都有一定要求的运动场景。 优化动态段运动性能的适应度函数: (13) 优化静态段运动性能的适应度函数: (14) 综合优化动态段和静态段适应度函数: (15) 式中,n1为动态段计算的结束时间点;n2为静态段计算的结束时间点。适应度函数f1和f2的设计直接使用相应段的位置误差绝对值的累计值作为个体适应度值,适应度函数f3的设计结合了动态段和静态段的位置误差;KDF为动态段适应度计算因子;KSF为静态段适应度计算因子,(k-n1+1)计算因子确保电机运动的位置曲线在静态段的位置误差越来越小,3个计算因子保证了f3适应度函数能够综合优化动态段和静态段,而不会陷入只优化动态段运动性能或者优化静态段运动性能单一优化效果。 由适应度函数的设计可知,适应度值越大,其个体的适应能力越差,越容易在竞争中被淘汰,采用不同适应度函数得到的适应度值不可以进行横向比较。 如图5所示,实验平台使用了广东工业大学精密电子制造技术与装备国家重点实验室中的高速高精度XY运动平台。利用Visual Studio 2010软件的MFC库编写上位机软件和使用DSP开发软件CCES2.8.0编写文中所述的伺服算法和规划算法。本文的运动曲线数据单位采用控制系统单位,即时间单位为250 μs,位置单位为0.4 μm。 图5 XY运动平台 实验中用到了XY运动平台的X轴,采用控制变量法,PID参数保持不变,位置环控制器中,Kp=8,Ki=1.5,Kd=12;速度环控制器中,Kp=20,Ki=0,Kd=0;规划参数保持不变,Sinput=10 000 count,Vinput=250 count/sample_time,Ainput=3.125 count/sample_time2,各阶规划曲线如图6所示。前馈参数为ffKv=0,ffKa=0,ffKj=0,即纯PID控制器输出的控制效果如图7所示。X轴给定的运动过程是从零点位置运动到规划位置,延时150 sample_time,然后运动到零点位置,方便下一次运动。在当前的PID参数和规划参数下,通过改变前馈参数,研究前馈参数对运动性能的影响。 图6 单程的规划各界规划曲线 图7 纯PID控制器的运动效果 图8~图10是控制单一前馈参数,在实验平台上获得的运动位置曲线。图中,CMD_P为位置规划曲线,其余为位置反馈曲线。很容易获取到三个前馈参数约束范围,前馈参数ffKv的约束范围为[-4,3],ffKa的约束范围为[-10,30],ffKj的约束范围为[-50,100]。 图1 “反馈+前馈”控制结构图 图8ffKv前馈参数对 运动的影响效果 图9ffKa前馈参数对 运动的影响效果 由图8~图10可以看出,前馈参数的改变不仅对运动位置曲线的动态段有显著影响,其计算余量对静态段前100 sample_time左右内运动位置曲线也有显著影响。可以确定适应度函数f3的n1=136,n2=236。在运动平台上实验调整,适应度函数f3的KDF=1,KSF=0.2,变异因子F=0.5,交叉因子CR=0.2。如图11所示,通过多次迭代来确定迭代次数和种群规模,在迭代次数G=20,种群规模M=30时,运动平台可以在迭代次数较少的情况下获取良好的运动效果。 图10ffKj前馈参数对 运动的影响效果 图11 使用f2的适应度函数迭代 100代后得到的适应度值 在前馈整定算法参数初值确定后,分别采用3种不同的适应度函数在运动平台上进行实验,获得了3种前馈参数,结果如表1所示。图12~图14可以看出,3种不同设计的适应度函数值随着算法迭代,种群中最佳个体适应度函数值迅速下降,在20次迭代后基本稳定,说明3种个体适应度函数设计有效,前馈整定算法能够在20次迭代能够整定好3个前馈参数。 图12 使用适应度函数f1的适应度值迭代变化图 图13 使用适应度函数f2的适应度值迭代变化图 图14 使用适应度函数f3的适应度值迭代变化图 表1 采用不同适应度函数获取的前馈参数 图15是纯PID控制与使用3种前馈参数复合控制的效果对比图,表2是运动平台采用不同前馈参数的运动性能对比结果,从图15和表2可以看出,纯PID控制的最大动态误差和最大静态误差分别为910 count和641 count,以位置规划±2%的标准得到的整定时间为19 sample_time。使用前馈参数1复合控制的最大动态误差相比于纯PID控制降低了90%,使用前馈参数2复合控制的最大静态误差相比于纯PID控制降低了96.4%,使用前馈参数3复合控制的最大动态误差相比于纯PID控制策略降低了84.1%,最大静态误差相比于纯PID控制降低了90.8%。3种前馈参数的整定时间都为0。实验结果表明,前馈整定算法中个体适应度函数的设计可以获得期望优化效果的前馈参数值,针对动态段运动性能优化获得的前馈参数值适用于提高跟踪精度的运动场景,针对静态段运动性能优化获得的前馈参数值适用于快速定位的运动场景,综合优化获得的前馈参数值适用于对动态段跟踪精度和静态段整定效果都有一定要求的运动场景。 图15 纯PID控制与使用3种前馈参数复合控制的效果对比图(CMD_P为位置规划曲线,ENC_P为位置反馈曲线,PE为位置误差曲线) 表2 纯PID控制与使用3种前馈参数复合控制的运动性能对比 本文基于前馈理论分析,为实现永磁同步直线电机的高速高精度控制,提出采用三环PID+三参数前馈的复合控制策略作为伺服系统的伺服算法,使用四阶S曲线规划算法作为伺服系统的规划算法,在高性能运动控制卡上构建高速高精度伺服系统。针对伺服系统前馈参数整定困难问题,提出使用差分进化算法对3个前馈参数进行智能细调并设计了3种个体适应度函数。从实验结果可以获得以下结论: (1)前馈智能整定算法可以在20次迭代内快速完成整定,获得系统最优前馈值,具有实际的工程应用价值。 (2)前馈智能整定算法的3种个体适应度函数设计对系统的优化效果有导向作用,可以针对性的优化系统动态性能或静态性能,以满足系统在不同运动场景下的性能需求。其中针对静态段性能优化的设计,探索出了利用前馈参数智能整定提高系统定位精度和缩短定位时间的新用法,适合用于高速高精度的点位运动中。2 前馈参数差分进化整定算法
2.1 算法流程设计

2.2 个体适应度函数设计



3 实验验证
3.1 实验平台介绍



3.2 前馈整定算法的参数初值确定

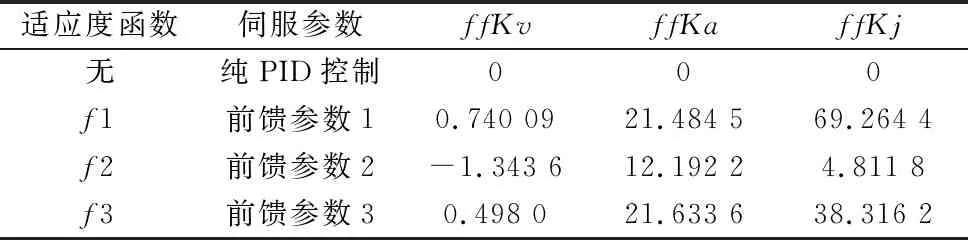
3.3 实验结果与分析


4 结论
