基于改进型粒子群算法的机械臂轨迹规划*

王炳祺，石 敏，朱登明，李兆歆

(1.中国科学院计算技术研究所，北京 100190；2.华北电力大学控制与计算机工程学院，北京 102206)

0 引言

作为工业机器人控制领域中的重要组成部分，轨迹规划不但影响末端轨迹精度，也决定了各关节的运动姿态。若工业机器人在运动过程中速度、加速度发生突变，不能维持运动状态稳定，则会导致末端精度下降，并造成关节磨损和能耗上升。而轨迹规划的目的正是确定一条最优的轨迹，以避免上述情况的发生。在确保机械臂运行稳定后，针对运行时间进行优化以缩短运行时间，对于提升机械臂工作效率具有重要意义。

根据轨迹所在的空间不同，轨迹规划主要划分为笛卡尔空间轨迹规划和关节空间轨迹规划：前者主要针对的是末端执行器，直接规划末端位姿与时间的函数，对末端位置的控制比较方便；后者是直接对机械臂各关节的角度变化进行处理，通过求解关节角与时间的函数，达到控制机械臂的目的。该方法计算量较小，且不会发生奇异性问题，在作业环境不复杂尤其是点到点运动的场景中十分适用。

本文基于关节空间，使用“3-5-3”多项式插值进行轨迹规划，并基于改进型粒子群算法，对轨迹进行时间优化，最终在满足各关节约束和机械臂运行稳定的前提下，缩短了机械臂运行的时间，提升了工作效率。

1 相关工作

轨迹规划作为工业机械臂应用领域的重要问题，许多学者开展了相关研究。KAHN等[1]展开了对样条函数的研究，基于三次多项式的曲线函数进行关节轨迹求解，并开始研究机械臂在点对点运动中轨迹最优的问题；ANGELES等[2]将多项式样条函数分割成分段函数，在关节空间中，将一条完整的运动轨迹分割成多段轨迹，但该方法只适用于具有良好的逆运动学求解算法的前提下，且分段函数的系数计算也较为复杂；BAZAZ等[3]将三次样条插值应用于轨迹规划，最终使速度和加速度曲线保持光滑连续，且计算量较小。

在维持机械臂运动状态稳定的基础上，对轨迹进行优化以缩短运行时间、降低能量损耗、提升运行效率成为了重要问题。田西勇等[4]运用对称组合正弦函数，使关节的最大角速度、角加速度下降，从而减小运动冲击，但同时也降低了运动效率；FRANCISCO等[5]分析了与机器人运动的相关参数，并根据不同影响在机器人实际作业时选择相关的参数进行调整；MULIK等[6]将NSGA-Ⅱ算法应用于B样条插值，并对机械臂进行能耗、加速度等多目标优化的轨迹规划，实验表明该方法能在保持机械臂运行稳定的同时，有效降低能量损耗；ABUDAKKA等[7]利用并行多种群遗传算法，对三次多项式插值轨迹进行时间优化，得到的优化效果较好；ZHANG等[8]利用改进的自适应遗传算法(IAGA)，在功率、速度和加速度的约束下优化了能量损耗；郑涛等[9]针对工业机器人在运动过程中关节速度突变导致的冲击问题，将B样条与5次多项式相结合，提出了“B-5-B算法”，经验证该算法有效地避免了冲击问题；郝晗等[10]对遗传算法进行优化，通过修改初始种群生成方式、改进交叉算子和变异算子的构造过程、设置罚函数解决运动学约束问题等方法，最终完成了对轨迹的时间优化，通过对比实验证明了改进遗传算法相较于普通算法更为有效；SONG等[11]设计了一种基于RBF神经网络的轨迹规划方法，用以解决高自由度机械手的非线性和不确定性问题，保证了机械手在轨迹规划过程中的平稳运行；ZHANG等[12]使用5次B样条曲线算法来平滑运动轨迹，并提出一种高效率、稳定性好的自适应布谷鸟搜索(ACS)算法，以最小化在严格的动态约束下的总运动时间。

综合来看，轨迹规划仍然是目前机械臂控制领域的一项重要问题，在工程应用中，对于提升机械臂运行效率，以及降低机械臂磨损等方面具有实际意义。

2 机械臂模型的建立

为了能够在一个统一的坐标系中准确地描述机械臂以及其他物体的空间位置，一般将机械臂底座作为坐标系原点。而机械臂作为一个由连杆和关节组成的器械，在空间坐标系中需要有特殊的建模方法。D-H建模法是一种用于机器人运动学上的建模方法[13]，本文使用改进D-H建模方法对机械臂进行建模，如图1所示。

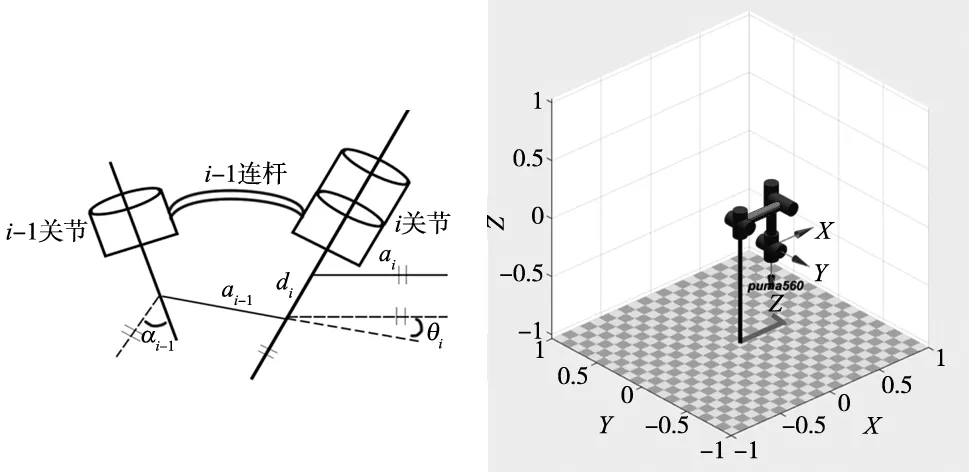
图1 D-H参数表示图2 机械臂仿真模型

图中展示了一段模拟机械臂关节与连杆的图例，各个参数定义如下：

(1)连杆长度ai-1：指两个关节所在轴线间的距离，即公共法线长度。

(2)连杆转角αi-1：指两关节所在轴线间的角度。

(3)连杆距离di：指关节i所在轴线与前后两关节轴线各存在的共两条公共法线间的距离。

(4)两连杆夹角θi：指关节i所在轴线与前后两关节轴线各存在的共两条公共法线间的夹角。

根据上述参数的物理意义，该机械臂的D-H参数如表1所示，括号内为初始角度。

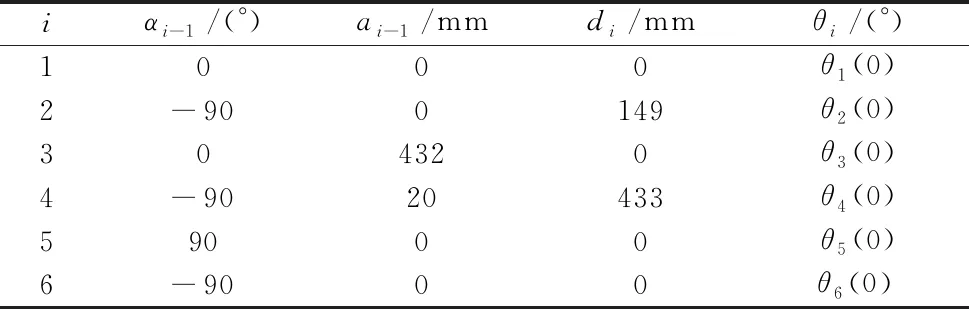
表1 D-H参数

3 优化问题描述

3.1 目标函数定义

在串联机械臂的实际应用中，需要尽可能提升机械臂运行速率，故会导致运行过程中关节的角速度与角加速度的突然增加，导致抖动问题的出现。因此，轨迹规划需要在满足关节约束的条件下按照给定的轨迹点，以时间最短为原则对机械臂运行轨迹进行优化，提升机械臂运行效率。由此可定义优化目标函数为：

(1)

以机械臂在运动过程中各关节的角速度和角加速度作为约束条件，其具体约束为：

(2)

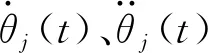
3.2 3-5-3多项式插值

为了保持机械臂关节运行稳定且满足约束条件，需要对关节运动的角速度与角加速度进行控制和规划。在关节空间中常用的规划方法一般是三次或五次多项式插值，但前者无法保证加速度的平滑变化,后者的运算量偏大，而3-5-3多项式插值较好的融合了两者的优点，在多轨迹点规划中有着一定的优势。其具体过程是：在第一段轨迹中使用三次多项式插值，在中间段轨迹中使用五次多项式插值，而最后一段轨迹使用三次多项式插值。实验证明，使用“3-5-3”插值函数进行轨迹规划，具有减小机构冲击，计算量小等优点。

假设共有3段工作轨迹，对机械臂关节j运动参数与时间的函数共有以下3种情况：

当0≤t≤t1时

(3)

当t1≤t≤t1+t2时

(4)

当t1+t2≤t≤t1+t2+t3时

(5)

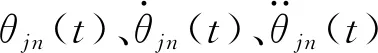
若已知关节在0,t1,t2,t3时刻对应的关节角，并令关节始末角速度和角加速度均为0，且整个过程中角速度与角加速度连续，则可利用矩阵方程对未知系数进行计算，推导过程如下：

m=inv(A)*n

m=[m13m13m11m10m23m24m23m22m21m20m33m32m31m30]T

n=[0 0 0 0 0 0θ3(t1+t2+t3) 0 0θ1(0) 0 0θ3(0)θ2(0)]T

通过上述矩阵方程，即可解出所有多项式系数，获得整段关节运动轨迹，以及角速度与角加速度的变化函数，进而确定在运行过程中是否出现超出关节约束的情况。

4 改进型粒子群算法优化

4.1 基本粒子群算法

粒子群优化算法(PSO)是受到鸟群活动规律的启发，而提出的一种优化算法，利用群体的信息共享驱动群体在问题空间内不断搜索最优解。首先随机生成n组粒子构成初始种群H={X1,X2,…,Xn}，各个粒子位置Xi表示其对应的一个解向量，每个粒子均具有一个速度向量Vi用于决定其运动的方向和距离。迭代过程中，每个粒子根据两个极值来更新自己的变化速度：即粒子本身最优位置和种群最优位置。基于粒子速度来更新粒子的位置用以寻找更优解，粒子的位置和速度随着算法迭代按照如下的式子进行更新：

Vi(k+1)=ωVi(k)+c1r1[pi-Xi(k)]+c2r2[pg-Xi(k)]

(6)

Xi(k+1)=Xi(k)+Vi(k+1)

(7)

式中，ω为惯性权重，用于描述粒子前代速度对当代速度的影响程度；c1、c2为学习因子，描述了粒子对个体最优和种群最优的学习程度；r1、r2为[0,1]区间的随机数；Xi(k)、Vi(k)为第i个粒子在第k次迭代时的位置与速度；pi为粒子的最优位置；pg为种群最优位置。

4.2 改进型粒子群算法

由于传统粒子群算法容易陷入局部最优解，导致种群早熟等问题，参考遗传算法中的变异操作，提出带变异因子的粒子群算法。对于每次迭代的个体，进行随机变异操作，变异过程模拟遗传学中染色体发生基因突变的情况，改变了个体的基因型。发生变异的几率极小，一般为5%以下。变异能够创造原本不存在个体，对种群多样性有积极作用。对个体i进行变异操作，其过程为：

(8)

此外，基于学习率对种群的影响，本文引入收缩因子对粒子群的进化进行约束，以尽可能加速其收敛速度，避免其陷入局部最优。该算法的速度更新方程为：

Vi(k+1)=φ(Vi(k)+c1r1[pi-Xi(k)]+c2r2[pg-Xi(k)])

(9)

Xi(k+1)=Xi(k)+Vi(k+1)

(10)

式中，φ为收缩因子，其计算方法为：

(11)

4.3 基于改进型粒子群算法的时间优化

针对轨迹规划问题，以“3-5-3”插值所用的时间t1,t2,t3为优化目标，利用改进型粒子群算法进行优化。算法使用适应度函数评价解的优劣程度，本文使用的适应度函数如下：

(12)

式中，T为该个体中三段时间t1,t2,t3的总和；Tmax为三段运行时间的最大值，即优化前的默认值；k′为比例系数。使用该适应度函数可以将总时间较短的个体赋予较大的适应度值，而对于不满足约束的个体赋予较低的适应度值。

本文所用的改进型粒子群算法进行时间优化的具体步骤包括：

步骤1：初始化粒子群H，其中每一个粒子位置代表一个解向量Xi=[t1,t2,t3](t1,t2,t3为三段轨迹运行时间)，初始化速度向量Vi=[v1,v2,v3]；

步骤2：根据约束和适应度表达式，计算每个粒子的适应度；

步骤3：寻找并记录粒子个体最优解和种群全局最优解用于速度更新；

步骤4：通过式(9)和式(10)计算各个粒子下一阶段的位置及速度；

步骤5：对粒子进行变异操作并重新计算适应度，基于适应度决定是否保留新的粒子位置，若适应度变高，则保留新的粒子位置，否则不保留；

步骤6：判断是否达到最大迭代次数，若满足判断条件，则寻优结束；若不满足条件，返回步骤2。

5 仿真实验结果

实验使用MATLAB进行仿真，以PUMA560机械臂作为仿真研究对象，通过上述改进型粒子群算法的步骤以及“3-5-3”插值原理，对机械臂关节轨迹进行时间优化，各关节约束条件[14]如表2所示，各关节经过轨迹点如表3所示。

表2 各关节约束条件

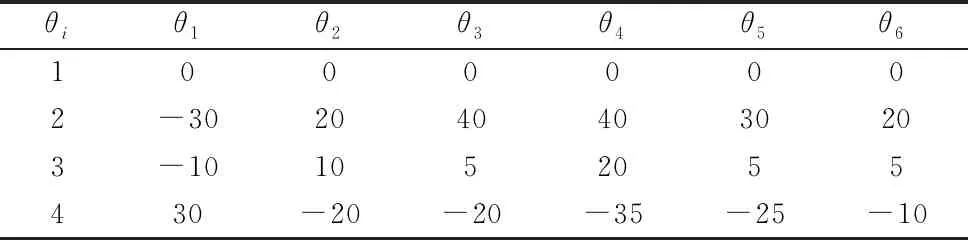
表3 各关节经过的节点 (°)

设置种群大小为100，初始化ti(i=1,2,3)范围[0,4]，Tmax=12，最大迭代次数为200，惯性权重ω=0.9，在传统PSO中c1=c2=1.5，改进型PSO中c1=c2=2.05，变异概率0.05，适应度函数比例系数k′=105。针对同一种群分别使用传统PSO和改进型PSO进行优化，其优化结果如图3和图4所示。

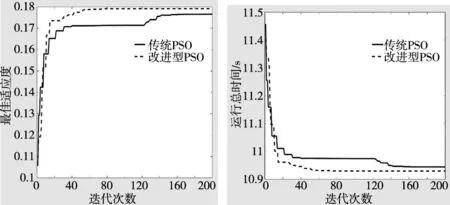
图3 最优适应度变化 图4 最优运行总时间变化

由实验结果可以看出，改进型PSO算法获得的最终运行总时间更短，优化效果更好，并且收敛速度较传统PSO算法更快。将最优解对应的各个关节角、角速度以及角加速度的变化绘制如图5所示。

图5 各关节运动变化曲线

由以上实验结果可以确认，机械臂运动过程中各关节保持平稳，角速度、角加速度变化平滑无突变，并且在满足机械臂各关节的约束条件下，验证了本文所设计的机械臂时间最优轨迹规划方法的有效性。

为了验证改进型PSO算法的优越性，在控制目标函数不变的情况下，与模拟退火算法(SA)、遗传算法(GA)和传统PSO进行实验对照，利用表3的运动轨迹进行5组实验，实验结果如表4所示。

表4 对照实验结果 (s)

综合以上实验结果，在本优化问题中，相比其他传统优化算法，PSO算法能够比较稳定地获得较短的运行总时间，而改进型PSO算法在传统PSO算法的基础上，能够跳出局部最优，获得更优的解，且收敛速度更快，能够获得更优秀的机械臂运行轨迹。

6 结论

针对串联机械臂时间最优轨迹规划问题，在关节空间内，以“3-5-3”插值轨迹规划算法为基础，基于改进型粒子群算法对该规划方法进行时间优化。实验表明改进型粒子群算法与传统粒子群算法相比，能够跳出局部最优获得更优解，且收敛速度更快。在与其他优化算法对比中，改进型粒子群算法有更强的收敛一致性，且优化效果更好。经过该算法优化过的轨迹，关节角速度、角加速度过度平滑且均满足约束条件，有效缩短了运行时间，提高了机械臂运行效率。

接下来的工作可以围绕效果更好的优化算法进行展开，例如利用神经网络对目标进行优化以获得更好的效果。此外也可以针对笛卡尔空间中机械臂末端轨迹进行优化控制，以应对更为复杂的情况。