一种能量级自然云雷达图像仿真方法

余应福，徐 涛，方 君

（海军航空大学，山东烟台 264001）

模拟训练作为当前重要的训练手段之一，其对仿真系统的逼真性和实时性的要求越来越高。机载雷达系统作为飞行器的重要航空电子设备，主要用于导航、目标探测与武器目标指示。飞行模拟训练中，雷达仿真是装备仿真中的重要组成部分，仿真能力包括可判读信息生成（如雷达图像）和目标航迹生成等，其仿真效果直接影响训练系统的性能发挥。而对自然云的雷达仿真，不论是将云作为探测目标还是考虑云对雷达目标（舰艇、地形等）探测的影响，其雷达回波图像仿真都会直接影响雷达设备仿真的真实性和训练设备的功能性。

目前，国外的自然云雷达图像和信号衰减仿真技术已经广泛应用于军事仿真和民用飞行仿真，如：美国Camber 公司开发了包含自然云的雷达成像仿真开发包[1]，可支持用户二次开发；Milviz 公司的WX Advantage Weather Radar System[2]虽可集成到FSX、P3D等飞行仿真引擎，却难以应用于自主研发的模拟系统中。我国也针对不同的应用需求开发出了多种仿真系统：基于物理过程的雷达图像仿真，可以获得更好的成像效果，但需要根据降水物质粒子谱分布来计算雷达波束内不同直径粒子的回波能量并进行叠加，不但计算量大，而且需要建立复杂的物理模型并进行推演，仿真复杂度高[3-4]，难以满足模拟训练系统的实时性要求[5-7]；用于机载气象雷达仿真的方法，虽然可以很好地模拟气象雷达成像效果，但却忽略了雷达波束充塞系数对云的雷达图像仿真的影响，或者没有体现雷达回波能量计算和信号在云中的衰减[8-9]。

本文基于机载雷达探测云雨区域的物理过程，利用云雨目标雷达散射的统计特性，对自然云雷达信号衰减和回波能量进行建模，并对雷达成像仿真方法进行优化设计，从而缩短仿真的用时，降低仿真空间的复杂度。可将该模型作为1个低复杂度的自然云雷达仿真模块，因其对设备硬件性能的要求低，故有助于提升机载雷达仿真系统的仿真度。

1 自然云雷达图像仿真方法

1.1 云模型定义

云的结构形状多变，云中所含有的降水物质的形态、大小不能被精准测量，通常只能根据气象探测数据进行估计，并分析云中水粒子的形态、大小等参数。在科学实验中，对云和降水的雷达特性进行仿真，需要精确的物理模型[5-6]以及水粒子的雷达散射模型，计算雷达回波和衰减，系统复杂度高、模型设计困难[10]，模拟训练仿真中建立这种复杂的模型，对使用者的专业能力要求过高且实验不易操作。在对雷达探测数据的分析和观测中，学者得出了云的降雨量或者云中含水量和雷达反射率之间的关系[11-13]，用雷达反射率体现不同频率电磁波对云、雨的探测情况，将这个参数作为电磁特性数据，应用于雷达仿真中，可使云中粒子的微观电磁特性更加直观。观察气象雷达的回波图像可发现，虽然云的外形变化多样，但是雷达回波强度带有区域分层的特性[14]。

气象雷达图像体现为不同强度回波的嵌套，考虑云团的高度和厚度，本文采用嵌套的多面体构建云团，每个多面体由多边形生成并关联其所包围区域内的降雨率，多边形内部的降雨率会被嵌套的多边形的降雨率替换。图1 为简单云团模型的俯视图，顶面不同颜色区域表示不同的降雨率。

图1 简单云团结构示意图Fig.1 Structure of a simple cloud cluster

为了便于云场景设计，简单云团模型顶点坐标采用极坐标的形式保存，坐标中心在云团的几何中心。对顶点坐标进行归一化，可以根据仿真需要调整简单云团的中心位置、高度、水平范围以改变云团，也可以调整云团移动速度、降雨率衰减系数，以实现云团在场景中的移动和消散。将多个简单云团组合构建成复杂的云团以提高模型的精细度，比如雷暴云通常由不同高度的3 部分云体组成：底部云体是反射率最高的部分，中部云体有中度的反射率，顶部极少反射。通过构建多个简单云团，可以模拟雷暴云不同云体的雷达回波特性。

1.2 仿真流程

仿真中，模拟雷达对云团的探测和回波能量计算，需要确定雷达和云团的位置关系，根据雷达波束参数和云团分布，判断波束照射区域内的云团，并获取雷达各个距离分辨单元内的降雨率。将降雨率转化为云雨粒子在单位体积内的雷达反射率和单位距离上的衰减系数，进而计算雷达各距离分辨单元的回波能量和传输路径上的电磁波衰减系数，最终生成雷达图像。仿真过程，如图2所示。

图2 仿真流程图Fig.2 Simulation flowchart

坐标转换中，雷达和云团中心位置使用的是地理坐标系，需要根据云团的本地坐标系将云团顶点转换到以雷达位置为原点的雷达坐标系。本文的云模型为垂直地面的多面柱体，将雷达坐标系下的云团顶点坐标转换到地面投影坐标系，将三维空间的解算过程转换到二维平面进行，从而降低判断波束是否照射到云团的计算复杂度。

2 关键模型实现

2.1 波束充塞系数近似策略

气象雷达方程中的波束充塞系数对雷达图像的效果有很大影响[15-16]，雷达波束照射范围是1个立体空间，在设定单位体积内云雨粒子的雷达反射率后，计算雷达回波能量需要确定有效照射体的体积，以获取目标区域的雷达反射截面积。如图3所示的雷达波束的2 个照射体V1 和V2，网格填充区域为对应的有效照射体，∆d为雷达距离分辨率。由于雷达波束在近距离时的线宽度小，远距离时的线宽度大，使得照射体V1 完全处于云区内，雷达有效照射的体积即照射体V1 的体积，其充塞系数为1。照射体V2 没有充满降水粒子，有效照射的体积减小，其充塞系数应小于1。根据雷达天线参数可以计算照射体V1和V2的体积，由于云形状的不确定性及波束与云的位置关系的复杂性，仿真中难以计算波束充塞系数以获得照射体中的雷达反射截面积，因此，文中采用估算模型，将雷达波束主瓣宽度按照垂直方向和水平方向进行采样，等角度间隔划分为多个子波束。

图3 波束充塞情况示意图Fig.3 Illustration of beam filling

假设雷达波束相对正北（z轴）的方位角度（文中角度变量单位统一使用弧度）从a1到a2，将水平波束宽度分为M等份，采样间隔为∆θ，则第i个采样角度θi=α1+i∆θ-∆θ/2 ，i=1,2,...,M。在天线方位角θi下，经过雷达位置作垂直于地面的截面，雷达波束垂直截面相对水平面的俯仰角度（向上为正）从β1到β2，将垂直波束角度分为N等份，采样间隔∆φ，则第j个采样角度φj=β1+j∆φ-∆φ/2，j=1,2,...,N。

对于任意1条从雷达位置开始，方位角θi，俯仰角φj的射线ρij，求解ρij与场景中云团相交情况，确定该射线穿越云区时的不同距离上的降雨率。每个子单元依据该单元中心线是否穿过云体来判断其与云团是否相交，将相同距离分辨率内的各个子单元中的能量相加作为该距离分辨单元的能量，实现对波束充塞系数的近似计算。

2.2 回波功率计算

考虑云雨对电磁波的衰减和天线的方向性，单个云雨粒子的气象雷达方程为[13]：

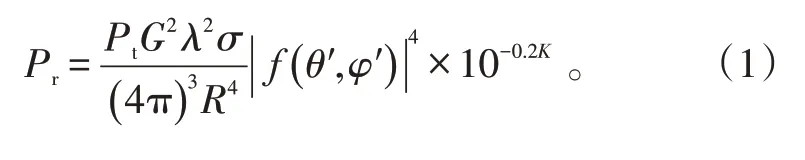
式（1）中：Pr是雷达接收到的信号功率；Pt是雷达发射的峰值功率；G是天线增益；λ是雷达电磁波波长；σ是目标的散射截面积；R是雷达与目标物之间的距离；雷达天线的归一化方向图函数为f( )θ′,φ′ ，其中θ′、φ′为目标方向偏离雷达波束最大辐射方向的水平和垂直角度；K为电磁波传输路径上云雨粒子的衰减系数。

通过对雷达波束进行水平和垂直方向的二维采样，在方位角θi下第j个波束垂直采样角中第l个距离单元的距离为Rl，这个照射体中的雷达回波是所有云雨粒子反射能量的总和。假设单元内雷达天线增益和粒子的尺度谱均相同，其回波能量为：

式（4）中：m是散射粒子的复折射率；Z是雷达反射率因子。Z可以表示为降雨率I的函数，即Z=AIb。参数A、b是经验性的常数，常用的典型关系式是Z=200I1.6。

根据能量方程，Pijl的计算需要获取降雨率I以及衰减系数K。

2.3 自然云参数获取

根据文中云模型的特点及空间关系，将三维空间的计算转化到二维平面上，以降低计算复杂性。通过求交点计算，确定子波束方向上不同距离的降雨率。

将射线ρij投影到地面坐标系的xoz平面，形成射线ρi，其起点在雷达地面位置，和z轴的夹角为θi；同样，将构成云团的多面体投影到xoz平面，形成投影多边形，计算射线ρi与各多边形的交点，根据求取的交点计算ρij与多面体侧面和上下底面的交点。

假设地面投影坐标系下的交点坐标为PIvn(xvn,zvn)，其中vn=1,2,…,vm，雷达高度hr，云团中心高度hc，云团厚度hv，通过云团的厚度及中心高度计算云底和云顶高度，结合雷达高度、射线ρij的俯仰角φj，计算射线ρij与过交点PIvn且垂直xoz面的直线的交点坐标Bvn(xvn,zvn,yvn)，则：

该坐标点即射线ρij与云团的多面体在雷达坐标系下的交点，对任意的交点坐标Bvn，计算其至原点的距离Dvn，将所述交点至原点的距离按照大小排序。

当φj≠0 时，射线ρij到多面体的最大、最小距离为：

通过处理交点序列以及气象模拟场景中加载的交点所在多面体的降雨率，可获得各个距离段的模型参数。

2.4 衰减系数的计算

在回波计算时，将1个波位下的波束照射空间（天线波束主瓣所包含的空间）按方位和俯仰角度划分为M×N个子单元。对第(i,j)个子单元，其中心产生的射线ρij和云的各多面体的交点按由近到远顺序存入线性链表中，图4 为射线起点到雷达最大作用距离之间的交点及交点间的降雨率I。

图4 传输路径上的降雨率Fig.4 Rainfall rate along the direction of beam

图中线段起点为雷达位置，终点为雷达最大作用距离，之间的8个点为射线与多面体的交点，相同灰度的线段表示相等的降雨率，I0为大气中的降雨率，各个交点到射线端点的距离为dm。对每1 条线段以雷达距离分辨率∆d采样，第m和m+1 个交点间的距离分辨单元个数为：

常数因子c、e由雷达信号频率决定，可以通过ITU-R P.838-3建议书给出的参数和公式计算[18]。

3 实验分析

3.1 实验条件设置

1）雷达参数：工作频率10 GHz，天线水平波束宽度1.5°，仰角4°，扫描范围60°，载机位置（121.448°E，37.363°N，3 000 m）。

2）云模型：设置了2个云团进行测试，云团1的中心位置（121.414°E，37.542°N，4 000 m），厚度4 km，最大范围16 km；云团2中心位置（121.357°E，37.633°N，3 000 m），厚度3 km，最大范围24 km。云模型地面坐标系投影，如图5所示。

图5 云模型地面坐标系投影图Fig.5 Projection of cloud model in ground coordinate system

3）软件实现环境：基于windows 10 操作系统，CPU 为Intel Core i7-7700 @ 3.6 GHz，内 存 为Dual DDR4 SDRAM 16.0 GB，采用Visual C++2010开发环境实现仿真算法并进行测试。

3.2 回波图像分析

为测试云的衰减效应，以及波束充塞度对回波图像仿真的影响，共生成3幅回波图像，如图6所示。其中：图6 a）是采用本文算法生成的回波图像，波束采样为5×3；图6 b）中波束采样为5×3，回波仿真时没有考虑电磁波传输过程中云所造成的衰减；图6 c）对应的回波计算过程忽略了波束充塞系数的计算，即波束采样为1×1。

图6 云回波图像Fig.6 Simulated echo images

对比图6 b）与图6 a），由于没有考虑云的衰减，图6 b）亮度（对应回波强度）整体偏高，且与雷达距离越远，图像处于相同位置云单元的回波能量相差越大。可见，在雷达图像仿真应用中，如RBGM图像仿真中，如果不考虑云的衰减效应，则会造成仿真图像较为明显的失真。

3.3 实时性分析

波束充塞度的计算通过对波束采样进行近似，采样数的增加会导致算法用时的增加，图7 给出了不同采样次数下的各个波位的回波计算耗时，波位间隔为0.36°。假设天线扫描周期为3 s，为满足实时仿真需求，每个波位的回波计算耗时不应超过18 ms。由图7可见，本文算法可以满足云回波图像实时仿真需求。

图7 不同波束采样下各波位的回波计算耗时Fig.7 Time consumption of echo calculation of different beam sampling methods

4 结束语

本文利用自然云雷达成像的统计特性，结合雷达成像的物理过程，设计了基于降雨率的三维云模型的雷达成像仿真方案，通过算法实现和仿真结果比较，可以实现逼真度较高的雷达回波模拟。文中算法涉及射线和空间中云体的相交计算，随着波束采样和云模型的增加，算法时间复杂度也在增大，下一步可以对算法进行深入优化。同时，也可以扩展算法功能，开展云背景下地物、空中目标的成像仿真。