基于多尺度3D-2D卷积神经网络的高光谱图像分类

吴俊峰，高 龙，王 超，徐从安，闫文君

（海军航空大学，山东烟台 264000）

0 引言

随着成像技术的日趋成熟，高光谱图像不仅可以提供越来越丰富的谱域和空域信息，还能更详细地描述地物特征。由于高光谱图像优势明显，高光谱分类技术已经逐渐成为对地观测的重要手段，在环境保护、农业和地理观测等领域具有广泛应用[1-2]。

早期高光谱图像分类方法主要关注于如何提取有效的光谱特征，以解决多波段、高冗余带来的维度灾难问题。降维和传统分类器相结合的方法成为常见的分类手段，如主成分分析（Principal Component Analysis，PCA）、独立成分分析[3]、K 近邻、支持向量机（Support Vector Machine，SVM）[4]等。但相关方法始终无法有效解决高光谱图像存在严重的“同谱异物，同物异谱”的问题[5-6]。为了进一步提升分类效果，很多学者提出空谱融合的高光谱图像分类方法，如条件随机场[7]、稀疏表示[8]和多核学习[9-10]等。

近年来，卷积神经网络（Convolutional Neural Networks，CNN）[11-12]已经成为解决高光谱图像分类任务的有效方法。Hu等[13]提出1种5层卷积神经网络用于高光谱图像分类，取得了更好的分类效果；Yue等[14]将高光谱图像中的空间信息和光谱信息融合后引入到CNN模型，进一步提升了分类效果；Liang等[15]基于协同稀疏自编码构建了光谱-空间特征融合机制，并利用SVM 实现分类；Zhao 等[16]利用孪生神经网络提取相邻像素对的光谱和空间关系信息，并利用softmax损失函数实现分类；Zhao等[17]基于稠密卷积和条件随机场构造了新的分类方法，该方法利用稠密连接神经网络提取光谱特征，利用条件随机场整合全局空间信息；Wu等[18]利用1D-CNN和2D-CNN分别提取光谱和空间特征，并构建了二分支网络架构来实现高光谱分类。相关研究表明，基于CNN，将光谱信息和空间信息进行融合，能够有效提升高光谱图像分类精度。但是目前，高光谱图像分类相关研究主要以2D-CNN 为主，在进行特征提取时需要对网络中每1 个二维输入进行卷积，每1 个光谱波段都有1 组待学习的核。拥有数百个光谱波段的高光谱图像的分类，通常需要大量的卷积核，这需要消耗大量的计算资源，且容易造成过度拟合[19]。同时，空间信息提取以某一波段的平面空间信息为主，较少考虑不同波段之间的立体空间信息。为此，Chen 等[19]提出了3D-CNN，通过3D 卷积核实现光谱信息和立体空间信息的同时提取和融合，有效提升了分类效果；Wang等[20]将通道注意力机制和空间注意力机制引入3D-CNN 模型中，从而获得了更具判别性的广域-空间特征；Feng 等[21]基于残差思想提出了11层残差3D-2D模型，有效解决了小样本条件下的高光谱分类问题；Roy 等[22]基于3D-CNN 和2DCNN 提出HybridSN 网络，3D-CNN 用于提取光谱-立体空间信息，2D-CNN 则进一步提取平面空间信息。基于3D-CNN 的相关方法提升了空间信息的利用程度，但是这些研究都只考虑了1种尺度的空间特征，未考虑不同地表覆盖的尺度特性。

为提升高光谱分类效果，本文基于HybridSN，提出多尺度3D-MSCNN 网络。首先，采用PCA 对高光谱数据进行降维；然后，利用3D空谱特征提取网络和2D多尺度特征提取网络实现高光谱图像特征提取；最后，利用Softmax 分类损失函数实现高光谱图像分类任务。

1 3D卷积

图1 2D和3D卷积的基本实现过程Fig.1 Process of 2D and 3D convolution

2 3D-MSCNN网络

3D-MSCNN 通过引入多尺度特征提取网络来提升网络性能。网络结构，如图2 所示。其主要分为4个部分——数据处理、空谱特征提取网络、多尺度特征提取网络和输出网络。

图2 3D-MSCNN网络模型结构示意图Fig.2 Network structure of 3D-MSCNN

2.1 数据处理

高光谱图像波段数较多，数据量大，信息冗余度高，容易出现维数灾难现象。为克服上述问题，对于给定高光谱图像I∈ℝW×H×L，利用PCA进行降维，去除无用波段，获得高光谱图像X∈ℝW×H×L，其中：W、H为高光谱图像的宽度和高度；L、D分别表示降维前后图像的光谱波段数。然后，对X进行边缘填充，并以每个像素pij为中心提取尺寸为S×S×D的高光谱数据立方体Bij，1 ≤i≤W，1 ≤j≤H。每个数据立方体的标签由中心像素的标签yij决定。为了降低不同波段光谱量化范围对高光谱图像分类精度的影响，对高光谱图像X按波段进行归一化，如式（3）所示。

2.2 空谱特征提取网络

的数据立方体尺寸为23×23×24；经过第2 个3D 卷积层后的数据立方体尺寸为21×21×20；经过第3个3D卷积层后的数据立方体尺寸为19×19×18。

表1 空谱特征提取网络结构参数Tab.1 Parameters of spatial-spectral feature extraction network

2.3 多尺度特征提取网络

为提升不同尺度地物的特征表达能力，在3D 空谱特征提取网络后接入特征金字塔网络，如表2 所示。在该结构中：首先，对空谱特征提取网络获得的数据立方体Feature3 进行reshape 处理，获得2D 特征图谱M1，对M1 进行自底向上的2 次2D 卷积和maxpooling 下采样，分别获得不同尺度的特征图M2 和M3；然后，利用最近邻内插法对M3 进行自顶向下的上采样，并逐级在M2 和M1 层之间建立1×1 卷积横向连接，逐步得到特征图P2 和P1；最后，利用Flatten层将特征图一维化，并连接2 个参数为1×1×1024 的全连接层，每个全连接层采用Dropout 方法随机丢弃50%的隐藏层节点，以控制过拟合的风险。

表2 多尺度特征提取网络结构参数Tab.2 Parameters of multiscale feature extraction network

2.4 输出网络

在输出网络构建softmax 损失函数，完成高光谱图像的多分类任务。在训练过程中，采用随机梯度下降（Stochastic Gradient Descent，SGD）优化器优化目标函数，对参数进行学习，得到每个像元所属的类别。

3 实验结果与分析

为了验证本文算法的分类能力，本文在2 个公开数据集，即印第安纳州农场（Indian Pines）数据集和帕维亚大学（Pavia University）数据集进行实验。选择总体精度（Overall Accuracy，OA）、平均分类精度（Average Accuracy，AA）和Kappa[22]系数作为定量评价指标，并与SVM[23]、CD-CNN[24]、3D-CNN[25]、SS-Net[12]和HybirdSN[22]等方法进行比较。为保证评价指标的客观性，进行10次独立重复实验来获取相关指标数据。

3.1 实验数据集

1）Indian Pines数据集

Indian Pines 数据集是利用AVIRIS 光谱仪拍摄的印第安纳州一片农场的高光谱图像，其伪彩色图像和真值图，如图3 a）、b）所示。该高光谱图像长宽为145×145，光谱波段数为220，图中包含森林、草甸、玉米、小麦和柏油路等16 类地物。该场景下，训练和测试样本数，如表3所示。

图3 Indian Pines和Pavia University高光谱图像Fig.3 Hyperspectral images of Indian Pines and Pavia University

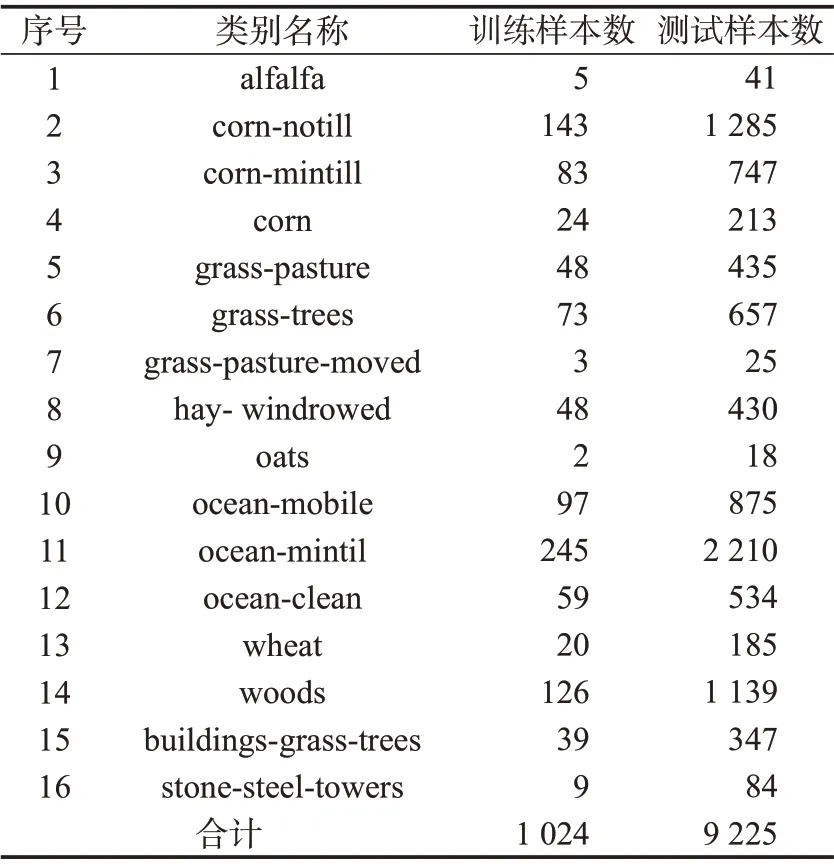
表3 Indian Pines数据集的训练和测试样本统计Tab.3 Training and testing set of Indian Pines

2）Pavia University数据集

Pavia University数据集是利用ROSIS光谱仪拍摄的意大利北部帕维亚大学的高光谱图像，其伪彩色图像和真值图，如图3 c）、d）所示。该高光谱图像长宽为610×340，光谱波段数为103，包含林地、建筑物和马路等9类地物。该场景下，训练和测试样本数，如表4所示。

表4 Pavia University数据集的训练和测试样本统计Tab.4 Training and testing set of Pavia University

3.2 参数设置

在Indian Pines 数据集上，通过PCA 降维，波段数D=30，数据立方体参数S=35；在Pavia University 数据集上，D=15，S=31。在2个数据集上，epoch均设置为1 000，学习率为0.001，批大小（batch size）为10。实验硬件条件为Intel Core i7 双核处理器、Nvidia GTX2080 GPU 和32 G 内存。实验软件条件为CUDA10.0、CUDNN7.6.0、Tensorflow1.13.1和Python3.6。

3.3 结果与分析

本文算法在Indian Pines和Pavia University数据集上的分类效果，如图4、5所示。

图4 Indian Pines数据集上不同算法分类效果图Fig.4 Classification results of different algorithms on Indian Pines dataset

图5 Pavia University数据集上不同算法分类效果图Fig.5 Classification results of different algorithms on Pavia University dataset

从图4、5 中可以看出，本文算法获得的分类结果图像具有清晰的边缘轮廓，包含更少的噪声，更加接近真值图。不同算法在Indian Pines和Pavia University数据集的客观评价指标，如表5所示。

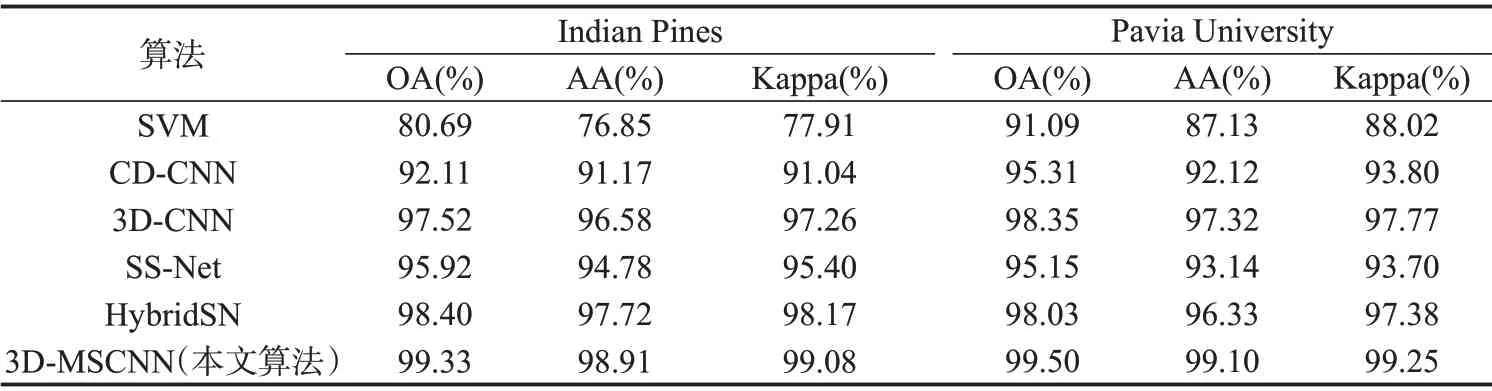
表5 不同算法在Indian Pines和Pavia University数据集上的客观评价指标统计结果Tab.5 Statistics results of different methods for object evaluation indicators on Indian Pines and Pavia University datasets

从表5可以看出，本文算法的OA、AA和Kappa均超过其他方法，表现出了较为明显的性能优势。与HybridSN 相比：本文算法在India Pines 数据集上性能分别提升了0.10%@OA、1.20%@AA 和0.93%@Kappa；在Pavia University 数据集上分别提升了1.50%@OA、2.98%@AA和1.95%@Kappa。结果表明，本文算法通过引入多尺度机制，能进一步提升HybridSN网络性能和分类效果。由于不同的地表覆盖分辨率不同，所以数据立方体Bij的参数S对3D-MSCNN 精度影响较大，如图6所示。

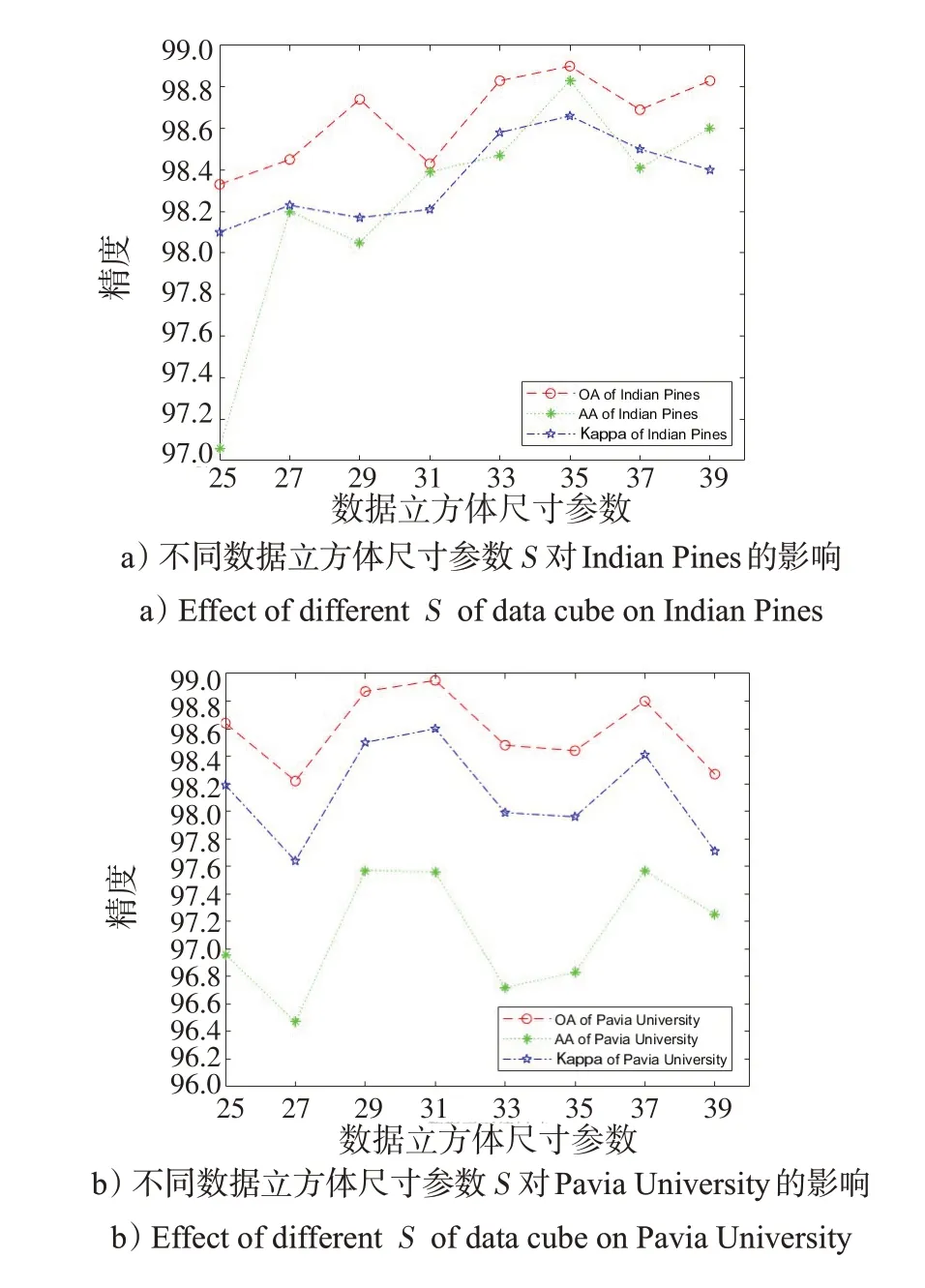
图6 不同数据立方体尺寸参数S 对本文算法的影响Fig.6 Effect of different S of data cube for the proposed 3D-MSCNN

在Indian Pines 中，OA、AA 和Kappa 系数随着S的增加呈现先上升后下降的趋势，并在S=35 时，本文算法表现最好；在Pavia University 中，虽OA、AA 和Kappa 系数的波动性较大，但仍然可以看出，当S=31时本文算法取得了较好的精度。

4 结语

本文设计提出了1 种针对高光谱图像分类的3DMSCNN 模型。首先，采用PCA 对高光谱数据进行降维；然后，利用3D 空谱特征提取网络和2D 多尺度特征提取网络实现高光谱图像特征提取；最后，利用Softmax分类损失函数实现高光谱图像分类任务。本文在构建网络时，在HybridSN网络基础上引入多尺度思想，充分发挥了高光谱图像空谱信息价值，增强了对不同尺度地表覆盖的表达能力，提升了高光谱图像的分类效果。在Indian Pines 和Pavia University 数据集上的实验结果验证了本文算法的有效性。