航空器海上飞行空域规划方法
2022-11-23刘玉杰綦庆庆
刘玉杰,韩 维,綦庆庆,郭 放,刘 洁
(1.海军航空大学,山东烟台, 264001;2.中国民用航空局空中交通管理局航行情报服务中心,北京, 100012;3.军事科学院,北京, 100850)
0 引言
近年来,随着我国经济和军事的高速发展,周边海上空域各类航空器飞行活动日益频繁,军、民航对海上空域的需求均呈现增长态势,对海上空域使用的范围和频次持续加大。面对有限的海上空域资源,如何寻求1 种高效精准的空域规划方法,对缓解我国海上空域资源紧张问题十分重要。
海上空域分布情况复杂,探索1 种高效精准的海上空域可用资源规划方法,通过智能优化算法,空管人员对海上空域调配问题进行决策,对海上可用空域资源进行深度挖潜,以达到对海上可用空域资源进行最优配置的目的,可有效缓解航空器海上飞行空域资源紧张问题。从军事需求看,空域是1 种重要的作战资源,对空域资源进行精细化管理和实时控制[1],有利于科学配置可用空域资源,实现空域用户的联合协同,避免误伤和贻误战机,同时,也有利于及时发现并处理空域冲突,较大限度的降低联合作战中的空域使用限制,从而充分发挥联合作战效能[2];从民用需求看,对空域资源进行精细化管理和实时控制,同样可以有效提高空域使用效率,进而更好地降低航班延误率、提高通用航空海上空域使用审批效率,同时有利于更好地保证飞行安全。
目前,国内针对航空器海上飞行空域资源配置问题的研究,还没有相对成熟的智能规划方法和理论体系。主要还是依靠空管人员的经验,通过人为划设的方法对空域进行规划[3],受组织人员能力影响较大[4],这也带来了空域利用率低、机动灵活性差等方面的问题。
从目前研究看,寻找航空器海上飞行可用空域资源的过程与物联网直接寻址的过程相类似,都是逐级迭代的过程——每1级的输出结果都作为下一级的输入变量,层层迭代,直到得到最终节点的逻辑地址停止。这种迭代关系使得每1 层解析独立于整个过程,并不需要输入所有层次的信息,每个层次的寻址系统只需完成本层次的解析,并把结果输入到下一层次[5]。这种迭代关系降低了层次间的相互耦合作用,解析更加机动灵活[6]。
目前,物联网寻址问题可分为2种:
1)直接寻址,即通过寻址模型直接指出携带该物联网资源节点的逻辑位置,不需要通过某种变换[7];
2)间接寻址,即通过寻址模型定位该物联网资源节点的上级资源的逻辑位置,然后通过迭代运算由该定位位置得到物联网资源的逻辑位置[8]。
根据物联网直接寻址的特性,本文将这种寻址思想应用到寻找航空器海上飞行可用空域资源问题中,得到航空器海上空域资源规划流程,如图1 所示。为提高搜索算法的实时性,减少计算量,在搜索可用空域资源时,目标搜索算法必须尽最大可能尽快捕获到所需目标。因此,本文在穷举法的基础上[9],选用改进的协同区域随机搜索算法,以合理分配资源为目的,设置相应限制条件,尽快发现海上可用空域资源。
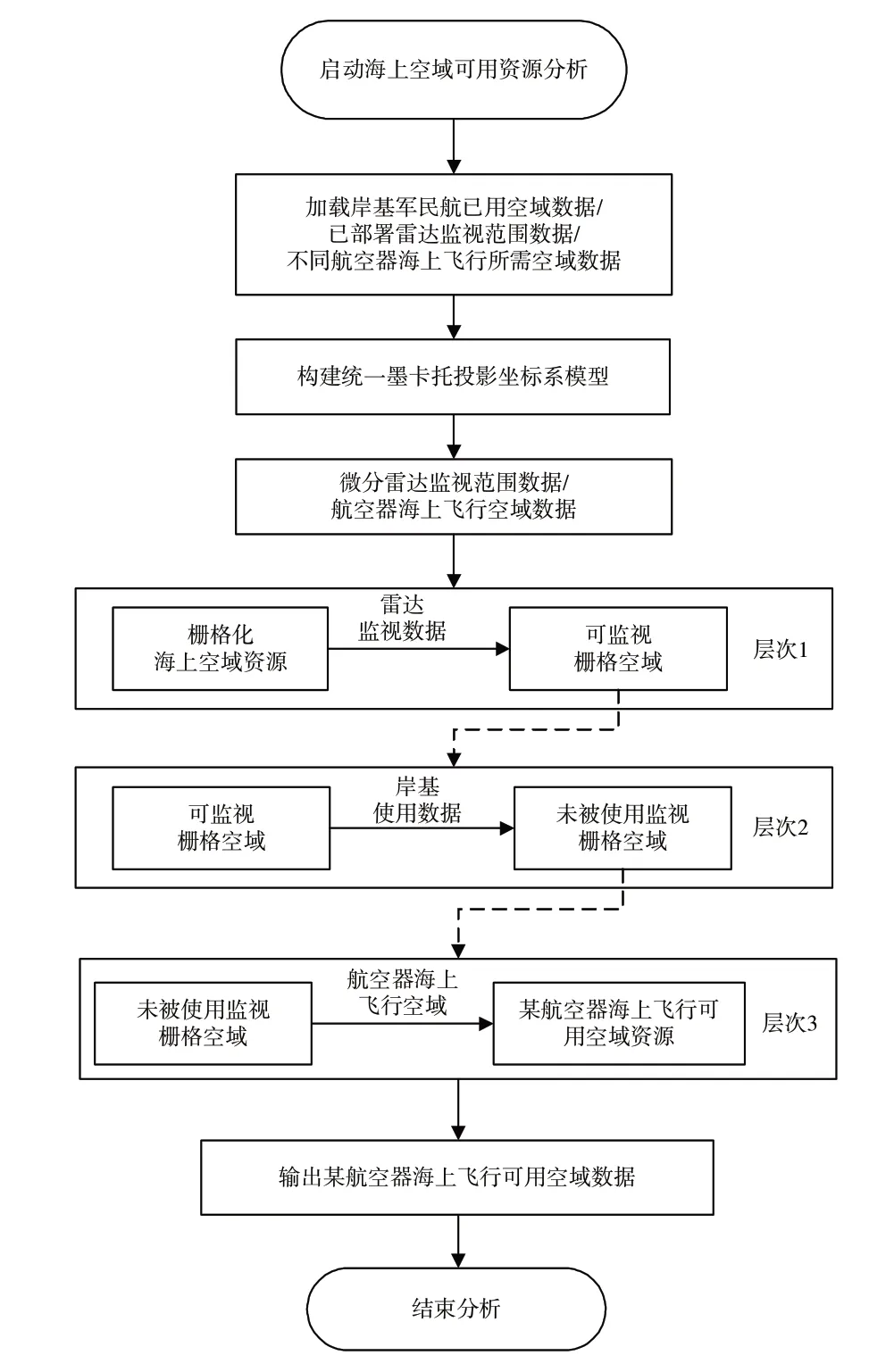
图1 海上空域资源规划流程图Fig.1 Flowchart of maritime airspace resources planning
1 数据基础
1.1 投影坐标系的选择
地图投影是利用一定数学法则把地球表面的经、纬线转换到平面上的理论和方法[10],由于运用任何数学方法进行转换都会产生误差和变形,因此,应按照研究需求进行投影方法的选择。地图投影按变形方式可以分为等角、等积和任意投影3 种[11]。等角投影是指投影面上某点的任意两方向线夹角与地球椭球面上相应线段的夹角相等的投影,即角度变形等于0[12],其长度比在一点上不随方向的改变而改变,但在不同地点,长度比数值是不同的。因此,从大范围来说,图上投影图形与实地并不相似。由于这类投影没有角度变形,故多用于对方向精度要求高的航海图、航空图、洋流图、风向图和军用地图等[13]的绘制。等积投影是地图上任一图形面积与实地上相应的面积相等的投影,即面积变形等于0[14]。为了保持等积条件,需使面积比等于1,使用这类投影的地图便于进行面积比较,多用于经济地图和政区地图[15]。任意投影是既不等角又不等积的投影。在这种投影图上,长度变形、面积变形和角度变形同时存在。在任意投影中有1种比较常见的等距投影,适用于要求面积变形不大,角度变形也不大的地图,多用于一般参考用图和教学用图[16]。
针对航空器飞行的特殊要求,应尽可能保证方向和角度的真实性和准确性,满足实时监控、导航和规划的精度要求以及与实地的一致性。因此,综合考虑各种投影的变形特征,在本系统应用中,采用等角投影中的墨卡托投影坐标系。
1.2 数据处理
加载岸基军、民航已用空域数据,加载已部署的航管雷达监视范围数据,加载不同航空器飞行所需空域范围数据,对数据进行预处理。构建墨卡托投影坐标系模型,将每个雷达监视范围区域和典型海上飞行空域进行投影,将投影面积划分成N等分(N=360)的多边形区域[17],如图2所示。
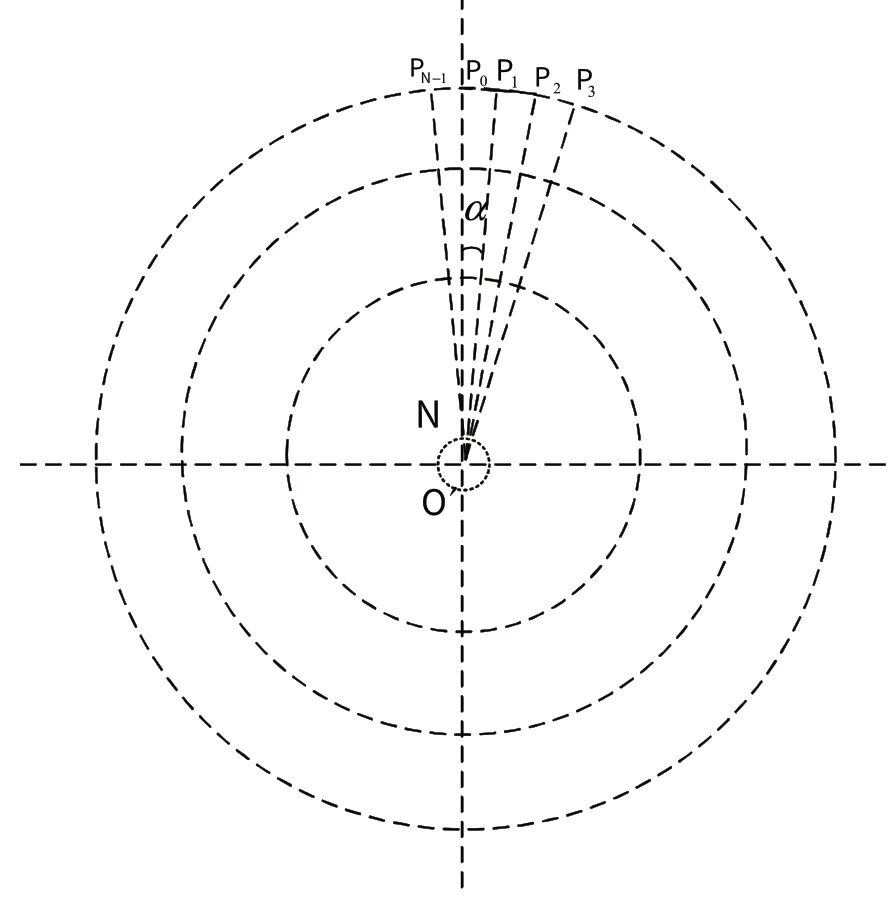
图2 投影区域N等分示意图Fig.2 Schematic diagram of N equal parts of the projection area
2 模型建立
首先,基于墨卡托投影坐标系[18]将海上空域范围投影到直角坐标中,按适应性间距将其划分成正方形栅格区域,其中空域行号划分成为m个,列号为n个,共 计m×n个 栅 格,每 1 个 栅 格 编 号 为fij(i=1,2,…,m;j=1,2,…,n),其中(i,j)表示空域坐标,每个栅格用直角坐标进行唯一表示,如图3所示。

图3 栅格化海上飞行空域资源示意图Fig.3 Schematic diagram of rasterized maritime flight airspace resources
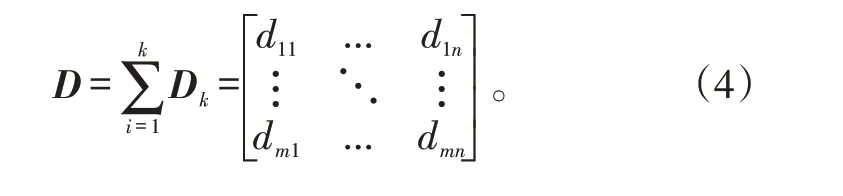
建立栅格区域矩阵F,表示栅格化的海上飞行空域资源:

然后,根据雷达信号范围形状,将地面投影近似圆形处理,建立雷达站点矩阵R,对雷达监视范围进行数学抽象,表示雷达站点位置。

其次,建立雷达站点覆盖矩阵Dk,定义为第k个雷达站点对栅格空域第fij栅格的覆盖情况,判断雷达监视覆盖范围与栅格化空域的位置关系。

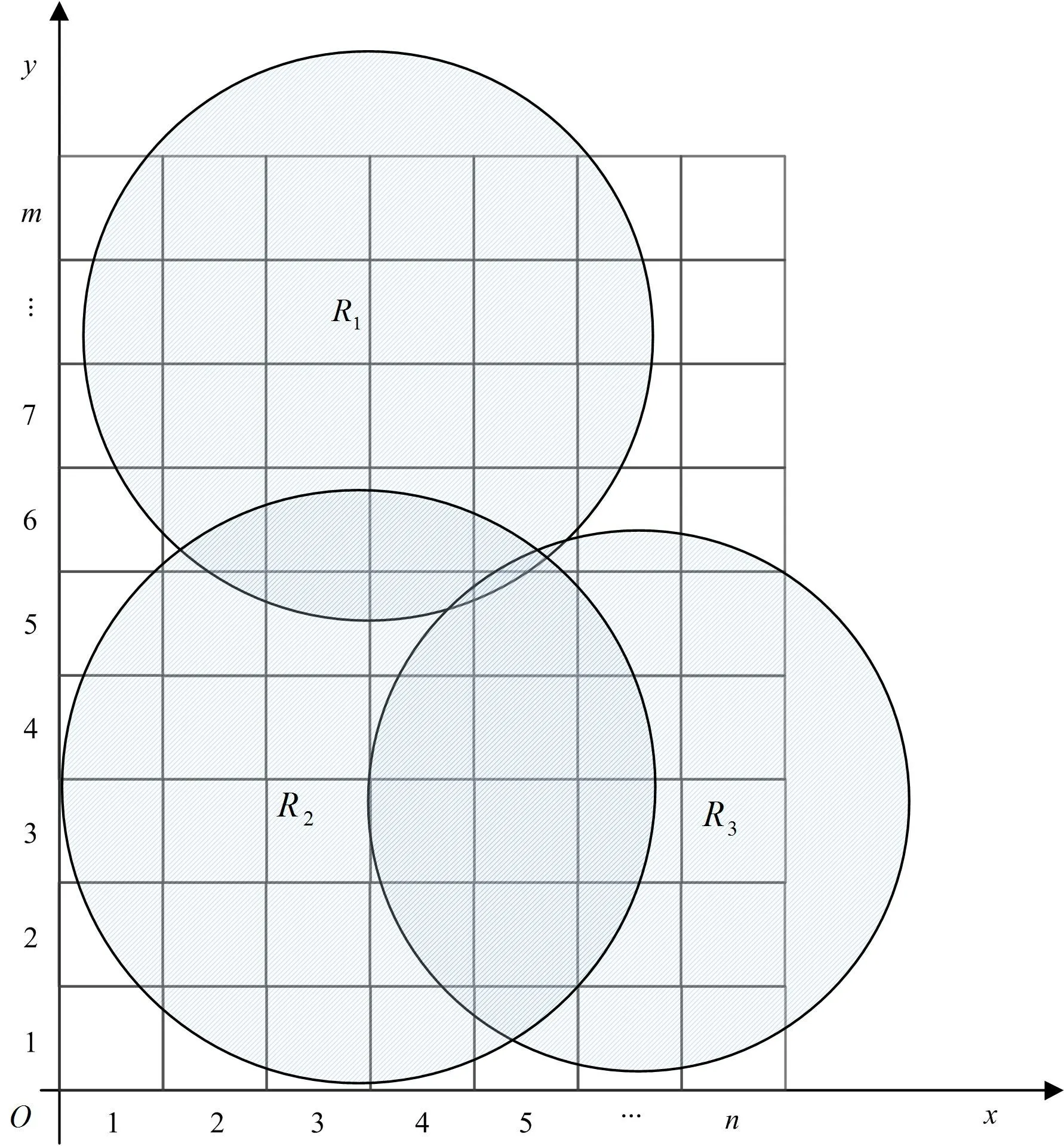
图4 雷达监视范围示意图Fig.4 Surveillance area of radars
在雷达监视范围内的空域即为能够使用的有效空域,则得到有效空域矩阵D。
再次,构建军、民航已用空域区域栅格矩阵X,Xl表示第l个空域覆盖矩阵。

分别将每个已用空域X与有效空域D相交运算,得到空域覆盖矩阵Xl。

依次计算第r(r=1,2,...,k)个雷达对栅格区域的覆盖情况,对覆盖矩阵赋值,如图5所示。
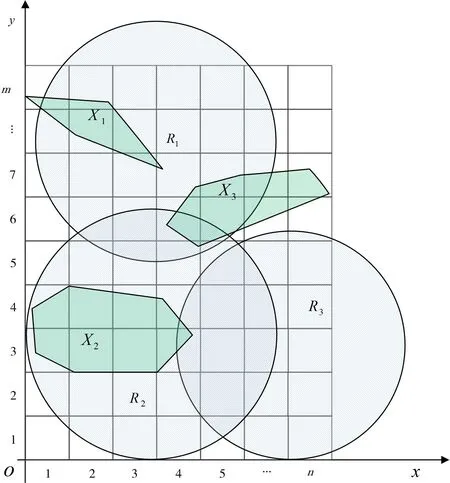
图5 海上可用空域栅格化分析示意图Fig.5 Schematic diagram of rasterization analysis of maritime available airspace
遍历空域覆盖矩阵Xl,得到海上可用栅格空域资源矩阵X,雷达监视范围内未被使用的空域资源示意图,如图6阴影填充的栅格区域所示。
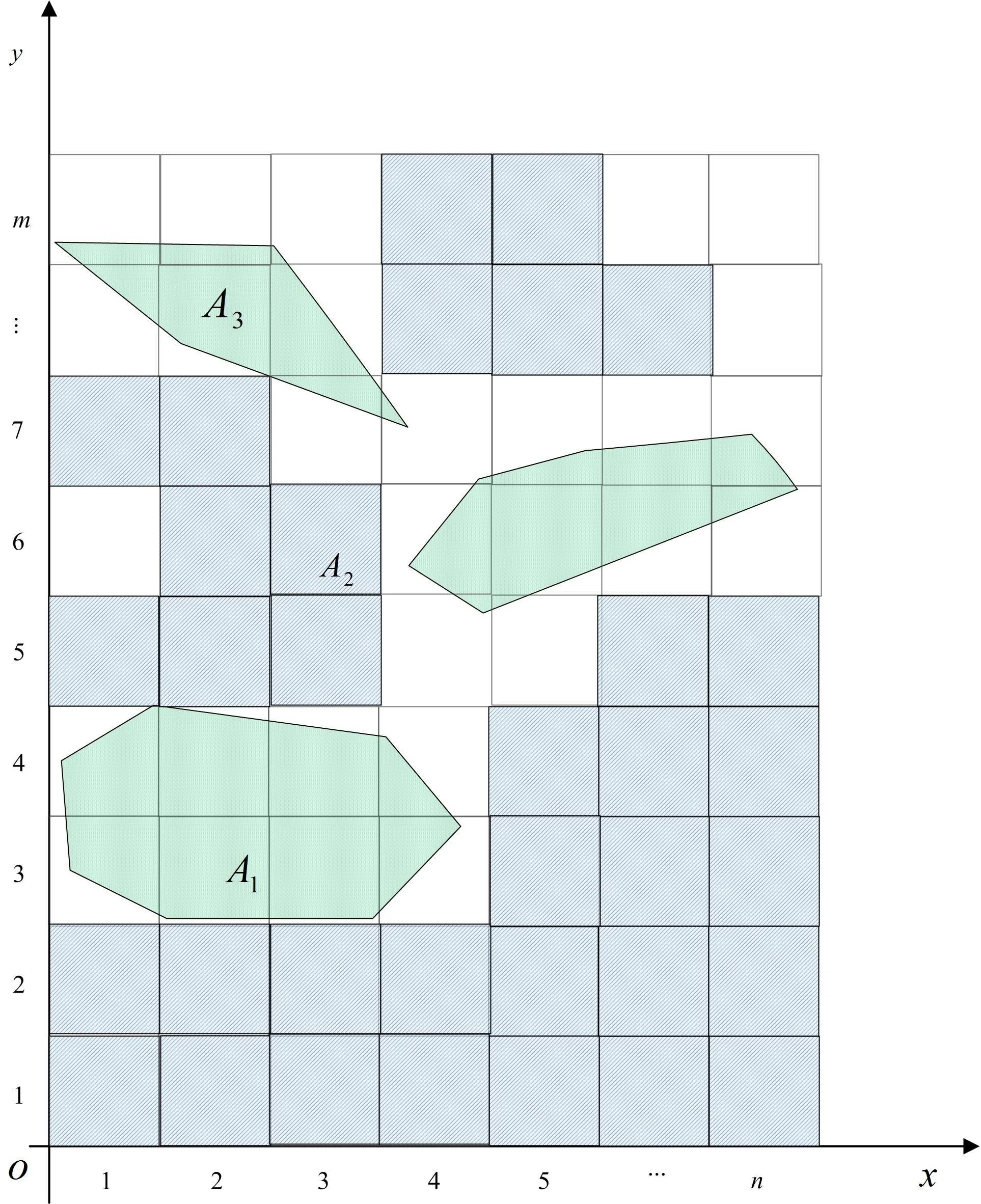
图6 雷达监视的未被使用空域资源示意图Fig.6 Schematic diagram of unused airspace resources within the radar surveillance area

最后,基于协同区域随机搜索算法得到海上所有典型飞行活动可用空域数据,具体步骤如下。
1)在海上可用栅格空域资源范围内随机分配初始位置点。
2)开始搜索,根据区域中随机产生的搜索子局部点,以直线的方式尽快找到第1个子局部点,同时在寻找子局部点的过程中持续搜索,若在该过程中搜索到目标,则终止,并告知其余搜索点目标的方位;否则前进到给定的子局部点,并继续第3步。
3)当第1 搜索点至第1 个子局部点后,在该区域中随机产生第2个子局部点。为了使选取子局部点的计算量最小,时间最快,对算法进行如下约束:
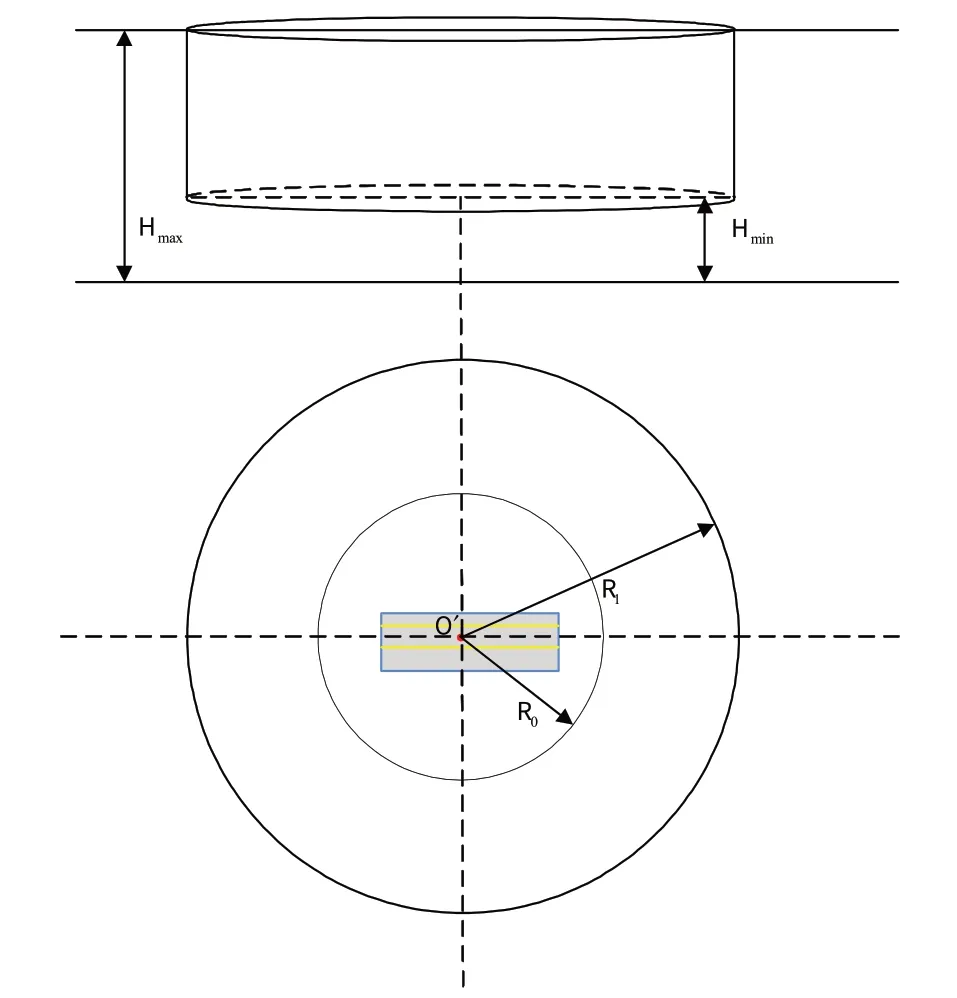
假设第i个子局部点的坐标为(xi,yi),其搜索范围为xd 式(8)中:b为子局部点数;L为常数,即该区域内下一可用空域位置距当前所有可用空域位置的最小距离。 4)在搜索目标过程中,若发现目标,则输出所有发现的目标,并在墨卡托投影坐标系中验证数据范围的准确性;若未发现目标,则结果显示未能发现目标。 为了测试该搜索算法应用于航空器海上飞行可用空域资源规划的有效性,进行如下仿真验证。 1)随机选取某海域范围,如图7 所示(图片来源于国家地图信息公共服务平台),任务区域为850 km×970 km 的矩形区域,每个栅格大小为200 m×200 m。 图7 某海区示意图Fig.7 Schematic diagram of a maritime area 2)基于墨卡托投影坐标系栅格化处理海上空域资源,如图8所示。 图8 栅格化处理海上空域资源Fig.8 Rasterized maritime airspace resources 3)将协同区域随机搜索算法用于某空域内协作搜索海上所有典型飞行活动可用空域数据的情景。针对运动单目标进行了如下理论仿真:假设航空器海上飞行起降平台的几何中心点为原点O′,以过O′点垂直于水平面的直线为轴线,R0=42 km 划设为进近等待空域,半径为R1=75 km 的圆柱面,底高距离海平面高度为Hmin=20 m ,顶高距离海平面高度为Hmax=7 500 m,构成某航空器海上飞行圆柱形空域,设定起降平台速度为18 kn,如图9所示。参数设置主要考虑了航空器海上起降平台速度、探测角度,以及航空器海上飞行空域范围。150~300 km 之间,随机产生初始目标位置点,做匀速运动,角度取( 0 °,360°) 。为验证本算法的优越性,运用传统搜索算法与本算法进行对比仿真。协同区域搜索算法仿真结果,如图10 a)所示,图中白色区域为未覆盖区域,平均仿真计算时间为56.4 s,空域利用率为78.72%;传统搜索算法仿真结果如图10 b)所示,平均仿真计算时间为76.2 s,空域利用率为72.96%。 图9 某航空器海上飞行空域结构Fig.9 Airspace structure of aircraft maritime flight 图10 某海域海上飞行可用空域资源Fig.10 Available airspace resources for maritime flight in a certain sea area 4)在搜索过程中,搜索方向始终沿其正前方,搜索时间限定为15 min,其进入点坐标初始位置在 表1 空域利用率及搜索用时Tab.1 Airspace utilization and search time 通过仿真验算得出,利用协同区域随机搜索算法可解决航空器海上飞行可用空域资源规划问题。通过与传统搜索算法对比,该算法得到的空域利用率更高,计算时间更短。相较于传统搜索算法寻找可用空域,该算法极大缩短了时间,且效果更加显著。 针对航空器海上飞行可用空域资源规划问题,本文在图形栅格化数据的基础上,设计了协同区域随机搜索算法,用于对可用空域资源进行搜寻和规划。通过算例仿真,计算出航空器海上飞行可用空域资源。仿真结果表明,该算法可有效提升空域利用率以及空域规划效率,同时能在较短时间内有效完成区域搜索任务。本文算法在理想条件下实现了对任务区域的有效覆盖搜索,但针对存在角度约束和多目标同时搜索的情况,尚需进行更加深入的后续研究。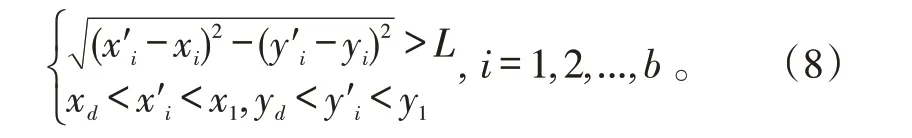
3 仿真




4 结论
