单调测度的绝对连续性

韦 叶,颜廷苏

(1.浙江信息工程学校，浙江 湖州 313000；2.湖州师范学院 理学院，浙江 湖州 313000)

0 引 言

在经典测度论[1]中，若测度μ，ν满足μ(E)=0⟹ν(E)=0，则称ν关于μ是绝对连续的，记作ν≪μ.绝对连续性是经典测度论中一个非常重要的概念.如著名的Radon-Nikodym定理：若测度ν关于σ-有限的测度μ是绝对连续的，则存在非负可测函数f,使得

由于单调测度一般不具有可加性[2]，因此经典测度的绝对连续性在单调测度论中有着不同的表现形式.例如，文献[3]引入绝对连续的9种表现形式，详细讨论了它们之间的关系；Li等引入单调测度的3种新的绝对连续性，即[E]-型、[L]-型和[R]-型绝对连续性，并建立了基于单调测度的广义Ggoroff定理、广义Lebesgue定理和广义Riesz定理，推广了在这些问题上的已有结果[4-7].

本文主要讨论单调测度的[E]-型、[L]-型和[R]-型3种绝对连续性与单调测度的条件[E](单调测度空间Egoroff定理成立的充分必要条件)、强序连续(单调测度空间Lebesgue定理成立的充分必要条件)，以及性质(S)(单调测度空间Riesz收敛定理成立的充分必要条件)之间的关系.

1 预备知识

用X表示非空集合，A为X子集构成的σ-代数，(X,A)为可测空间.如果对任意的实数α,{x|f(x)≥α}∈A,则称函数f:X(-∞,+∞)是A-可测的(简称可测的)，全体可测函数组成的集合记为F.

定义1[8-9]设实值集函数μ:A[0,∞]满足μ(∅)=0 且μ(X)>0，以及当A⊂B且A，B∈A时,μ(A)≤μ(B)，则称μ为单调测度,(X,A,μ)为单调测度空间.

单调测度的条件(E)、强序连续和性质(S)等结构特性，是在推广经典测度论中的Egoroff定理、Lebesgue定理和Riesz定理时引入的概念.由于单调测度一般不具有可加性,各种收敛性都有相应的伪性版本,因此经典的Egoroff定理、Lebesgue定理和Riesz定理在单调测度中都有4种表现形式.Egoroff定理的表现形式为:

定理1[7]设μ是定义在(X,A)上的有限单调测度,则

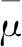
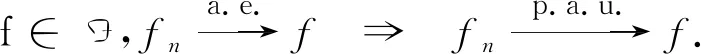
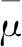
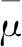
定义6[6]若对任意的集列{An}n⊂A,AnA,ν(A)=0,都有则称单调测度λ关于单调测度ν是[L]-型绝对连续的,记作λ≪Lν.

利用单调测度这3个结构特性,Li等得到了广义Egoroff定理、广义Lebesgue定理和广义Riesz定理,并统一了相应定理的各种版本[6].广义Egoroff定理陈述为：

定理2[6]设λ，ν为(X,A)上的单调测度,则下列两条等价:

(1)λ≪Eν;

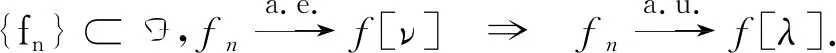
2 主要结论

下面讨论两个单调测度之间的[E]型([L]型、[R]型)绝对连续性与这两个单调测度是否满足条件(E)(强序连续、性质(S))之间的关系.

定理3存在单调测度λ、ν,使得λ和ν都不满足条件(E),但λ≪Eν.

单调测度ν定义为：

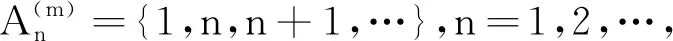
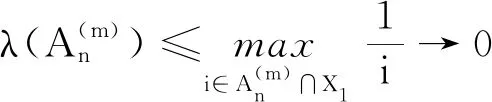
由此看出，存在{ni}和{mi}，使得

即λ≪Eν.

定理4存在单调测度λ，ν,使得λ和ν都满足条件(E),但既没有λ≪Eν,也没有ν≪Eλ.

证明设X，A如定理3，单调测度λ，ν定义为：

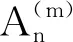
令mi=i,则易知

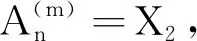
证毕.

注1还可以列举出λ满足条件(E),ν不满足条件(E),但λ≪Eν的单调测度λ,ν等.因此，λ,ν满足条件(E)与λ≪Eν和ν≪Eλ之间是相互独立的.

定理5存在单调测度λ,ν,使得λ和ν都不是强序连续的,但ν≪Lλ.

证明设为自然数集,σ-代数A=2，则定义单调测度λ,ν:A[0,∞)为:

由此看出,λ不是序连续的,因而不是强序连续的.事实上,设An={n,n+1,…},则An∅,但ν也不是强序连续的.设An={0,n,n+1,…},则An{0}且λ({0})=0,但

由于存在ν≪Lλ，事实上，设AnA,λ(A)=0,则A=∅.于是存在某个正整数n0，使得0∉An(n>n0)，则

即ν≪Lλ.

证毕.

定理6存在单调测度λ,ν,尽管λ和ν都是强序连续的,但既没有λ≪Lν,也没有ν≪Lλ.

证明设为自然数集,σ-代数A=2，定义单调测度λ、ν:A[0,∞)为:

设AnA,若λ(A)=0,则0∉A.于是，存在某个正整数n0，使得0∉An(n>n0),从而即λ是强序连续的.同理,ν也是强序连续的.

设An={1,n,n+1,…}，则An{1}且λ({1})=0,但因此ν≪Lλ不成立.同理,λ≪Lν也不成立.

证毕.

定理7存在单调测度λ,ν,使得λ和ν都不满足性质(S),但ν≪Rλ.

证明设X为全体正整数的集合,A=2X，则定义单调测度λ,ν为:

则λ,ν都不满足性质(S).

事实上,令

Ak=X({1}∪{k,2k,3k,…}),

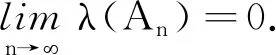
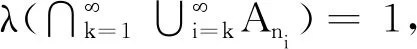
证毕.

定理8存在单调测度λ,ν,使得λ和ν满足性质(S)，且λ≪Rν,但ν≪Rλ不成立.

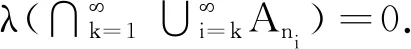
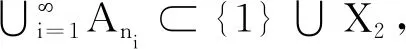
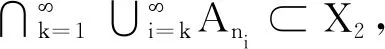
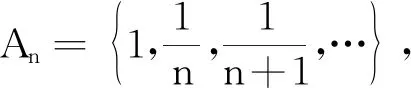
注2还可以举出其他例子说明λ，ν满足性质(S)与λ≪Rν和ν≪Rλ之间是彼此独立的.

3 结 语

本文讨论了单调测度λ和μ是否满足[E]-型([L]-型、[R]-型)绝对连续性，以及这两个单调测度是否满足条件[E]、强序连续、性质(S)之间的关系.由结果可以看出,这些条件之间没有必然的联系,是彼此独立的.今后将讨论[E]-型、[L]-型和[R]-型绝对连续性之间，以及它们与其他绝对连续性[9]之间的关系.