管道缺陷截面形状与漏磁信号关系研究
2022-11-21李志豪王宏安傅忠尧金宣杨王书生柏宝壹
李志豪,王宏安*,刘 庆,傅忠尧,金宣杨,王书生,柏宝壹
(1.山东石油化工学院 机械与控制工程学院,山东 东营 257061;2.中石化胜利石油工程有限公司钻井工艺研究院,山东 东营 257017)
油气管道作为最主要的油气资源输送方式,在服役过程中受到管道外部环境和内部输送介质的影响,不可避免产生各种缺陷和损伤,严重时可能发生油气介质泄漏甚至火灾爆炸,造成巨大人员财产损失和环境污染。管道内检测采用的无损检测方法主要有超声检测、涡流检测及漏磁检测等方法[1]。漏磁检测过程中不需要耦合剂,检测速度快,对管道内部环境影响小等优点,已经成为油气管道最常用的内检测方法,得到大范围应用[2]。
漏磁检测最重要部分是管道缺陷的量化表征,即从缺陷漏磁场信号到缺陷几何尺度的反演,就必须深入了解缺陷几何尺度与漏磁场的关系。国内外大量学者对缺陷的漏磁场进行了深入研究[3-6]。但目前在管道缺陷到漏磁场信号研究过程中,大多采用规则矩形截面的缺陷开展,而管道实际缺陷二维截面为不规则形状,在管道缺陷截面形状与漏磁场方面相关研究较少。
本文利用ANSYS有限元软件,构建漏磁检测的仿真模型,分别研究不同截面形状缺陷的漏磁场信号,分析截面形状对漏磁场信号的影响,可为漏磁检测缺陷表征提供参考,有利于进一步提高漏磁检测表征的精度。
1 二维漏磁检测有限元模型
1.1 漏磁检测原理
漏磁检测法是以铁磁性材料的高磁导率为基础的,材质均匀、连续的铁磁性材料磁化后,磁力线大部分在材料内部穿过,但当材料出现缺陷时,由于缺陷处的磁导变小,磁阻变大,磁力线的路径发生改变,磁通的大部分将先从磁阻相对较小的材料内通过;当材料内部缺陷尺寸较大或者磁感应强度较大时,缺陷处的材料难以容纳更大的磁通,就会在缺陷附近泄漏部分磁通,绕过缺陷后进入材料内部,从而形成漏磁场。
漏磁检测装备的磁化与检测部分通常包括钢刷、永磁体、背铁、传感器及其采集系统,铁磁性的管道、钢刷、永磁体及背铁构成闭合的磁回路,将管道壁磁化至饱和或者近饱和,如图1所示。若管道壁出现缺陷,磁场在缺陷附近出现泄漏,传感器及其采集系统采集记录磁场信号,通过数据分析系统对漏磁场信号进行反演从而得到缺陷几何信息。
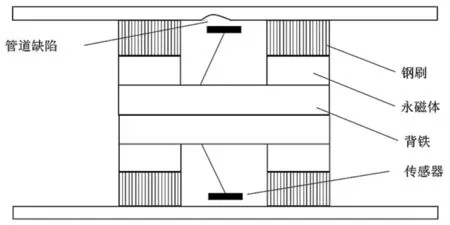
图1 漏磁检测原理图
1.2 漏磁检测有限元模型
漏磁检测过程可以看成是一个相对静态低频的电磁过程,一般认为是静磁场的问题,其本构模型可以采用安培环路定理、高斯磁通定理及电磁物质本构关系进行描述。表征模型通常包括解析模型和有限元模型。以偶极子为代表的解析模型[7],存在较多均匀性假设,实际应用中求解误差较大或不能求解,应用受到限制。有限元模型通过建立等价泛函,求解离散区域内节点的矢量磁位方程组,可以实现非线性材料复杂几何结构的漏磁检测仿真模拟,随着计算机技术发展,计算精度不断提高,得到广泛应用。
本文采用ANSYS大型通用有限元软件,建立油气管道缺陷漏磁检测有限元仿真模型,分析缺陷漏磁场信号,如图2所示。本文关注的漏磁检测磁化方式为轴向磁化,即磁力线主要沿内检测器在管道内的前进方向,故模型为漏磁检测前进过程中的一个剖面,缺陷的截面为管道轴向方向,检测器行进方向为2D模型中z坐标轴正方向,也是管道轴向,x坐标轴方向为管道轴心指向管道外壁,即为管道径向。由于漏磁检测重点关注传感器采集的漏磁场,故在缺陷附近及传感器采集路径区域进行了网格加密,用于提高漏磁场的准确性。
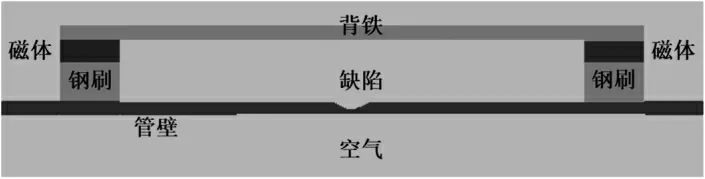
图2 漏磁检测仿真有限元模型
本文仿真模型管道壁厚为16 mm,利用ANSYS求解器进行求解计算,磁力线分布如图3所示,从结果可以看出,在油气管道壁缺陷附近内表面和外表面邻近区域出现了明显的漏磁通。
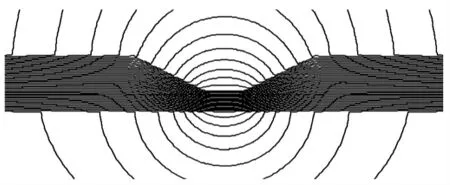
图3 缺陷磁力线分布
漏磁检测过程中传感器存在一定的提离,在这里提离值按4 mm考虑,提取结果中对应漏磁场信号。针对传统矩形缺陷,建立一组缺陷,长度L分别为10、30、50、70、90 mm,深度为11 mm,即深度为69%t(t为壁厚)。缺陷长度不同,深度相同,在提离4 mm处的漏磁信号如图4所示。从结果可以看出,缺陷深度保持不变,缺陷长度不断变大的情况下,漏磁信号径向分量的波峰和波谷间距不断增加,轴向分量波峰值不断衰减,当缺陷长度为30 mm时出现双波峰,并随着缺陷长度增加,2个波峰之间的间距不断增加。
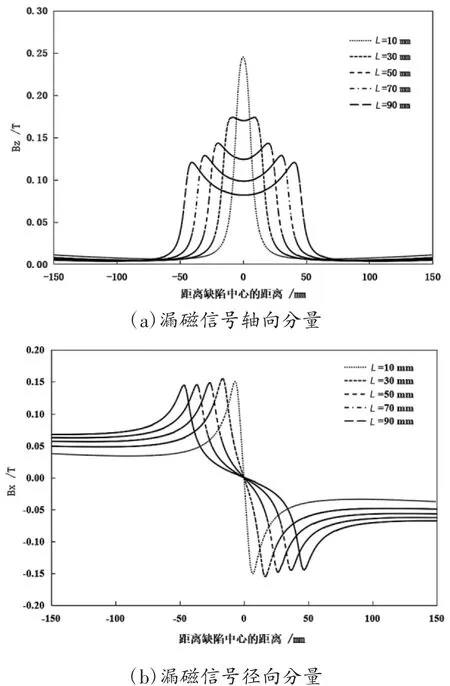
图4 不同长度的矩形缺陷漏磁信号
采用矩形截面,建立一组缺陷,深度D分别为2、4、6、8、10 mm,即深度从13%t到63%t变化,缺陷长度为30 mm。缺陷深度不同,长度相同,提取漏磁信号如图5所示。可以看出,缺陷长度不变,缺陷深度不断增加的情况下,漏磁信号的轴向分量和径向分量幅值在不断增大。
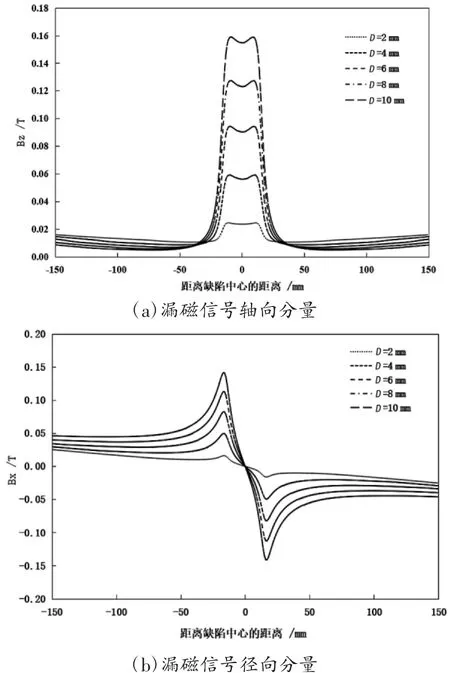
图5 不同深度的矩形缺陷漏磁信号
2 缺陷截面形状与漏磁信号关系分析
2.1 梯形截面缺陷对漏磁信号影响分析
管道腐蚀缺陷产生通常是一个缓慢的过程,因此管道缺陷截面通常为不规则的,实际缺陷截面边缘一般不会是直角,在这里采用梯形截面进行模拟。管道壁厚16 mm、缺陷长度30 mm、缺陷深度6 mm(38%t),建立3个等腰梯形截面缺陷,同时引入矩形截面缺陷进行对比。3个等腰梯形截面区别在于,梯形斜边的斜率不同,斜率K分别为0.5、1和2,如图6所示。分别计算4个缺陷的漏磁场,在提离值4 mm处提取信号的轴向分量和径向分量,如图7所示。
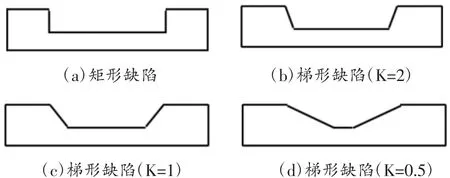
图6 缺陷截面形状
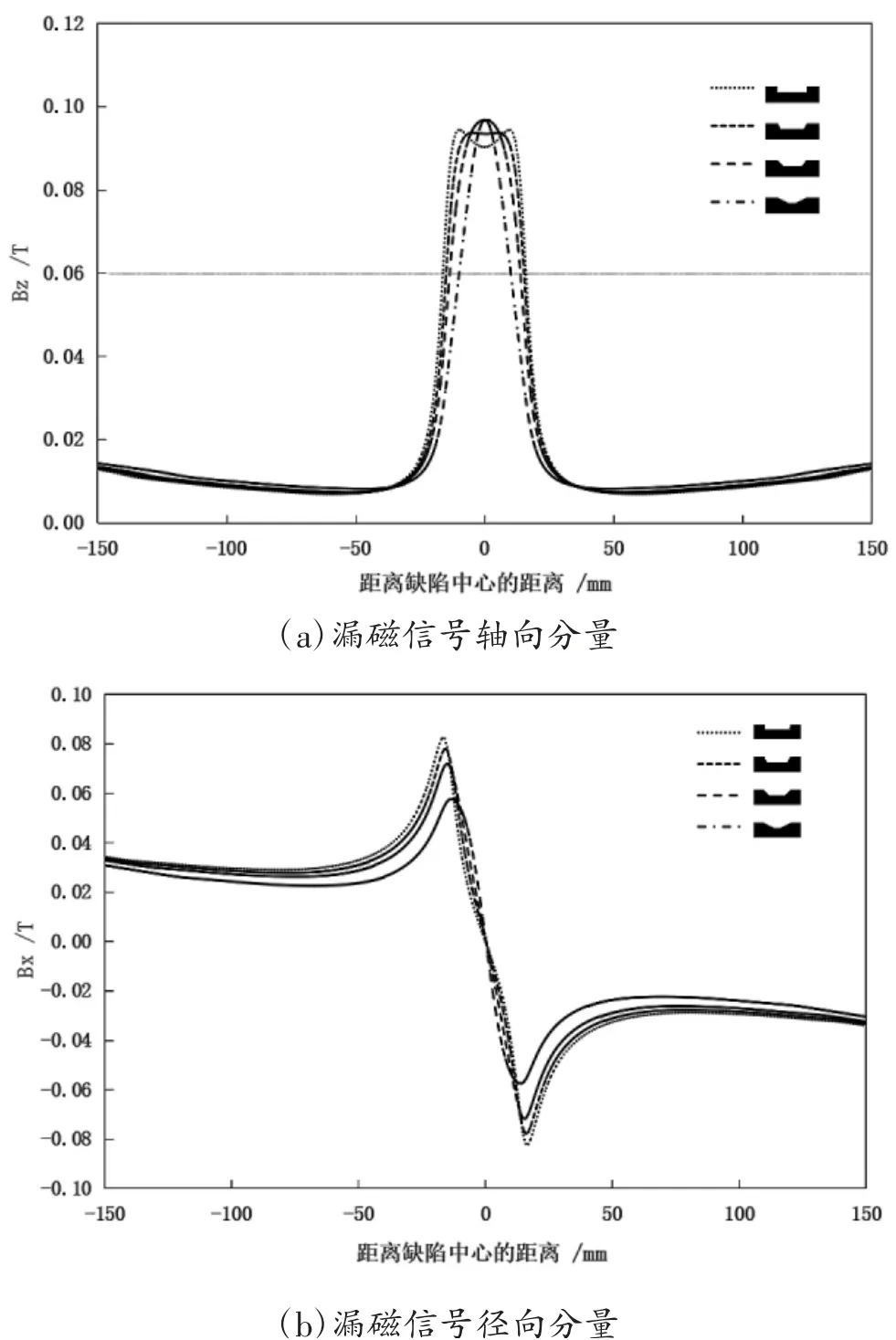
图7 梯形截面缺陷漏磁信号对比
从图7可以看出,对于同一尺度缺陷,径向分量峰值和谷值的绝对值及峰谷值在截面为矩形时最大,可以认为矩形截面为梯形截面斜边斜率为无穷大时的特殊情况,那么径向信号绝对值随着梯形截面斜率K减小而减小;从轴向分量结果可以看出,矩形缺陷出现了双波峰,斜率K为2的梯形缺陷波峰较为平坦,具有双波峰的趋势,斜率K为1和0.5的梯形缺陷未出现双波峰现象,波峰值几乎相同;取0.06 T做一条水平参考线,可以看出波峰整体宽度随着斜率K的减小而减小。
总体来说,缺陷截面形状斜边斜率越大,缺陷截面变化越剧烈,轴向信号波峰宽度越大,易形成双波峰现象,径向信号绝对值随斜率增大而增大。在漏磁数据反演中,这4个缺陷的漏磁信号进行等效尺度量化分析,应得到相同的长度和深度结果,但信号之间存在明显差异,故缺陷反演算法提取特征时应充分考虑截面形状的影响,进行修正,避免由于缺陷截面不同造成缺陷尺寸量化出现较大偏差。
2.2 阶梯形截面缺陷对漏磁信号影响分析
管道腐蚀缺陷产生与管道输送介质的性质有一定关系,不同时期的管道介质对腐蚀影响存在差异,因此管道缺陷截面也可能是阶梯形状,建立阶梯截面的缺陷,并引入矩形缺陷和梯形缺陷进行对比。管道壁厚16 mm,缺陷长度50 mm、缺陷深度10 mm(63%t)。假设阶梯缺陷是2个轮次腐蚀造成的,第一轮次腐蚀深5 mm,缺陷长度50 mm,第二轮次在腐蚀深度5 mm的基础上再腐蚀5 mm深度,腐蚀长度为20 mm。分别计算3个缺陷的漏磁场,在提离值4 mm处提取信号的轴向分量和径向分量,如图8所示。
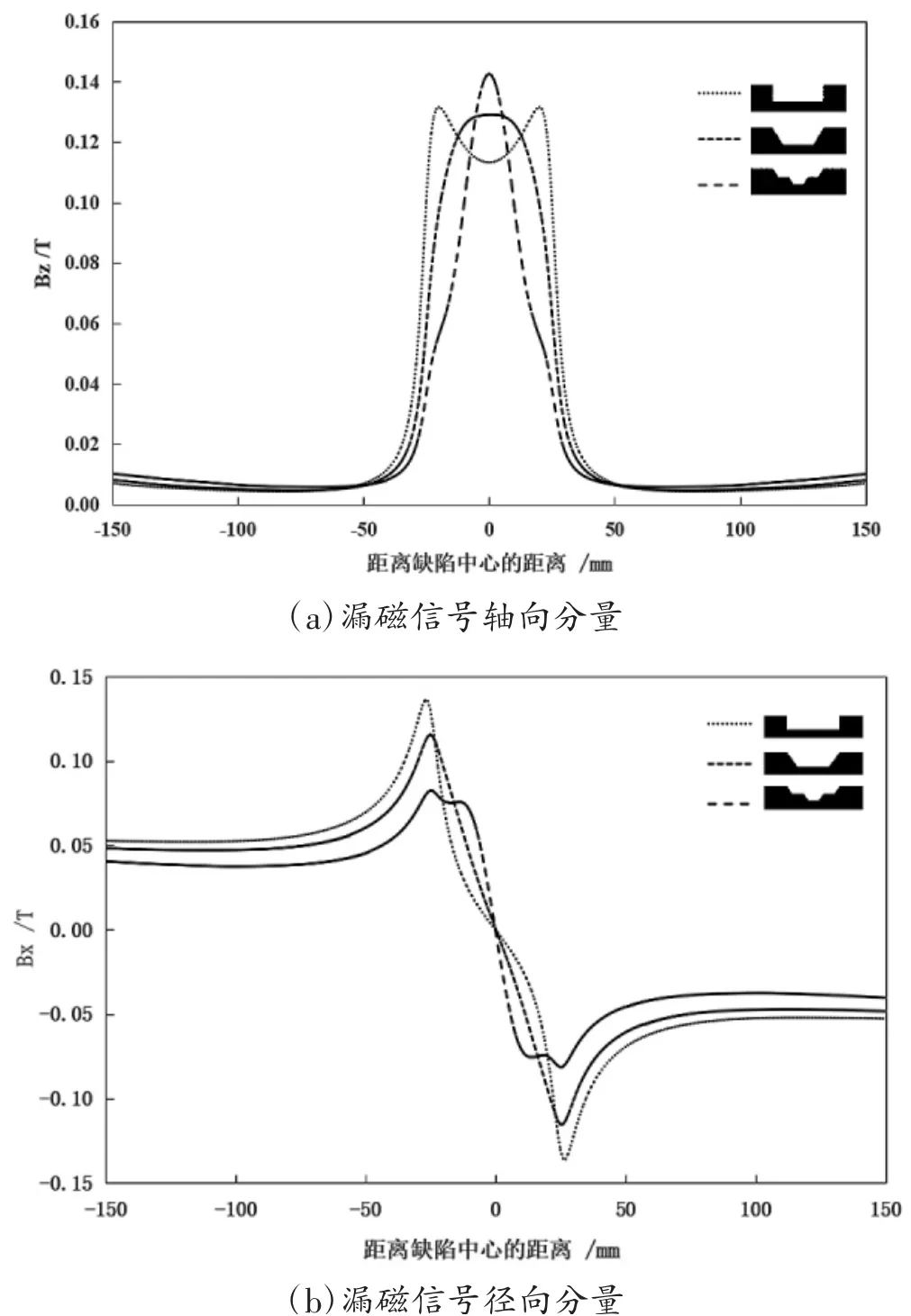
图8 阶梯形截面缺陷漏磁信号对比
从图8可以看出,对于轴向信号分量,矩形缺陷出现双波峰,梯形缺陷和阶梯缺陷为单波峰,阶梯缺陷的波峰值最大,波峰宽度来看,矩形缺陷最大,阶梯缺陷最小;径向信号的绝对值方面,矩形缺陷最大,阶梯缺陷最小,其中阶梯缺陷可以明显发现信号呈现阶梯状,反映了2个轮次的腐蚀过程。
总体来说,3个缺陷信号在等效尺寸反演时应得到同样的缺陷长度和深度,故在缺陷等效尺寸量化的特征值提取需考虑信号之间的差异。同时发现径向信号对缺陷边缘反映较为敏感,在开展截面形状反演时,应加大径向信号的特征权重。
3 结束语
(1)通过对梯形截面形状漏磁信号研究,发现缺陷漏磁信号径向分量绝对值随着梯形截面斜率减小而减小,轴向信号波峰宽度随着斜率增大而增大,同时斜率增加易造成双波峰的出现。
(2)对于多轮次腐蚀形成的阶梯状缺陷,相比矩形缺陷和梯形缺陷,轴向信号波峰宽度较小,径向信号幅值也较小,同时径向信号可近似反映阶梯状缺陷阶梯边缘,对缺陷截面形状反演可提供较多信息。
