风力发电变桨距模糊自适应PID控制
2022-11-21张继勇嵇仁君马一鸣杨茂朕
张继勇,嵇仁君,马一鸣,杨茂朕,王 凯
(扬州大学 电气与能源动力工程学院,江苏 扬州 225009)
由于风力发电的巨大潜能,世界各国都很注重对风力发电技术的研究,风力发电控制技术也不断取得突破性进展,原先被广泛应用的定桨距控制也被逐渐淘汰,由变桨距控制取代。定桨距控制本身存在着一定的缺陷,在实际风速过大时,其桨距角保持不变,只能依靠叶片进入失速状态,以此使升力不随风速的增大而增大,达到限制发电机输出功率的目的,但这对叶片的制造工艺有着很高的要求,还会出现超负荷现象,让风力发电机组的疲劳损坏加速。而变桨距控制技术可以使桨距角随着风速的变化而改变,能够使风机在恒功率状态下运行,如今已被世界各国广泛应用。
吴俊鹏等采用传统PID控制器,提前设定好PID控制器的kp,ki,kd参数,以此来控制桨距角的大小,但在运行过程中,PID控制器的参数是固定不变的。目前,传统PID控制器因其结构简单及能够有效消除稳态误差的特点,在变桨距控制方面仍被广泛应用,但风速随时都会变化,一组固定的PID参数已经不能满足要求,PID参数需要适应风速的变化。倪焕山等面对兆瓦级风电机组特性,提出模糊智能变桨距控制算法,以额定功率和实际功率的偏差值和偏差值变化率为输入量,控制桨距角变化。而模糊控制虽然可以很好地面对外界扰动,但在稳态误差消除方面表现出不足。本文提出模糊自适应PID控制,该控制方案结合了传统PID控制和模糊控制两者的优点,在抗干扰和稳态误差消除方面都能达到理想的效果,可以有效地缩短调节时间,提高系统的鲁棒性和稳定性。
1 风力发电机组变桨距模型
风力发电机组通过风轮轮毂上的叶片和发电机,将动能转换为电能,在输入风速v的作用下,风轮的吸收功率和气动转矩为
式中:Pr为风轮的吸收功率;Tr为风轮的气动转矩;Cp为风能利用系数;Cr为气动转矩系数;λ为叶尖速比;β为桨距角;ρ为空气密度;R为风轮半径。
叶尖速比λ是叶尖转速与输入风速的比值,其表达式为
式中:wm为叶片的角速度。
风能利用系数Cp是叶尖速比λ和桨距角β的函数,常用的经验公式为
与λ、β函数关系图如图1所示。
由图1可知:
(1)桨距角β的值不同时,其所对应的最佳风能利用系数Cpmax也不同,当桨距角为0°时,最佳风能利用系数Cpmax达到最大,而每条曲线的Cpmax所对应的叶尖速比λ为最佳叶尖速比λopt。
(2)当实际风速大于额定风速时,可以增加桨距角β值,这样曲线所对应的Cp值都会有所下降,风力发电机组整体的风能利用系数减小,风力机对风能的利用率就会下降,发电机的输出功率就不会随着风速的提高而增加,而是维持在额定功率附近。
2 模糊自适应PID控制器的设计
2.1 模糊自适应PID控制方案
为了使风力发电机能够维持恒定功率输出,风力机的风能利用系数就需要随着风速的变化而变化,这就可以通过对桨距角大小的实时调节来实现。
由于风能的随机性和突发性,传统PID控制器固定的kp,ki,kd参数并不能满足系统的要求,而模糊自适应PID控制能够根据反馈,实时调节kp,ki,kd参数,提高系统的鲁棒性和抗干扰能力。选择可以对被控对象接下来的变化进行预判的二维模糊控制器为主控制器,其控制效果良好。
本文选取发电机实际转速和额定转速的偏差e和偏差变化率ec作为二维模糊控制器的输入变量,在经过模糊化描述,模糊规则表建立,模糊推理和去模糊化等步骤后,得到模糊PID自适应系统kp,ki,kd参数的调节量Δkp,Δki,Δkd,实时调节参数,使系统在风速变化时能维持恒功率输出,模糊自适应PID控制器的结构如图2所示。
2.2 模糊自适应PID控制器的设计
2.2.1 输入量和输出量的模糊化描述
确定控制系统的输入量为发电机实际转速和额定转速的偏差值e和偏差变化率ec,输出量为PID参数的调节量Δkp,Δki,Δkd,定义输入变量e,ec的离散论域为{-3,-2,-1,0,1,2,3},其中偏差e的基本论域为[-30,30],量化因子Ke=0.1,
偏差变化率ec的基本论域为[-3,3],量化因子Kec=1,输出量Δkp,Δki,Δkd的离散论域和e,ec一致。
在选择隶属函数时,为了达到不同的控制效果,选择的隶属函数形状也不同。为了避免桨距角控制死区的出现,使模糊自适应PID控制器可以随着风速的变化实时调整桨距角,以此让风力发电机组处于额定功率状态,本文选择了三角形隶属函数,这样不仅可以提高控制精度,还可以对隶属函数论域覆盖程度进行调节,使风力发电机组输出达到最优。
2.2.2 建立模糊化规则
通过分析发电机实际转速和额定转速的偏差和偏差变化率,对桨距角进行实时调节。针对转速偏差值较大的情况,把尽快消除偏差作为主要目的,输出相应的控制量;当偏差值较小时,以维持稳定为主要目的,输出相应控制量。
在整定PID参数时,在不同时间,kp,ki,kd在系统中发挥的作用也会随着偏差值和偏差值变化率的变化而产生改变,对3个参数的要求如下。
(1)在偏差值e较大时,可以取较大的kp值以加快系统的响应速度,如果没有对系统的积分作用加以限制,会出现积分饱和现象,从而导致超调量过大,所以一般会选择取Δki=0以避免这种情况。
(2)在偏差值e和偏差值变化率ec中等大小时,可以取较小的kp值,适中的ki值和kd值,这样既可以使系统响应具有较小的超调,又可以保证系统的响应速度。
(3)在偏差值e值较小即将接近于设定值时,可以增加kp和ki的值,而kd的取值对于系统面对干扰能否有良好的控制效果尤为重要,在偏差值变化率ec较大时,应该取较小的kd值,在偏差值变化率ec较小时,应该取较大的kd值。
根据上述要求建立参数Δkp,Δki,Δkd的模糊调节规则表,调节规则表见表1—表3。
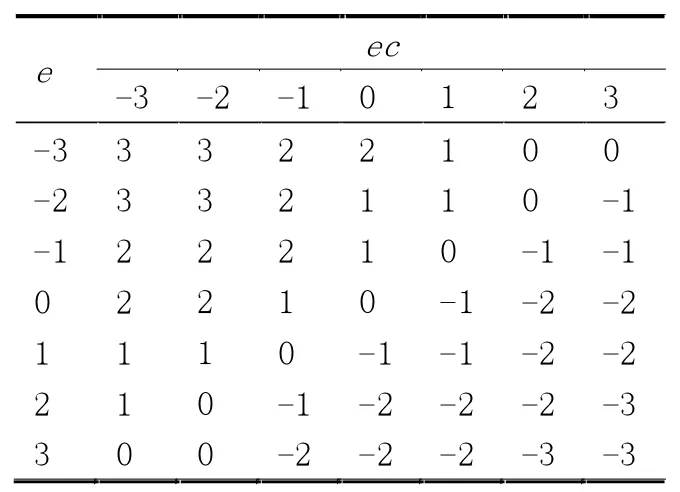
表1 Δkp的模糊规则表
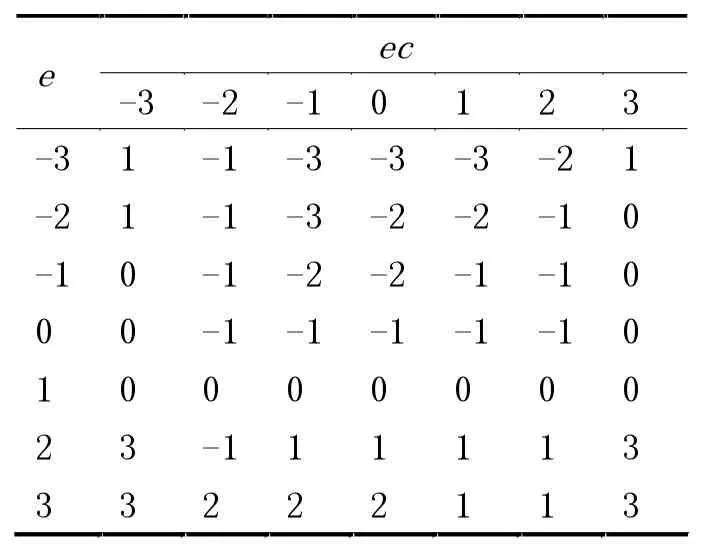
表2 Δki的模糊规则表
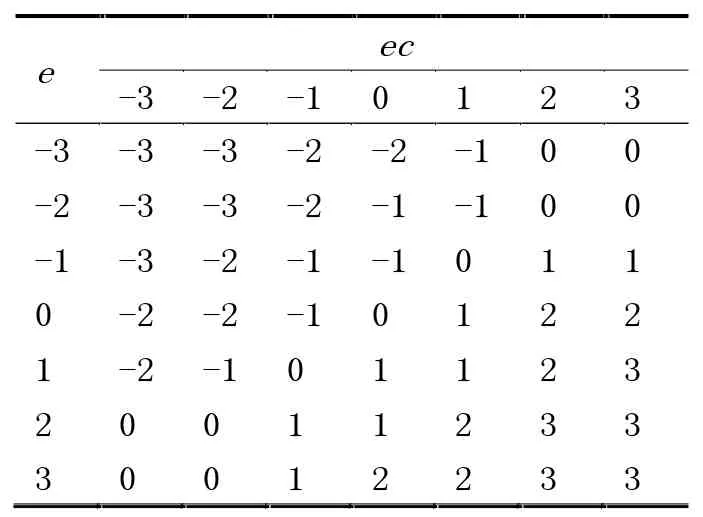
表3 Δkd的模糊规则表
2.2.3 模糊推理
根据模糊自适应PID的输入的模糊量,基于设置的模糊关系方程,获得的输出模糊控制量,重复上述操作,得到所有可能的输出值,并建立模糊控制表,之后可以采用查表的方法确定相应的输出值,这种方法就是CRI查表法,其具有操作简单、实时性好的优点。
2.2.4 去模糊化
经过模糊推理后,得到的结果是一个模糊集,模糊集里的控制量信息繁杂,要想从中得到一个精准清晰的控制量,需要对其进行去模糊化处理。本文选用的是加权平均法,该方法将模糊集里的多个元素都考虑在内,通过调整加权系数来对系统的响应特性进行改善,灵活性较大,控制效果较好。
通过获取去模糊化的输出控制量,可以获得kp,ki,kd参数的调节量
式中:kp0,ki0,kd0是kp,ki,kd的初始值,根据调节量,可以实时调节模糊自适应PID参数,使风力发电机组维持额定功率状态。
3 系统仿真
3.1 仿真模型
风力发电系统模型由风速模型、风力机、永磁同步发电机、变桨距控制器和电网等部分构成。采用基于发电机转速偏差和偏差变化率的模糊自适应PID控制方式,在风速过大时,通过增大桨距角的大小,让风力发电机组得到一个适合的风能利用系数,以此使风力机的输出功率恒定,在这个仿真模型中,风机的额定功率设置为6.5 kW,额定风速设置为12 m/s。
3.2 仿真结果
3.2.1 阶跃风速仿真结果
首先采用阶跃风速模型对风电系统进行仿真运行,阶跃风速曲线如图3所示。
当风速为12 m/s,此时的风速为额定风速,桨距角为0°,输出功率为额定功率,风力机对风能的利用率达到最大,当风速大于额定风速时,变桨距控制器开始工作,会控制桨距角增大,让风力机对风能的利用率下降,使发电机的输出功率在额定功率附近,输出功率波形图如图4所示,可以看出风力发电机组在风速等于及大于12 m/s时,基本维持在额定功率状态。
3.2.2 随机风速仿真结果
由于阶跃风速在现实中几乎不存在,所以采用随机风速模型,该风速模型最小风速12 m/s,最大风速20 m/s,平均风速为16 m/s,利用其对风力发电机组进行仿真运行,风速模型如图5所示。
输出功率如图6所示,从图6中可以看出发电机的输出功率在额定功率附近。
4 结论
本文在考虑传统PID控制和模糊控制的优缺点后,提出模糊自适应PID控制,通过对发电机实际转速和额定转速偏值e和偏差值变化率ec的不断检测,实时调整kp,ki,kd值,提高系统地动态性能,经过仿真,发现风力发电机组在阶跃风速和随机风速模型下,仍然能使输出功率维持在额定功率附近,达到恒功率输出的目的,具有较好的适应性和鲁棒性。
