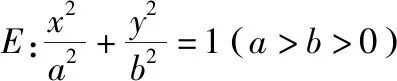顺应“三新”研究趋势 探索变式教学模式——“数学经典试题及变式”征集活动解析几何母题组精选

一、求圆锥曲线的方程

吉林 韩兆峰

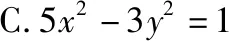
【试题分析】考查知识：本题主要考查双曲线的标准方程及离心率，解题关键在于理解双曲线的定义及标准方程中相关参数之间的等量关系与几何意义.

解题方法：定义法，待定系数法，运算求解能力及数形结合、化归与转化思想.

综合拓展：引伸到点、直线、圆与圆锥曲线的位置关系，研究圆锥曲线的方程问题.

【答案】B

吉林 韩兆峰

【变式1】(知识变式)转化为双曲线的一部分

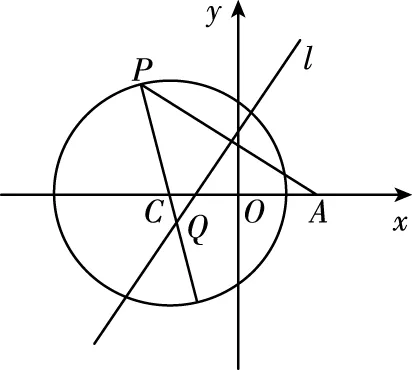
如图,P是圆C：(x+3)2+y2=25上任意一点，定点A(3,0)，线段AP的垂直平分线l和直线CP相交于点Q，当点P在圆C上运动时，点Q的轨迹方程是______.

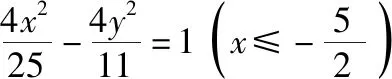
吉林 韩兆峰

【变式2】(方法变式)变“双曲线”背景为“椭圆”背景,利用弦长处理参数问题

甘肃 彭长军

【变式3】(方法变式)改变确定双曲线的条件

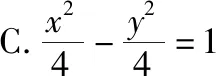
【答案】D

吉林 韩兆峰

【变式4】(综合变式)把离心率转化为渐近线与圆的关系

经过点(2,1)，且渐近线与圆x2+(y-2)2=1相切的双曲线的标准方程为( )

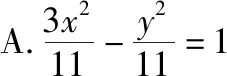
【答案】A

吉林 韩兆峰

【变式5】(综合变式)从向量的角度描述动点

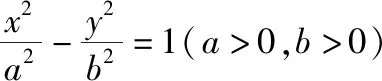
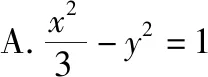
【答案】D

甘肃 彭长军

【变式6】(综合变式)双曲线中融入圆

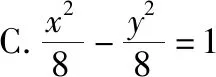
【答案】A

湖北 冯爱龙

【母题2】下列命题为真命题的序号是________．

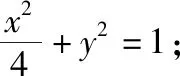
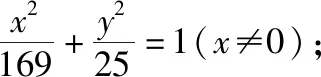
(4)已知点C的坐标为(2,2).过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线CB与y轴交于点B，设点M是线段AB的中点，则点M的轨迹方程为x+y-2=0.

【试题分析】考查知识：求动点的轨迹的几种常用方法，直线、圆、椭圆等曲线的定义与标准方程.

解题方法：求圆锥曲线标准方程“先定型，后计算”.所谓“定型”，就是确定曲线焦点所在的坐标轴的位置；所谓“计算”，就是指利用待定系数法求出方程中的k,a2，b2，p等参数的值．

综合拓展：从代数与几何两方面认识圆锥曲线的定义与性质.

【答案】(1),(2),(4)

河北 赵伟娜

【变式1】(知识变式)给出方程看曲线

(2020·新高考Ⅰ卷·9)已知曲线C：mx2+ny2=1.则( )

A．若m>n>0，则C是椭圆，其焦点在y轴上

D．若m=0，n>0，则C是两条直线

【答案】ACD

河北 赵伟娜

【变式2】(知识变式)变换条件，利用不同方法求圆锥曲线的方程

在平面直角坐标系xOy中：

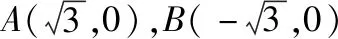
在①②③这三个条件中任选一个，求动点P的轨迹方程.

注：如果选择多个条件分别解答，按第一个解答计分

湖北 冯爱龙

【变式3】(方法变式)向量作为数形结合的典型工具，将几何条件数量化

已知点P(2,2)，圆C:x2+y2-8y=0，过点P的动直线l与圆C交于A,B两点，线段AB的中点为M，O为坐标原点．求动点M的轨迹方程.

【答案】(x-1)2+(y-3)2=2

湖北 冯爱龙

【变式4】(综合变式)利用圆的对称性、平行线转化得到角的等量关系，进而转化为点的坐标，根据面积关系转化为线段关系，进而转化|EA|+|EB|=|EA|+|ED|=|AD|为定值

设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.证明|EA|+|EB|为定值,并写出点E的轨迹方程.

湖北 冯爱龙

【变式5】(综合变式)抛物线的定义与焦半径公式，点的坐标与点到直线的距离的转化，用向量的数量积知识转化垂直条件

设抛物线C：y2=2px(p>0)的焦点为F，点M在C上，|MF|=5.若以MF为直径的圆过点(0,2)，则C的方程为( )

A．y2=4x或y2=8xB．y2=2x或y2=8x

C．y2=4x或y2=16xD．y2=2x或y2=16x

【答案】C

甘肃 彭长军

【母题3】(2022·全国甲卷理·20(1))设抛物线C:y2=2px(p>0)的焦点为F，点D(p,0)，过F的直线交C于M,N两点，当直线MD垂直于x轴时，|MF|=3,求C的方程.

【试题分析】考查知识：抛物线的定义、性质及标准方程.

解题方法：化归与转化思想的应用.

综合拓展：围绕抛物线定义的综合问题.

【答案】y2=4x

甘肃 彭长军

【变式1】(知识变式)将垂直变为长度相等

设抛物线C:y2=2px(p>0)的焦点为F，点D(p,0)，过F的直线交C于M,N两点，若|MF|=|MD|=3，求C的方程.

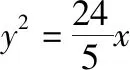
甘肃 彭长军

【变式2】(知识变式)抛物线中嵌入向量数量积

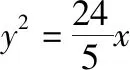
甘肃 彭长军

【变式3】(方法变式)将垂直变为不垂直

甘肃 彭长军

【变式4】(方法变式)抛物线中嵌入最值

设抛物线C:y2=2px(p>0)的焦点为F，过F的直线交C于M,N两点，当原点O到直线MN的距离最大时，|MF|=3,求C的方程.

【答案】y2=6x

甘肃 彭长军

【变式5】(综合变式)改变题设条件

【答案】y2=3x

二、圆锥曲线离心率的取值范围问题

甘肃 彭长军

【试题分析】考查知识：椭圆的标准方程与性质，直线与圆的位置关系及简单几何性质，点到直线的距离公式以及点与曲线的位置关系等.

解题方法：推理计算法.

综合拓展：基于上述知识的综合问题.

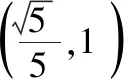
甘肃 彭长军

【变式1】(知识变式)把椭圆换成双曲线

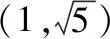
甘肃 彭长军

【变式2】(知识变式)把圆换成抛物线

甘肃 彭长军

【变式3】(知识变式)把椭圆换成双曲线，同时把圆换成抛物线

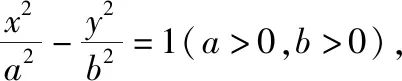
甘肃 彭长军

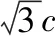
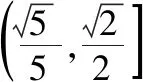
河北 赵伟娜

【试题分析】考查知识：椭圆与双曲线的定义及其简单几何性质.

解题方法：数形结合、方程与不等式思想的应用.

综合拓展：基于求离心率的取值范围问题.

河北 赵伟娜

【变式1】(知识变式)焦点三角形顶角发生变化，由特殊角变为非特殊角

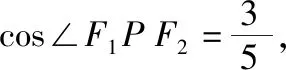
河北 赵伟娜

【变式2】(综合变式)变换角度关系为线段长度关系，利用二次函数求取值范围

(2022·高三模拟·8)已知椭圆C1和双曲线C2有公共的焦点F1，F2，C1和C2在第一象限相交于点P，且|F1F2|=2|PF2|，设C1与C2的离心率分别为e1，e2，则e2-e1的取值范围是( )

【答案】D

甘肃 彭长军

【变式3】(综合变式)将范围问题变为最值问题

【答案】C

陕西 韩红军

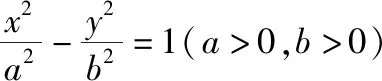
A.(2，+∞) B．(1，2)

【试题分析】考查知识：双曲线的离心率，双曲线的定义及其性质.

解题方法：利用正弦定理的边角互化以及双曲线的定义解不等式，考查数形结合思想.

综合拓展：基于双曲线离心率的综合问题.

【答案】D

陕西 韩红军

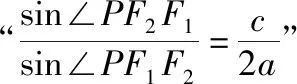
【答案】B

陕西 韩红军

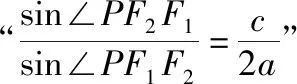
陕西 韩红军

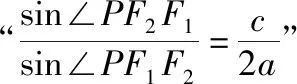
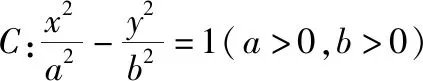
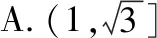
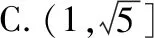
【答案】C

陕西 韩红军

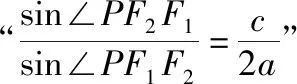
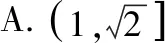
【答案】C

广东 龙宇

【试题分析】考查知识：椭圆的定义，直线斜率的意义，直线与椭圆的位置关系，轴对称的性质.

解题方法：利用基本量法获得椭圆三个参数间的关系从而获得离心率，根据椭圆的第三定义求解，利用伸缩变换将椭圆化为圆，利用圆的性质求解，再结合伸缩变换的性质确定椭圆的离心率.

综合拓展：通过解题培养学生的推理论证能力，数形结合等数学思想，渗透逻辑推理以及直观想象等数学核心素养.

【答案】A

山西 李小丽

【变式1】(知识变式)将“焦点在x轴上的椭圆”变为“焦点在y轴上的椭圆”

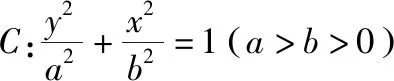
【答案】A

山西 李小丽

【变式2】(知识变式)将“两顶点”变为“关于原点对称的两点”

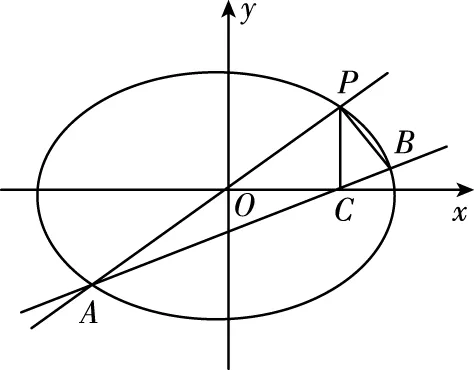
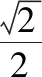
江苏 沈雪明

【变式3】(知识变式)从椭圆迁移到双曲线

【答案】D

辽宁 蔡明天

【变式4】(知识变式)关于x,y轴对称互变

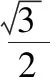
四川 王昌林

【变式5】(方法变式)通过几何分析，求出或用未知数表示出a，c的值，求出离心率

【答案】A

江苏 沈雪明

【变式6】(方法变式)由原题过顶点的两直线斜率乘积为定值，转化为过焦点的两直线的斜率为定值

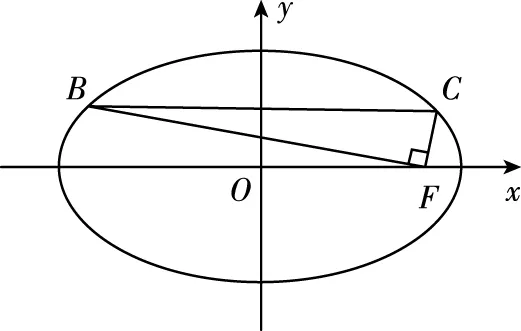
山西 李小丽

【变式7】(综合变式)将“母题中椭圆上的点A，P，Q”均变为“椭圆上一般的三点”