探究真题命题导向 深化创新思维发展——2022年创新性高考试题及变式选登

山东 贵州 尹承利 李 寒 苏 福

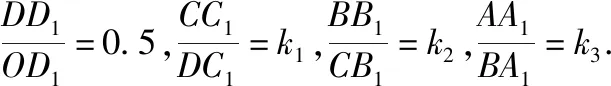
图1

图2

A.0.75 B.0.8 C.0.85 D.0.9

【参考答案】D

【创新点说明】本题结合数学学科知识，展示数学文化，感受数学之美，取材于中国古建筑物，以中国古代建筑中的举架结构为背景，考查学生综合应用等差数列、解析几何、三角函数等基础知识解决实际问题的能力，让学生领略中华民族的智慧和数学研究成果，进一步树立民族自信心和自豪感，培育爱国主义情感，体现了高考试题的创新性原则.

【变式】第41届上海世博会的中国馆——“东方之冠”气势磅礴，令人印象深刻.该馆以“东方之冠，鼎盛中华，天下粮仓，富庶百姓”为设计理念，代表中国文化的精神与气质.其形如冠盖，层叠出挑，制似斗拱.它有四根方柱，托起斗状的主体结构，上方的“斗冠”类似一个倒置的正四棱台，若“斗冠”的高、“斗冠”侧面的高和中国馆的总高度构成公差约为17 m的等差数列，且“斗冠”侧面的“坡比”约为0.78，“斗冠”侧面的高约为44 m，则上底面边长与下底面边长的差约为( )

A.45 m B.54 m C.69 m D.76 m

【参考答案】C

【解题思路】如图为中国馆“斗冠”的直观图，

【变式说明】中国馆融合了中国古代营造法则和现代设计理念，诠释了东方“天人合一，和谐共生”的哲学思想，展现了艺术之美、力度之美、传统之美和现代之美，是对中国文化的最好表达.本题以“中国馆”为背景，融合等差数列、立体几何、坡比等知识及列方程组计算的方法，知识交汇命制，考查直观想象、逻辑推理及数学建模等数学核心素养，尤其本题引入初中学习的“坡比”概念，体现了对知识的基础性和全面性的考查要求.

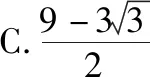
【参考答案】B

【创新点说明】本题结合学科知识，展示数学文化，取材于我国古代科学家沈括的杰作《梦溪笔谈》，以沈括研究的圆弧长计算方法“会圆术”为背景，让学生直观感受我国古代科学家探究问题和解决问题的过程，引发学生的学习兴趣，体现了高考试题的创新性原则.

【创新点说明】本题结合学科知识，展示数学文化，以“南宋数学家秦九韶发现的从三角形三边求面积的‘三斜求积’方法”为背景，在《普通高中课程标准实验教科书A版必修5》的阅读与思考“海伦和秦九韶”的基础上进行创新,设置优秀传统文化情境，体现了高考试题的创新性原则.

A.6平方米 B.9平方米

C.12平方米 D.15平方米

【参考答案】B

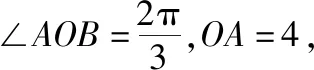
【变式说明】《九章算术》是我国较早的一部流传至今的著名数学专著.《九章算术》内容丰富，而且大多和实际生活密切联系，这些密切联系实际生活的题材，反映出我国古代先贤的智慧，同时也显示出古代中国数学的研究多以实用性为主.本题以《九章算术》中“算弧田面积所用的经验方式”为背景，与高考中的图形相匹配，让学生领略中华民族的智慧和数学研究成果，进一步树立民族自信心和自豪感，培育爱国主义情感.

【参考答案】A

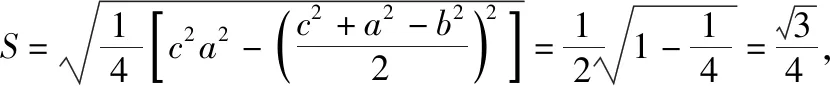
【变式说明】在《普通高中课程标准实验教科书A版必修5》的阅读与思考“海伦和秦九韶”的基础上进行创新,首先给出一段阅读材料，然后利用题中所给公式，运用正弦定理和整体思想求解，旨在弘扬中华优秀传统文化，让学生感受中国的传统文化之美并予以传承.

【参考答案】C

【变式说明】在《普通高中课程标准实验教科书A版必修5》的阅读与思考“海伦和秦九韶”的基础上进行创新，在已知三角形面积的前提下，逆用秦九韶公式求边长，以此引导学生理解数学，感受探究、解决数学问题的过程，进而体会中国古代数学的伟大贡献，增强爱国主义情怀.

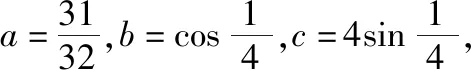
A．c>b>aB．b>a>c

C．a>b>cD．a>c>b

【参考答案】A

【创新点说明】本题是2022年全国甲卷第12题，主要考查三角函数大小的比较；考查了学生运用所学知识分析、转化、解决问题的能力，同时也考查了学生的观察能力与运算能力，体现了高考的全面性、基础性和综合性原则；比较大小问题在选择压轴题出现过若干次，与以往不同的是，之前大多是以指数和对数为背景的比较大小，而今年则是以三角函数为背景的比较大小，体现了高考的创新性原则.

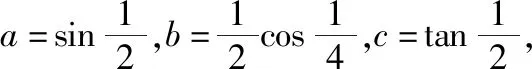
A．c>b>aB．b>c>a

C．c>a>bD．a>b>c

【参考答案】A

【解题思路】方法一(作商法)：

观察答案A和B,我们需要比较b和c的大小，

故选A.

方法二(作差法)：

所以a

观察答案A和B,我们需要比较b和c的大小，

方法三(构造函数法)：

a和b的大小比较同上，这里就不赘述了，我们这里着重比较b和c的大小，

f′(x)=cosx-cos2x+2xsin2x=-2cos2x+cosx+1+2xsin2x,

所以有c-b>0，即c>b，故选A.

方法四(泰勒公式)：

新人教版A版教材必修一第256页习题第26题是这样的：

英国数学家泰勒发现了如下公式：

其中n!=1×2×3×4×…×n.

试用你的计算工具计算cos0.3，并与上述结果比较.

根据上述的描述，我们也用前三项来计算，可得

比较可得答案，故选A.