例析三道四点共面问题

广东 龙 宇 黄玉平

而我们在解题或命题的过程中，常常忽略掉四点共面这一要求，从而导致求解失误.接下来本文以三道易错的四点共面问题为例，分析其错解的根源.

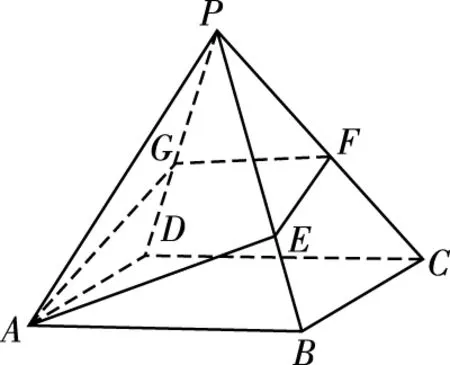
图1

【错解】如图2，将四棱锥P-ABCD的侧面展开成平面，连接AA′，则AA′的值即为截面四边形AEFG周长的最小值.计算过程如下：

因为P-ABCD为正四棱锥，故可得∠APB=∠BPC=∠CPD=∠DPA′，设∠APB=θ.

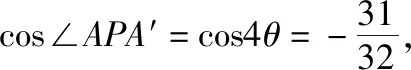
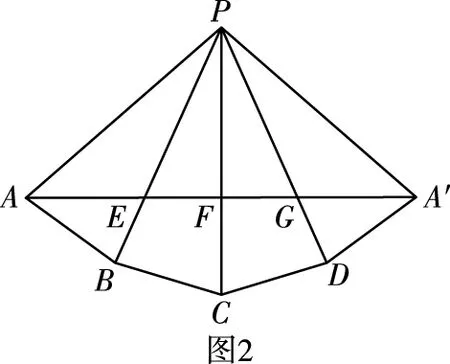
【错解辨析】本题的解题关键在于将四边形AEFG的周长转化为平面图形中两点间的距离，解题错误在于将四棱锥P-ABCD展开时，四边形AEFG的各边能否形成一条直线.等价于在图2中，若将展开图还原为正四棱锥P-ABCD时，由线段AA′形成的四边形AEFG是否在同一个平面内呢？答案是否定的，由此可知上述解答过程是错误的.

其理由如下：假设在图2的条件下，图1中的四边形AEFG在同一个平面内.在图2中易知PF⊥EF，PF⊥GF，由此可知在图1中PC⊥平面AEFG.

由题可知△PAC为等边三角形，由此可得PF=1(即F为PC的中点)，设AC与BD的交点为O，连接PO，设PO与AF的交点为M，易知M为△PAC的重心，从而可得PM∶MO=2∶1.

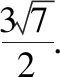
【试题2】如图3，在棱长为6的正方体ABCD-A1B1C1D1中，点E，F分别在C1D1与C1B1上，且C1E=4，C1F=3，求几何体EFC1-DBC的体积.

【分析】因为延长BF，DE与CC1的交点不是同一个点，即可得几何体不是台体.为此需通过割补的思想来进行求解.

【解法一】如图4-1，连接DF，DC1，则几何体EFC1-DBC被分割成三棱锥D-EFC1及四棱锥D-CBFC1，则可得VEFC1-DBC=VD-EFC1+VD-CBFC1=66.

【解法二】如图4-2，连接BE，BC1，则几何体EFC1-DBC被分割成三棱锥B-EFC1及四棱锥B-CDEC1，则可得VEFC1-DBC=VB-EFC1+VB-CDEC1=72.

【错解辨析】为什么两种解法的结论不同呢？其根源在于点E，F，B，D不在同一个平面内，四边形EFBD为空间四边形.通过不同的割补方法使得空间四边形EFBD在几何体EFC1-DBC中出现的部分不同，导致计算的结果有差异.

在2019年人教A版必修二教材中对于多面体的定义为：一般地，由若干个平面多边形围成的几何体叫做多面体.在本题中，几何体EFC1-DBC由四个平面多边形和一个空间四边形构成，不符合多面体的概念.按照高中的定义，该几何体所指的图形意义不明确，题干出现了歧义.

为了保证几何体EFC1-DBC为体积可计算的几何体，需使得点E，F，B，D四点共面.在正方体中，平面A1B1C1D1//平面ABCD，点E，F，B，D四点共面等价于EF//BD，即需满足C1E=C1F，方可计算几何体EFC1-DBC的体积，此时该几何体为棱台，利用相关公式计算即可.

【问题修正】如图3，在棱长为6的正方体ABCD-A1B1C1D1中，点E，F分别在C1D1与C1B1上，且C1E=C1F=4，求几何体EFC1-DBC的体积.

【答案】此时即可利用棱台的公式求解，答案为76.

【试题3】图5为四棱锥A-DEFG的侧面展开图(点G1，G2重合为点G)，其中AD=AF，G1D=G2F，E是线段DF的中点，请写出四棱锥A-DEFG中一对一定相互垂直的异面直线：________.

【分析】在本题中，因为AD=AF，E是线段DF的中点，根据等腰三角形的性质可得AE⊥DF，所以将图5还原成四棱锥A-DEFG时，可得AE⊥平面DGFE，结合G1D=G2F可得四边形DGFE为“筝形”.其图形如图6，符合题干条件的答案就包括：AE与GF，AE与GD.本题考查线面垂直的性质定理，以及翻折图形在变化过程中的不变性，思维的难度并不大.但在求解的过程中，学生提出如下质疑，在图5的条件下，其能否围成一个四棱锥呢？等价于点D，E，F，G四点是否在一个平面内呢？

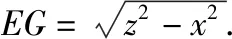
设∠AFG=θ，∠EFG=α，在△AFG中利用余弦定理可得，z2=AF2+FG2-2AF·FGcosθ；

在△EFG中利用余弦定理可得EG2=EF2+FG2-2EF·FGcosα；