一道2022年高考三角试题的思考
2022-11-19安徽杨光明
安徽 杨光明
本文就2022年高考数学全国乙卷的三角试题从学生视角分析,通过对学生的错误剖析为教师教学提供一点建议.
章建跃博士在他的著作《数学教育随想录》中阐述过从数学角度衡量,“好题”应具有以下“品质”:与重要的数学概念和性质相关,体现基础知识的联系性,解题方法自然、多样,表述形式简洁、流畅、好懂等.如果以这个为标准,2022年高考数学全国乙卷理科的第17题可以说是道好题.
1.题文解析
【例题】(2022·全国乙卷理·17)记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A-B)=sinBsin(C-A).
(1)证明:2a2=b2+c2;
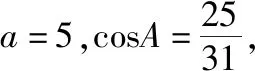
本题是一道解三角形问题,第(1)问的难度要大于第(2)问.面对这道好题,笔者自然不会“浪费”,从而得到本题的如下解法:
第(1)问解法一:由题干条件利用两角差的正弦公式展开化简有
sinC(sinAcosB-cosAsinB)=sinB(sinCcosA-cosCsinA), ①
整理得,
sinAcosBsinC+sinAsinBcosC=2cosAsinBsinC,
等式左边提取公因式sinA,再利用两角和的正弦公式整理得
(sinA)2=2cosAsinBsinC, ②
再利用正弦定理和余弦定理化简
最后整理得证2a2=b2+c2.
第(2)问解法一:由第(1)问及a=5得,b2+c2=50,
③
得2bc=31, ④
故(b+c)2=b2+c2+2bc=81⟹b+c=9,故有△ABC的周长为a+b+c=14.
2.学生视角
为了了解学生的想法笔者让高二学生提前感受了一下高考.下面整理几种学生常见的解法:
学生1:同解法一得到①式后直接利用正弦定理把角化边得
accosB-bccosA=bccosA-abcosC,
再代入化简得证2a2=b2+c2.
与解法一比较而言,学生1的思路更加自然,证明思路更加清晰明确.
学生2:由题干条件利用三角形内角和及诱导公式化简得,
sin(A+B)sin(A-B)=sin(C+A)sin(C-A), ⑤⟹
(a+b)(a-b)=(c+a)(c-a), ⑥
展开化简得证2a2=b2+c2.
笔者在和学生交流时,其他同学都惊讶于学生2的思路简洁,但遗憾的是⑥式错了,而不少同学没有发现错误.
学生3:与学生2一样得到⑤式再利用两角和与差的正弦公式代入有
sin2Acos2B-cos2Asin2B=sin2Ccos2A-cos2Csin2A,
又sin2α+cos2α=1,
故有sin2A(1-sin2B)-(1-sin2A)sin2B=sin2C(1-sin2A)-(1-sin2C)sin2A,
再利用正弦定理角化边得,
a2(1-b2)-(1-a2)b2=c2(1-a2)-(1-c2)a2, ⑦
整理得证2a2=b2+c2.
笔者在和学生交流时,其他同学都认为学生3延续学生2的思路解决了问题,但⑦式错了,这里只有更少的同学发现错误.
学生4:第(1)问解法二:与学生2一样得到⑤式,再利用两角和与差的正弦公式代入有
sin2Acos2B-cos2Asin2B=sin2Ccos2A-cos2Csin2A,
又sin2α+cos2α=1,
故有sin2A(1-sin2B)-(1-sin2A)sin2B=sin2C(1-sin2A)-(1-sin2C)sin2A,
整理得sin2A-sin2B=sin2C-sin2A,
再利用正弦定理角化边得a2-b2=c2-a2,
整理得证2a2=b2+c2.
学生4吸取前两位同学的“前车之鉴”,最终解决了问题.
学生5想要把条件sinCsin(A-B)=sinBsin(C-A)中三个角统一为两个角,但试了一下发现很困难,于是就放弃了.笔者认为这个想法从化简的角度可行,于是也做了尝试:
第(1)问解法三:利用三角形内角和定理得,
sinCsin(π-2B-C)=sinBsin(2C+B-π),
利用诱导公式化简得,
sinCsin(2B+C)=-sinBsin(2C+B),
利用两角和的正弦公式得,
sinC[sin(B+C)cosB+cos(B+C)sinB]=-sinB·[sin(B+C)cosC+cos(B+C)sinC],
展开化简整理有
sin2(B+C)=-2cos(B+C)sinBsinC⟹sin2A=
2cosAsinBsinC,
下面化简同解法一.
学生6换了一个角度提出了自己的想法,第(1)问解法四(分析法):
要证2a2=b2+c2,又由余弦定理,
a2=b2+c2-2bccosA,
只要证a2=2bccosA,
再由正弦定理只要证(sinA)2=2cosAsinBsinC,
只要证
sinAcosBsinC+sinAsinBcosC=2cosAsinBsinC,
只要证sinC(sinAcosB-cosAsinB)=sinB(sinCcosA-cosCsinA),
只要证sinCsin(A-B)=sinBsin(C-A).
而sinCsin(A-B)=sinBsin(C-A),题意已知,故证毕.
对于第(2)问,有学生选择联立③式与④式想要求出边b或c,但算不出来所以选择放弃,笔者也进行了尝试,得到了如下解法:
第(2)问解法二:同解法一得到b2+c2=50, ③与2bc=31, ④
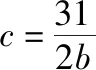
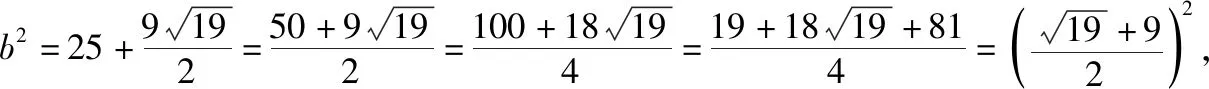
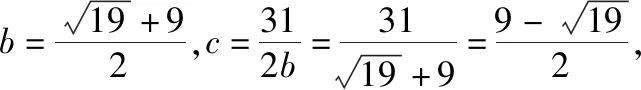
故有△ABC的周长为a+b+c=14.
很明显,如果想要联立方程求出b或c的话会出现⑧式,计算量会很大,但是在求圆锥曲线的离心率问题时也常出现根式的化简问题,故也要落实数学运算核心素养.
3.错误与剖析
安徽省首批正高级教师陆学政教授曾经说过:“只有在最需要学生利用核心素养解决问题时才能真正地提升学生的核心素养.”学生犯错误正是提升学生核心素养的时机,于是笔者开始思考以下两个问题:
问题一:学生2的思路能否解决本题呢?
问题二:如何向学生解释⑥式以及⑦式错了,学生能主动地接受,而不是被动地“承认”?
针对问题一学生4已经提出了自己的想法,关于⑤式的利用,笔者也继续给出了其他做法:
第(1)问解法五:与学生2一样得到⑤式,由两角和与差的余弦公式:
cos(α+β)=cosαcosβ-sinαsinβ与cos(α-β)=cosαcosβ+sinαsinβ,
后式减前式化简得,
故⑤式化简有
整理得,cos(2B)+cos(2C)=2cos(2A),
由余弦的二倍角公式化简有sin2B+sin2C=2sin2A,
再利用正弦定理得证2a2=b2+c2.
问题二:如何向学生解释⑥式以及⑦式错了,学生能主动的接受,而不是被动的“承认”?
在利用正弦定理实现边角互化时,学生甚至为了寻求“方便”,经常直接将角换成边或者将边换成角,并且还很难发现错误.教师会直接指出学生错误,这种做法固然没有问题,但学生往往会“承认错误”,然后“屡屡再犯”.如何让学生主动的“接受”而“引以为戒”呢?罗增儒教授很早就给出了答案:要通过反例或启发等途径暴露矛盾,引导当事者自我反省.直接告知正确答案的做法未必能达到预期的效果,毕竟学生不是一张可以任意涂上各种颜色的白纸,不是一个空的、可以直接塞进各种真理的容器.作为对错解的对比、补救或纠正,给出正确解法是绝对有必要的.但笔者建议,尽可能直接在原解法的基础上进行完善(然后再另外提供优秀解法),使学生体会并学会“怎样改正错误”.因此笔者做了简单的尝试,在和学生交流时设计了如下“陷阱”:

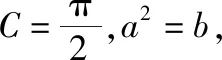
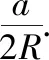
最后关于本题笔者还给学生留了两个思考,也和同行们分享:
1.sin(A-B)与a-b有没有关系?
2.能否利用几何角度解决本题?

