“函数与导数”专题易错分析与练习

新疆 师 斌

【易错点名称】函数零点问题应用不清致误

(1)当a=0时，求f(x)的最大值；

(2)若f(x)恰有一个零点，求a的取值范围．

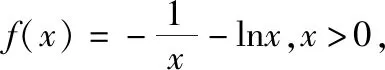
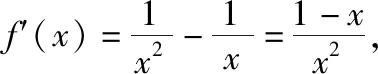
当x∈(0,1)时，f′(x)>0，f(x)在(0，1)上单调递增；当x∈(1,+∞)时，f′(x)<0，f(x)在(1，+∞)上单调递减；所以f(x)max=f(1)=-1.

(易错：忽视对参数a的分类讨论，应用零点存在性定理时，数形结合不充分、不恰当)

当a≤0时，ax-1<0，所以当x∈(0,1)时，f′(x)>0，f(x)在(0，1)上单调递增；

当x∈(1,+∞)时，f′(x)<0，f(x)在(1，+∞)上单调递减；

所以f(x)max=f(1)=a-1<0，此时函数无零点，不符合题意；

(易错：忽视当x趋近正无穷大时函数值符号的判断)

所以f(x)在(0，+∞)上单调递增，

又f(1)=a-1=0，所以f(x)有唯一零点，符合题意；

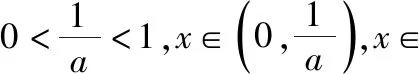
(易错：忽视当x趋近零时函数值符号的判断)

综上，a的取值范围是(0,+∞).

【易错分析】在解决含参数的函数零点问题时，通常需要转化为图象问题，而化归与转化、数形结合、分类与讨论思想对学生的能力要求较高，容易失误.

【易错数据】本次共统计了39名学生的易错数据，其中有5名优良分数段的学生做错，15名及格分数段的学生做错，16名不及格分数线的学生做错，只有3名学生做对，可以发现该题普遍得分率不高，错误的人数较多，几乎全军覆没，属于典型易错题.

【答案】C

【解题思路】当x≤0时，f(x)=x+3x在(-∞,0]上单调递增，

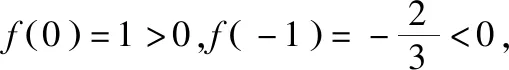
所以f(x)在(-∞,0]内存在唯一零点;

(易错：当x≤0时，利用作图或零点存在性定理得出零点个数的基本功不扎实)

f′(x)=x2-4，令f′(x)>0，则x>2或x<-2(舍去),

所以f(x)在(0,2]上单调递减，在(2,+∞)上单调递增，

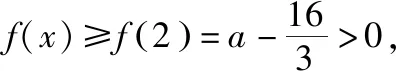
(易错：当x>0时，数形结合不到位，没有把问题简化为极小值f(2)>0．)

故选C．

【答案】D

(易错：把函数零点问题转化为两函数图象交点个数问题时，没有变形出一次函数，增加了难度)

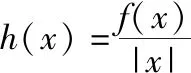
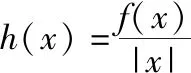
由式(4)第1式、式(11)、式(12)、以及图1的△OA1B1、△OA2B2知，当φ为φ1、φ2时，φ为0、180，δ为δmax、δmin，α为α1、α2，注意到式(13)即知φ1、φ2是αmax可能出现位置。

当k>0时，如图，当y=kx-2与y=x2相切时，联立方程得x2-kx+2=0，

(易错：数形结合与分类讨论时遗漏情况)

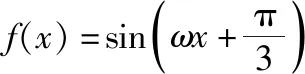
【答案】C

【解题思路】依题意可得ω>0，

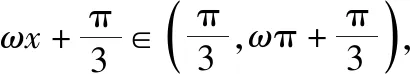
要使函数在区间(0,π)上恰有三个极值点、两个零点，

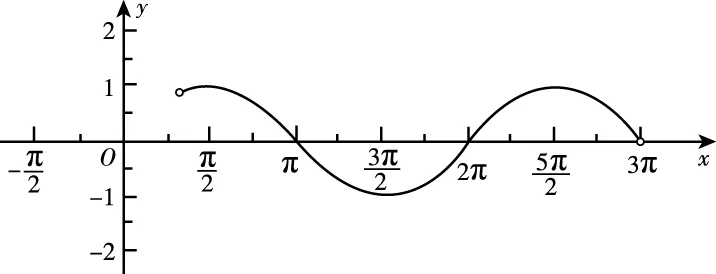
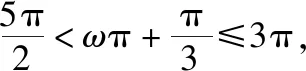
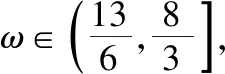
(易错：没有熟练掌握三角函数图象特征)

【答案】3

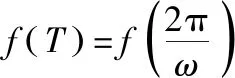
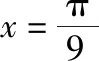
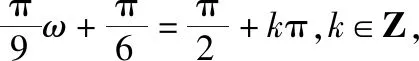
解得ω=3+9k,k∈Z，

因为ω>0，所以当k=0时ωmin=3,故答案为3.

(易错：没有列出满足零点的等式并变形出ω的表达式)

5．(2022·江西师大附中三模)定义在R上的函数f(x)满足f(-x)+f(x)=0,f(x)=f(2-x)，且当x∈[0,1]时，f(x)=x2,则函数y=7f(x)-x+2的所有零点之和为( )

A．7 B．14 C．21 D．28

【答案】B

【解题思路】依题意，f(x)是奇函数.

又由f(x)=f(2-x)知，f(x)的图象关于x=1对称.

f(x+4)=f(1+(x+3))=f(1-(x+3))=f(-2-x)=-f(2+x)=-f(2-(-x))=-f(-x)=f(x)，

所以f(x)是周期为4的周期函数.

f(2+x)=f(1+(1+x))=f(1-(1+x))=f(-x)=-f(x)=-f(2-x)，

所以f(x)关于点(2,0)对称.

(易错：不会分析函数的周期性和对称性)

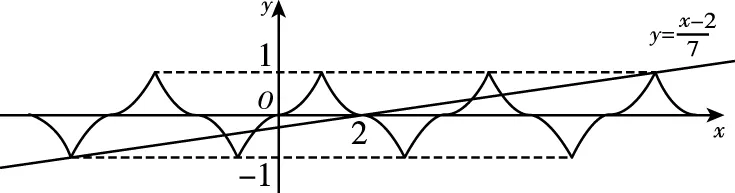
(易错：零点之和与图象、对称性没有很好地结合，导致失误)

6．(2022·江苏二模)设函数f(x)=aex+sinx-3x-2，e为自然对数的底数，a∈R.

(1)若a≤0，证明：函数f(x)有唯一的零点；

(2)若函数f(x)有唯一的零点，求a的取值范围.

【解题思路】

(1)证明：当a≤0时，f′(x)=aex+cosx-3<0恒成立，所以f(x)在(-∞，+∞)上单调递减，

又f(0)=a-2<0，

(易错：零点所在区间找端点不恰当)

(2)由(1)可知，当a≤0时，f(x)有唯一零点，

(易错：构造函数不恰当)

设h(x)=cosx-sinx+3x-1，

则h′(x)=-cosx-sinx+3>0，

所以h(x)在(-∞，+∞)上单调递增，

又h(0)=0，可知，g(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增，

即g(x)min=g(0)=a-2，

当a>2时，g(x)>0恒成立，无零点，即a>2不符题意，

当a=2时，g(x)min=g(0)=0，即g(x)仅有一个零点x=0，即a=2符合题意，

当0

因为g(-1)=(1-sin1)e+a>0，即f(-1)>0,

(易错：分类讨论、数形结合遗漏情况；零点所在区间找端点不恰当)