交换环上的w*-模
2022-11-18陶蕴芝王芳贵李建鸿
陶蕴芝,王芳贵,李建鸿
(四川师范大学数学科学学院,四川 成都 610066)
1997年王芳贵和R.L.Mclaslan[1]引入了整环上的w-模的概念,使得整环上的星型算子理论在模范畴发挥了重要作用。自然地,人们希望这样的做法能用于一般交换环上。2011年,尹华玉等人[2]用Hom与Ext函子把整环上的w-模理论推广到了一般交换环上,这使得w-模理论更能适用于一般交换环中,因而受到了众多学者们的广泛关注与研究。众多学者们用交换环上的w-模理论对一些经典环模类概念进行推广刻画,例如w-Noether环w-凝聚环等。在许多情形,人们通常以R的完全商环T(R)(设S是R的所有非零因子构成的乘法封闭集,记T(R)=RS,称之为R的完全商环)的行为来代替整环时商域的行为,用正则理想代替整环的非零理想。本文尝试考虑只用正则w-理想来刻画环的结构性质。为此,我们提出了w*-模的概念,定义了模的w*-包络,建立交换环上w*-模理论。进而给出w-Noether环和SM环的一些新的刻画。
Noether环是指每个理想是有限生成的环,学者们在文献[3-10]中都有对Noether环进行研究推广,它是应用很广泛的环类,有许多经典的结论,其中一个著名的结论就是Cartan-Eilenberg-Bass定理[3],即R是Noether环,当且仅当任意多个内射模的直和是内射模。该结论由于其重要性得到了许多推广,例如,2002年Beider等[9]证明了局部Noether环形式的Cartan-Eilenberg-Bass定理。2008年Kim等[11]得到了SM整环上的Cartan-Eilenberg-Bass定理,即整环R是SM整环,当且仅当任意多个GV-无挠的内射模的直和是内射模。2010年,王芳贵等人[12]得到了更一般的w-Noether环上的w-版本的Cartan-Eilenberg-Bass定理。2011年,王芳贵等人[13]将SM整环的讨论推广到了一般交换环上,引入了SM环的概念,即满足正则w-理想的升链条件的环。并利用GV-无挠模与正则性内射模建立了SM环上的Cartan-Eilenberg-Bass定理。本文也将给出另一形式的Cartan-Eilenberg-Bass定理,证明了R是SM环当且仅当任意多个GV*-无挠的正则性内射模的直和是正则性内射模。
本文恒设R是单位元为1的交换环。对R-模M,用E(M)表示M的内射包络,e(M)表示M的正则性内射包络。设I是R的理想,若I中包含R的一个非零因子,则I称为正则理想。若存在I的有限生成子理想I0,使ann(I0)=0,则I称为R的半正则理想。显然正则理想是半正则的。环R的GV-理想都是半正则的,但未必是正则的。
1 预备知识
引理1.1[14]设A∈GV(R[X]),则A中包含R[X]中的一个非零因子.
命题1.2[15]设R是环,则
(1)R∈GV(R)。
(2) 设J1,J2是R的理想,且J1⊆J2。若HomR(J1,R)≅R,则HomR(J2,R)≅R。即若J1∈GV(R),且J2为有限生成时,则J2∈GV(R)。
(3) 若J1,J2∈GV(R),则J1J2∈GV(R)。
定理1.3[15]设M是有限表现R-模,{Ci}是一簇模。则

(2) 设R是凝聚环,则对任何n≥1,有
(3) 设R是凝聚环,则对任何n≥1,有
命题1.4[13]E是R-模,则以下各条等价:
(1)E是S-内射模。
(2) 对任何R-正合列0→A→B→C→0,只要C∈S,则
0→HomR(C,E)→HomR(B,E)→HomR(A,E)→0
也是正合列。
(3) 对任何模的扩张A⊆B,只要B/A∈S,则任何同态f:A→E可以扩张到B。
(4) 对任何R-正合列0→E→B→C→0,只要C∈S,则该正合列是分裂的。
推论1.5[12]设R是w-Noether环,I是R的理想,且ann(I)=0,则I中包含R的非零因子。特别地,若J∈GV(R),则J中包含R的非零因子。
定理1.6[12]对环R,以下各条等价:
(1)R是w-Noether环。
(2) 任意多个GV-无挠的内射模的直和是内射模。
(3) 可数无限个GV-无挠的内射模的直和是内射模。
(4) 每个GV-无挠的内射模是Σ-内射模。
定理1.7[16](1) 设M是有限表现模,则
(2)δ是单同态,且当M是有限生成模时,δ是同构。即
⊕HomR(M,Ai)≅HomR(M,⊕Ai)。
定理1.8[13]对环R,以下各条等价:
(1)R是SM环。
(2) 任意多个GV-无挠的正则性内射模的直和是正则性内射模。
(3) 可数无限个GV-无挠的正则性内射模的直和是正则性内射模。
(4) 每个GV-无挠的正则性内射模是Σ-正则性内射模。
2 GV*-理想
设R是交换环,J是R的有限生成理想,如果自然同态φ:R→J*=HomR(J,R)是同构,则J称为R的GV-理想。用GV(R)表示R的GV-理想的集合。以下用GV*(R)表示R的正则GV-理想的集合,GV*(R)中的元素称为GV*-理想。
当R是整环时,则R的非零理想都是正则理想,因此有R的GV-理想是GV*-理想,即GV*(R)=GV(R)。
回顾环R称为DW环,是指R的每个理想都是w-理想,等价地,GV(R)={R}。在文献[15]称环R为弱DW环,是指R的每个正则理想都是w-理想,等价地,GV*(R)={R}。显然,若T(R)=R,则R是弱DW环。
尽管有GV*(R)⊆GV(R),但反包含关系未必成立。
例2.1取文献[17]给出的环R,满足T(R)=R,且R不是DW环。故此时有GV*(R)={R},则GV(R)GV*(R)。
命题2.2对任何环R,R[X]是多项式环,则GV*(R[X])=GV(R[X])。
证明由引理1.1,R[X]的半正则理想都是正则理想,因此有GV*(R[X])=GV(R[X])。
设S是R的理想的集合,若S满足:(1)R∈S;(2)若I,J∈S,则IJ∈S,则称S是R的理想的乘法系。
命题2.3(1)R∈GV*(R)。
(2) 若J1,J2∈GV*(R),则J1J2∈GV*(R)。
(3) 设J1,J2是R的理想,且J1⊆J2。若J1∈GV*(R),且J2为有限生成正则时,则J2∈GV*(R)。
证明(1) 显然。
(2) 我们知道R的GV-理想和R的有限生成正则理想的集合都是R的理想的乘法系,由条件J1,J2∈GV*(R)⊆GV(R),故J1J2∈GV(R)。又J1,J2为有限生成正则理想,故J1J2也为有限生成正则理想,因此有J1J2∈GV*(R)。
(3) 由于J1是正则理想,故有J2是正则理想。由命题1.2,J2∈GV(R),因此有J2∈GV*(R)。
定义2.4设M是R-模,令
torGV*(M)={x∈M|存在J∈GV*(R),
使得Jx=0}
由于GV*(R)是R的理想的乘法系,则有torGV*(M)是M的子模,称之为M的完全GV*-挠子模。若torGV*(M)=M,则称M为GV*-挠模。若torGV*(M)=0,则称M为GV*-无挠模。
由定义可立即得到:
命题2.5设M是R-模,则有
(1)M是GV*-挠模当且仅当对任何x∈M,存在J∈GV*(R),使得Jx=0。
(2)M是GV*-无挠模当且仅当由J∈GV*(R),x∈M和Jx=0,能推出x=0。
注2.6以下的事实是显然的:
(1) GV*-挠模的子模与商模还是GV*-挠模,GV*-无挠模的子模还是GV*-无挠模。
(2) 对给定的模M,令T=torGV*(M),则T总是GV*-挠模,M/T总是GV*-无挠模。
(3) GV-无挠模是GV*-无挠模,GV*-挠模是GV-挠模。从而有投射模,平坦模与自反模都是GV*-无挠模。
(4) 若M既是GV*-挠模,又是GV*-无挠模,则M=0。
(5) 设J∈GV*(R),则R/J是GV*-挠模。
例2.7设J∈GV(R),但JGV*(R),则M:=R/J是GV-挠模,但M不是GV*-挠模,故GV-挠模未必是GV*-挠模。
我们可以对GV*-无挠模作一些函子性质刻画。
命题2.8设M是R-模,则以下各条件等价:
(1)M是GV*-无挠模。
(2)J∈GV*(R),则HomR(R/J,M)=0。
(3) 对任何J∈GV*(R),自然同态φ:M→HomR(J,M)是单同态。
(4) 对任何J∈GV*(R),及任何R/J-模B,HomR(B,M)=0。


(2)⟺(3) 由正合列
即得。
(2)⟹(4) 设F=⊕R/J是自由R/J-模,f:F→B是满同态,则有正合列:
0→HomR(B,M)→HomR(F,M)≅∏HomR(R/J,M),
故HomR(B,M)=0。
(4)⟹(2) 取B=R/J即得,其中J取遍R的GV*-理想。
命题2.9(1)M是GV*-挠模当且仅当对任何GV*-无挠模N,HomR(M,N)=0。
(2)N是GV*-无挠模当且仅当对任何GV*-挠模M,HomR(M,N)=0。
证明(1) 设M是GV*-挠模,N是GV*-无挠模,f∈HomR(M,N)。若x∈M,有J∈GV*(R),使得Jx=0。因此,Jf(x)=0。由于N是GV*-无挠模,故f(x)=0。于是有f=0,即有HomR(M,N)=0。
反之,设T=torGV*(M),N=M/T。于是N是GV*-无挠模。由于HomR(M,N)=0,则自然同态π:M→N是零同态。因此有N=0,即M=T是GV*-挠模。
(2) 设N是GV*-无挠模。由(1)知对任何GV*-挠模M,HomR(M,N)=0。
反之,设M=torGV*(N),则有HomR(M,N)=0。故包含同态M→N是零同态。因此有M=0,故N是GV*-无挠模。
命题2.10(1) 设{Mi}是一簇R-模,则∏Mi是GV*-无挠模当且仅当每个Mi是GV*-无挠模。
(2) 若M是GV*-无挠模,E(M)也是GV*-无挠模。
(3) 设M是任何R-模,N是GV*-无挠模,则HomR(M,N)是GV*-无挠模。
证明(1) 对任意J∈GV*(R),由自然同构HomR(R/J,∏Mi)≅∏HomR(R/J,Mi)即得。
(2) 设x∈E(M),J∈GV*(R),Jx=0。若x≠0,由于E(M)是M的本性扩张,故存在r∈R使得rx≠0且rx∈M。于是有Jrx=0。由于M是GV*-无挠模,得到rx=0,矛盾。故x=0,因此E(M)是GV*-无挠模。
(3) 设f∈HomR(M,N),J∈GV*(R),Jx=0。则对任意x∈M,Jf(x)=0。由于N是GV*-无挠模,故f(x)=0。因此f=0。故HomR(M,N)是GV*-无挠模。
设M是R-模,S是由R的全部非零因子构成的乘法封闭集。若MS=0,等价地,对任何x∈M,存在s∈S,使得sx=0,则M称为挠模。若由sx=0,其中s∈S,x∈M,能推出x=0,则M称为无挠模。
命题2.11(1) 设M是无挠模,则M是GV*-无挠模。
(2) 设M是GV*-挠模,则M是挠模。
证明(1) 设J∈GV*(R),x∈M,Jx=0。因J中含有非零因子,设为s,则sx=0。因M是无挠模,可得x=0,故M是GV*-无挠模。
(2) 设x∈M,则存在J∈GV*(R),使得Jx=0。由于J是正则理想,则有非零因子s∈J,使得sx=0。故M是挠模。
推论2.12设M是T(R)-模,则M作为R-模是GV*-无挠模。
证明由M作为R-模是无挠模和引用命题2.11即得。

证明对任何J∈GV*(R),由于R/J是有限表现模,则
HomR(R/J,F⊗RM)≅F⊗RHomR(R/J,Mi)=0
因此,由命题2.8,F⊗RM是GV*-无挠模。
推论2.14(1) 设N是GV*-无挠模,则对R的任何乘法集S,NS作为R-模是GV*-无挠模。
(2)T(R)是GV*-无挠模。
证明(1) 由NS=RS⊗RN并引用命题2.13即得。
(1)由(1)即得。
3 w*-模


推论3.2GV*-无挠的正则性内射模是w*-模。
证明由正则性内射模的定义与定义3.1即得。
命题3.3(1) 设M是GV*-无挠模,则E(M)和e(M)是w*-模。
(2) 设{Mi}是一簇R-模,则∏Mi是w*-模当且仅当每个Mi是w*-模;当且仅当⊕Mi是w*-模。
证明(1) 由命题2.10知E(M)是GV*-无挠模,从而有e(M)也是GV*-无挠模。因此得到E(M)和e(M)是w*-模。
(2) 对任意J∈GV*(R),由自然同构
得到∏Mi是w*-模当且仅当每个Mi是w*-模。
以及由定理1.3,
得到⊕Mi是w*-模当且仅当每个Mi是w*-模。
注3.4(1) 由于GV-无挠模是GV*-无挠模,故每个w-模是w*-模。因此,投射模,平坦模,对偶模与自反模都是w*-模。当R是整环时,每一w*-模也是w-模。
(2) 若R是弱DW环,则任意R-模都是w*-模。故若R是弱DW环,但不是DW环,则一定有一个R-模不是w-模。因此,未必有每个w*-模是w-模。
定理3.5设M是GV*-无挠模,则以下各条等价:
(1)M是w*-模。
(2) 对任何J∈GV*(R),任何同态f:J→M可以扩张到R上。
(3) 对任何J∈GV*(R),自然同态φ:M→HomR(J,M)是同构。

证明(1)⟺(2)设J∈GV*(R),考虑正合列
0→HomR(R/J,M)→HomR(R,M)→
(3.1)

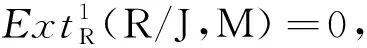
(1)⟹(4)设F=⊕R/J是自由R/J-模,f:F→B是满同态.记L=Ker(f),则有正合列

(4)⟹(1)取B=R/J即得,其中J取遍R的GV*-理想。
命题3.6设M是GV*-无挠模,则以下各条等价:
(1)M是w*-模。
(2) 对任何正合列0→M→N→C→0,只要N是w*-模,就有C是GV*-无挠模。
(3) 存在一个正合列0→M→N→C→0,使得N是w*-模,C是GV*-无挠模。
证明(1)⟹(2)设J∈GV*(R)。考虑正合列
HomR(R/J,N)→HomR(R/J,C)→

(2)⟹(3)取N=E(M)即知。
(3)⟹(1)设J∈GV*(R)。考虑正合列

定理3.7设N是w*-模,M是N的子模,则M是w*-模当且仅当由Jx⊆M,x∈N和J∈GV*(R)能推出x∈M。
证明考虑正合列
0→M→N→N/M→0。

反之,由条件N/M是GV*-无挠模,仍由定理3.6得M是w*-模。
文[2]指出,GV-无挠模M是w-模当且仅当由Jx⊆M,其中J∈GV(R),x∈E(M),能推出x∈M。同样能够得到:
定理3.8设M是GV*-无挠模,则以下各条等价:
(1)M是w*-模。
(2)由Jx⊆M,其中J∈GV*(R),x∈E(M),能推出x∈M。
(3) 由Jx⊆M,其中J∈GV*(R),x∈e(M),能推出x∈M。
证明(1)⟹(2)由定理3.7与命题3.3即得。
(2)⟹(1)设J∈GV*(R),f:J→M。由于E(M)是内射模,故存在同态g:R→E(M)使得下图可交换:
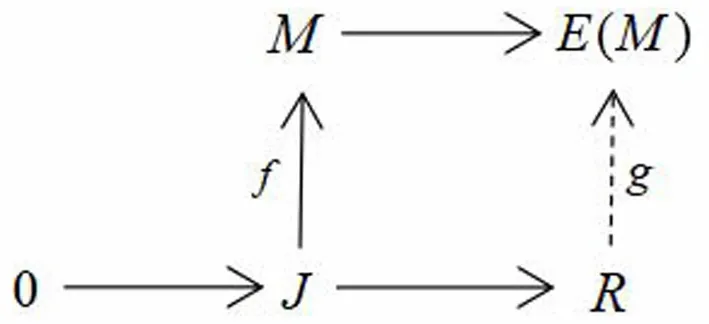
记g(1)=x∈E(M),则g(J)=Jx=f(J)⊆M。由条件x∈M,故Im(g)⊆M,即g:R→M是f的扩张,由定理3.5有M是w*-模。
(1)⟺(3)完全类似于(1)⟺(2)的证明。
定理3.9设M是任何R-模,N是w*-模,则HomR(M,N)是w*-模。
证明设0→A→F→M→0是正合列,其中F=⊕R是自由模,于是有正合列
0→HomR(M,N)→HomR(F,N)→
HomR(A,N),
由命题3.3
HomR(F,N)=HomR(⊕R,N)≅∏N
是w*-模,由命题2.10,HomR(A,N)是GV*-无挠模。故由定理3.6,HomR(M,N)是w*-模。
命题3.10设0→A→B→C→0是正合列,且A和C都是w*-模,则B也是w*-模。
证明设J∈GV*(R),则有正合列
HomR(R/J,A)→HomR(R/J,B)→
HomR(R/J,C),
和正合列
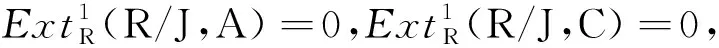

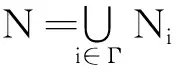
证明设J∈GV*(R),x∈M,Jx⊆N。由于J是有限生成的,故存在指标i,使得Jx⊆Ni。由定理3.7,x∈Ni。由此可得N是w*-模。
命题3.12设M是GV*-无挠模,x∈M,则ann(x)是R的w*-理想。
证明设J∈GV*(R),a∈R,使得Ja∈ann(x)。则Jax=0。由于M是GV*-无挠模,故ax=0。因此有a∈ann(x),故ann(x)是w*-理想。
命题3.13设M是w*-模,N是GV*-无挠模,f:M→N是同态,则Ker(f)是M的w*-子模。
证明考虑正合列
0→Ker(f)→M→Im(f)→0,
因N是GV*-无挠模,故Im(f)也是GV*-无挠模。由定理3.6,Ker(f)是w*-模。
命题3.14设S是R的乘法集,M是S-无挠的w*-模,则MS作为R-模是w*-模。
证明由推论2.14,MS是GV*-无挠模。故E(MS)是w*-模。设
J=(a1,a2,…,an)∈GV*(R),

s=s1s2…sn,
则Jsx⊆M。由于M是w*-模,故sx∈M,从而x∈MS。故由定理3.7得到MS是w*-模。
命题3.15无挠的可除模是w*-模。
证明由文献[18]知,无挠的可除模是正则性内射模。引用命题2.11与推论3.2即得。
命题3.16每个T(R)-模是w*-模。
证明由每个T(R)-模都是无挠的可除模与引用命题3.15即得。
4 模的w*-包络
我们知道在w-模环境中,一个GV-无挠模M有w-包络,我们同样可以定义GV*-无挠模的w*-包络。
定义4.1设M是GV*-无挠模,令
Mw*={x∈e(M)|存在J∈GV*(R),
使得Jx⊆M}。
则容易看到Mw*是e(M)的子模,称为M的w*-包络。
显然,当M是GV-无挠模时,Mw*⊆Mw。
定理4.2设M是GV*-无挠模,则有:
(1)M⊆Mw*。
(2)Mw*是M的正则性本性扩张。
(3)e(Mw*)=e(M)。
(4)Mw*是w*-模。
证明(1) 显然。
(2) 由定义4.1,Mw*⊆e(M),故Mw*是M的正则性本性扩张。
(3) 显然e(M)⊆e(Mw*)。设0≠x∈e(Mw*)则存在s∈R是非零因子,使得0≠sx∈Mw*。由于Mw*⊆e(M),故存在非零因子t∈R,使得tsx∈M。因此e(Mw*)=e(M)。
(4)设J∈GV*(R),x∈e(Mw*)=e(M),Jx⊆Mw*。记
J=(a1,a2,…,an),
于是aix∈Mw*,故对每个i,有Ji∈GV*(R),使Jiaix⊆M,因此
J1J2…JnJx⊆M。
由于
J1J2…JnJ∈GV*(R),
故x∈e(M),故x∈Mw*,则Mw*是w*-模。
定理4.3设M是GV*-无挠模,则有:
(1) 若N是w*-模,且M⊆N,则Mw*⊆N。
(2) 若M是w*-模,则Mw*=M。
(3) (Mw*)w*=Mw*。
(4) 设A是M的子模,则Aw*⊆Mw*。
(5)I是R的理想,则(IM)w*=(Iw*Mw*)w*。
(6)Mw*/M是GV*-挠模。
(7) 若B是M的子模,且M/B是GV*-挠模,则Bw*=Mw*。
证明(1) 设x∈Mw*,则存在J∈GV*(R),Jx⊆M。因M⊆N,故e(M)⊆e(N),x∈e(M)⊆e(N)。由Jx⊆M⊆N,以及N是w*-模,则x∈N。因此有Mw*⊆N。
(2) 由定理4.2得M⊆Mw*。设x∈Mw*,则存在J∈GV*(R),使得Jx⊆M。由于M是w*-模,故x∈M,因此有Mw*⊆M。则Mw*=M。
(3) 显然Mw*⊆(Mw*)w*。
下证(Mw*)w*⊆Mw*。设x∈(Mw*)w*,则存在J∈GV*(R),使Jx⊆Mw*。由于J有限生成,故存在J1∈GV*(R),使J1Jx⊆M。而J1J∈GV*(R),x∈e(Mw*)=e(M),故x∈Mw*,即有(Mw*)w*⊆Mw*。
(4) 由定理4.2得M⊆Mw*,故A⊆Mw*。由于Mw*是w*-模,再由(1)得Aw*⊆Mw*。
(5)IM⊆Iw*Mw*,故(IM)w*⊆(Iw*Mw*)w*。


(7) 由(4)得Bw*⊆Mw*。另一方面,设x∈Mw*,则存在J1∈GV*(R),使得J1x⊆M。由于M/B是GV*-挠模,以及J1x是有限生成的,故存在J2∈GV*(R),使得J2J1x⊆B,因此有x∈Bw*。从而得到Mw*⊆Bw*。
命题4.4M是无挠模,则Mw*也是无挠模。
证明设S是非零因子乘法集,s∈S,x∈Mw*,有sx=0,则存在J∈GV*(R),使Jx⊆M。故s(Jx)=Jsx=0,而M是无挠模,故Jx=0。由命题2.11,M是GV*-无挠模,故x=0。则Mw*是无挠模。
命题4.5设J是R的有限生成正则理想,则J∈GV*(R)当且仅当Jw*=R。
证明显然J⊆R。因R是w*-模,故Jw*⊆Rw*=R。
设J∈GV*(R)。由J·1=J⊆Jw*,以及Jw*是w*-模,由定理3.7得1∈Jw*。因此有R⊆Jw*。故Jw*=R。
反之,设Jw*=R,则有1∈Jw*。故存在J1∈GV*(R),使得J1=J1·1⊆J。由命题2.3得J∈GV*(R)。
推论4.6设J∈GV*(R),则(JM)w*=Mw*。
证明由定理4.3和命题4.5得
(JM)w*=(Jw*Mw*)w*=(RMw*)w*=(Mw*)w*=Mw*。
命题4.7I是R的真w*-理想,则对任何J∈GV*(R),有JI。
证明若有J∈GV*(R),使得J⊆I,故Jw*⊆I。由Jw*=R,有1∈Jw*⊆I。于是有I=R,这与I是R的真w*-理想的事实矛盾。故JI。
命题4.8若I是R的正则理想,则I是w-理想当且仅当I是w*-理想。
证明必要性是显然的,下面证充分性。
因I是R的正则理想,故I中有非零因子s。
设J∈GV(R),x∈R,Jx⊆I。令J1=(s)+J,则J1∈GV*(R),且J1x⊆I。由于I是R的w*-理想,故x∈I。于是有I是w-理想。
推论4.9R是弱DW环,当且仅当R的任意正则理想都是w*-理想。
命题4.10设M是GV*-无挠模,a∈R,则aMw*⊆(aM)w*。且若a不是M的零因子,则aMw*=(aM)w*。
证明设x∈Mw*,则存在J∈GV*(R),使得Jx⊆M。从而有Jax⊆aM。故ax∈(aM)w*,于是aMw*⊆(aM)w*。
当a不是M的零因子时,显然a也不是Mw*的零因子。故aMw*≅Mw*,则aMw*是w*-模。由定理4.3(1),aM⊆aMw*,则有(aM)w*⊆aMw*。
定理4.11对R-模M,以下各条等价:
(1)M是GV*-挠模。
(2) 设0→A→B→M→0是正合列。若B是w*-模,则Aw*=B。
(3) 存在一个正合列0→A→F→M→0,使得F是w*-模,且Aw*=F。
证明(1)⟹(2)设g:B→M是给定的同态,不妨设A=ker(g)。对任何x∈B,由于M是GV*-挠模,故有J∈GV*(R),使得g(Jx)=Jg(x)=0。因此,Jx⊆A。故Aw*=B。
(2)⟹(3)设
0→A→F→M→0
是正合列,其中F是自由模,从而是w*-模。由条件Aw*=F,
(3)⟹(1)由定理4.3(6)即得。
定理4.12设M是GV*-无挠模,则以下各条等价:
(1)M是w*-模。
(2) 对任何GV*-无挠模A,同态f:A→M可以扩张到Aw*。

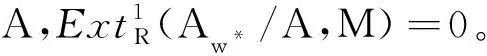
证明(1)⟹(2)设f:A→M是同态。Aw*/A是GV*-挠模,由命题2.11知Aw*/A是挠模。由命题1.4,则存在同态g:Aw*→e(M),使得下图可交换:

对任何x∈Aw*,存在J∈GV*(R),使得Jx⊆A,因此f(Jx)=g(Jx)=Jg(x)⊆M。由于M是w*-模,故g(x)∈M。因此Im(g)⊆M,于是有f可以扩张到Aw*。
(2)⟹(3)设0→A→F→C→0是正合列,其中F是自由模,由定理4.11,Aw*=F,由条件和正合列
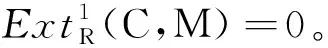
(3)⟹(4)由定理4.3(6)即得。
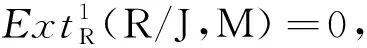
定理4.13设N是GV*-无挠模,B是R-模,A是B的子模。
(1) 若A是GV*-挠子模,则HomR(B/A,N)=HomR(B,N)。

(3) 若B/A是GV*-挠模,N是w*-模,则HomR(A,N)=HomR(B,N)。
证明(1) 由正合列
0→HomR(B/A,N)→HomR(B,N)→HomR(A,N)=0
即得。
(2)由正合列
即得。
(3) 由正合列
即得。
推论4.13若A是GV*-无挠模,N是w*-模,则HomR(A,N)=HomR(Aw*,N)。
证明由定理4.3(6)与定理4.13(3)即得。
5 w*-Noether模与SM环
本节将给出w*-模理论的一些简单的应用。为此,先定义w*-有限生成模的概念。
定义5.1设M是R-模。若存在M的有限生成子模N,使得M/N是GV*-挠模,则M称为w*-有限生成模。
显然GV*-挠模和有限生成模一定是w*-有限生成的。
命题5.2对GV*-无挠模M,以下各条等价
(1)M是w*-有限生成的。
(2)Mw*是w*-有限生成的。
(3) 存在M的有限生成子模B,使得Mw*=Bw*。
证明(1)⟹(2)由假设条件,存在M的有限生成子模B,使得M/B是GV*-挠模。由于
0→M/B→Mw*/B→Mw*/M→0
是正合列,由定理4.3(6)得到Mw*/B也是GV*-挠模。因此,Mw*是w*-有限生成的。
(2)⟹(3)由于Mw*是w*-有限生成的,则存在Mw*的有限生成子模A,使得Mw*/A是GV*-挠模。由于A是有限生成的,故有J∈GV*(R),使得JA⊆M。由定理4.3和推论4.6,(JA)w*=Aw*=Mw*。取B=JA即得所求。
(3)⟹(1)由假设条件与定理4.11,Mw*/B是GV*-挠模,从而M/B是GV*-挠模,因此有M是w*-有限生成的。
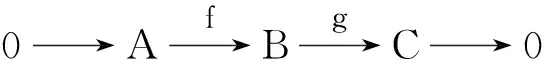
(1) 若B是w*-有限生成的,则C是w*-有限生成的。
(2) 若A和C是w*-有限生成的,则B是w*-有限生成的。

(2) 取有限生成子模A1=(a1,…,am)⊆A,C1=(c1,…,cn)⊆C,使得A/A1与C/C1都是GV*-挠模。取b1,…,bn∈B,使得g(bi)=ci,i=1,…,n。令B1是B的由b1,…,bn生成的子模。若x∈B,则存在J1∈GV*(R),使得J1g(x)⊆C1。于是有J1x⊆f(A)+B1。由于J1x是有限生成的,以及A/A1是GV*-挠模,故存在J2∈GV*(R),使得J2J1x⊆f(A1)+B1。因此有B/(f(A1)+B1)是GV*-挠模。于是得到B是w*-有限生成的。

证明由数学归纳法,只需对n=2的情形证明即可。记M=M1⊕M2,则有正合列
0→M1→M→M2→0
与正合列
0→M2→M→M1→0。
设M是w*-有限生成的,由命题5.3(1),M1和M2是w*-有限生成的。反之,设M1,M2是w*-有限生成的,则由命题5.3(2),得到M是w*-有限生成的。
定义5.5设M是R-模。若M的每个子模是w*-有限生成的,则M称为w*-Noether模。
命题5.6(1) Noether模和GV*-挠模是w*-Noether模。
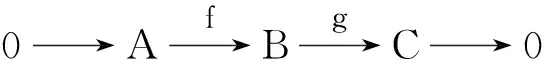

证明(1) 显然。
(2) 不妨设A⊆B,C=B/A。先设B是w*-Noether模。由于A的子模也是B的子模,故A的所有子模皆为w*-有限生成的,因此A是w*-Noether模,且A自身是w*-有限生成的。又由于B/A的每个子模均可以表示为N/A,其中N是B包含A的子模。由于N是w*-有限生成的,故由命题5.3(1),N/A也是w*-有限生成的,因此B/A是w*-Noether模。
反之,设A,C是w*-Noether模。设B1是B的子模,A1=A∩B1,
C1=(B1+A)/A≅B1/(A∩B1)。
则
0→A1→B1→C1→0
是正合列。由条件,A1与C1是w*-有限生成的,由命题5.3(2),B1是w*-有限生成的。于是有B是w*-Noether模。
(3) 由(2)推论即得。
推论5.7设M是GV*-无挠模,则M是w*-Noether模当且仅当Mw*是w*-Noether模。
证明由正合列
0→M→Mw*→Mw*/M→0
与引用命题5.6即得。
设M是R-模,记
L*(M)=(M/torGV*(M))w*。
命题5.8对R-模M,以下各条等价:
(1)M是w*-Noether模。
(2)M/torGV*(M)是w*-Noether模。
(3)L*(M)是w*-Noether模。
证明(1)⟺(2)由正合列
0→torGV*(M)→M→M/torGV*(M)→0
和引用命题5.6即得。
(2)⟺(3)由推论5.7即得。
命题5.9对w*-模M,以下各条等价:
(1)M是w*-Noether模。
(2)M的每个w*-子模是w*-有限生成的。
(3)M有关于w*-子模的极大条件,即M的任何w*-子模的非空集合有极大元。
(4)M有w*-子模的升链条件,即M的任何w*-子模的升链
N1⊆N2⊆…⊆Nn⊆…
都是稳定的。
证明(1)⟹(2)显然。
(2)⟹(1)由命题5.2即得。

(3)⟹(4)设
N1⊆N2⊆…⊆Nn⊆…
是M的w*-子模升链,令Γ={Ni|i=1,2,…}。由假设条件,Γ有极大元,设为Nk。则当n≥k时,有Nn=Nk。故该链是稳定的。
(4)⟹(2)设N是M的w*-子模,取x1∈N,及当n>1时,
xn∈N-(Rx1+Rx2+…+Rxn-1)w*,
于是
(Rx1)w*⊂(Rx1+Rx2)w*⊂…⊂
(Rx1+Rx2+…+Rxn)w*⊂…
是M的w*-子模升链,故此链只能有有限项,即存在n,使得
N=(Rx1+Rx2+…+Rxn)w*,
则N是w*-有限生成的。
回顾模M称为w-Noether模,是指若B是M的子模,则存在B的有限生成子模B1,使得B/B1是GV-挠模。若环R作为R-模是w-Noether模,则称R为w-Noether环。由于GV*-挠模是GV-挠模,故w*-Noether模是w-Noether模。
例5.10w-Noether模未必是w*-Noether模。设J∈GV(R),但JGV*(R)。设M是可数无限个R/J的直和,则M是GV-挠模,从而是w-Noether模。由于R/J不是GV*-挠模,故L*(R/J)≠0,由命题5.9(4),L*(M)=⊕L*(R/J)不是w*-Noether模。从而M不是w*-Noether模。
引理5.11若环R满足GV*(R)=GV(R),即任何GV-理想都是正则理想,则有:
(1) GV-挠模是GV*-挠模,且GV*-无挠模是GV无挠模。
(2) 模M是w*-模当且仅当M是w-模。
证明由这些模类的定义即知。
命题5.12对环R,以下各条等价:
(1)R是w-Noether环。
(2)R作为R-模是w*-Noether模。
(3)R的每个w*-理想是w*-有限生成的。
(4)R有关于w*-理想的极大条件,即M的任何w*-理想的非空集合有极大元。
(5)R有关于w*-理想的升链条件,即R的任何w*-理想的升链都是稳定的。
证明(1)⟹(2)当R是w-Noether环时,由推论1.5知,R的半正则理想是正则理想,则有GV*(R)=GV(R)。由引理5.11,w*-理想都是w-理想,因此,R是w*-Noether模。
(2)⟹(1)显然。
(2)⟺(3)⟺(4)⟺(5)由命题5.9可得。
命题5.12说明了这样一个事实:尽管w-Noether模未必是w*-Noether模,但我们无须定义所谓的w*-Noether环。
回顾模E称为Σ-内射模,是指E是内射模,且E的任意直和还是内射模。众所周知,Noether环有所谓的Cartan-Eilenberg-Bass定理,即R是Noether环当且仅当任意多个内射模的直和是内射模;当且仅当任何内射模是Σ-内射模。2008年Kim-Kim-Park等人[11]证明了在SM整环上也有w-版本的Cartan-Eilenberg-Bass定理,即整环R是SM整环当且仅当任意多个GV-无挠的内射模的直和是内射模;当且仅当任何GV-无挠的内射模是Σ-内射模。2010年王芳贵和张俊[12]把Kim-Kim-Park的结果推广到更一般的w-Noether环上。与这些结果对应,我们有w-Noether环的另一表述形式的Cartan-Eilenberg-Bass定理:
定理5.13(Cartan-Eilenberg-Bass)对环R,以下各条等价:
(1)R是w-Noether环。
(2) 任意多个GV*-无挠的内射模的直和是内射模。
(3) 可数无限个GV*-无挠的内射模的直和是内射模。
(4) 每个GV*-无挠的内射模是Σ-内射模。
证明(1)⟹(2)R是w-Noether环时,由引理5.11,GV-无挠模与GV*无挠模等价,故由定理1.6即得。
(2)⟹(3)显然。
(3)⟹(1)反设R不是w-Noether环,则R有非稳定的w-理想升链
I1⊂I2⊂…⊂In⊂…。

f(a)=(π1(a),π2(a),…,πn(a),…),
于是f(a)∈E,因而f可以扩张为同态g:R→E。记
g(1)=(x1,x2,…,xn,…),xi∈Ei,
且设n≥m时,xn=0。取t>m,a∈I-It。于是πt(a)≠0。又因
f(a)=(π1(a),π2(a),…,πt(a),…)=
g(a)=(ax1,ax2,…,axm,0,0,…),
故有πt(a)=0,矛盾。从而R是w-Noether环。
(2)⟹(4)显然。
(4)⟹(1)由于GV-无挠模是GV*-无挠模,故由假设条件得到每个GV-无挠的内射模是Σ-内射模。由定理1.6,R是w-Noether环。
文献[13]中定义了若R有正则w-理想的升链条件,则称R为SM环。我们也可以用正则w*-理想的升链条件来刻画SM环。
定理5.14对环R,以下各条等价:
(1)R是SM环.
(2)R有正则w*-理想的升链条件。
(3)R的每个正则w*-理想是w*-有限生成的。
(4)R的任何正则w*-理想的非空集合有极大元。
(5)R的每个正则理想是w*-有限生成的。
证明(1)⟺(2)由命题4.8即得。
(2)⟹(3)设I是R的正则w*-理想,若I不是w*-有限生成的,取正则元素x1∈I,及当n>1时,
xn∈I-(Rx1+Rx2+…+Rxn-1)w*,
于是
(Rx1)w*⊂(Rx1+Rx2)w*⊂…⊂
(Rx1+Rx2+…+Rxn)w*⊂…
是R的正则w*-理想升链,但不是稳定的,矛盾。故I是w*-有限生成的。

(4)⟹(2)设
I1⊆I2⊆…⊆In⊆…
是R的正则w*-理想升链。记
Γ={Ii|i=1,2,…},
由条件Γ有极大元In,故当m≥n时,Im=In,因此该链是稳定的。
(3)⟺(5)由命题5.2即得。
推论5.15设R是完全商环,即满足T(R)=R,则R是SM环。
设M是任何R-模,则对任何模簇{Ai},有自然同态
其中
θ([fi])(x)=[fi(x)],x∈M,
fi∈HomR(M,Ai)。
引理5.16(1)θ是单同态,且M是有限生成模时,θ是同构。
(2) 若M是w*-有限生成模,且每个Ai是w*-模,则亦有θ是同构。
证明(1) 参见定理1.7。
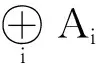
引理5.17设{Ai}是一簇w*-模,F是有限生成的自由模,B是F的w*-有限生成子模,记M=F/B,则
证明由于0→B→F→M→0是正合列,则有下面的交换图:

其中θ1,θ2,δ都是自然同态。由引理5.16知θ1,θ2同构,因此δ同构。
命题5.17对环R,以下各条等价:
(1)R是SM环。
(2) 任意多个GV*-无挠的正则性内射模的直和是正则性内射模。
(3) 可数无限个GV*-无挠的正则性内射模的直和是正则性内射模。
(4) 每个GV*-无挠的正则性内射模是Σ-正则性内射模。

故E是正则性内射模。
(2)⟹(3)显然。
(3)⟹(4)设E是GV*-无挠的正则性内射模。由假设条件,可数无限直和E(∞)是正则性内射模。由定理1.8,E是Σ-正则性内射模。
(4)⟹(1)由于GV-无挠模是GV*-无挠模,故由假设条件得到每个GV-无挠的正则性内射模是Σ-正则性内射模。由定理1.8,R是SM环。
