改进LuGre模型的电磁直线执行器自适应鲁棒控制

2022-11-18谭草黎德祥葛文庆李波陆佳瑜

电机与控制学报 2022年10期

谭草，黎德祥，葛文庆，李波，陆佳瑜

(山东理工大学交通与车辆工程学院，山东淄博 255000)

0 引言

电磁直线执行器相比传统的滚珠丝杆直线传动系统，动力传递路线缩短，响应迅速，具有高效节能的优点[1-2]。以电磁直线执行器为代表的直线直接驱动技术已经成为汽车线控、智能制造等领域研究的热点。

电磁直线执行器是一个非线性强的耦合系统，未经衰减的负载直接作用于执行器，执行器参数的变化也直接影响系统的正常运行，这些因素都给执行器的控制带来困难。从控制问题的角度看，高响应、高精确度是控制的基本问题[3-4]。电磁配气机构等领域要求执行器实现“软落座”，对落座速度要求严格[5-6]；文献[7]针对电磁直线执行器模型的不确定性问题，提出了一种非线性自适应轨迹跟踪的落座控制和一种基于极值搜索的多变量自适应控制；文献[8]为应对变化负载力下的工作需求，提出了一种基于能量法的反馈控制器；摩擦力作为电磁直线执行器中普遍存在的非线性作用，在很多控制问题的研究中被简化为未建模因素或者外部扰动，然而对摩擦力进行建模及补偿对控制器的进一步提升具有重要意义。

从控制算法的角度看，传统的PID控制、解耦控制和极点配置等方法以及现代控制算法如自适应控制、鲁棒控制、预见控制和滑模变结构控制等方法都在执行器控制领域中不断地得到应用[9-10]。其中自抗扰控制将扰动前馈补偿与误差反馈控制相结合，具有不依赖被控对象数学模型的优点，然而非线性因素过多往往造成参数调节困难[11]。文献[12]设计过程基于带宽的概念，降低了参考模型设计和控制参数调节的难度。近年来，基于积分反步的自适应鲁棒方法发展迅速，文献[13]给出了一种基于“积分反步”思想逐步设计非线性控制器的方法。文献[14]提出了半正定反馈形式下的单输入单输出自适应鲁棒控制方法，为了解决该方法不能独立设计控制律和自适应律的缺陷，又在文献[15]提出了期望补偿的自适应鲁棒控制理论。自适应鲁棒控制串联弹性执行器[16]、液压执行器[17]、永磁同步电机[18]等在控制领域展现出了良好的控制性能，为控制系统鲁棒性提供了可行的参考。

为使电磁直线执行器在获得期望的响应与精确度，对动态摩擦力等非线性因素以及外界干扰等具有更好的鲁棒性，本文提出对系统不确定性参数、摩擦状态量进行在线自适应估计；结合摩擦补偿自适应控制律，稳定反馈和鲁棒控制设计基于改进LuGre模型的电磁直线执行器自适应鲁棒控制，并对该方法的稳定性、参数影响、控制性能进行分析，通过仿真和试验验证所提方法的有效性。

1 结构与模型

1.1 结构与原理

本文采用的研究对象为一种高功率密度动圈式电磁直线执行器，为上下对称的圆筒形结构，由外磁轭、内磁轭、永磁体、线圈和线圈骨架等部件组成，如图1所示。电磁直线执行器工作原理详见文献[4]，执行器采用Halbach永磁阵列提高驱动能力，相邻线圈电流方向相反以减小电枢反应，具有功率密度高、响应迅速等优势。

1.2 模型建立

动圈式电磁直线执行器是机械、电路和磁路相互耦合[12]，电路子系统、磁路子系统以及机械子系统构成的方程组如下:

(1)

式中：u为电源电压；ke为反电动势系数；v为线圈运动速度；R为线圈电阻；i为线圈电流；L为线圈电感；Fe为电磁力；N为线圈匝数；B为磁感应强度；l为线圈的有效长度；km为电磁力系数；M为运动部件的质量；x为运动部件的位移；Ff为摩擦力；Fdis为建模误差和其他的外界干扰。摩擦作为机械系统中最常见的一类非线性现象，其动力学具有高度的复杂性和不确定性，不能简单地将摩擦力看作是一个常数。为更好地反映电磁直线执行器机械传动的真实情况，采用了一种改进的LuGre动态摩擦力模型[19]，其数学表达式如下

(2)

式中：α0为鬃毛的刚度系数；z为系统的内部摩擦状态；σ1为鬃毛的微观阻尼系数；Af为库伦摩擦系数；α2为粘滞摩擦系数；vs为Stibeck速度；正定函数g(v)用来描述Stibeck现象；σ0α0为库伦摩擦的量级；σ0(α0+α1)为静摩擦的量级。定义s(|v|)为一非递增的连续函数

(3)

式中l1>l2>0为两个切换速度。考虑电气动力学的建模，其驱动电流i与控制电压u的关系不能简单地化简为正比的关系，由于式(1)电路子系统中第三项相对于其他两项很小，为简化模型可忽略不计。结合式(1)、式(2)，可得到整个控制系统的动力学方程组

(4)

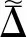
∀θ∈Ωθ,θimin≤θi≤θimax,i=1,…,6。

(5)

(6)

式中：θimax和θimin为已知的常数;δ(x,t)为已知的形态方程；d(t)为未知但有界的时变扰动。

2 控制器设计

2.1 参数自适应设计

2.1.1 模型不确定性参数集自适应律设计

(7)

式中：Γ为一个连续可导且正定对角的自适应律矩阵；τ为自适应函数;p为类滑模变量；ψ的表达式为

(8)

此外，参数自适应不连续的映射函数[21]定义为

(9)

对任意τ的投影映射，可实现以下性质：

∀θ∈Ωθ,θimin≤θi≤θimax,i=1,…,6。

(10)

(11)

2.1.2 时变非线性摩擦状态量自适应律设计

为了解决动态摩擦力模型中状态量z为不可测的问题。需分别对z1和z2进行自适应估计。因此，设计基于映射函数的双重观测器，使其对建模误差有一定的鲁棒性，即有

(12)

式中β1和β2的值分别为：

相应的投影映射函数可以表示为

(13)

式中：z1max=z2max=α0+α1;z1min=z2min=-α0-α1。对任意βj的投影映射，可实现以下性质：

(14)

(15)

式(10)和式(14)意味着参数和状态的估计总是有已知的界。因此，可以综合一定的鲁棒控制律，以保证一般鲁棒性能。此外，式(11)和式(15)的特性能够使用自适应算法来消除参数不确定性的影响，从而大大改善稳态跟踪性能。

2.2 自适应鲁棒控制系统设计

自适应鲁棒控制器包含自适应控制、鲁棒控制和线性反馈控制3个部分，如图2[22]所示。

定义电磁直线执行器的一个类滑模变量p和输出跟踪误差e=x1-xd，并且有

(16)

式中：k1>0为常数增益；xd为电磁直线执行器的参考位移。由式(16)得

(17)

式(17)是一个稳定的收敛速度为k1的传递函数，当p很小或者是趋于0时，e也就会很小或者是趋于0。根据式(4)，对p求导得

(18)

自适应鲁棒控制器[23]设计如下

(19)

式中：ua为自适应模型补偿项；us为鲁棒反馈项；us1为简单的比例反馈，以稳定名义动力学；ks1为一足够大的非线性增益；us2为用来减弱模型不确定影响的鲁棒项，它满足下面的2个条件：

(20)

式中：ε0和ε1为任意小的常数。一种满足式(20)的us2为

(21)

式中：ks2为一足够大的非线性增益；h0、h1和h2[24]为满足以下条件的任意光滑边界函数：

(22)

式中‖‖2代表欧几里得范数。

2.3 控制器的稳定性证明

a)观测器经过有限时间t0内收敛时，选择Lyapunov函数为

(23)

证明：对式(23)进行求导并结合式(15)得

(24)

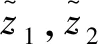
(25)

b)控制器经过有限时间t0内收敛时，选择Lyapunov函数为

(26)

并且它有界于

exp(-λt)]。

(27)

其中λ=2ks1/θ1max。

证明：对式(26)进行求导并结合式(20)得

(28)

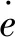
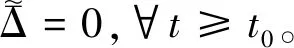
证明：选择Lyapunov函数为

(29)

对式(29)进行求导，得

(30)

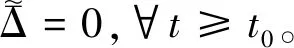
(31)

由于g(x2)>0,s(|x2|)≥0和us2p≤0得

(32)

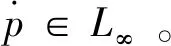
3 控制性能分析

3.1 参数影响分析

为研究控制器参数与控制性能的相关性关系，通过相关系数矩阵进行相应的数据分析，基于皮尔逊相关系数来研究多变量的相关性问题，具体公式[25]为

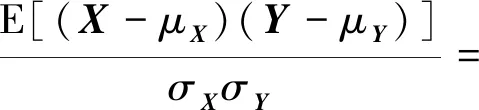
(33)

式中：E(·)为数学期望；μX为样本X的均值；σX为样本X的标准差；μY为样本Y的均值;σY为样本Y的标准差。经计算可得到各个控制参数对系统性能影响的相关系数矩阵如图3所示，图中纵坐标表达式为

(34)

式中：JITAE为时间与误差绝对值乘积的积分，它反映控制系统在转换状态时，以最小代价的损失实现控制目的；tr为系统的响应时间，定义为系统从10%到90%的参考位移所经历的时间，它反映控制系统的响应速度；σ(%)为超调量；gi为θi对应的正定对角矩阵系数。

从图可知，σ(%)与k1负相关度最大，tr与k1正相关度最大，k1对JITAE也有明显影响。σ(%)与ks1的正相关度最大，与ks2的正相关度次大；tr、JITAE与ks2的负相关度最大，与ks1的负相关度次大。ks1和ks2为自适应鲁棒控制中的两个关键控制参数，这与实际控制规律吻合。执行器工作中不可避免地会产生系统参数变化，在确定控制参数之后，图4进一步分析系统参数对系统控制性能的影响。为了比较，考虑PID算法[26]

(35)

式中Kp、Ki、Kd分别为比例、积分和微分因子。

自适应鲁棒控制中线圈电阻对σ、tr与JITAE影响都最大，执行器应用中应合理设计散热方案以避免温升带来的电阻变化；PID控制中，线圈电阻对k1与JITAE影响最大，电磁力系数对σ影响最大。系统动质量、线圈电阻以及电磁力系数在自适应鲁棒控制中对控制性能的影响显著小于在PID控制中，说明自适应鲁棒控制对系统参数变化敏感程度较低。

3.2 干扰抑制分析

为分析系统对负载扰动的抑制能力，以式(4)为研究对象，分别进行式(35)的PID控制和式(14)中的鲁棒控制项us的鲁棒控制，并与自适应鲁棒控制进行对比分析。在达到目标位移xd=5 mm之后(25 ms时)，负载从0 N突变为100 N，不同控制算法下系统响应如图5所示。由于负载扰动，稳定在目标位移的执行器迅速偏离目标位移；PID控制、鲁棒控制和自适应鲁棒控制偏离目标位移的最大值分别为0.25、0.12和0.05 mm，调节过程中自适应鲁棒控制位移偏移的最大值显著小于鲁棒控制与PID控制；在反馈控制作用下执行器重新回到目标位移并保持稳定的时间为6.5 ms，相比于PID控制和鲁棒控制分别缩短了110.7%、16.9%。显著小于鲁棒控制与PID控制的调节时间。自适应鲁棒控制外部负载扰动情况下调整能力优于鲁棒控制与PID控制。

图6为系统在白噪声干扰下的轨迹跟踪曲线对比，期望位移xd=0.008sin(8πt)m，由图可知，PID控制、鲁棒控制和自适应鲁棒控制在白噪声干扰下都能实现对目标位移的渐进跟踪，最大误差分别为1.13、0.79和0.24 mm，自适应鲁棒控制的跟踪误差与稳定性显著优于PID控制和鲁棒控制。说明在电磁直线执行器运动过程中受到持续的外界信号干扰时，仍然能有效地消除摩擦力带来的不利影响，从而提升控制精确度和系统稳定性。

4 试验与分析

为验证提出算法对电磁直线执行器的有效性，搭建了如图7所示的试验平台，通过基于DSP2812的控制器实现控制算法，控制器集成了电流传感器与H桥驱动模块，执行器的位移由激光位移传感器实时检测并显示在上位机中。被控的电磁直线执行器工作行程为20 mm，线圈256匝、电阻为1.18 Ω，动质量为0.250 kg。

为验证所设计摩擦补偿控制算法的有效性，将所该算法与PID控制方法和鲁棒控制方法在相同的试验条件下进行比较。设置期望xd=15 mm的阶跃位移，电磁直线执行器不同控制算法下的系统响应曲线如图8所示。

由试验结果可知，由于起步阶段的动态滞后现象，系统运动速度较缓慢。随着控制器的控制作用，系统快速运动，并朝着目标位移靠近。最终，PID控制、鲁棒控制和自适应鲁棒控制都能实现系统对位置阶跃信号的不超调跟踪，稳态误差趋于0，系统位置响应误差满足系统静态跟踪精确度要求。自适应鲁棒控制相对于鲁棒控制和PID控制的时间分别缩短了6.9和9.8 ms。在保障稳态精确度前提下，自适应鲁棒控制的响应速度更快。由图8(b)可知，整个跟踪过程中，辨识出的动态摩擦内部状态收敛于之前离线辨识出的结果。自适应鲁棒控制对非线性摩擦力的补偿效果，显著大于PID控制和鲁棒控制。对比可知，自适应鲁棒控制能够有效克服非线性摩擦对控制系统的影响，更好地消除摩擦带来的反应迟缓，实现快速跟踪。

图9为不同控制算法下电磁直线执行器斜坡响应结果曲线，不同控制算法下，执行器都能在10 mm内跟踪目标曲线，证明了电磁直线执行器快速响应的特性。其中，本文提出的控制算法下，执行器在5 mm以内跟踪目标曲线，且稳态误差趋近于0，在响应速度与控制精确度上优于PID控制以及鲁棒控制。

图9(b)为自适应鲁棒控制下控制器输出占空比与执行器线圈电流曲线，响应之初输出占空比为满占空比，从而实现执行器的快速响应；随后占空比迅速调节为负值，线圈电流随之变为负值以实现执行器动子的减速；最后占空比和电流保持在固定值，执行器动子匀速运动、稳定跟踪目标斜坡曲线。

为验证自适应鲁棒控制的轨迹跟踪性能，设置期望位移xd=0.008sin(8πt)，电磁直线执行器不同控制算法下的轨迹跟踪曲线如图10所示。在第一个峰值处，自适应鲁棒控制相位滞后时间和相对误差分别为0.1 ms和0.1%；PID控制和鲁棒控制相位滞后时间分别为0.7和0.3 ms，相对误差分别为3.7%和2.8%。随后，自适应鲁棒控制相位滞后时间和相对误差逐渐趋近于0。整个跟踪过程中，自适应鲁棒控制的跟踪误差与相位滞后时间，显著小于PID控制和鲁棒控制下的跟踪误差；对比可知自适应鲁棒控制不仅能够提高系统的瞬态响应性能，而且能够以更高的精确度跟踪连续位置指令，更好地消除摩擦带来的跟踪误差，实现平稳跟踪。