永磁同步电机改进滑模无位置传感器控制

康尔良，陈健

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080)

0 引 言

随着“双碳”目标的提出和新能源行业的快速发展，永磁同步电机(permanent magnet synchronous motor，PMSM)因具有结构简单和效率高等优点，被广泛应用在日常生活和工业生产等领域中。PMSM最常用的控制方法之一是磁场定向控制，通常需要用编码器等获取准确的转速和转子位置信息。但是，位置传感器的安装易受环境影响，会增加系统成本和降低系统可靠性[1-2]。

因此，永磁同步电机无位置传感器控制一直是被关注的热点问题[3]。在众多的估计方法中，滑模观测器法(sliding mode observer，SMO)因结构简单和鲁棒性强等优点被广泛应用在PMSM中高速无位置传感器控制系统中[4-7]。

针对滑模观测器中sign函数的存在会造成抖振问题[8]，文献[9-13]中分别采用不同的连续函数取代滑模观测器中的sign函数作为切换控制函数，从而减小抖振，提高转速和转子位置估计精度。文献[14-19]中采用超螺旋滑模观测器(super twisting algorithm-sliding mode observer，STA-SMO)对转速估计。相比采用sign函数作为切换函数的一阶滑模观测器而言，STA-SMO是将sign函数放在滑模变量的高阶导数中，控制率中会含有sign函数的积分项，又因为积分本身具有滤波作用，因此可以实现对抖振的抑制。

但是，较大的固定滑模增益值会降低观测器在低速时的估计精度，而较小的固定增益可能会造成高速时观测器的不稳定。而且，在基于STA-SMO的无位置传感器控制系统中，常规PI控制器存在鲁棒性差和动态响应慢的问题[20]。

因此，出于提高转速估计精度和控制系统鲁棒性的目的，本文提出一种变增益的STA-SMO，同固定增益的STA-SMO相比，所提方法可以提高低速时转速估计精度。根据初等扰动观测器的基本原理，设计出一种新型转矩观测器，将估计出的转矩值应用到基于新型趋近律的滑模转速控制器中。相比PI控制器，基于新型趋近律和转矩观测器的控制器可以极大提高系统的动态响应和鲁棒性。

1 永磁同步电机的数学模型

因PMSM是一个非线性强耦合的时变系统，常假设磁路不饱和，气隙磁场空间中呈正弦分布，三相定子绕组对称，忽略涡流和磁滞损耗等因素达到简化分析过程的目的。在以上假设条件下，PMSM在α-β轴下的数学模型可以表示为：

(1)

式中：iα、iβ是α-β轴下定子电流值；uα、uβ是α-β轴下定子电压值；Rs和Ls是定子电阻和电感；α-β轴下的反电动势eα=-ωeψfsinθe、eβ=ωeψfcosθe，ωe和θe是电角速度和位置角；ψf是永磁体磁链。忽略电机运行过程中电感值的变化，即假设α-β轴下的电感值Ls是常数。

2 超螺旋滑模观测器设计

2.1 超螺旋算法原理

超螺旋滑模理论是滑模控制发展中的重要成果之一，文献[21]中已证明超螺旋算法具有稳定性和有限时间收敛性，最基本的形式为：

(2)

文献[21]中证明，如果式(2)中的扰动ρ1、ρ2全局有界，即

|ρ1|≤δ1|x1|1/2；ρ2=0。

(3)

而且k1、k2增益满足：

(4)

则系统将在有限时间内收敛到滑模面，δ1是大于0的常数。

2.2 超螺旋滑模观测器设计

基于上述超螺旋算法设计电流观测器，将α-β坐标系下的电流当作状态变量，即分别将x1=iα和x1=iβ代入式(2)中，则式(2)可以写成：

(5)

扰动项ρ1为：

(6)

将式(6)代入式(5)可以得到电流观测器方程为：

(7)

将式(6)代入式(3)中，式(3)可以重写成：

(8)

对于足够大的δ1，式(8)很容易满足。

由式(7)减去式(1)得：

(9)

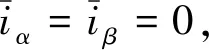
(10)

2.3 变滑模增益STA-SMO设计

虽然STA-SMO可以减小抖振，但是为保证电机在高速域的稳定运行，滑模增益值必须足够大且满足式(4)中的稳定性条件。但当电机运行在低速域时，较大的增益值会加剧观测器的抖振，降低转速的估计精度。同理，较小的滑模增益可能造成观测器高速范围内的不稳定。

因此，为提高STA-SMO的转速估计精度，本文提出一种如图1所示的滑模增益值随估计转速变化的变增益STA-SMO，滑模增益值为：

(11)

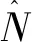
因为在较短的采样周期内，可认为转速是保持不变的，所以在稳定性分析时将式(11)中的k1、k2看作常数。根据电流观测器方程和超螺旋算法原理，α轴扰动项ρ1可以表示为

(12)

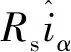
(13)

由以上可知，全局有界性条件可以重写成

(14)

(15)

(16)

必定存在足够大的常数σ2满足式(16)。

由以上分析可知，k1、k2满足稳定性条件(4)，即证明提出的基于变增益的超螺旋滑模观测器是稳定的。

3 新型滑模控制器设计

3.1 基于新型趋近律的转速控制器设计

针对基于STA-SMO的控制系统中PI转速控制器的鲁棒性差和动态响应慢的问题，提出一种新型滑模趋近律：

(17)

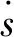
以下给出新型趋近律的稳定性证明。

选择李雅普诺夫函数

(18)

对式(18)求导得

(19)

以上提出的新型滑模趋近律满足滑模到达条件，可以保证运动轨迹在有限时间到达滑模面。

基于新型趋近律的滑模转速控制器设计步骤和基于传统趋近律的转速控制器的设计步骤相同。

首先，设计滑模切换面

(20)

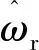
对滑模切换面求导得

(21)

基于STA-SMO的控制系统中PMSM的机械运动方程是

(22)

式中：J是转动惯量；iq是q轴电流；TL是负载转矩；B是阻尼系数。

将式(22)代入式(21)可得

(23)

将式(17)新型趋近律代入上式整理得

(24)

式(24)是基于新型趋近律设计的永磁同步电机滑模控制器输出，即q轴电流的给定值，实现对永磁同步电机的转速控制。

3.2 新型转矩观测器设计

根据文献[22]中的扰动观测器模型，PMSM新型转矩观测器可以设计成

(25)

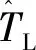
转矩的估计误差可以表示为

(26)

将式(22)代入式(26)可得

(27)

因在采样周期内TL是定值，系统的动态误差方程为

(28)

式(27)中含有估计机械角速度的导数项，而求导会导致估计转矩值中出现噪声，会影响观测结果，从而对控制系统的鲁棒性造成影响。

因此，将式(27)中含有导数项的部分看作一个整体的中间变量，即

(29)

则有

(30)

改进后的观测器方程为：

(31)

根据李雅普诺夫理论对观测器稳定性分析

(32)

对式(32)求导得

(33)

将式(28)代入式(33)得

(34)

当满足K<0，转矩观测器是稳定的。

最终，设计的转速滑模控制器的电流给定值是

(35)

基于变增益的STA-SMO和改进滑模转速控制器的控制系统框图如图3所示。

4 仿真和实验验证

4.1 改进滑模无位置传感器控制仿真结果

为验证所提方法的有效性，在MATLAB/Simulink中，分别搭建基于固定增益值和基于变增益值的STA-SMO控制系统仿真模型，两者都采用正交锁相环的方法获取转速和转子位置，速度环都采用PI控制器。固定超螺旋滑模观测器的滑模增益值k1=40，k2=200 000；变滑模增益值σ1=0.04，σ2=0.2；锁相环的参数kp=2 000，kI=500；PI转速环控制器的参数Kp=0.3，KI=0.7。

仿真中采用固定步长2e-7，仿真时间设置1 s，仿真和实验中PMSM的参数如表1所示。

表1 PMSM模型的参数

图4是空载0时给定转速300 r/min和0.5 s时给定转速1 000 r/min，固定增益的STA-SMO转速估计误差，由图中可以看出低速300 r/min时因为较大增益值的存在，估计误差最大可达1.5 r/min。

由图5变增益STA-SMO转速估计误差和图4对比得，低速300 r/min时最大估计误差仅有0.15 r/min，明显提高低速时估计精度。

由图6固定增益和图7变增益STA-SMO转子估计误差可知，两者都有较高的转子位置估计精度，最大误差仅有0.28 rad，但低速时变增益STA-SMO转子位置估计精度更高。因为变增益STA-SMO中σ1、σ2的值是在估计转速1 000 r/min时计算出的，所以当给定转速是1 000 r/min时，固定增益和变增益的k1、k2值相等，可保证高速时STA-SMO是稳定的。

图8和图9是变增益的k1和k2的波形图。

由图8和图9中变增益值放大部分可知，随估计转速的增加，滑模增益逐渐增大，从而减小电机在低速时过大的滑模增益值造成抖振的现象，同时高速时足够大的滑模增益值可以保证STA-SMO的稳定性。

图10和图11是变增益STA-SMO估计的转速和转子位置同实际的转速和转子位置对比图。

由图10放大部分可知，在极短的时间内变增益的STA-SMO可实现对实际转速的准确估计。而且，由图4的转速估计误差可看出，在给定转速300 r/min时，最大估计误差有15 r/min。在0.5 s，给定转速是1 000 r/min时，转速估计误差仅有5 r/min。同样，由图11可得出，在整个1 s仿真时间内，变增益STA-SMO能够始终保持对转子位置的精确估计。

为进一步验证突加减负载时变增益STA-SMO转速和转子位置估计精度，在0和0.5 s给定转速分别是300 r/min和1 000 r/min的基础上，0.2 s时和0.6 s时分别加载4 N·m和卸载。

由图12可知，在突加减载时，转速估计误差仅有最大0.6 r/min的变化，而且在极短的时间内即可恢复。同样，由图13可得，加减负载对转子位置估计精度影响较小，证明所提出的变增益STA-SMO具有一定的鲁棒性。

由图14可知，当0.2 s突加负载时，估计转速和实际转速下降12 r/min，且在0.3 s内未能恢复到给定转速。同样在0.6 s突减负载时，转速上升9 r/min且恢复时间较长。由以上仿真结果可知，变增益的STA-SMO在加减负载时依旧能够保持对转速和转子位置的精确估计，但是PI转速控制器存在鲁棒性差和动态响应慢的问题。

图15是采用新型负载转矩观测器估计转矩值和实际转矩值的对比图。

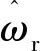
图16是采用改进滑模转速控制器的无位置系统中估计转速和实际转速的对比图。

由图16和图14相比可知，基于新型转矩观测器和新型趋近律的滑模转速控制器在0.2 s突加负载时，转速只有不到3 r/min的下降而且恢复时间只有3 ms。在0.6 s突减负载时，转速虽较低速时波动更大，但依旧能够迅速达到给定转速，而且在整个过程中估计转速始终保持对实际转速的精确估计，证明所提出的变增益的STA-SMO和新型趋近律的滑模控制器的理论正确性。

4.2 改进滑模无位置传感器控制系统实验验证

搭建如图17所示的基于DSP28335的实验平台，验证改进滑模无位置传感器控制系统的正确性。为验证低速时所提方法的可靠性，给定转速是400 r/min，在3 s时突加4 N·m的负载。图18是基于以上实验条件下实际转矩和估计转矩波形图，图19和图20分别是转速估计误差和转子位置估计误差，图21是估计转速波形图。

图18表明当3 s突加负载时，新型转矩观测器可以在1 s时间内实现对负载转矩的观测，而且具有较高的观测器精度，证明所提新型转矩观测器理论是有效的。

由图19和图20变增益STA-SMO转速估计误差和转子位置误差可知，当在低速稳定运行时，估计误差不到1 r/min，转子位置误差保持在0.2 rad，证明变增益的STA-SMO具有较高的估计精度。

由图21可得，在0.6 s时估计转速达到给定转速，超调较小。当3 s突加负载时，估计转速虽具有一定程度的下降，但很快可以达到给定转速并保持稳定运行，证明基于新型转矩观测器和新型趋近律的滑模转速控制器动态响应快，具有强鲁棒性。由以上的实验结果可知，本文所提出的改进滑模无位置传感器控制系统具有可行性。

5 结 论

针对固定滑模增益STA-SMO低速时转速估计精度低和基于STA-SMO的无位置传感器控制系统中PI转速控制器鲁棒性差的问题，本文提出一种改进滑模无位置传感器控制方法。通过仿真和实验得出以下结论：

1)相较固定增益的STA-SMO，增益值随转速变化的变增益STA-SMO可以减小低速时转速和转子位置估计误差，同时保证高速时观测器的稳定性。

2)基于新型转矩观测器和新型趋近律设计的滑模转速控制器在加减负载时，相较PI转速控制具有更快的动态响应和更强的鲁棒性，而且在基于变增益STA-SMO估计出的机械角速度下，新型转矩观测器可以实现对负载转矩的精确估计，从而保证新型滑模控制器具有更高的控制精度。

3)提出的改进滑模无位置传感器控制方法，不仅可以提高转速和转子位置的估计精度，还可以突加减负载时保持对给定转速的准确跟踪，从而实现高精度控制。