外转子永磁同步电机径向电磁力分析与抑制

边旭，纪毅，梁艳萍

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080)

0 引 言

近年来，外转子永磁同步电机在新能源车中的应用越来越广泛，其产生的电磁噪声是整车主要的噪声来源之一，如何减小电机的电磁噪声是车用电机设计过程中的关键问题，对电动车整体的舒适性以及安全性具有重要意义[1]。径向电磁力引起的电磁振动是外转子永磁同步电机电磁噪声的主要来源，因此，有必要对其径向电磁力进行准确分析并进行抑制。

径向电磁力的分析计算及其抑制一直是电机研究的热点问题。文献[2]针对电动汽车用永磁同步电机，提出一种新型隔磁桥，通过对比验证了该结构能够显著减小电机的径向电磁力。文献[3]通过转子分段斜极及开辅助槽的方法抑制电机的径向电磁力。文献[4]对内置式永磁同步电机使用转子开辅助槽的优化设计，优化结果显示电机在优化前后的径向电磁力降低明显。文献[5]研究了转子不同分段斜极对电机振动噪声的影响，并得到双边斜极对径向电磁力的抑制效果最为明显的结论。文献[6]研究了电机转子动态及静态偏心下的电磁振动，结果显示其会产生额外的径向电磁力，且这些力的频率及空间阶次会更接近于定子低阶模态，从而加剧电磁振动。文献[7]研究了不同极槽配合下电机的电磁振动，对于由内部电磁力所引起的定子振动，当电机极数相同时，每极的槽数为分数时比整数时的径向电磁力要大，从而振动更大。文献[8-9]研究了外转子永磁同步电机径向力的高频谐波对电机振动噪声的影响。目前，国内外对电机径向电磁力分析计算及抑制方法的研究主要针对内转子电机，对外转子电机研究较少。

本文以一台3 kW外转子分数槽永磁同步电机作为样机，对其径向电磁力来源及阶数进行理论分析，以降低径向电磁力为目的，提出一种齿顶偏心结构，建立电机齿顶偏心前后的有限元模型，对径向电磁力进行分析对比，并通过样机实验对仿真结果进行验证。

1 外转子分数槽永磁电机基本结构

本文所研究的外转子永磁同步电机基本数据如表1所示。

表1 电机基本数据

外转子永磁同步电机结构如图1所示。其定子位于内部，而转子位于外部，永磁体位于转子铁心与护套中间。本台电机为分数槽集中绕组,其绕组分布如表2所示。

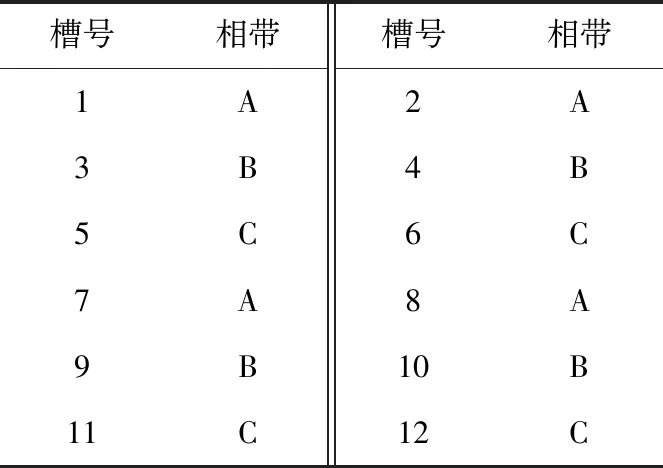
表2 分数槽集中绕组分布表

2 径向电磁力波理论分析

2.1 径向电磁力波来源分析

在电机所产生的振动噪声来源中，电机的电磁振动噪声是主要来源。产生电磁振动噪声的主要原因是电机的定子受到径向电磁力的作用。根据麦克斯韦方程，永磁同步电机受到的径向电磁力密度瞬时值[10-11]可以表示为

(1)

式中：Br(θ,t)为电机的径向气隙磁密；Bt(θ,t)为电机的切向气隙磁密；θ为空间角度；t为时间；μ0为真空下的磁导率。

由于径向气隙磁密远大于切向气隙磁密，故切向气隙磁密可以忽略不计[12]，则径向电磁力密度的表达式可化简为

(2)

进一步，如果假设电机定子铁心磁阻忽略不计，则径向气隙磁密[13]可以表示为

Br(θ,t)=f(θ,t)λ(θ,t)。

(3)

式中：f(θ,t)为电机的气隙磁动势；λ(θ,t)为气隙磁导。

将式(3)代入式(2)中，且经傅里叶变换为

Fr=∑n∑ωFn,ωcos(ωt-nθ)。

(4)

式中：n为力波阶数；ω为n阶力波角频率；Fn,ω为力波幅值。

由电磁力所产生的电磁振动可以表示为

(5)

式中A为定子铁心变形量。

由式(5)可以得到，电机的电磁振动与力波阶数的四次方成反比，与力波幅值成正比，所以应重点关注力波阶数较小且力波幅值较大的力波。

2.2 径向电磁力波阶数分析

对于永磁同步电机，其气隙磁密是由永磁体产生的磁场以及电枢绕组产生的磁场两者共同作用所产生的。永磁同步电机的极槽配合以及绕组结构的不同影响电枢磁动势的谐波含量，最终所产生的力波阶数也不同。本文主要讨论分数槽集中绕组的径向电磁力波阶数的计算。

电机每极每相槽数表达式为

(6)

式中：Z为电机槽数；p为电机极对数；m为电机相数。

由电枢磁场产生的磁势谐波次数为

(7)

式中k=0,±1,±2,…。

本文样机的类型为极数与槽数满足Ns=2p±2的分数槽电机，这是一类在工程中常用的集中绕组电机。对于这类电机，其每极每相槽数又可以表示为

(8)

由于p±1不能被p整除(当p≠1时)，此时d与极对数p在数值上一致。此时电枢反应磁场谐波阶数可以表示为

v=6k+p。

(9)

由永磁体磁场产生的磁势谐波次数为

μ=(2l+1)p。

(10)

式中l=0,1,2,…。

电机电枢磁场产生磁动势的v次谐波与永磁体磁场产生磁动势的μ次谐波相互作用，所产生的电磁力波阶数为

r=μ±v。

(11)

该阶数对应的电机频率为

F=(μ±1)f。

(12)

式中f表示电源频率。

对于本文研究的样机，忽略产生的高阶力波，电机电枢磁场产生磁动势的v次谐波与自身作用产生的径向电磁力波阶数如表3所示，永磁体磁场产生磁动势的μ次谐波与自身作用产生的径向电磁力波阶数如表4所示，永磁体磁场产生磁动势的μ次谐波与电机电枢磁场产生磁动势的v次谐波作用产生的径向电磁力波阶数如表5所示。

表3 电枢反应磁场产生的径向电磁力波阶数

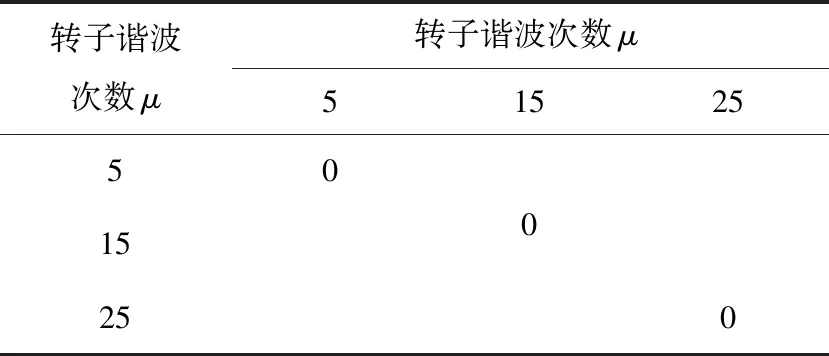
表4 永磁体磁场产生的径向电磁力波阶数

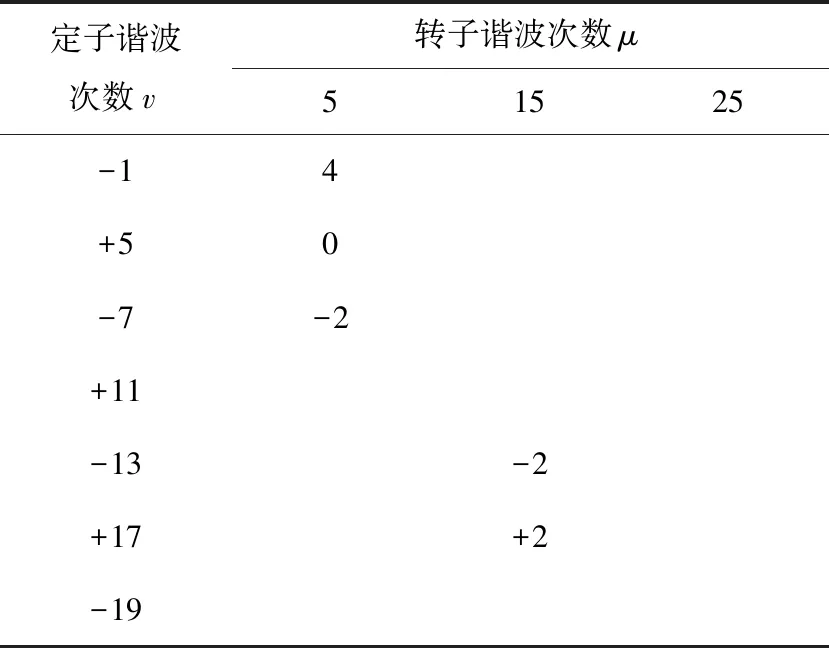
表5 永磁体磁场与电枢反应磁场产生径向电磁力波阶数

从前文的分析可知，幅值较大的低阶电磁力对电机的振动噪声影响最大，结合表5可以得出，电机的0阶电磁力、2阶电磁力以及4阶电磁力对电机的影响最大。

3 径向电磁力波仿真与抑制

本文研究的外转子永磁同步电机的二维模型如图2所示。

本文提出一种定子齿顶偏心的方法对电机的径向电磁力进行抑制。定子齿顶偏心示意图如图3所示。电机未采用偏心结构时，定子齿顶弧线的圆心在O点(与转轴圆心重合)，而采用偏心结构后，定子齿顶弧线的圆心偏移到O′点，其中h代表偏心尺寸。考虑到工艺可行性及电机性能，偏心尺寸选为23 mm。

当电机的定子齿顶不偏心时，其气隙磁密的分布为

(13)

式中：hm为充磁方向长度；Bδ表示永磁体剩磁；δ为气隙长度。

而电机定子齿顶采用偏心结构后，电机气隙磁密的表达式为

(14)

根据图3可以得到定子齿顶偏心时的气隙长度为

(15)

式中：R2为定子外径；θ为定子齿中心线与某一指定永磁体磁极中心线之间的夹角。

通过电机的定子齿顶偏心，使得气隙结构变得不规则，改变了气隙磁密的谐波，进而对电机的径向电磁力进行影响。对比齿顶偏心前后的气隙磁密及其谐波含量即可论证齿顶偏心方法的有效性。

分别建立齿顶偏心前后电机二维瞬态时步有限元模型，并进行额定负载运行工况时的电磁仿真，图4为电机齿顶偏心前后负载工况下的径向气隙磁密曲线图。可以看出，当电机未采用偏心结构时，电机的径向气隙磁密会存在一定的波形畸变且波动较大，而采用了齿顶偏心结构后，会使得电机的径向气隙磁密在原畸变处的畸变降低，有效地增加了波形的正弦性。

图5为负载工况下电机径向气隙磁密的谐波分解图。可以看出，在采取齿顶偏心结构后，电机气隙磁密的1次、5次以及7次谐波含量会降低较为明显，经过计算分别降低了2.95%、9.6%、10.6%。由式(2)可知，电机的径向电磁力密度与径向气隙磁密的二次方成正比，当电机的径向气隙磁密谐波含量降低时，电机的径向电磁力密度也将有所降低。

图6和图7为电机采用齿顶偏心结构前后的径向电磁力波密度时空分解图。从图6可以看出，电机径向电磁力波主要集中在空间0阶时间0阶、空间2阶时间2阶以及空间4阶时间4阶。空间0阶4倍频时幅值较低，从而对电机振动影响较小，而4阶4倍频时幅值较大，所以最终得出，4阶4倍频电磁力对电机的振动噪声影响最大，可以从降低这一阶力波的幅值入手降低电机的振动噪声。

对比图6和图7可知，电机在采用齿顶偏心结构前后，偏心前空间分解较大的空间0阶时间0阶、空间2阶时间2阶以及空间4阶时间4阶分别降低了7.16%、4.68%、10.33%，结构改变后降低效果明显，验证了齿顶偏心结构对径向电磁力抑制的有效性。

4 样机实验

为了验证仿真结果的可靠性，进行了样机空载工况和额定负载工况的实验测试。样机采用了齿顶偏心结构，偏心尺寸为23 mm。样机及样机实验平台如图8所示。

样机在稳定运行后，700～704 ms周期内的空载反电势、A相电枢电流与仿真结果对比如图9所示。经过计算，样机空载反电势与模型仿真反电势的误差为3.35%，样机A相电枢电流与模型仿真电枢电流的误差为5.5%，均在误差允许范围内，证明了模型的有效性。

5 结 论

本文以一台3 kW外转子分数槽永磁同步电机为样机，对其径向电磁力的来源、阶数进行理论分析。并以降低电机径向电磁力为目的，提出一种新型的齿顶偏心结构，得到以下结论：

1)对于外转子分数槽永磁同步电机，径向电磁力是由永磁体磁场与电枢绕组磁场共同作用产生的。其力波阶数较小且力波幅值较大的径向电磁力谐波会对电机的振动噪声产生较大影响。对于本文样机，0阶电磁力、2阶电磁力以及4阶电磁力对电机的振动噪声影响最大。

2)采用齿顶偏心结构后，在额定负载工况下，电机径向气隙磁密的1次、5次以及7次谐波含量会得到较为明显的降低，其分别降低了2.95%、9.6%、10.6%。而对径向电磁力，其幅值较大的空间0阶时间0阶、空间2阶时间2阶以及空间4阶时间4阶分别降低了7.16%、4.68%、10.33%，该方法对径向电磁力的抑制效果较好。