实心定子磁悬浮轴承功率放大器稳定性研究

纪历，马雪晴，陈震民

(1.杭州电子科技大学 信息工程学院，浙江 杭州 310011； 2.浙江中源磁悬浮技术有限公司，浙江 杭州 310011)

0 引 言

磁悬浮轴承是通过定子铁心与转子铁心之间的磁场力将转子无接触地悬浮起来的一种新型轴承，由于不存在机械接触，其与传统机械轴承相比具有明显的优越性[1-4]。完整的磁悬浮轴承系统通常由磁悬浮轴承机械部分(定转子)、位移传感器、控制器以及功率放大器组成。其中功率放大器用来控制定子线圈中的电流，从而产生磁场力使转子稳定悬浮，其性能对于磁悬浮系统至关重要。

通常情况下，磁悬浮轴承的定、转子均采用叠片结构以减小磁路中的涡流效应，进而减小损耗、提高效率。然而叠片结构本身工艺复杂，生产效率低下，此外考虑磁悬浮轴承对加工精度的要求，冲片加工得到的定子叠片在装配后通常还需要进行二次精加工，多道工序延长了磁悬浮轴承的加工周期，阻碍了磁悬浮产品的批量生产。若采用实心铁磁材料加工定子，则可以显著地提高生产效率，但是实心结构有较大的涡流效应，一方面导致发热损耗，一方面会对磁悬浮系统的控制造成负面的影响。

文献[4-6]对磁悬浮系统的损耗进行分析，可知铁心本身的损耗相对于磁悬浮设备(如磁悬浮鼓风机、磁悬浮压缩机)的功率来说并不高，若具有良好的散热条件，定子温升完全可以控制在可接受的范围。但其对控制的影响不能忽略，一个典型的例子就是导致控制电流的高频振荡。关于电流的高频振荡，现有研究普遍认为其由开关功率放大器的非线性导致，文献[7-14]针对功率放大器或变换器的非线性模型进行研究，文献[15-16]证明在磁悬浮功率放大器中存在分岔及混沌现象。文献[17-18]研究了功率放大器调制技术及由于不同的载波形式产生的失效机制。但较少研究关注由于负载特性变化引起的系统不稳定及振荡。

本文着重研究了实心定子结构对磁悬浮功率放大器稳定性的影响，考虑涡流效应建立了负载线圈的数学模型，并计及功率放大器本身的非线性特性及数字延时研究了励磁电流自激振荡的机理。在此基础上提出励磁电流控制系统稳定性的分析方法及控制器的设计原则，并通过仿真与试验对提出的理论进行验证，所得结论能够为磁悬浮技术在工业中的推广应用提供理论依据。

1 磁悬浮励磁控制系统数学模型

磁悬浮功率放大器及励磁电流控制系统的原理如图1所示。该系统主要由控制器C(s)、PWM调制器、功率放大器主电路KV、定子线圈负载G(s)和电流互感器KS组成。

1.1 功率放大器的数学模型

磁悬浮控制系统中最常用的功率放大器是基于H桥的三电平变换器[16]。其主电路拓扑结构如图2(a)所示，其中主电路由电压源E、开关管S1～S4及负载组成。S1(S2)与S3(S4)互补导通，其负载等效为L和R串联的形式。根据S1～S4不同的开关情况，该变换器有三种工作状态：

状态1：开关S1与S4导通，S2与S3关断，此时变换器输出电压E，负载电流上升；

状态2：开关S2与S3导通，S1与S4关断，此时变换器输出电压-E，负载电流下降；

状态3：开关S1与S2导通，S3与S4关断或开关S3与S4导通，S1与S2关断，此时变换器输出电压为0，负载电流通过开关管与二极管续流。

变换器在每一个控制周期中包含两种开关状态，以输出正电压，负载电流上升过程为例。其调制原理如图2(b)所示，图中：uT+、uT-为一组幅值与频率相同、相位相反的三角载波；uin为控制器输入的控制信号；ug1、ug4分别表示开关管S1与S4的驱动信号。

控制信号uin分别与两个三角波进行比较，当uin大于uT+时，ug1输出高电平、S1开通，当uin大于uT-时，ug4输出高电平、S4开通，反之S1、S4关断。根据图2(a)主电路结构以及图2(b)中的开关时序图，此时变换器包含状态1与状态3两种开关状态，对负载输出等效的正向PWM电压。将控制信号与载波信号做归一化处理，即uTmax=1、uTmin=-1、uin∈[-1, 1]、占空比d=|uin|，则可以推导出该H桥变换器的输出模型为：

uout=

(1)

式(1)描述了功率放大器的PWM调制及主电路部分的非线性模型，实际上由于功放系统的控制频率很高，由PWM调制引入的非线性对系统性能的影响较小，因此，在分析稳定性时可以用一个电压放大倍数KV进行等效。

1.2 定子线圈负载数学模型

电流控制回路中负载为磁悬浮轴承的定子线圈，使用叠片定子结构时，可以等效为阻感负载R、L串联的形式，其传递函数为

(2)

式中L=N2/R0，N为绕组匝数，R0为静态磁阻，分为气隙磁阻与铁心磁阻两部分，表达式为

(3)

式中：δ0为气隙长度；A为磁极面积；lm为铁心等效长度；μ0为真空磁导率；μr为铁心的相对磁导率。

采用实心定子结构时，磁路中的涡流效应不能忽略，铁心部分磁阻将随频率发生变化，根据文献[19]中的推导，此时磁阻可以表示为静态磁阻R0与动态磁阻Rt之和的形式，其中动态磁阻表达式为

(4)

将式(3)、式(4)代入式(2)，得到涡流效应影响下磁悬浮定子线圈的数学模型为

(5)

两种负载的频率特性如图3所示。可以看出，相比于叠片结构(整数阶负载)，实心结构(分数阶负载)在幅频特性上表现出更低的转折频率，其中高频段的衰减较大；而在相频特性方面，其相位在低、中频段滞后更为严重。

1.3 控制器数学模型

磁悬浮电流环控制器常采用PI(比例-积分)的形式，对于线性负载，该控制器完全可以达到较好的控制效果，其形式为

(6)

式中KP、KI为控制器的比例和积分系数，KP可以提高电流的响应速度，KI用来消除静态误差。对于数字控制系统，必须考虑由数字控制引入的延时，结合功率放大器的调制原理，延时通常为1.5个开关周期[20]，因此在传递函数中需要加入e-1.5Ts的延时环节。

输出电流由互感器检测并转换为电压信号用于反馈控制，该环节用增益KS来表示，通常情况下传感器及其检测电路带有低通滤波器，可以由一个一阶惯性环节来描述，表达式为

(7)

式中Ti为惯性环节的时间常数。

2 电流环控制系统稳定性分析

功放电路环的主要参数如表1所示，根据图1所示闭环控制系统，代入表1中的参数，研究两种负载情况下磁悬浮励磁电流控制系统的稳定性。

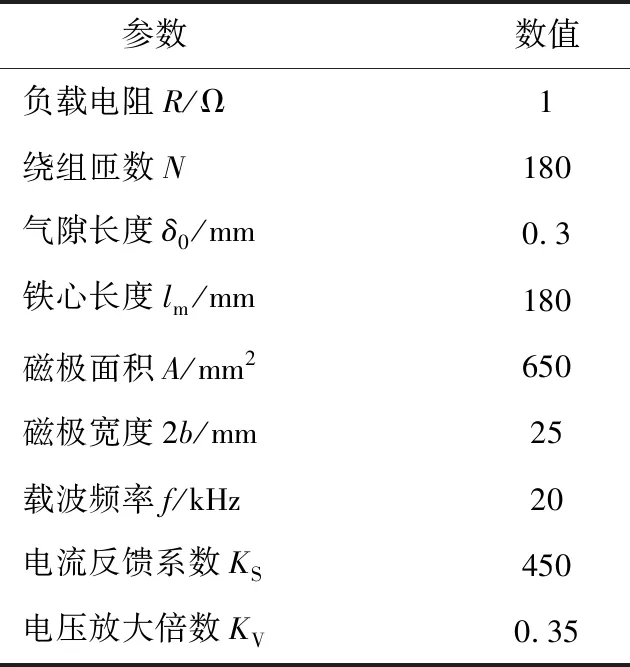
表1 功放电路环的主要参数

首先，叠片定子结构(整数阶负载)时，电流环控制系统闭环传递函数的特征方程为

1+KVC(s)G1(s)H(s)=0。

(8)

以KP为变量求解出考虑延时环节及不考虑延时环节的根轨迹曲线如图4所示，图中KP的变化范围为0.1～5。可以看出，若不考虑控制延时，整数阶系统在整个比例系数的调节范围内都稳定，而考虑延时环节后，系统有一对特征根在KP>2.65后跨越至正半平面，可知系统在KP∈[0.1, 2.65]范围内保持稳定。

在参数不变的情况下，代入实心定子(分数阶负载)的数学模型式(5)重新计算闭环系统根轨迹，结果如图5所示。根据分数阶系统稳定性判据定理，系统稳定的充要条件为

(9)

式中α为所含分数阶的阶数，即对于式(5)所示分数阶系统，每个特征根相角的绝对值大于45°，则系统稳定，如图5所示。可以看出，若不考虑延时环节，系统在整个KP变化范围内始终稳定，而考虑延时环节后，当比例系数KP增大到0.75时，系统将失稳。对比整数阶负载控制系统，KP稳定的范围大幅减小。

3 控制器设计及仿真

磁悬浮定子采用实心结构并考虑涡流效应后，磁悬浮定子线圈负载由一阶惯性环节变为分数阶环节，系统的控制性能发生较大改变，文中以系统的相位裕度为优化目标对控制器参数进行设计。

根据图1所示励磁电流控制系统的结构，系统开环传递函数的频率形式为

GH(jω)=C(jω)G2(jω)H(jω)。

(10)

在此基础上给定系统相角裕度φm，并按以下条件对控制器参数进行整定：

1)控制系统开环传递函数截止频率ωc处的相角特性为

Arg[GH(jωc)]=-π+φm。

(11)

2)控制系统开环传递函数在ωc处的幅值特性为

|GH(jωc)|dB=0。

(12)

3)为保证系统对增益变化的鲁棒性，要求系统开环传递函数的相位在截止频率ωc附近是平坦的，即满足

(13)

结合以上优化条件，代入表1中的数据，设置相角裕度φm=45°，求解得到优化后PI控制器的参数KP=0.172 8、KI=730.170。将该控制参数代入系统，可得优化后控制系统的开环、闭环Bode图如图6所示。经计算，优化后控制系统的截止频率ωc=4 236 rad/s、相角裕度φm=44.99°、闭环系统的带宽为8 500 rad/s，性能满足磁悬浮控制系统要求。

为验证理论分析的正确性，在MATLAB/Simulink平台建立磁悬浮功率放大器的仿真模型，研究叠片结构(整数阶负载)与实心结构(分数阶负载)情况下磁悬浮励磁电流的响应情况。模型中功率放大器使用如式(1)所示的非线性模型，且设置了1.5个周期的控制延时。仿真得到电流阶跃响应波形如图7所示。

图7(a)为叠片结构(整数阶负载)时，不同比例系数控制下磁悬浮励磁电流的阶跃响应波形，可以看出，当KP=0.8时，控制系统性能良好。当KP上升到2.6时，电流的调节时间明显增大。而KP=2.8时，系统失稳，励磁电流产生自激振荡，且该比例系数与第2节中分析相符。图7(b)为实心结构(分数阶负载)时的电流波形，3条曲线分别对应KP=0.17、0.7、0.8。可以看出，当KP设置为0.17时，控制系统具有较好的动态性能，但随着比例系数的增大，电流波形逐渐变差，当KP=0.8时，系统发生自激振荡，同样与第2节中的理论分析一致。此外，当考虑分数阶负载时，系统稳定时的比例系数调节范围明显小于整数阶负载。

4 试验研究

为验证数学模型及理论分析的正确性，基于赛米控公司的IGBT模块SK25GH063建立磁悬浮功率放大器及电流控制系统如图8所示，并进行试验研究，以下试验波形均由示波器实采数据绘制。

图9为定子采用实心结构(分数阶负载)时，改变控制器比例系数得到的输出电流波形。可以看出，在该负载特性下，当比例系数KP=0.17时，输出电流能够很好地跟踪给定参考电流2 A，系统也具有较好的动态性能。当KP增大到0.6时，输出电流的超调量及调节时间明显变大，但最终趋于稳定。而当KP增大至0.7时，输出电流发生了高频振荡，其结果与理论计算值存在微小的偏差(理论计算的临界点为KP=0.75)，因为实际系统中不可避免地存在测量噪声等外界干扰。但是，该试验结果仍然较好地验证了理论分析的结论，使用实心铁磁材料时，比例系数增大，系统的稳定裕度降低，更进一步致使电流发生高频振荡。

根据前文的分析，采用叠片定子后，磁路中的涡流效应将大幅减小，负载变为一阶系统，具有更宽的比例系数调节范围。为验证结论，文中更换叠片定子重复上述试验，其电流响应波形如图10所示。可以看出，在同样的比例系数下，系统未出现失稳及自激振荡现象，与理论分析结果相同，但是同样可以看出，同样的比例系数下，电流的响应过程由欠阻尼变成了过阻尼，调节时间明显加大，可见使用叠片定子时需要配置较大的比例系数，否则动态性能将难以满足磁悬浮控制的需要。

根据理论分析，数字控制导致延时影响系统的稳定性是引发电流自激振荡的重要原因。因此，减小控制延时是增加系统稳定性的有效措施。试验利用模拟电路实现了PI控制及载波比较的功能，在实心定子(分数阶负载)上进行试验，结果如图11所示，可以看出，在比例系数0.6～1.0范围内，系统稳定，未出现振荡现象，且电流响应速度较快，系统具有较好的动态性能。

5 结 论

本文研究了涡流效应对磁悬浮轴承功率放大器性能的影响。文中详细对比了实心及叠片两种定子结构，分别建立负载的数学模型，考虑控制系统的延时，研究磁悬浮励磁电流控制系统的稳定性及动态性能，并通过仿真与试验对提出的理论进行验证，可以得到以下结论：

1)实心定子结构的磁悬浮轴承由于涡流效应的影响，其电磁线圈的负载特性表现为分数阶的形式，相比叠片的结构(整数阶负载)，其幅频特性表现出更低的转折频率和较小的下降斜率。

2)与叠片结构相比，实心定子的结构(分数阶负载)对于励磁电流控制系统的稳定性有负面的影响，其控制器比例系数的调节范围更小，且励磁电流更容易发生自激振荡。

3)对于实心和叠片两种结构，由数字控制导致的延时对励磁电流控制系统的稳定性有较大的负面影响，减小该延时能够较大地提高系统的稳定性。

文中的研究工作存在一定的不足，主要表现在：

1)本文建立负载线圈的分数阶模型时，假定所有的磁路都为实心铁磁材料，而实际的对象只有定子部分使用了实心结构，转子部分的磁路仍然是叠片结构，导致被控对象的理论模型与实际存在误差。

2)在分析根轨迹时，虽然考虑了数控系统的延时，但是变换器部分使用了线性模型，与实际的开关功放存在一定的误差。

3)试验中存在大量的外界干扰，如开关功放的电磁噪声、ADC转换引入的采样噪声等，这些未知的噪声将会对控制系统产生激励，造成稳定性的下降。

综上所述，理论模型的简化以及外部噪声使得理论分析与试验结果存在一定误差，在后续的研究中需要建立更加精确的模型并考虑噪声的影响。