问题与征解
2022-11-17
问题
问题19(供题者: 复旦大学 张奇) 甲与乙下棋获胜的概率是40%,但甲想不停地与乙下棋直到净胜乙五局就结束,他有可能做到这一点吗?如果有可能,请给出做到这一点的概率是多少;如果不可能,请说明原因.
注:读者在提供问题解答时,请先提供印刷体的版本,并注明单位、姓名和身份(教师、本科生或研究生等). 解答被选用后需提供word版本.
问题20(供题者:吉林大学 周鸣君) 设B是n(n≥1)中的单位开球,非负函数u在B内二阶连续可导,u(0)=0且u在B内不恒为0.试证明:对于任意的α>0,都存在ξ∈B, 使得Δu(ξ)>αu(ξ),其中
解答
问题10(供题者: 湖南交通工程学院高科技研究院 冯良贵) 设R={1,0,-1},Rn×n为R上n阶方阵全体, 证明:集合S={detA|A∈Rn×n} 必包含开区间(-2n-1,2n-1) 内的一切整数.进一步,提出如下开放问题:S是否就由闭区间 [-2n-1,2n-1] 内的一切整数所构成?
解以下解答由陈树人(武汉理工大学本科生,E-mail:1340511818@qq.com)和张神星(合肥工业大学副研究员,E-mail: zhangshenxing@hfut.edu.cn )独立给出.两份解答方法基本一致.前半部分选取了陈树人的解答,后半部分选取了张神星的解答.
构造矩阵A的行列式如下
第i行乘以-1加到第i+1行(i依次从n-2到 1),可得
再将第j列乘2加到第j-1列(j依次从n-1到 2),可得
显然(-2n-1,2n-1)中的整数可以用二进制展开表示为a1+2a2+...+2n-2an-1,其中a1,...,an-1取值为{-1,0,1},所以集合S必包含开区间(-2n-1,2n-1).


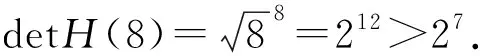
供题者点评作者利用整数的二进制表示, 结合行列式的基本性质成功地回答了此问题的第一部分.对此问题的第二部分,作者通过举例给出了否定的答案,并与著名的Hadamard猜想相联系,回答简洁有趣,恰好反映了问题提供者初衷.综上,解答人给出了该问题的一个完美回答.
