求一类不定方程x2+y2=zm的正整数解
2022-11-17戴中林
戴中林
(西华师范大学数学与信息学院,四川南充 637002)
1 引 言
对于不定方程xn+yn=zn的求解问题. 法国数学家费马(Fermat)早在1673年就给出了费马大定理[1]“当n≥3时,xn+yn=zn没有正整数解. ” 此后数学家们又对同类型的方程xn+yn=zm进行了探索和研究,并得出“若(m,n)=1,方程xn+yn=zm必有正整数解[2-5].”至于更特殊的不定方程x2+y2=z2,则有下面众所周知的勾股数原理.
引理若a,b为正整数,则方程x2+y2=z2的全部正整数解为(2ab,a2-b2,a2+b2).
而对于一类不定方程
x2+y2=zm(m为正整数),
(1)
其中的正整数m,根据算术基本定理,“任一大于1的自然数可分解为有限个素数之积.”由于最小的素数是2,大于2的素数均为奇数,而各奇数的幂或乘积仍为奇数,不妨设此奇数为p,则任意正整数m的分解式可记为m=p·2k(p为奇数,k=0,1,…,n),故对不定方程(1)的研究可归结于以下两种情形的不定方程的求解问题.
(i) 当p=1时,求解不定方程x2+y2=z2n.对于此类不定方程,其解法是应用勾股数原理可得求正整数解的迭代计算法. 即首先导出该方程的迭代计算公式,然后将迭代公式中的最后一组变量赋予满足一定条件的初始值代入,并依次计算出前一组变量的值,从而求得满足该方程的一组正整数解.
(ii) 当p为奇数时,求解不定方程x2+y2=zp·2n.对于这种类型的不定方程,其解法是首先将原方程改写为x2+y2=(zp)2n,并求出满足不定方程x2+y2=zp(p为奇数)的任一组正整数解,然后将此解作为初始值,再应用迭代法计算n次即求得原方程的正整数解.
2 主要结果及证明
2.1 关于不定方程x2+y2=zm解的概念
定义1[2]设不定方程x2+y2=zm的一组正整数解为(x,y,z).若x,y,z中有一个为零时,称这样的解(x,y,z)为方程的平凡解;若x,y,z均不为零,称这样的解(x,y,z)为方程的非平凡解.
对于平凡解,其求法简单故一般不予研究,而主要研究的是求不定方程的非平凡解.
定义2设不定方程为x2+y2=zm.
(i) 若一组正整数(x,y,z)满足方程,且x与y互素,则称解(x,y,z)为该方程的一组基本解[2];
(ii) 若一组正整数(λx,λy,λz)满足方程,而(x,y,z)不满足该方程,则称解(λx,λy,λz)为该方程的一组基本解.
例如,不定方程x2+y2=z3,容易得到正整数解(2,11,5),(2,2,2),(5,10,5).由定义2知,这三组解都是该方程的基本解.
定义3设不定方程x2+y2=zm的任一组基本解为(x,y,z),则解(xtm,ytm,zt2)与基本解(x,y,z)均为同类的解,简称同类解.
如上例中方程x2+y2=z3的三组基本解为(2,11,5),(2,2,2),(5,10,5).则其同类解应分别为(2t3,11t3,5t2),(2t3,2t3,2t2),(5t3,10t3,5t2).
2.2 求不定方程x2+y2=z2n正整数解的迭代计算法
定理1不定方程
x2+y2=z2n
(2)
有正整数解的充要条件是

证必要性.方程(2)即x2+y2=(z2n-1)2,由引理,存在正整数a1,b1,使得上述方程有正整数解
又由方程
再由引理,存在正整数a2,b2,使得方程有正整数解
依此类推,最后有方程
由引理,存在正整数an,bn,使得方程有正整数解
将上述一系列过程中的ak,bk(k=n,n-1,…,1)逐次代入, 并设
故得不定方程(2)的正整数解
充分性. 应用数学归纳法证明.

当n=k时,设解(x,y,z)满足方程x2+y2=z2k.
当n=k+1时,其解(X,Y,Z)应由n=k时的解(x,y,z)按迭代公式再计算一次,有
(X,Y,Z)=(2xy,x2-y2,x2+y2),
则
即当n=k+1时, 解(X,Y,Z)使得方程(2)成立,故对一切n,解(x,y,z)均满足不定方程(2).
将前证明中的各方程组按逆向顺序列出可得迭代计算法,其计算过程如下:

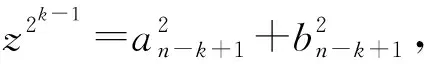
证应用数学归纳法证明.

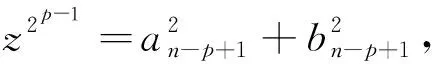
故当k=p+1时, 则由迭代公式
故有
即得

开方取正值即得

例如,对于不同的方程x2+y2=z2k(k=1,2,3),当取an=2,bn=3时,
其每组解中均为z=13.
由此得到求解不定方程(2)的迭代计算法:任意取定正整数an,bn为初始值,代入迭代公式中进行逐次计算,即可得到方程(2)的一组正整数解(x,y,z).
2.3 不定方程x2+y2=zp·2n(p为奇数)的解法
若求不定方程
x2+y2=zp·2n
(3)
的正整数解(x,y,z),应首先求得不定方程
x2+y2=zp
(4)
的任一组正整数解(x0,y0,z0),然后将其作为初始值应用n次迭代法,其计算过程为
即得不定方程(3)的一组正整数解(x,y,z).
3 应用实例
例1求不定方程x2+y2=z8的最小基本解及其同类解.
解应用定理1的迭代计算法,本例方程中n=3,应计算三次,为求该方程的最小解,可取初始值a3,b3为最小值,且(a3,b3)=1,故取a3=2,b3=1,则有
即得最小基本解(336,527,5)及其同类解(336t4,527t4,5t).
例2不定方程x2+y2=z12的最小基本解及其同类解.
解由文中第二种情形的方法,应先求x2+y2=z3较小的基本解. 应用观察法可求得三组较小的基本解(2,2,2),(2,11,5),(5,10,5),显然只有解(2,11,5)是方程x2+y2=z3的最小基本解,故可将其作为初始值,再应用迭代法再计算2次.
即求得原不定方程的最小基本解(10296,11753,5)及其同类解(10296t6,11753t6,5t).
需要说明的是,解(2,2,2)虽然是该方程的最小解,但不是原方程的基本解.事实上,由迭代法解得
即原方程的解(0,64,2)为平凡解,故(2,2,2)不是原方程的一组基本解.
例3求不定方程x2+y2=z30的最小基本解.
解该例属于引言中第二种情形,分两步进行计算.
第一步,应首先求出不定方程
x2+y2=z15
(5)
的一组最小基本解.
不妨设方程(5)的某一组正整数解[2]为
x=arct,y=brct,z=cs.
(6)
代入方程(5)得
a2r+b2r=c15s-2t.
(7)
欲求方程(5)一组最小基本解,其方法是以下各值均应取最小正整数.
(i) 取方程(7)右端c15s-2t为最小值c,即得不定方程15s-2t=1,可求得一组最小正整数解s=1,t=7;
(ii) 由a2r+b2r=c,取最小正整数r=1,a=1,b=2,即得最小正整数c=5;
(iii) 将上述各值代入解(6)中,即得方程(5)的最小基本解(57,2·57,5).
第二步,然后再以正整数解(57,2·57,5)为初始值应用迭代法一次, 即得原不定方程的最小基本解(4·514,3·514,5).
4 结 论
本文对不定方程x2+y2=zm有解的情形进行系统的研究. 特别是当m=p·2n(p为奇数)时,将该方程化分为两类,一类是关于不定方程x2+y2=z2n的求解,给出了理想的解决方法即迭代计算法;另一类是关于不定方程x2+y2=(zp)2n(p为奇数)的求解,虽然该方程看是形式复杂,但其解法过程却非常完美而简单,从而解决了一类不定方程x2+y2=zm的求解问题.
致谢作者十分感谢相关文献对本文的启发以及审搞专家对本文提出的宝贵意见.
