关于矩阵的中心化子的刻画
2022-11-17任芳国和嘉琪周红军
任芳国, 和嘉琪, 周红军
(陕西师范大学数学与统计学院,西安 710119)
1 引 言
矩阵具有丰富的研究内容又是研究自然科学的重要数学工具.矩阵是高等(线性)代数教学中重要的内容[1],贯穿于教学的始终,矩阵的运算是矩阵理论的基础 ,矩阵的乘法一般不满足交换律,矩阵代数是有限维的非交换代数典型代表,因此讨论矩阵的可换性具有特殊的意义.本文主要在学习高等(线性)代数基础上,讨论矩阵可换的重要特性,随后给出矩阵中心化子C(A)的维数及C(A)与P(A)相等的充分必要条件.
定义1[1]设A,B∈m×m,如果有AB=BA,称矩阵A与B可换.
定义2设A∈m×m,B∈n×n,如果存在C∈m×n,使得AC=CB,称A与B有缠绕关系.
注 矩阵的可换性就是特殊的缠绕关系.
定义3[1]给定数λ0及正整数k,称形如
的上三角的k阶方阵为一个以λ0为主对角线元素的k阶Jordan块,记作Jk(λ0),以Jordan块为主对角线元素的分块对角矩阵称为Jordan矩阵.
定义4[1]设A∈n×n.n×n中和A可换的所有矩阵做成的集合称为A的中心化子,记作C(A),即C(A)={X∈n×n|AX=XA}; 将A的所有矩阵多项式做成的集合记为P(A),即
P(A)={f(A)|f(x)∈C[x]}.
注[6]显然P(A)⊆C(A).
定义5[1]设A∈n×n,称关于λ的多项式det(λIn-A)为A的特征多项式,记作pA(λ); 称以A为根的次数最低的首一多项式称为矩阵A的最小多项式,记作mA(λ).
定义6[1]设f(x)=xn+a1xn-1+…+an-1x+an,ai∈,i=1,…n,称n阶方阵
为多项式f(x)的友矩阵,记作Cf.
定义7[3]设A∈n×n.如果A的每个不同特征值的几何重数为1,称A是无损矩阵.
下面不加证明的罗列出高等(线性)代数已经学习的关于矩阵可换的基本结果作为引理.
引理1[1]设A,B∈n×n且A与B可换,则A与B有公共的特征向量.
引理2[1](Hamilton-Cayley定理) 矩阵A是它特征多项式pA(λ)=|λIn-A|的根,即pA(A)=0.
引理3[1]设A,B∈n×n.
(i) 矩阵A与所有n阶方阵可换当且仅当A是数量矩阵;
(ii) 矩阵A与所有n阶可逆矩阵可换当且仅当A是数量矩阵;
(iii) 如果A=diag(d1,…,dn),其中d1,…,dn互不相同,那么A与B可换当且仅当B是对角矩阵;
(v) 可换性具有相似不变性,即A与B可换当且仅当S-1AS与S-1BS可换,其中S∈n×n是可逆矩阵.
引理4[4](中国剩余定理) 设p1(x),…,pn(x)是数域F上两两互素的多项式,其次数分别为m1,…,mn,则对数域F上任意n个多项式f1(x),…,fn(x),存在唯一的次数小于m1+…+mn的多项式f(x),使得f(x)≡fi(x)mod(pi(x)),i=1,…,n.
2 重要结果
首先看可换矩阵特征值的性质.
定理1设A,B∈n×n且A与B可换,则存在可逆矩阵P∈n×n,使得P-1AP,P-1BP都是上三角矩阵.
证对n作数学归纳证明.结论对n=1显然成立; 假设结论对n-1成立,现在看n的情况.由引理1知,A与B有公共的特征向量,设为x1,并设Ax1=λ1x1,Bx1=μ1x1,将x1扩充为n的一组基x1,x2,…,xn,作n阶可逆矩阵P1=(x1,x2,…,xn),则
那么A1B1=B1A1,于是由归纳假设知存在n-1阶可逆矩阵V1,使
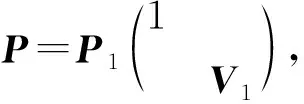
综上,定理得证.
推论1设A,B∈n×n.如果A与B可换,λ1,…,λn是A的特征值,μ1,…,μn是B的特征值,则
(i) A+B的特征值是λ1+μi1,…,λn+μin,其中i1,…,in是1,…,n的某个排列;
(ii) AB的特征值是λ1μi1,…,λnμin,其中i1,…,in是1,…,n的某个排列;
(iii) 若B是幂零矩阵,则A与A+B的特征值相同.
证由于A,B可换,由定理1知,存在可逆矩阵P∈n×n,使得
那么
再由相似矩阵有相同的特征值知,(i),(ii)成立;
(iii) 若B是幂零矩阵,则B的特征值为零,即μ1=…=μn=0,因而由(i)知,A与A+B的特征值相同.
注 如果A与B不可换,不一定存在可逆矩阵P,使得P-1AP与P-1BP是上三角矩阵.如
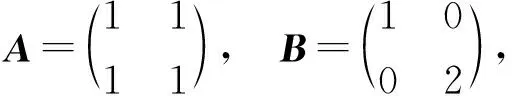
因为它们没有公共特征向量.
现在看矩阵缠绕关系的基本性质,并为后面讨论提供基础.
定理2设A∈m×m,B∈n×n.
(i) 如果A与B有缠绕关系,f(x)是任意多项式,那么f(A)与f(B)具有缠绕关系;
(ii) 如果A与B的特征值互不相同,那么矩阵方程AX-XB=O只有零解.
证(i) 由于A与B有缠绕关系,即存在C∈m×n,使得AC=CB,那么
A2C=A(AC)=A(CB)=(AC)B=(CB)B=CB2, A3C=A(A2C)=A(CB2)=(AC)B2=CB3,

即f(A)与f(B)具有缠绕关系.
(ii) 显然O是矩阵方程AX-XB=O的一个解.如果AX-XB=O有非零解X0∈m×n,即有AX0=X0B,那么由(i)知,对任意多项式f(x),有f(A)X0=X0f(B).特别地,pB(A)X0=X0pB(B),由引理2知,pB(B)=O,所以pB(A)X0=O; 设λ1,…,λn是B的特征值,有pB(x)=(x-λ1)…(x-λn),进而
pB(A)=(A-λ1Im)…(A-λnIm),
由于A与B的特征值互不相同,则每一个A-λiIm(i=1,…,n)可逆,那么pB(A)可逆,于是由pB(A)X0=O得X0=O,矛盾,故矩阵方程AX-XB=O只有零解.
推论2设X∈m×n,如果Jm(μ)X=XJn(λ) ,其中λ≠μ,那么X=O.
证由于Jordan块的特征值就是其对角线元素,则Jordan块Jm(μ),Jn(λ)的特征值互不相同,因此由定理2知,X=O.
推论3设A,B,C∈n×n,AB=CA,且
B=B1⊕…⊕Bk, C=C1⊕…⊕Ck
是分块对角矩阵,它们的分法完全相同.如果Bi,Cj的特征值互不相同,i≠j,那么A=A1⊕…⊕Ak是分块对角矩阵且AiBi=CiAi,i=1,…,k.
证对矩阵A进行分块,使得A的分法与B完全相同,设A=(Aij)k,由于AB=CA当且仅当AijBj=CiAij,i,j=1,…,k,再由Bi,Cj的特征值互不相同,且i≠j及定理2知,Aij=O,i≠j,因此A=A11⊕…⊕Akk,令Ai=Aii,i=1,…,k,有A=A1⊕…⊕Ak且AiBi=CiAi,i=1,…,k.
推论4设A,B∈n×n.如果存在可逆矩阵S,使得A=S(A1⊕…⊕Ak)S-1是分块对角矩阵,其中Aj∈Mnj(j=1,…,k)且Ai,Aj的特征值互不相同,i≠j,那么A与B可换当且仅当B=S(B1⊕…⊕Bk)S-1,其中Bj∈Mnj(j=1,…,k)且AiBi=BiAi,i=1,…,k.
证由可换具有相似不变性知,A与B可换当且仅当S-1AS与S-1BS可换,则由推论3知,S-1BS=B1⊕…⊕Bk且Bj∈Mnj(j=1,…,k),AiBi=BiAi,i=1,…,k,即
B=S(B1⊕…⊕Bk)S-1.
定理3设A∈n×n.
(i)P(A),C(A)都是n×n的子空间且P(A)中的元素可换;
(ii) dimP(A)=∂(mA(x)).
证(i) 显然零矩阵都在P(A),C(A)中,此外它们关于矩阵加法及数乘封闭,这是因为,∀f(x),g(x)∈C[x],∀k∈,显然f(x)+g(x),kf(x)∈C[x],则f(A)+g(A),kf(A)∈P(A),于是P(A)是n×n的子空间.同理,∀B,C∈C(A),∀k∈,显然B+C,kB∈C(A),则C(A)是n×n的子空间,又P(A)中的元素可换是显然的;
(ii) ∀f(x)∈C[x],设m=∂(mA(x)),由多项式带余除法知,存在唯一的多项式q(x),r(x),使得
f(x)=q(x)mA(x)+r(x),
其中r(x)=0或∂(r(x)) f(A)=q(A)mA(A)+r(A)=r(A), 因此f(A)可由I,A,…,Am-1线性表出.假设I,A,…,Am-1线性相关,则存在不全为零的数a0,a1,…,am-1,使得 a0I+a1A+…am-1Am-1=O, 令g(x)=a0+a1x+…am-1xm-1,则g(x)是以A为根且次数比m低的非零多项式,这与mA(x)是A的最小多项式矛盾,故I,A,…,Am-1线性无关,因此I,A,…,Am-1是P(A)的一组基,所以 dimP(A)=∂(mA(x)). 综上,定理得证. 注 一般地C(A)中的元素不一定可换.如若A是数量矩阵,则C(A)=n×n. 下面讨论P(A)=C(A)的充分条件. 定理4[7]设A∈n×n,pA(x),mA(x)分别是矩阵A的特征多项式与最小多项式. (i) 如果A有n个不同特征值,那么P(A)=C(A); (ii) 如果A=Jn(0),那么 (iii) 如果A=Jn(λ0),那么P(A)=C(A); (iv) 如果A是无损矩阵,那么P(A)=C(A). 证(i) 设λ1,λ2,…,λn是A的n个不同的特征值,则A可对角化,即存在可逆矩阵S,使得 S-1AS=diag(λ1,λ2,…,λn); ∀B∈C(A),由于S-1AS与S-1BS可换,那么S-1BS就是对角矩阵,即 S-1BS=diag(b1,b2,…,bn), 再由于λ1,λ2,…,λn互不相同,则由拉格朗日插值多项式基本定理知,存在次数不超过n-1次的多项式φ(x),使得φ(λi)=bi,i=1,…,n,即 S-1BS=diag(φ(λ1),φ(λ2),…,φ(λn))=φ(S-1AS)=S-1φ(A)S, 因而B=φ(A)∈P(A),则再由B的任意性知,C(A)⊆P(A),则C(A)=P(A). (ii) ∀B=(bij)n∈C(A),即Jn(0)B=BJn(0),那么有 由此可得 ① 当i>j时,bij=0,即B是上三角矩阵; ②b11=bii,i=1,…,n,b12=b23=…=bn-1,n,…,b1,n-1=b2n,所以 令b1=b11,b2=b12,…,bn=b1n,再由Jn(0)的性质知 于是由B的任意性知,C(A)⊆P(A),所以C(A)=P(A). (iii) ∀B=(bij)n∈C(A),即Jn(λ0)B=BJn(λ0),而 Jn(λ0)B=BJn(λ0) ⟺ (λ0In+Jn(0))B=B(λ0In+Jn(0)) ⟺Jn(0)B=BJn(0), 于是由(ii)知,存在数a1,a2,…,an,使得 B=a1In+a2Jn(0)+…+anJn(0)n-1, 则 B=a1In+a2(Jn(λ0)-λ0In)+…+an(Jn(λ0)-λ0In)n-1∈P(Jn(λ0))=P(A), 再由B的任意性知,C(A)⊆P(A),所以C(A)=P(A). 使得S-1BS的分法与J的分法完全相同,即Bii与Jni(λi)同阶,于是由J与S-1BS可换可得, Jni(λi)Bij=BijJnj(λj),i,j=1,…,k, 当i≠j时,由于λ1,λ2,…,λk互不相同及推论2知,Bij=O,i≠j,即S-1BS是分块对角矩阵 S-1BS=B11⊕…⊕Bkk, 其中Jni(λi)Bii=BiiJni(λi),i=1,…,k,由(iii)知,存在多项式gi(x), 有 Bii=gi(Jni(λi)),i=1,…,k; 又Jni(λi)的最小多项式为mi(x)=|xIni-Jni(λi)|=(x-λi)ni,故m1(x),…,mk(x)两两互素,根据中国剩余定理知,存在多项式f(x),使得f(x)≡gi(x)mod(mi(x)),于是 S-1BS=g1(Jn1(λ1))⊕…⊕gk(Jnk(λk))=f(Jn1(λ1))⊕…⊕f(Jnk(λk)) =f(Jn1(λ1)⊕…⊕Jnk(λk))=f(J)=f(S-1AS)=S-1f(A)S. 因而B=f(A)∈P(A),再由B的任意性知,C(A)⊆P(A),所以C(A)=P(A). 综上,定理得证. 推论5设A∈n×n,pA(x),mA(x)分别是矩阵A的特征多项式与最小多项式. (ii) 如果A的所有初等因子两两互素,那么P(A)=C(A); (iii) 如果pA(x)=mA(x),那么P(A)=C(A); (iv) 如果A是pA(x)的友矩阵CpA(x),那么P(A)=C(A). (ii) 由于A的全部初等因子两两互素,则A的同一个一次因式方幂只有一个,因而由矩阵的Jordan标准形与矩阵的初等因子之间的一一对应关系知,A的每个不同特征值只对应一个Jordan块,即A是无损矩阵,于是由定理4(iv)可知,P(A)=C(A). (iv) 由于友矩阵CpA(x)的最小多项式与特征多项式都是pA(x),则由(iii)知,P(A)=C(A). 最后给定n阶矩阵A,考察C(A)的维数及P(A)=C(A)的充分必要条件. 定理5设A∈m×m,B∈n×n.A的全部初等因子为(λ-λi)mi,其中的全部初等因子为(λ-μj)nj,其中则矩阵方程AX=XB的线性无关解的个数是其中dij表示(λ-λi)mi和(λ-μj)nj的最大公因式的次数. 证由于矩阵Jordan标准形中Jordan块与初等因子具有一一对应关系,则存在可逆矩阵S∈m×m及T∈n×n,使得 S-1AS=JA≡Jm1(λ1)⊕…⊕Jmp(λp),T-1BT=JB≡Jn1(μ1)⊕…⊕Jnq(μq). 因此 AX=XB⟺SJAS-1X=XTJBT-1⟺JA(S-1XT)=(S-1XT)JB, 令Y=S-1XT∈m×n,由于Y=S-1XT,∀X∈m×n是矩阵空间m×n上的同构映射,则只讨论方程JAY=YJB的线性无关解的个数即可. 将m×n的矩阵Y进行分块,使得Y的行的分法与分块对角矩阵JA的列的分法一致,Y的列的分法与分块对角矩阵JB的行的分法一致,记所得分块矩阵为Y=(Yij)p×q,其中Yij是mi×nj矩阵,则JAY=YJB等价于pq个方程,即 Jmi(λi)Yij=YijJnj(μj),i=1,…,p;j=1,…,q. ① 当λi≠μj时,则由推论2知,Yij=O,此时((λ-λi)mi,(λ-μj)nj)=1,即 ∂((λ-λi)mi,(λ-μj)nj)=0. ② 当λi=μj时,则 Jmi(λi)Yij=YijJnj(μj) ⟺Jmi(0)Yij=YijJnj(0), 此时记Yij=(yst)mi×nj,其中1≤s≤mi,1≤t≤nj, 于是 当mi=nj时, 此时((λ-λi)mi,(λ-μj)nj)=(λ-λi)mi; 当mi 此时((λ-λi)mi,(λ-μj)nj)=(λ-λi)mi; 当mi>nj时, 此时 ((λ-λi)mi,(λ-μj)nj)=(λ-μj)nj, 推论6设A∈n×n.A的全部初等因子为(λ-λi)ni,其中则 (ii) dimC(A)≥n; (iii)C(A)=P(A)当且仅当A的所有初等因子两两互素. 证(i) 由于矩阵Jordan标准形中Jordan块与初等因子具有一一对应关系,则存在可逆矩阵S∈n×n,使得 S-1AS=JA≡Jn1(λ1)⊕…⊕Jnp(λp). ∀X∈C(A),有 AX=XA⟺SJAS-1X=XSJAS-1⟺JA(S-1XS)=(S-1XS)JA, 由定理5知 其中dij表示(λ-λi)ni和(λ-λj)nj的最大公因式的次数; (ii) 由于dii=∂((λ-λi)ni,(λ-λi)ni)=∂((λ-λi)ni)=ni,i=1,…,p,那么 (iii) 由于dimP(A)=∂(mA(λ))≤∂(pA(λ))=n≤dimC(A),所以 C(A)=P(A)⟺dimC(A)=dimP(A)⟺dimC(A)=n=dimP(A) ⟺dimC(A)=∂(mA(λ))=∂(pA(λ))⟺mA(λ)=pA(λ)⟺A 的所有初等因子两两互素. 最后看一个例子. 例设A∈6×6,JA=J2(1)⊕J2(1)⊕J2(2),求 (i) dimC(A); (ii)C(JA)中元素的一般形式. 解(i) 由A的Jordan标准形知,A的初等因子为 d1(λ)=(λ-1)2,d2(λ)=(λ-1)2,d3(λ)=(λ-2)2, 并令 dij=∂(di(λ),dj(λ)),i,j=1,2,3, 则 dii=2,i=1,2,3,d12=2=d21,d31=d13=d23=d32=0, (ii) ∀Y∈C(JA),即JAY=YJA,对Y做分块矩阵,使得它的分法与JA的分法完全一样,即Y=(Yij)3×3,其中每个Yij是2×2矩阵,于是由JAY=YJA知 其中a,b,c,d,e,f,g,h,j,k是任意数,则C(JA)中元素的一般形式为 本文首先归纳了矩阵可换性的一些基本性质,并讨论了可换矩阵的一个重要特性,通过矩阵缠绕关系的基本性质研究了矩阵的中心化子和矩阵多项式的集合P(A)相等的充分条件,最后获得了中心化子C(A)的维数及C(A)与P(A)相等的充分必要条件,并通过一个例子使读者们进一步了解中心化子的性质.通过研究可交换矩阵,对于更深层次理解矩阵有着积极的意义. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.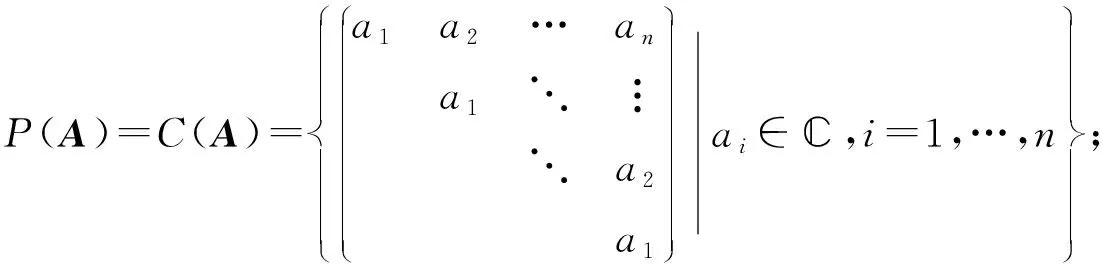


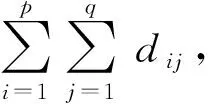
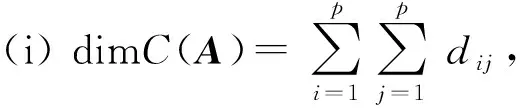
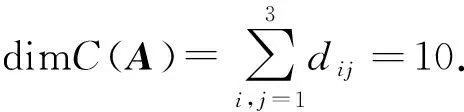

3 结 论
