一类数列极限的推广与应用
2022-11-17戴立辉黄建吾王宜洁
戴立辉, 黄建吾, 王宜洁
(闽江学院数学与数据科学学院,福州 350108)
1 引 言
《美国数学月刊》(The American Mathematical Monthly)2019年第4期的数学问题与解答刊登了这样一则数学问题[1]:
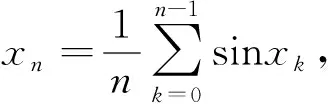
该问题的详细解答可见参考文献[1].本文拟对此问题中的数列构造作一般化处理,对该问题进行推广讨论,适用于更广泛的一类极限问题,得到如下定理.
2 一般形式
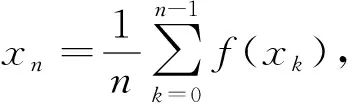
(1)

由此两式可得
(n+1)xn+1-nxn=f(xn),
(2)
或
(n+1)(xn+1-xn)=f(xn)-xn,
从而
(3)
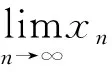
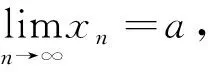
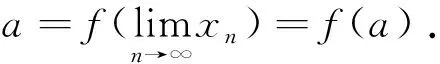
由题设知,当x→0时,f(x)=x-lx1+m+o(x1+m),故当n→∞时,
(4)
(5)
由式(2)得
上式两边令n→∞,则有
(6)
再次利用Stolz定理,有
利用式(3)和(4),当xn→0时,
从而

利用式(6),得到
(1)
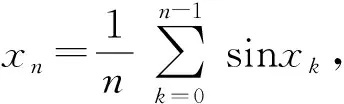
取f(x)=sinx,则当0 因此由式(1)知 下面进一步通过实例说明前述定理的应用. (7) 注 若对参数α,q赋予具体数值,可得很多相关数列的极限. (8) 令f(x)=ln(1+x)(x>0),容易证明0 故由前面已证的定理知 (9) 令f(x)=arctanx,不难证明0 故由前面已证的定理知 因此 (10) f(x)=x(1+xλ)-p=x(1-pxλ+o(xλ))=x-px1+λ+o(x1+λ), 故由前面已证的定理知 (11) 注 若对参数λ,p赋予具体数值,可得很多相关数列的极限. 故当x>0时,h(x)单调递增.又h(0)=0,所以h(x)>0,从而当x>0时,g′(x)>0,g(x)单调递增,而g(0)=0,所以g(x)>0,因此当x>0时,f(x) 故由前面已证的定理知 (12) 利用函数ex,e-x的幂级数展开式及幂级数的运算知,当x→0时 故由前面已证的定理知(取f(x)=tanhx) 证首先证明,当0 (13) 0 故由前面已证的定理知 (14) 证由sinx及arcsinx的幂级数展开式知 从而 故当0 arcsin(sin3x) (15) 令f(x)=x-arcsin(sin3x) (0 当x→0时,由于 (16) (17) 当x→0时,由tanx的幂级数展开式知 故由前面已证的定理知 因此 (18) 由于满足前述定理条件的数列有很多,故下面再列出几个供读者练习. 本文对已知命题的条件进行一般化处理,同时适当增加约束条件,适用于一大类型极限问题的研究.同时,定理的证明及应用仅涉及到高等数学常见的几个极限定理如单调有界定理、Stolz定理以及泰勒展开定理等,对教师高等教育教学研究或学生提升学习研究与创新实践水平都有较大的促进作用. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.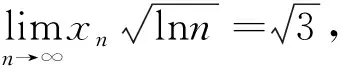
3 应 用
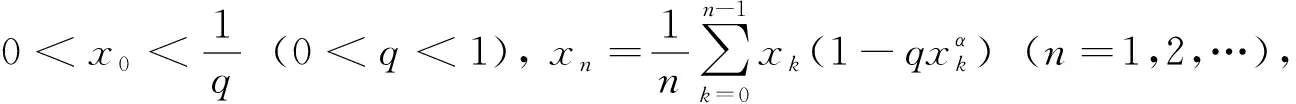
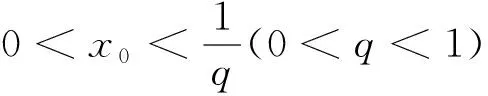
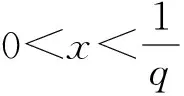
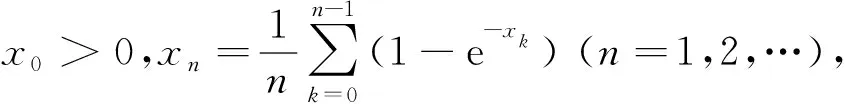


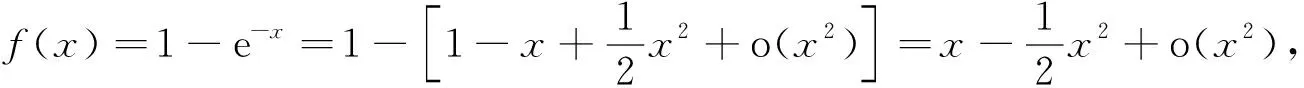
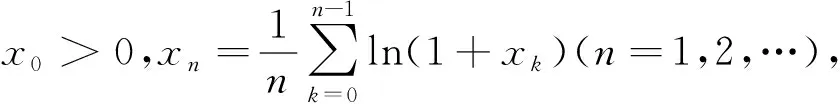


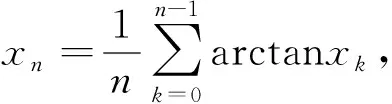

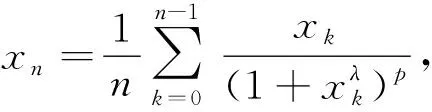
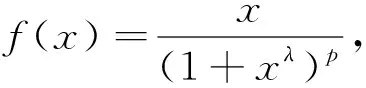

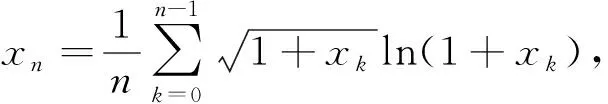

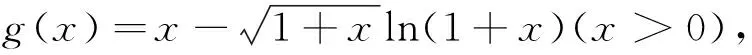
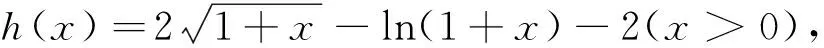

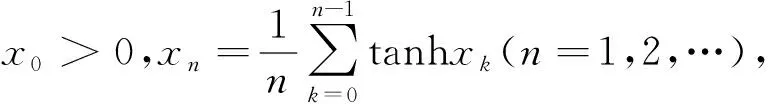
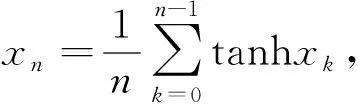
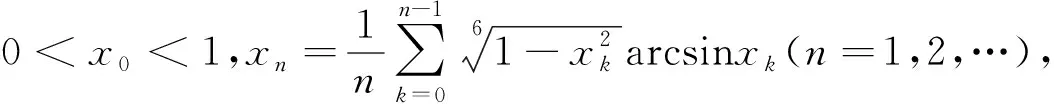
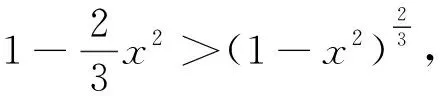
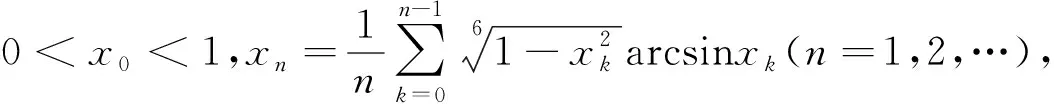
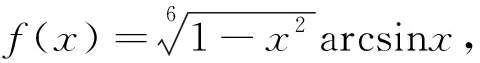
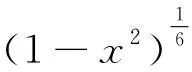
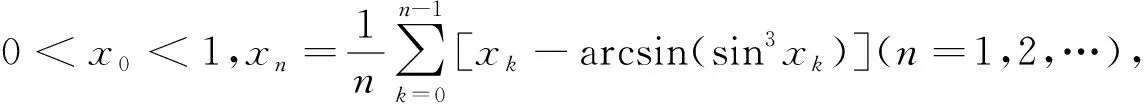
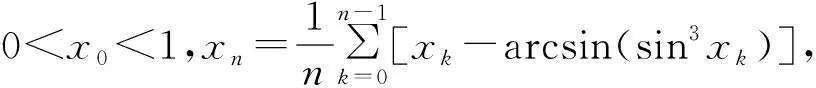
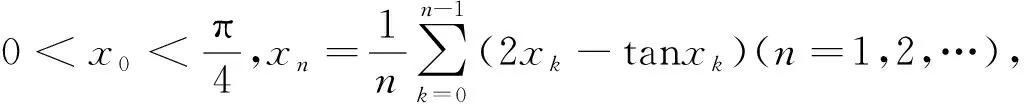

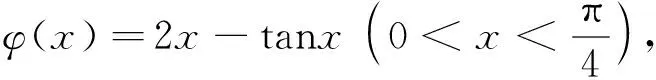
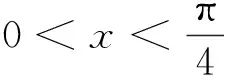

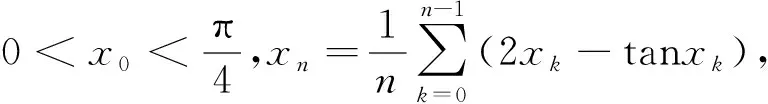

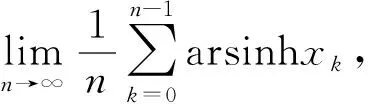
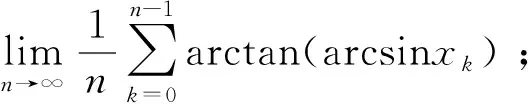
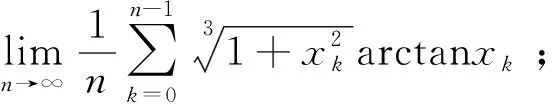
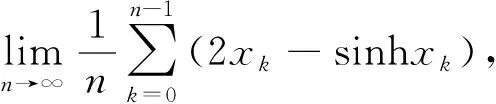
4 结 论
