内积空间矛盾方程组最小二乘解理论

郑素佩， 封建湖， 宋学力

(长安大学理学院，西安 710064)

1 引 言

线性矛盾方程组(下文如无特别说明，提到矛盾方程组均指线性矛盾方程组)在工程领域经常会遇到，比如房价预测、共享单车出租数量预测、空气污染情况预测等.对矛盾方程组数值求解方法的研究具有重要的理论意义与实际应用价值.关于矛盾方程组的最小二乘解，一般的思想是采用多元函数求极值的方法，寻找极值点以得到最小二乘解所满足的方程组，即法方程组[1-5].

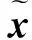
本文首先提出了一种“基函数”的恰当取值方法，并在内积空间理论框架下，推导出矛盾方程组最小二乘解所满足的法方程组，得到矛盾方程组系数矩阵列满秩是其最小二乘解存在且唯一的充分条件.通过证明得到两种理论框架(极值理论与内积理论)所得法方程组是等价的，最后通过两个算例展示用本文方法能非常方便地得到法方程组.

2 矛盾方程组最小二乘解理论

本节首先回顾采用极值理论推导矛盾方程组最小二乘解所满足法方程组的方法，然后提出基于内积理论的矛盾方程组最小二乘解理论，具体内容如下.

2.1 极值理论[1-6]

对线性方程组

(1)

若记

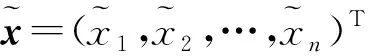
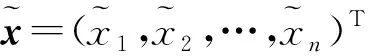
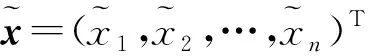
这一处理方式从知识体系角度来说没有同离散数据最小二乘曲线拟合问题解决方式统一起来，本文就这一问题进行研究，尝试在内积理论框架下将它们统一在一起.

2.2 内积空间中矛盾方程最小二乘解理论

本节给出如何将矛盾方程组最小二乘问题转化为基于“基函数”特定取值的离散数据最小二乘曲线拟合问题，推导出矛盾方程组最小二乘解内积形式的法方程组，给出法方程组解的存在、唯一性条件，以及两种理论框架所得结论的等价性关系等内容.

2.2.1 问题转化

通过“基函数”在离散点处的值取为矛盾方程组系数矩阵对应列处的值，实现将矛盾方程组最小二乘解问题转化为离散数据最小二乘曲线拟合问题.

现记“基函数”为φj(z)(j=1,2,…,n)，其在离散点zi(i=1,2,…,m)处的值取为方程组(1)系数矩阵A第i行第j列的值，即满足φj(zi)=aij(i=1,2,…,m;j=1,2,…,n)，详见下表1.

表1 基函数取值

令

该式右端当z=zi(i=1,2,…,m)时即为矛盾方程组(1)的左端.矛盾方程组(1)的最小二乘解问题可转化为使

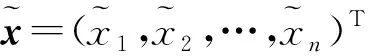
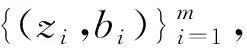
2.2.2 相关理论

由2.2.1节知可将矛盾方程组最小二乘解问题转化为对一组离散数据基于一组特定取值 “基函数”的最小二乘曲线拟合问题，本节将推导矛盾方程组最小二乘解在内积理论框架下的相关结论.

定义[4]在内积空间Φ中，对向量y=(y1,y2,…,ym)T∈m,z=(z1,z2,…,zm)T∈m，称

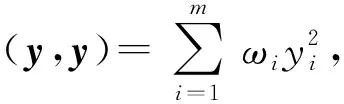
引理1[4]对向量y=(y1,y2,…,ym)T∈m，则‖y‖2=(y,y)1/2是一种向量范数，或有

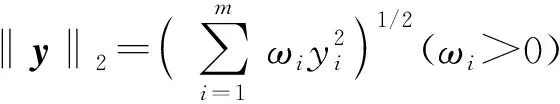
为讨论矛盾方程组最小二乘解的存在、唯一性，受文献[4]中证明技巧启发，给出如下引理.

(2)

为实对称半正定矩阵，其中内积

该反应遵循亲核消除机理，是可逆反应。与酯化反应相同，为使反应超正方向进行可加热脱水或使用甲苯等带水剂除去反应生成的水。

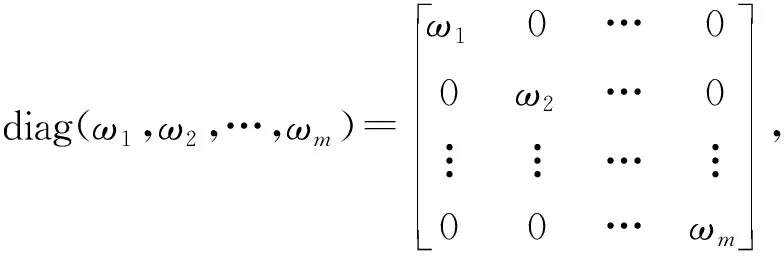
因ωk>0 (k=1,2,…,m)，则对任意0≠x=(x1,x2,…,xn)T∈n，有

xTGnx=xTATdiag(ω1,ω2,…,ωn)Ax=(Ax)Tdiag(ω1,ω2,…,ωn)Ax≥0.

故Gn为半正定矩阵，再由内积的性质知矩阵Gn为实对称半正定矩阵.

注 对线性矛盾方程组及离散数据最小二乘曲线拟合问题，离散Gram矩阵(2)均有引理所述性质.特殊地，对系数矩阵为列满秩矩阵的矛盾方程组(1)，所对应的离散Gram矩阵(2)为实对称正定矩阵.

证对矛盾方程组，由表1知

若A为列满秩矩阵，则有Ax≠0 (∀x≠0)，而ωk>0 (k=1,2,…,m)，由引理2知

xTGnx=xTATdiag(ω1,ω2,…,ωm)Ax=(Ax)Tdiag(ω1,ω2,…,ωm)Ax>0，

则此时离散Gram矩阵Gn为实对称正定矩阵.

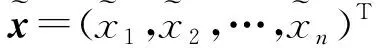
I(x)=(b,b)-2xTBn+xTGnx

基于2.2.1节的转化，现给出在内积空间中，矛盾方程组最小二乘解所满足的法方程组.

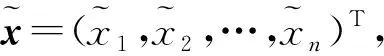
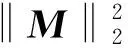
注1 为表述的严谨性，定理形式上很繁琐，而

和

注2 该定理将线性矛盾方程组最小二乘解问题统一在内积理论体系下.推导过程表明用该方法很容易得到一般性结论.

定理3在2.2.1节提出的将矛盾方程组最小二乘解问题转化为离散数据最小二乘曲线拟合问题的基础上，推导出矛盾方程组最小二乘解所满足的法方程组.那么用该方法推导得到的法方程组同采用极值理论得到的法方程组有什么关系呢？

定理4对线性矛盾方程组(1)的最小二乘解，采用极值理论得到的法方程组ATAx=ATb与基于内积理论得到的法方程组Gnx=Bn(详见定理3)是等价的.

证矛盾方程组最小二乘解问题，采用多元函数求极值的方法得到的法方程组为ATAx=ATb[1-6].取离散数据带权内积中权ω=(1,1,…,1)T，则

类似地可用矩阵乘法和内积公式得ATb=Bn.从而ω=(1,1,…,1)T时内积理论所得结论同极值理论所得结论等价.

在极值理论中取2-范数为带权ω=(ω1,ω2,…,ωm)T(ωi>0,i=1,2,…,m)型，离散数据内积也采用带同样权ω的内积，可以得两套理论所得法方程组依然是等价的.

3 例 题

本节通过两个简单的例子展示采用本文的方法非常容易得到线性矛盾方程组最小二乘解所对应的法方程组，且很容易判断出解的存在性.

例1解方程组

解该方程组的增广矩阵为

由表1的取值及离散Gram矩阵的表达式(2)知(权ω=(1,1)T)，法方程组系数矩阵和右端项为上面增广矩阵对应列向量的点积，易得法方程组(公式见定理3)，

解得x1≈2.9774127,x2≈1.2258727.

注 该例中线性方程组系数矩阵显然是列满秩矩阵，从理论上也很容易得出其最小二乘解存在且唯一(定理3结论).

例2[10]在开发一种抗过敏性的新药时，要对不同剂量的药效进行实验.10名患者各服用了该新药的一个特定的剂量.药物消失时立即记录.观测值列于下表2中.x是剂量,y是症状消除持续的日数.用7个不同的剂量，其中3个剂量重复给两名患者.试给出y与x之间的一元经验公式(保留3位有效数字).

表2 观测数据

解依据已知数据间的关系可将y与x之间的一元经验公式设为y=c0+c1x，易知常数c0,c1为如下线性矛盾方程组的最小二乘解

下面用本文方法求得法方程组，首先写出上面线性方程组的增广矩阵

再将增广矩阵的相应列向量求点积即得对应的法方程组(公式见定理3)

则y与x之间的一元经验公式为y=-1.07+2.74x.

该算例数据取自于文献[10]，通过该算例可以看出离散数据最小二乘曲线拟合问题是可以与线性矛盾方程组最小二乘解问题在一定条件下相互转化的，且用本文方法很容易得到法方程组.

4 结 论

本文给出了在内积空间理论下线性矛盾方程组最小二乘解理论，并推导了不同理论框架下所得结论的关系.极值理论所得线性矛盾方程组的法方程组与内积理论所得法方程组是等价的.在实际问题数值计算中，可以选用不同的权函数使所得结果更具实际意义.本文提出的算法能够很容易得到线性矛盾方程组所对应的法方程组且很容易讨论出线性矛盾方程组最小二乘解的存在、唯一性.所得结论仅适用于线性矛盾方程组最小二乘解问题，对非线性矛盾方程组的最小二乘解问题尚待进一步研究.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.