基于复值深度神经网络的目标检测方法

王佳琛 吴亿锋

（中山大学电子与通信工程学院，广东深圳 518107）

1 引言

雷达由于具有一定的穿透性、可全天候全天时探测感知等特点而被广泛应用于汽车、飞机等探测感知系统。雷达目标检测是指对雷达接收的回波信号进行处理后判断目标是否存在，是雷达系统最重要的功能之一。传统的雷达目标检测方法通常在对接收信号做匹配滤波、多普勒处理、波束形成等操作后，对结果进行假设检验以判断接收信号中是否存在目标回波。经典的恒虚警率（constant false alarm rate，CFAR）检测法使用奈曼-皮尔逊准则（Neyman-Pearson rule）进行目标检测［1］，该准则能在虚警率不超出可接受范围的前提下使得检测概率达到最大。假设检验通常由CFAR 检测器完成，其对每个待检测单元单独进行判决。由于回波信号中不仅存在可能的目标信号，还存在杂波、噪声、干扰等，这将导致传统雷达目标检测中出现一定的虚警、漏警。随着自动驾驶车辆、无人机等的发展，人们对目标检测的性能需求越来越高，例如自动驾驶车辆对道路行人的漏警可能导致严重的交通事故，因此雷达系统目标检测的不可靠性会严重约束雷达探测系统的应用发展。CFAR 经过多年的发展，为适应不同的环境，先后发展出了诸如单元平均恒虚警率、有序统计量恒虚警率、自适应恒虚警率和自由分布恒虚警率等方法［2］，这些方法均对场景模型具有一定要求，在实际处理过程中会因为模型不匹配、不准确等原因导致检测性能下降，因此我们亟须研究复杂场景下高效稳健的目标检测方法。

自2006 年学界提出深度学习的概念以来［3-4］，深度神经网络得到了极大的发展并取得了举世瞩目的成绩，其在语音识别、图像识别等领域不断刷新性能的上界［5］，已然成为炙手可热的研究对象，其中，卷积神经网络（convolutional neural networks，CNN）凭借优秀的表征学习能力和对图像平移不变特征的提取能力，在图像识别、姿态估计、行为认知等领域表现出良好的效果［6-7］。深度学习算法赋予了神经网络出色的拟合能力，使得其近年来在雷达领域颇有建树。文献［8］在认知雷达对微小无人机系统的探测和分类中使用了深度学习并取得了较好的效果。在［9］中，卷积神经网络被用以完成雷达波形识别任务。深度神经网络能够将数据映射到高维空间，从中提取目标信号、噪声等特征，因此亦被用于目标检测、合成孔径雷达目标识别、高分辨距离像目标识别等领域［10-14］。尽管深度学习在诸多领域成绩斐然，但目前绝大多数深度神经网络均基于实值操作与表示，鲜有问津复值深度神经网络。然而，［15］表明复值神经网络能更好地进行优化，HIROSE A.et al.在相关研究中发现复值神经网络拥有更好的泛化能力［16］，ARJOVSKY M.et al.在［17］中发现使用复数的神经网络能够拥有更丰富的表征能力。

本文开展了基于复值深度神经网络与多通道数据的目标检测方法研究，针对窄带雷达目标能量相对集中、具有一定空域相位关系等特点，提出了一种复值卷积神经网络（complex-valued convolutional neural networks，CV-CNN），该网络在传统目标检测的和通道-距离-多普勒域的更前端（即空域通道-距离-多普勒域）进行目标检测，利用深度学习带来的出色拟合能力在空域通道挖掘更多目标信息，特别是挖掘传统检测过程中损失的相位信息，根据目标回波在各空域（阵元域或子阵域）通道间不同于背景的相位关系实现了更高效的目标检测。本文为描述方便，下文统一将空域限定为阵元域。本文其他内容安排如下：第2 节介绍了信号模型，第3 节给出了基于复值深度神经网络的多通道目标检测方法，第4节通过实验验证了所提方法的有效性，第5 节对全文进行总结。

2 信号模型

考虑一个发射窄带信号的机载相控阵雷达系统，信号模型场景示意图如图1 所示，载机沿Y轴正方向以速度v平行于地面飞行，天线为N个阵元构成的均匀线阵，阵元间距为d，天线轴向与载机轴向的夹角为α，有一目标位于雷达侦测范围内，其相对于雷达的方位角、俯仰角分别为θ，φ。设一个相干处理间隔内有M个脉冲，对每个回波脉冲进行L个距离门的采样，则阵列接收的信号是一个N×M×L的阵元-脉冲-距离三维数据立方体X。

图1 信号模型场景示意图Fig.1 Diagram of signal model scene

假设目标位于第l个距离门，则该距离门处的目标回波可表示为：

式中sa0表示目标空域导向矢量，sb0表示目标时域导向矢量，二者可具体表示为：

其中fs=dcosθcosφ/λ=dcosψ/λ为目标的归一化空间频率，fd=2vcos(θ-α)cosφ/(λfr)为归一化多普勒频率，λ为信号波长，fr为脉冲重复频率表示矩阵转置。

第l个距离门的杂波回波信号可表示为：

式中Nc为当前距离门内杂波块的个数，sai与sbi分别为该距离门第i个散射块的空域导向矢量和时域导向矢量。

雷达接收到的干扰信号可表示为：

式中saJ与sbJ分别为干扰信号的空域导向矢量和时域导向矢量。

对任意一个距离门l(l=1，2，…，L)，根据是否含有目标信号，该距离门回波有两种假设形式：

其中Nl为噪声分量。L个距离门回波依次排列得到一个N×M×L的阵元-脉冲-距离三维数据立方体X，对一个回波数据立方体，在其脉冲域做傅里叶变换将其变换至多普勒域，此时回波数据变换为一个阵元-距离-多普勒复数据立方体，本文所提目标检测方法便是基于该复数据立方体进行的。

3 基于复值卷积神经网络的目标检测

传统雷达目标检测流程如图2 所示，雷达系统发射相干脉冲串并接收回波信号，回波信号经匹配滤波、多普勒处理、波束形成变换为和通道实数据，输入CFAR 检测器中进行目标检测。目标回波在阵元域存在一定的相位关系，而传统CFAR 检测方法仅在波束形成部分利用目标回波的相位关系对空域信息进行相参积累，没有充分利用目标回波的相位关系，性能有待进一步提升。

图2 传统雷达目标检测流程图处理Fig.2 Flow chart of traditional radar target detection method

目标检测是二元假设检验，亦可看作是二分类问题，因此可以将其视为自动目标识别的一种特例。由于深度神经网络拥有强大的分类能力，因此我们将深度神经网络代替传统CFAR 检测器进行目标检测；另一方面，为充分利用阵元域相位信息，我们设计了复值卷积神经网络对多通道复值雷达数据进行处理，从而通过复值卷积神经网络充分挖掘目标信号的多通道复值特征，提升目标检测性能。

3.1 基于复值卷积神经网络目标检测的整体流程

图3 给出了基于CV-CNN 的目标检测处理流程，含信号预处理和目标检测两个阶段。信号预处理阶段与常规目标检测预处理的前阶段比较类似，回波信号经匹配滤波、多普勒处理后变换为阵元-距离-多普勒复数据立方体，与传统信号处理流程不同的是所提方法未进行波束形成合成和通道，而是保留了多通道间的相位信息。目标检测阶段中，复数据立方体的距离-多普勒域被划分为若干等大区域，各区域对应的阵元-距离-多普勒数据块将输入CV-CNN 中进行分类，由分类结果判断数据块对应区域是否存在目标回波。值得注意的是，数据块距离-多普勒域的大小应略大于目标回波在距离-多普勒域上的大小，且数据块应包含对应区域的所有阵元信息，以便CV-CNN 利用阵元域相位信息检测目标。

图3 所提方法处理流程图Fig.3 Flow chart of target detection method

3.2 复值卷积神经网络设计

本文所提的复值卷积神经网络具体结构如图4所示，共有9 层，分别为2 层复值卷积层，3 层复值ReLU层，2层复值最大池化层和2层复值全连接层。卷积层、ReLU 和最大池化层为网络提供特征提取的能力，将输入数据的特征提取后送入全连接层中做出分类，以此判决输入数据中是否存在目标。

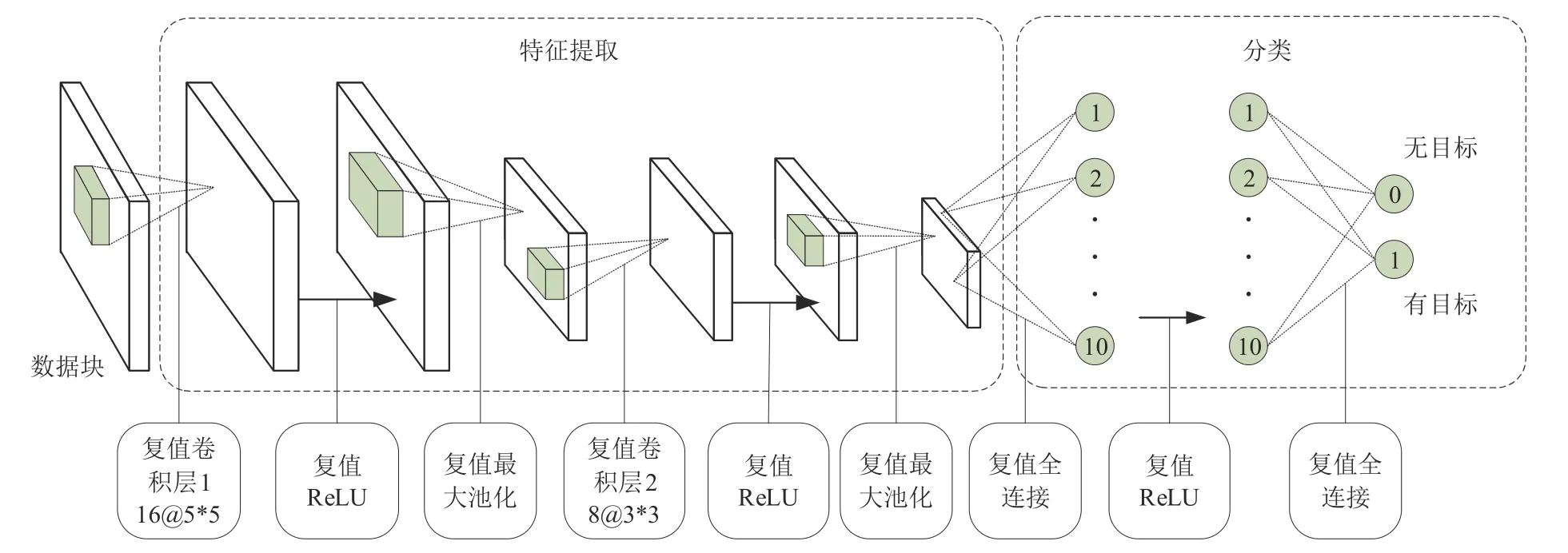
图4 CV-CNN结构Fig.4 Structure of CV-CNN

第一层复卷积层内的卷积层有16个卷积核，每个卷积核的尺寸为N× 5 × 5，第二层复卷积层内的卷积层有8 个卷积核，每个卷积核的尺寸为16 ×3 ×3，各卷积层步长均为1 且保持输入输出的宽与高不变。所有的复最大池化层内最大池化层的池化区域为3 × 3，步长为2，填充为1。第一层复全连接层有10 个输出，第二层则有2 个输出，分别对应有目标和无目标两种情况。

本文使用后向传播和随机梯度下降法对神经网络进行训练，用于训练神经网络的训练集由包含目标的数据块与不含目标的数据块构成，经过训练后的神经网络方能完成对上述两种数据块的分类任务。复值卷积神经网络的设计整体上包含神经网络的输入输出、复值卷积层、复值ReLU、复值最大池化层和复值全连接层［18］，接下来将逐一介绍。

3.2.1 网络输入输出

复值卷积神经网络的输入为包含了所有阵元的阵元-距离-多普勒三维数据块，输出为二元分类结果1 和0，输出为1 表示相应数据块包含目标，输出为0则表示数据块不含目标。

对于一个可能包含目标的复数据立方体，我们将其划分为若干数据块输入CV-CNN 中，通过输出结果判断数据块对应的区域内是否存在目标，进而完成目标检测。

3.2.2 复值卷积层

图5给出了复值卷积层的示意图。在实卷积层中，若W∈R 为卷积核，H∈R 为数据，则卷积结果可表示为W*H。因此结合复数运算规则，假设有复数卷积核W=A+iB∈C，数据H=C+iD∈C，其中A，B∈R 分别为实卷积核与虚卷积核，C，D∈R分别为数据的实部与虚部，则卷积结果为：

图5 复值卷积层示意图Fig.5 Diagram of complex-valued convolutional layer

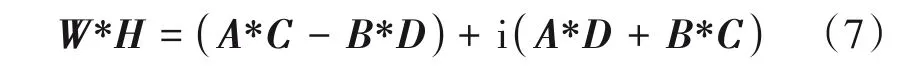
其中，(A*C-B*D)为卷积结果的实部，(A*D+B*C)为卷积结果的虚部。

3.2.3 复值ReLU

ReLU（Rectified Linear Unit）函数是深度学习领域较为常见的激活函数，主要作用于实数场景。本文针对复数场景，采用对数据的实部和虚部分别ReLU的方法作为复数场景下的ReLU函数。

3.2.4 复值最大池化层

复值最大池化层的实现方式如图6 所示，其实现原理与复值ReLU 相似，由两个实深度神经网络的最大池化层构成，数据的实部和虚部分别作为两个最大池化层的输入，各自的输出作为复值最大池化层输出结果的实部和虚部。

图6 复值最大池化层示意图Fig.6 Diagram of complex-valued maxpool layer

3.2.5 复值全连接层

在实深度神经网络中，全连接层的核心操作是矩阵向量积，即：

类比卷积层的实现方法，若输入数据为x=A+iB，则其矩阵权值应为W=W1+iW2，此时复值全连接层的矩阵向量积可表示为：

实现方法如图7所示。

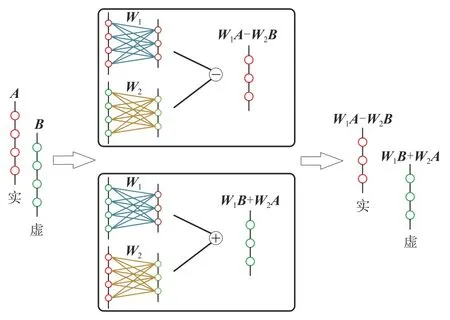
图7 复值全连接层示意图Fig.7 Diagram of complex-valued fully connected layer

4 仿真验证

为验证所提算法的性能，本节通过仿真实验比较CV-CNN 与单元平均CFAR（cell averaging CFAR，CA-CFAR）等检测器的检测性能，并给出其运行开销。本次仿真实验的数据模型参考了文献［19］，共仿真了无杂波和有杂波两种场景，其中有杂波情况下的杂噪比为10 dB，回波信号中包含了目标回波、噪声和杂波，而无杂波情况的回波信号中包含目标回波和噪声，并考虑了旁瓣欺骗干扰的有无。在仿真实验中，雷达天线有16 个阵元，相干处理间隔内包含64 个相干脉冲，每个脉冲均为线性调频波，载频1 GHz。复数据立方体在距离-多普勒域上划分的区域大小为32 × 8，即阵元-距离-多普勒三维数据块大小为16 × 32 × 8。

检测概率和虚警概率是衡量检测器性能的关键指标，本次仿真实验将在虚警概率相同的情况下比较CV-CNN 检测器和CFAR 检测器的检测概率，若某一检测器具有较高的检测概率，则认为该检测器性能较好。对于CFAR 检测器，我们设置了8 个距离参考单元、4个多普勒参考单元、20个距离保护单元和6个多普勒保护单元。我们将通过测试集获得CV-CNN 检测器的检测概率和虚警概率，由于CFAR 检测中的虚警概率与判决门限有明确的数学关系，因此我们可设置CFAR 检测器与CV-CNN 检测器虚警概率相同，从而根据检测概率比较两者的检测性能。

本次仿真实验仿真了阵元脉冲域信噪比从-21 dB到-17 dB 共计五种信噪比的情况。用于训练神经网络的训练集有两个，分别对应两种场景，其中无杂波场景对应的训练集中包含目标数据块、旁瓣欺骗干扰数据块和噪声数据块，有杂波场景对应的训练集则包含目标数据块和杂噪数据块。每个训练集由90000份数据块组成，各类数据块的数量相等，每种信噪比对应的数据块数量也相等。测试集与训练集的组成方式相同，每个测试集有2 × 105份数据块。训练集和测试集的数据均由仿真软件仿真得到。

接下来将分别对各个情况进行仿真，4.1 节仿真了无杂波情况，旨在说明所提方法在无杂波场景下对目标的检测能力和对旁瓣欺骗干扰的抑制能力，4.2节仿真了杂波情况，意图表明所提方法在杂波场景下对目标的检测能力，4.3 节给出了一种简单直接的复值神经网络，并通过仿真比较其与本文所提方法的检测性能，4.4 节给出了各目标检测方法的运算量运行开销。

4.1 无杂波场景下的仿真与分析

本小节首先仿真无旁瓣欺骗干扰信号的情况，比较了CV-CNN 检测器与CA-CFAR、广义似然比检验（generalized likelihood ratio test，GLRT）［20］的检测性能，其中GLRT 检测器在估计协方差矩阵时使用了与CV-CNN 检测器训练集相同规模的数据，即1.2 × 105个参考单元，并用该矩阵进行目标检测。随后引入旁瓣欺骗干扰信号，并同时引入旁瓣匿影，比较了CV-CNN 检测器与引入了旁瓣匿影的CA-CFAR 检测器的检测性能。接下来给出两种情况的仿真实验结果。

图8给出了无旁瓣欺骗干扰信号的仿真实验结果，在相同虚警概率0.01 的条件下，各检测器的检测概率由图中曲线给出，其中蓝色实线表示本文所提算法的检测概率，橙色虚线表示CA-CFAR检测概率，黄色实线表示GLRT 检测概率，从中可以看出，三种检测器在虚警概率相同的情况下，CV-CNN 检测器的检测概率在五种信噪比情况下均优于其他两种CFAR 检测器，且在低信噪比情况下优势明显，因此从实验结果来看，CV-CNN 检测器的性能要优于传统目标检测方法。

图8 检测器检测概率对比Fig.8 Comparison of probability of detection

图9给出了引入旁瓣欺骗干扰信号的仿真实验结果，其中干扰信号在距离-多普勒域的功率与目标信号一致，旁瓣匿影所用的辅助天线设为无方向性，且其增益较主天线第一旁瓣高3 dB，匿影门限设为0.6。图9 给出了两种检测器的目标检测概率Pd 与干扰虚警概率Pj 的仿真结果，其中Pd 指检测器检测到目标的概率，Pj 指检测器错误地将干扰检测为目标从而引起虚警的概率。图中蓝色实线和红色实线分别代表CV-CNN检测器的目标检测概率和干扰虚警概率，橙色虚线和黄色虚线分别表示CA-CFAR 检测器的目标检测概率和干扰虚警概率。从中可以看出，CV-CNN 检测器相比于CA-CFAR 检测器，其在干扰虚警概率较低的同时，能够拥有较高的目标检测概率，这意味着一个得到恰当训练的CV-CNN 检测器不但具备目标检测能力，还拥有抗旁瓣干扰的功能。

图9 CV-CNN检测器与CA-CFAR检测器性能对比Fig.9 Performance comparison with CV-CNN detector and CA-CFAR detector

4.2 杂波场景下的仿真与分析

本小节仿真了杂噪比10 dB 的情况，所选传统目标检测方法为最优STAP 与CA-CFAR 的组合，将其与CV-CNN 检测器进行比较，仿真实验结果如图10 所示，其中虚警率为0.013，图中蓝色实线表示CV-CNN 检测器的检测概率，橙色虚线表示最优STAP 与CA-CFAR 的检测概率。从中可以看出CVCNN 检测器在杂波环境下性能略好于传统目标检测方法。

图10 CV-CNN检测器与STAP检测器性能对比Fig.10 Performance comparison with CV-CNN detector and STAP detector

4.3 两种复值神经网络的仿真与分析

针对复值数据，一种简单直接的设计方法是将复值数据的实部和虚部分别输入实神经网络组成一个复值神经网络，本小节按照该设计方法，仿照第3 节中CV-CNN 的结构，给出了一种新的复值卷积神经网络RC-CNN，并将其与CV-CNN 进行比较，仿真结果如图11 和图12 所示，其中图11 为无杂波场景下的仿真结果，图12 为杂波场景下的仿真结果，图中蓝色实线表示CV-CNN检测器的检测概率，橙色虚线表示本节新提出的网络RC-CNN的检测概率，需要注意的是两种神经网络的虚警概率并不相同，无杂波和杂波场景下的CV-CNN 虚警概率分别为0.01 和0.013，而RC-CNN 的虚警概率则高达0.03 和0.032。从中可以看出，该网络能够完成目标检测任务，但由于其在一定程度上割裂了数据的实部和虚部，最终的性能表现并不理想。

图11 无杂波场景下两种网络的性能比较Fig.11 Performance comparison with two networks in clutter-free region

图12 杂波场景下两种网络的性能比较Fig.12 Performance comparison with two networks in clutter region

4.4 运行开销对比

运行开销是评价一个算法的重要部分，算法运行开销主要包括算法运行涉及的乘法次数和算法运行时间两方面，本小节将从这两方面比较本文所提方法与传统目标检测方法的运行开销。

乘法次数对比曲线如图13 所示，从图13 中可以看出，由于最优STAP 涉及矩阵求逆，GLRT 在求取检测统计量时涉及多次矩阵乘法，乘法次数较多，而神经网络的乘法次数为一固定值，CV-CNN 的乘法次数上升较为缓慢。

图13 乘法次数对比曲线Fig.13 Multiplication comparison curve

表1给出了各目标检测方法运行时间的统计结果，该结果是在5000 个快拍、16 个阵元和64 个相干脉冲的假设下得到的。从中可以看到，对于无杂波场景下的两种CFAR方法，GLRT方法的运行时间较长且检测性能较差，CA-CFAR 方法与CV-CNN 的运行时间较为接近，而后者在检测性能上是明显优于前者的；对于杂波场景，CV-CNN 在检测性能略优于最优STAP 方法的同时，在运行时间上有着显著的优势。

表1 目标检测方法运行时间对比Tab.1 Comparison of running time of target detection methods

5 结论

本文针对传统检测方法未能充分利用多阵元间的相位关系、性能有待进一步提升的问题，提出了一种利用阵元间相位关系的复值深度神经网络目标检测方法。与传统的和通道距离多普勒域的实数据检测不同，所提方法挖掘更原始的多通道复数域数据，利用复数卷积神经网络在阵元-距离-多普勒域实现了目标检测。实验结果表明，所提方法相较传统目标检测方法拥有更好的性能。下一步将考虑引入不平稳、非均匀杂波等复杂环境因素，探究所提方法在复杂环境下的性能表现，同时，针对宽带信号的目标检测方法也是下一步研究的方向之一。