基于二次否定剪切选择的入侵检测方法*

刘会会，牛 玲，孔韦韦

（1.周口师范学院，河南 周口 466001；2.西安邮电大学，西安 710121）

0 引言

计算机技术的迅猛发展极大地改变了人类的生产、生活模式，但随之而来的计算机安全问题也深深地困扰着广大用户。在此背景下，计算机信息安全已经成为国内外相关领域的研究热点，并产生了一系列技术模型和方法[1-3]。受生物免疫系统模型的启发，人工免疫系统模型得到了建立和发展，诞生了诸如克隆选择[4]、危险理论[5]、否定选择算法（Negative Selection Algorithm，NSA）[6-15]以及免疫网络[16]等多种模型，并被广泛用于计算机入侵检测领域。其中，NSA由于具有优良的自适应保护机制，被认为是目前解决入侵检测问题的重要方法。

NSA通过模拟T细胞成熟过程中的耐受机制，清除不能通过自体耐受的候选检测器，从而实现对非自体集合的识别以抵御计算机网络中的入侵行为。因此，理想的成熟检测器应该满足以下几点要求：1）能够尽可能地识别非自体集合；2）不能识别任何自体集合。

传统的NSA采用字符串形式对自体和检测器进行编码，虽然实现起来较为简单，但系统的整体检测率较低。Gonzalez[17]提出的实值否定选择算法（Real-valued NSA，RNSA）对传统NSA进行了较大改进，但由于检测器半径是固定值，因此，检测效率提升有限。为此，Zhou等提出一种新型否定选择算法（V-detector）[18-19]，该算法中的检测器半径可以根据自身与自体集间的距离自适应地进行调整，一定程度上提升了检测效率。文献[12]也对否定选择算法进行了较为全面的总结和阐述。不同于以往提出的否定选择算法，文献[13]首次提出了针对候选检测器进行两次否定选择过程，从而有效提升检测器生成效率，并尽可能减少了成熟检测器中的个体数量。然而，过分苛刻的耐受过程容易造成大量检测器被删除，从而在一定程度上将不可避免地对检测效率构成影响。

因此，本文将结合二次否定选择算法和文献[20]中的切割机制，提出一种基于二次否性剪切选择的入侵检测方法。该方法首先将新生成的检测器与成熟检测器集合作比对，清除能够被成熟检测器完全覆盖的个体以提升每个检测器的耐受性能；然后，将通过耐受性检测的检测器与训练自体集作比对，如果出现覆盖则对检测器进行剪切，并将剪切后的个体置入成熟检测器集合；最后，对成熟检测器集合进行优化，使用数量尽可能少、半径尽可能大的检测器覆盖尽可能大区域的非自体集合以提升整个入侵检测系统的综合性能。

1 经典实值否定选择算法

经典的RNSA模型主要分为半径固定型和半径可变型算法两大类。其中，前者通常以检测器的数量作为整个算法的最终迭代终止条件，假设随机生成一个候选检测器H，然后计算H与每一个自体训练集间的最小距离dis，如果dis＞dS+dH，则H可以作为成熟检测器集合中的元素。其中，dS和dH分别表示自体集合半径和候选检测器的半径。

在半径可变型算法中，常以非自体集合覆盖率作为整个算法的最终迭代终止条件，假设随机生成一个候选检测器H，然后计算H与每一个自体训练集间的最小距离dis，如果dis＞dS，则H可以作为成熟检测器集合中的元素，且其半径值为dis-dS。图1给出了两种类型算法的示意图。

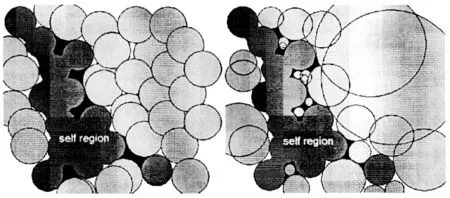
图1 半径固定型和半径可变型RNSA

其中，图中深灰色区域表示自体集合，淡灰色区域表示成熟检测器，自体集合之外的区域为非自体集合。在左图中采用了半径固定型检测器对非自体集合进行检测，而右图则采用了半径可变型的检测器对非自体集合进行检测。显然，半径可变型算法结果具有数量更少的成熟检测器以及检测率更高的检测效果。然而，这两种类型的算法均没有考虑候选检测器可能与成熟检测器之间的重叠覆盖。文献[13]针对此问题提出了二次否定选择算法，在原有RNSA基础上，添加了将候选检测器进行成熟检测器集合中元素耐受训练的过程，在一定程度上提升了检测器生成效率，但单纯一味地将与自体集合有重叠的候选检测器完全删除，容易造成检测效率的下降。

2 本文提出方法

本文结合二次否定选择算法和切割机制，提出一种基于二次否性剪切选择的入侵检测方法，该方法主要分为3个部分：成熟检测器耐受训练过程、训练自体集耐受训练过程、成熟检测器集合优化过程。

2.1 成熟检测器耐受训练过程

经典RNSA模型没有考虑候选检测器可能与成熟检测器之间的重叠覆盖可能。显然，一旦出现这种情况，将意味着新产生的候选检测器与现有的某个成熟检测器具有相似或者完全相同的覆盖范围和检测能力，因此，针对候选检测器进行成熟检测器集合的耐受训练是完全有必要的，有利于提高候选检测器的生成效率。

耐受训练过程具体步骤如下：

1）随机生成一个候选检测器H；

2）计算候选检测器H与成熟检测器中每一个个体之间的欧氏距离dis；

3）如果满足式（1），则候选检测器H通过了耐受训练；否则，返回步骤（a）；

其中dnew与di分别表示候选检测器与成熟检测器中第i个个体，rdi为成熟检测器di的半径，Nd为成熟检测器集合中的个体数量。

图2给出了候选检测器与成熟检测器间可能存在的3种位置关系示意图。

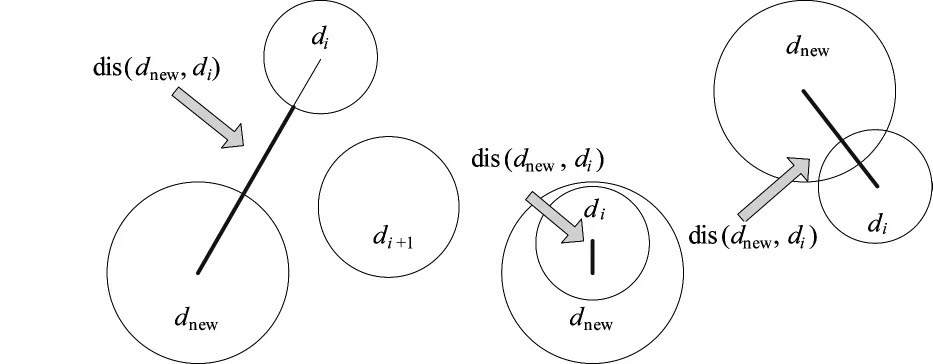
图2 候选检测器与成熟检测器间可能存在的3种位置关系

显然，当式（1）满足时，候选检测器与成熟检测器之间没有任何重复覆盖区域，因此，该候选检测器是必要的，并且不能被现有成熟检测器个体所取代；反之，如果式（1）得不到满足，则二者必然存在“部分相交”或“完全包含”位置关系，候选检测器的检测效能也将受到部分削弱或是完全覆盖。因此，任何一个合格的候选检测器必须满足式（1）。

2.2 训练自体集耐受训练过程

任何成熟检测器个体必须满足两个要素，即只能识别非自体集合且不能覆盖任何自体集合。因此，对任何候选检测器都有必要进行训练自体集的耐受训练过程。现有的绝大多数NSA模型对任何与自体集“相交”的候选检测器均采取“清除”策略，该策略实施简单，但容易造成大量候选检测器被删除从而影响检测效率。事实上，将这些检测器进行彻底“清除”是完全没有必要的，这些“瑕疵”检测器可以为我们提供自体集合与非自体集合间尤其是关于二者边界更多的位置信息，

本文借鉴文献[20]提出的剪切机制，对一些在训练自体集耐受训练过程中不合格的检测器进行切割，使之能够顺利通过耐受检验。

假设检测器类型为超立方体结构，训练自体集耐受训练过程具体步骤如下：

1）将通过检测器耐受过程的候选检测器H与训练自体集中的某个元素Straining作比对；

2）如果H与Straining有重叠区域，按照尺寸从大到小的顺序对H进行切割，生成4个新的检测器H1-H4，并将其列入候选检测器集合；否则，保持候选检测器H不变；

3）如果候选检测器与自体集合中所有元素均完成了耐受训练过程，算法结束，否则，返回步骤1）。

图3给出了二维空间情况下的候选检测器切割示意图。

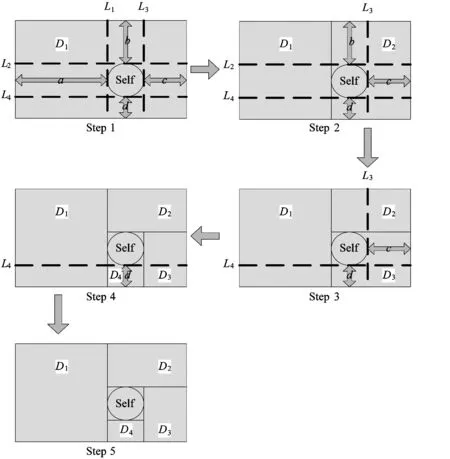
图3 二维空间下候选检测器切割示意图

在图3中，正方形区域表示候选检测器D1，中间圆形区域为训练自体集区域Self。显然，D1完全覆盖了Self，因此，必须对D1进行切割。从4个方向分别对D1到Self的空间位置进行测量，得出测量距离线长度为a＞b＞c＞d，对应的4条切割线均与这4条距离线垂直，分别为 L1，L2，L3，L4。为了尽可能保证大尺寸检测器形态的完整性，切割过程依次按照测量距离线由大至小的顺序进行。

Step 1中，沿切割线L1对原候选检测器D1进行切割，得到新生成熟检测器D1和右侧的“不合格”候选检测器D2；

Step 2中，沿切割线L2对原候选检测器D2进行切割，得到新生成熟检测器D2和下侧的“不合格”候选检测器D3；

Step 3中，沿切割线L3对原候选检测器D3进行切割，得到新生成熟检测器D3和左侧的“不合格”候选检测器D4；

Step 4中，沿切割线L4对原候选检测器D4进行切割，得到新生成熟检测器D4。

需要指出的是，虽然在图3中新生成的4个检测器在图3的示例中已经完全符合要求，但并不代表它们已成为成熟检测器，还需要与训练自体集中的其他元素分别进行比对完成耐受训练。

2.3 成熟检测器集合优化过程

经过成熟检测器耐受训练和训练自体集耐受训练后的检测器均为合格的检测器个体，理论上将全部归入成熟检测器集合，但由于不同成熟检测器间可能存在多种复杂的位置关系，如“包含”、“部分相交”等，因此，有必要对最终的成熟检测器集合进行优化，以期提高检测器的检测性能。图4为成熟检测器集合中检测器间可能存在的多种位置关系。

图4 成熟检测器间可能存在的位置关系

成熟检测器集合优化过程的具体步骤如下：

1）选取成熟检测器集合中的检测器Di作为基准检测器；

2）计算检测器Di与成熟检测器集合中其他检测器Dj（j≠i）间的距离dis（Di，Dj）；

3）若dis（Di，Dj）≤|RDi-RDj|，则检测器间存在“包含”情况，图5为检测器间存在“包含”情况的示意图，此时从成熟检测器集合中删除半径较小的检测器个体；否则，转向4）；其中，RDi与RDj分别表示基准检测器Di与其他检测器Dj的半径。

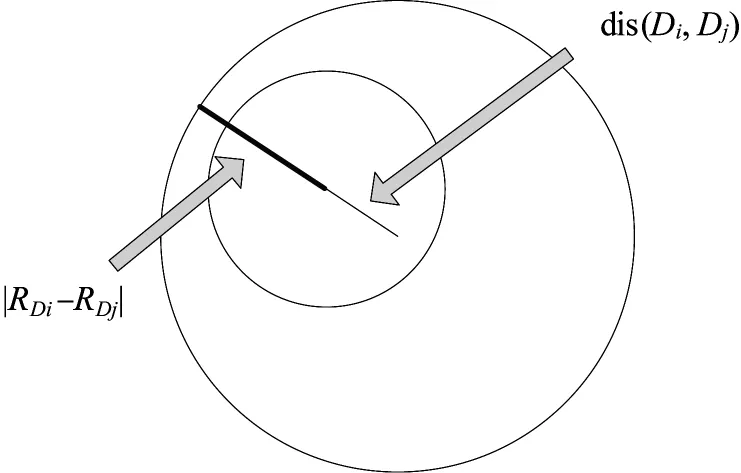
图5 成熟检测器间的“包含”关系

图6 成熟检测器间的“分离”关系

4）若dis（Di，Dj）＞|RDi-RDj|，则检测器间存在“分离”情况。图6为检测器间存在“分离”情况的示意图，以基准检测器Di与其他检测器Dj中心位置连线的中点作为圆心，以dis（Di，Dj）-（RDi+RDj）作为半径构建新检测器 D（new）k，删除检测器 Dj；特殊地，若dis（Di，Dj）-（RDi+RDj）＜rs[j]，则不构建新检测器 D（new）k，并保持检测器 Di，Dj不变；否则，转向 5）；

5）若|RDi-RDj|≤dis（Di，Dj）≤RDi+RDj，则检测器间存在“部分相交”情况，图7为检测器间存在“部分相交”情况的示意图；

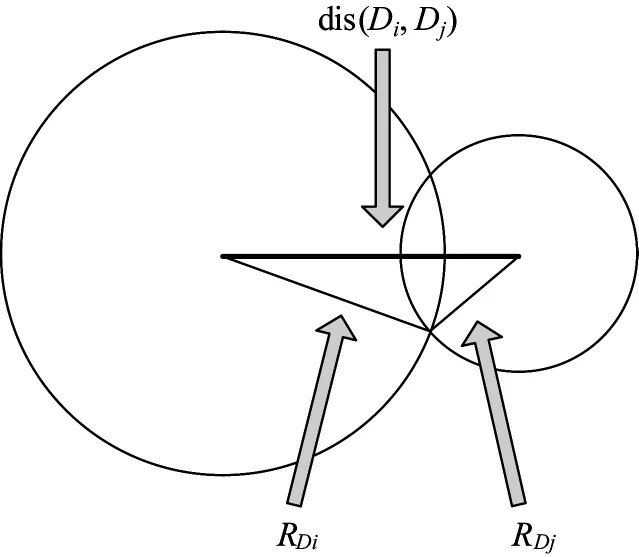
图7 成熟检测器间的“部分相交”关系

定义参数β，γ分别为图7中RDi与dis（Di，Dj）、RDj与dis（Di，Dj）间的夹角，即：

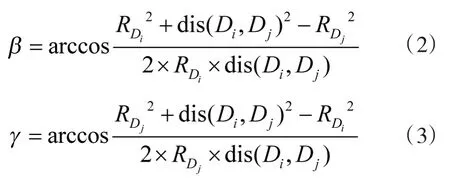
若 max（β，γ）≥π/3 且 β≥γ，则删除检测器 Di；若 max（β，γ）≥π/3 且 β＜γ，则删除检测器 Dj；否则，保持检测器 Di，Dj不变；

6）若成熟检测器中所有检测器均参与了讨论，算法结束；否则转向2）。

3 实验与分析

3.1 实验描述

本节将对文中所提方法的有效性进行仿真验证，仿真实验平台是一台PC，配置为2.3 GHz处理器、4 G内存以及VC++程序语言。简单起见，选取圆环形数据集作为训练自体集，且设定自体集半径为 0.05，各维特征均归一化至[0，1]n区间内，实验选取Iris标准数据作为测试对象。

为了进行比较，选取了经典RNSA、V-detector以及DNSA 3种方法与本文方法进行比较。其中，RNSA方法采用固定半径型检测器模型，这里设定为0.10，而另两种方法均采取可变半径型检测器模型，可以根据检测器中心与自体集中心间的距离自适应设定。本节将针对包括本文方法在内的4种方法进行3组仿真实验。

3.2 成熟检测器数量比较实验

在保证一定覆盖率的前提下，成熟检测器数量在一定程度上是衡量一种方法优劣的重要指标。方法所需的成熟检测器数量越少，方法的性能就越优越，表1给出了4种方法在成熟检测器数量指标上的比较结果。

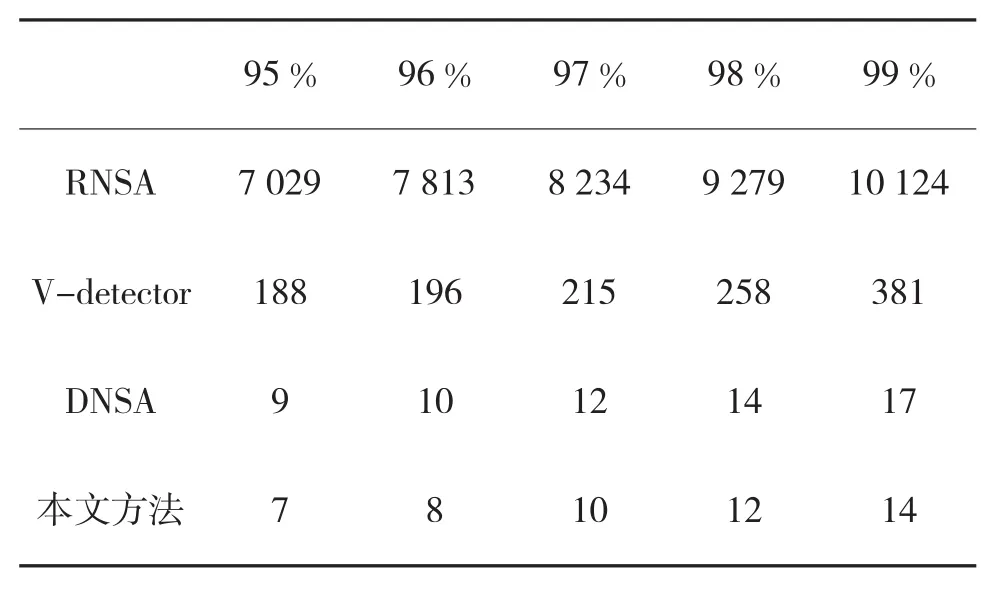
表1 4种方法的成熟检测器数量比较

显然，随着覆盖率水平的提高，4种方法对应的成熟检测器数量均出现了相应的增加；然而，同其他两种方法相比，DNSA与本文方法的增长幅度明显缓慢，体现出这两种方法良好的鲁棒性和优越的检测性能，尤其是在覆盖率达到99%时，经典RNSA对应的成熟检测器达到10 124，V-detector指标为381，而DNSA和本文方法的对应指标值仅为17和14。

3.3 检测率与误报率比较实验

在估计覆盖率一定的前提下，检测率的高低也是一项重要指标。表2、表3分别给出了估计覆盖率在90%～100%范围内时包括本文方法在内的4种方法对应的检测率结果和误报率结果。

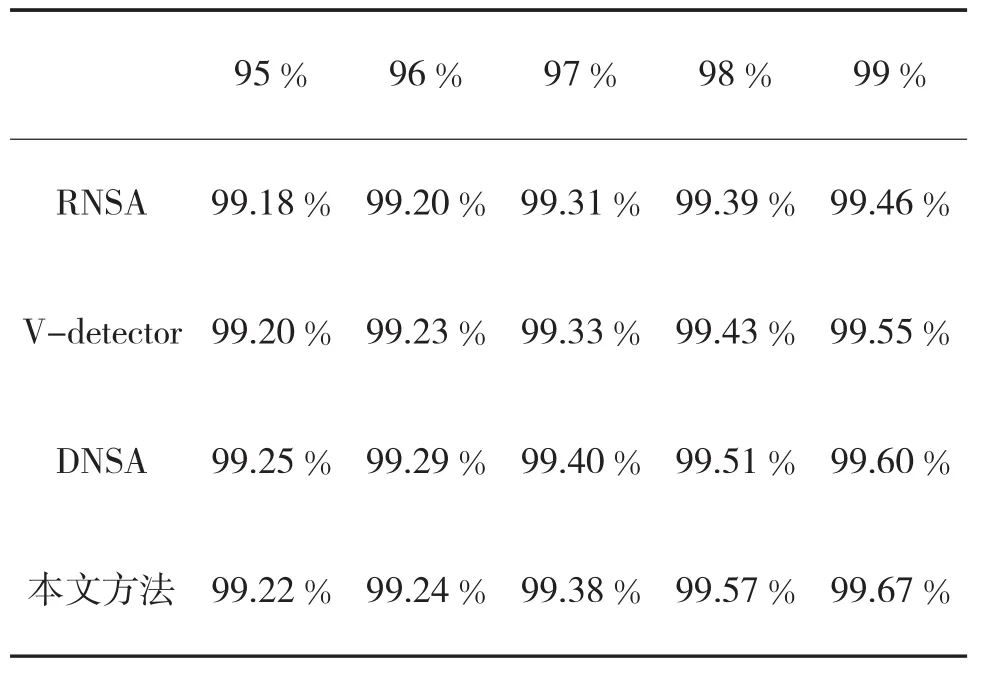
表2 4种方法的对应检测率比较结果

表3 4种方法的对应误报率比较结果

显然，随着估计覆盖率水平的提高，4种方法对应的检测率与误报率均相应增加。当估计覆盖率超过95%时，4种方法的检测率均超过了99%，获得了较为理想的检测结果，然而，4种方法对应的误报率表现却大相径庭，例如当估计覆盖率达到99%时，4种方法的误报率分别为55.92%，45.59%，22.12%和16.24%。显然，本文方法在保证较高检测器的同时具有最佳的误报率水平。

3.4 运行时间比较实验

表4给出了4种方法在估计覆盖率为95%前提下各自的平均运行时间，每组数据均进行3次仿真并取平均值。

表4 4种方法的平均运行时间比较

4种方法中，RNSA最为耗时，V-detector方法次之，DNSA方法运行时间最短，而本文方法为次优，主要原因在于本文方法不同于DNSA方法对未通过训练自体集耐受训练候选检测器的处理方案，引入了“剪切”机制对“有瑕疵”的候选检测器进行了切割，最终对成熟检测器集合还进行了优化处理，因此，在运行时间上要略长于DNSA方法。

4 结论

本文提出了一种基于二次否性剪切选择的入侵检测方法。该方法包含了成熟检测器耐受训练过程、训练自体集耐受训练过程以及成熟检测器集合优化过程3个重要环节，力求使用数量尽可能少、半径尽可能大的检测器覆盖尽可能大区域的非自体集合以提升整个入侵检测系统的综合性能。理论分析和仿真实验结果表明，同现有的几种经典方法相比，本文提出的方法具有更高的检测率、更低的误报率以及更少的检测器数量。