径向阵列艾里涡旋光在倾斜大气湍流中的漂移特性

李 怡,楚兴春,唐翰玲,赵尚弘

(空军工程大学信息与导航学院,陕西 西安 710077)

1 引 言

当激光束通过大气传播时,由于大气湍流的影响,波束的瞬时中心会在接收平面内随机移位,产生光束漂移现象[1]。与光强闪烁和光束扩展一样,光束漂移是激光束在大气湍流中传播的一个重要特性,它决定了激光束在自由空间光通信、激光测量和成像等实际应用中的效能[2-5],对各种不同模式光束的光束漂移研究近年来已有报道。Yu等[6]研究了电磁Gaussian-Schell模型光束(GSMB)在大气湍流中的光束漂移。王晓章等[7]用多相位叠加的方法模拟了艾里光束在Kolmogorov湍流中光斑质心漂移,并与高斯光束进行了比较。陈盼盼等[8]基于拓展的惠更斯-菲涅尔原理研究了圆对称阵列高斯光束在各项异性湍流大气传输时的漂移特性。

近年来,不少研究者基于艾里光束和光学涡旋的独特性质,将光学涡旋植入到艾里光场以得到艾里涡旋光束,并对其传输和漂移特性进行了研究[9-12]。Dai等[13-14]研究了叠加单位拓扑电荷光学涡旋的艾里光束在真空中的传播动力学。Wen等[15]研究了具有螺旋相位的艾里光束在湍流中的光束漂移,并讨论了拓扑电荷和湍流内尺度等对光束漂移特性的影响。程振等[16]采用多相位屏法模拟了艾里涡旋光束在大气湍流中的漂移特性,表明阵列艾里涡旋光束的漂移小于单束艾里涡旋光束的漂移。Aksenov等[17]研究了在均匀湍流大气中传播的艾里涡旋光束的随机漂移特性,表明光束在空间中占据的体积越大,光束漂移的方差就越小。赖松陶等[18]通过将离轴双光学涡旋引入到环形艾里光阵列提出并制备了环形阵列艾里涡旋光束(CAAVB),发现加载光学涡旋能明显提高CAAVB的光场强度。

目前,艾里涡旋光束通过大气湍流漂移特性的研究多是针对水平传播路径,而激光束沿倾斜路径穿过大气湍流传播的研究对于光学通信、激光雷达和军事应用等非常重要。本文采用von Karman湍流功率谱模型,应用等Rytov指数间隔多相位屏法,研究RAAVB沿倾斜路径通过大气湍流时的漂移特性,对比并分析了拓扑荷、天顶角、外尺度和涡旋离轴距离对光束漂移的影响。

2 理论分析

二维艾里光束可由X-Y平面上两个一维艾里光束相乘得到,其在源平面上的场为[19]:

(1)

式中,x0,y0为X和Y方向的横向尺度因子;φ为电场包络;Ai(·)为理想艾里函数;a为衰减因子且满足0≤a<1。

将n束二维艾里光均匀分布在X-Y平面的一个圆上,即可以得到径向阵列艾里光束(RAAB),第i(i=1,2…,n)束二维艾里光束在X-Y平面上的坐标为(xi,yi),可通过坐标变换公式得到,

(2)

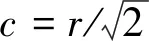
在z=0处,将光学涡旋加入RAAB即可得到RAAVB初始场:

[(x-xp)+i(y-yp)sign(x)]|p|

(-xsinαj+ycosαj+c),z=0]·

[(x-xp)+i(y-yp)sign(x)]|p|

(3)

式中,φ为光束电场包络;φj为第j束二维子艾里光束的电场;sign(·)为符号函数;p为光学涡旋拓扑荷;(xp,yp)为光学涡旋中心在X-Y平面上的坐标。

对激光束在大气湍流中传输的研究方法,主要有广义惠更斯-菲涅尔原理[20]、Rytov相位近似法[21]、分布傅里叶算法[22]和多层相位屏法[23]。在研究光束过倾斜大气湍流的研究方法中,通常采用相位屏法来模拟湍流。当传播路径较长时,发射器和接收器之间的湍流波动较大,单相屏近似会产生较大的误差。在这种情况下,整个路径可以分为多个区间,每个区间满足单个相位屏近似,前后相邻两个相位屏的场可表示为[23]:

F{exp[iψ(x,y,zj)]u(x,y,zj-1)}}

(4)

式中,F和F-1分别为傅里叶变换和反变换;zj-1、zj和Δzj分别为第(j-1)个和第j个相位屏的位置及它们之间的距离;κx和κy为X和Y方向上的空间波数;ψ(x,y,zj)为第(j-1)个相位屏产生的相位扰动。

由于光束沿倾斜路径传播,湍流强度随传播高度变化,因此本文采用等Rytov指数间隔相位屏法(ERPS)设置相位屏间隔Δz,其可根据湍流强弱设置密疏相间的相位屏,能很好地对不同折射率起伏区进行充分采样,光束传播示意图如图1所示,θ为天顶角。文献[24]证明了其对于光束沿倾斜路径通过大气湍流研究是可靠的,ERPS具体可表示为[24]:

(5)

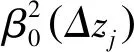
图1 等Rytov指数间隔多相位屏法模拟激光沿倾斜路径传播示意图Fig.1 Diagram of simulating laser propagation along slanted path by equivalent Rytov index-interval multi-phase screens method

本文采用van Karman功率谱进行功率谱反演模拟相位屏:

(6)

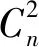
(7)

式中,h=zcos(θ)为高度;v为风速(通常取21m/s);C为底层大气折射率结构常数(通常取1.7×10-14m-3/2)。

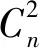
图2 不同天顶角下相位屏设置和与传播距离的关系曲线Fig.2 Phase screen number and versus propagation distance under different zenith angles

3 数值仿真及结果分析

3.1 参数设置

使用等Rytov指数间隔多相位屏法模拟RAAVB在大气湍流中沿倾斜路径传播,考虑到实际的应用场景,仿真参数的取值如表1所示。

表1 数值仿真参数Tab.1 Parameter values in numerical simulation

3.2 径向阵列艾里涡旋光束传输特性

当xp=yp=0,可产生轴上型RAAVB,其在z=0、1000、2000、4600 m平面处长曝光下的强度分布如图3所示。当p=0时,RAAVB即为环形艾里阵列光束,从图3(a1)可以看出,在初始面(z=0)处,其强度中心形成了半径为28.3mm的空心圆环。但当p≠0时,如图3(b1)所示,在初始面处,RAAVB强度分布中心出现空心暗核,且其强度明显小于环形艾里阵列光束。对比图3(a1)～(b4)发现,两种光束在传播过程中均保持低能量传播,随着传播距离增大,RAAB中心圆环半径和RAAVB暗核半径逐渐缩小；当传播至4600 m处时,RAAB和RAAVB均发生聚焦,且焦点处光强急剧增强,形成了高能光斑,但由于RAAVB中螺旋相位的存在,其在聚焦面处强度分布仍为环状结构。由于大气湍流的作用,RAAB和RAAVB在传播过程中的强度分布均产生明显畸变,且在聚焦位置前,畸变程度随传播距离的增大而增大。

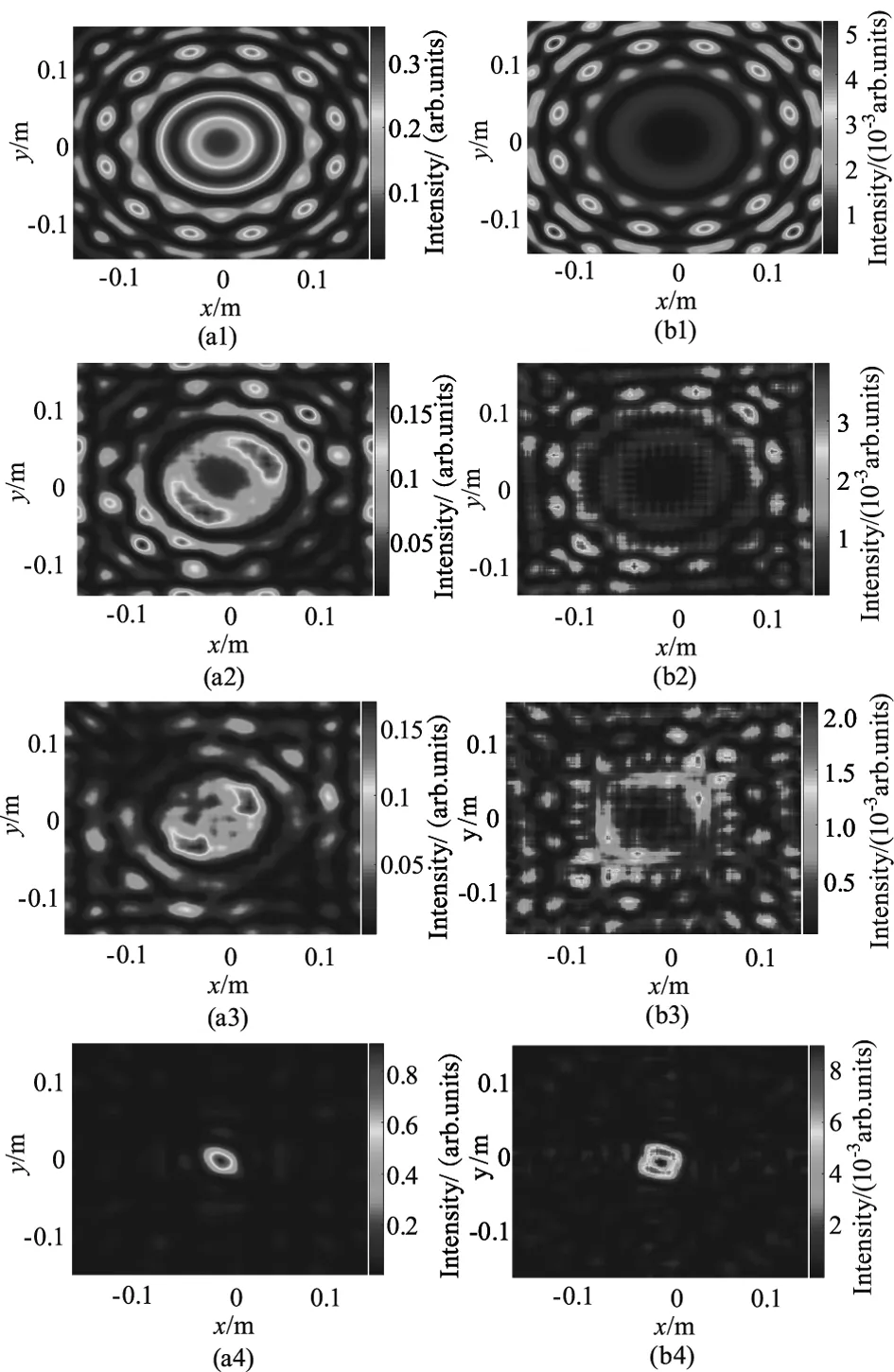
图3 z=0、1000、2000、4600m平面处轴上型RAAVB长曝光下的强度分布(θ=30,L0=50 m)(a1)～(a4)p=0;(b1)～(b4)p=1Fig.3 Intensity distributions of on-axis RAAVB at z= 0,1000,2000,600 m,θ=30,L0=50m

3.3 轴上型RAAVB的漂移特性

光束传播至距离z处时,其在X-Y平面上的质心坐标(xc,yc)定义为[7]:

(8)

光束质心的相对漂移量d定义为光束在湍流中传播的质心与在自由空间中传播的质心的相对距离

(9)

其中,(x0,y0)和(x1,y1)分别为光束通过自由空间和倾斜大气湍流后的质心坐标。

分析不同拓扑荷、天顶角、湍流外尺度对轴上型RAAVB光束过倾斜大气湍流的漂移特性影响,为了方便对比分析,计算了RAAB的质心漂移变化,同时对比了轴上型和离轴型RAAVB光束的漂移特性,由于相位屏模拟的随机性,下文中提到的质心漂移量均是30组数据的平均值。

(1)不同拓扑荷

选择拓扑荷p分别为0、1和2,不同天顶角下光束质心漂移量随传播距离的变化情况如图4所示。可以看出,光束传播至一定距离后,RAAVB的漂移量总是小于RAAB,且拓扑荷p越大,光束质心漂移量越小,即光束漂移受湍流的影响越弱；但p=2时的漂移量总是在开始传播后快速增大,然后保持稳定。原因在于:RAAVB涡旋半径随着p增大而增大,对中心能量削减增大,因此在初始传播阶段p越大,同样的湍流大小对光束的影响越大,但随着光束传播至聚焦平面,光束中心强度增大,湍流对光束的影响逐渐减弱,因此其质心漂移效应减弱。

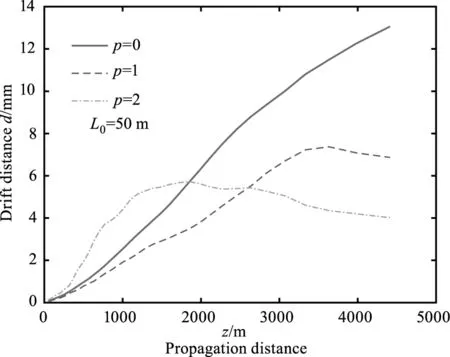
(a)θ=0°

(2)不同天顶角

选择天顶角θ分别为0°、30°和90°,不同拓扑荷下光束质心漂移量随传播距离的变化情况如图5所示。对比图5(a)～(c)可知,光束在湍流大气中沿倾斜路径传播的天顶角越大,质心漂移量越大,表明光束漂移现象受湍流的影响越严重；光束在θ=0°时的漂移量最小,在θ=90°时的漂移量最大,即光束沿垂直路径通过大气湍流时漂移受湍流影响最弱,沿水平路径传播时受湍流影响最大。这是因为天顶角越大,光束传播同样距离的高度越高,由公式(7)可知,此时大气结构常数越小,因此光束漂移受湍流影响越小。

由图5可知,当p=0、1、2,天顶角从90°变化为0°,光束传播至4600 m时漂移量分别减小约6 mm、7 mm、5 mm；当θ=0°、30°、90°时,拓扑荷从0增大到2,光束传播至4600 m时漂移量减小约9 mm、11 mm、10 mm,这说明相较于天顶角,拓扑荷对光束漂移现象影响更大,增大拓扑荷,光束漂移量明显降低。

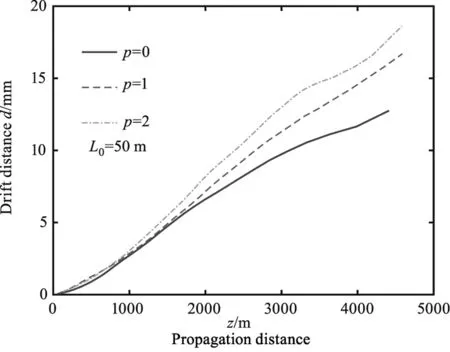
(a)p=0

(3)不同大气湍流外尺度

当θ=30°时,选择湍流外尺度L0分别为10、30、80 m,不同拓扑荷下光束质心漂移量随传播距离的变化情况如图6所示。由图6可知,湍流外尺度越大,光束漂移量越大,这是因为随着湍流外尺度增大,湍流中包含的能量也增大,其对光束漂移的影响增大。

(a)p=0

3.4 离轴型RAAVB漂移特性

设置涡旋中心坐标(xp,yp)≠(0,0)时,可产生离轴型RAAVB,涡旋中心坐标为(0.02,0.02)的离轴RAAVB在不同传播距离处长曝光下的强度分布如图7所示,从图7可以看出由于涡旋中心改变,强度分布的暗核中心也移至右上角,且光束在初始面的强度分布不再为圆形对称分布。

图7 z=0、1000、2000、4600 m平面处离轴型RAAVB长曝光下的强度分布,θ=30°,L0=50 m,p=1Fig.7 Intensity distributions of off-axis RAAVB at z= 0,1000,2000,600 m,θ=30°,L0=50 m,p=1

选择涡旋中心位置xl=yl=0、0.02、0.04、0.08 m,不同天顶角下光束质心漂移量随传播距离的变化情况如图8所示。由图8可以看出,当xl=yl=0时,光束漂移量最小,且光束漂移量随着离轴距离的增大而增大,这意味着,离轴RAAVB的漂移现象比轴上型RAAVB受湍流影响更严重,且涡旋中心偏离光束中心越远,RAAVB的漂移特性受湍流影响越大。

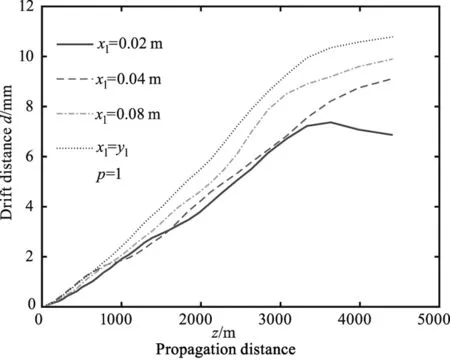
(a)θ=0°

4 结 论

本文采用等Rytov指数间隔多相位屏法数值模拟了RAAVB沿倾斜路径通过大气湍流时的漂移特性,并与阵列艾里光的漂移现象做了比较。结果表明,相比于阵列艾里光束,RAAVB的漂移现象受湍流影响更小；光束漂移量随拓扑荷的增大而减小,随天顶角和湍流外尺度的增大而增大；且相较于天顶角和湍流外尺度,拓扑荷对光束漂移现象影响更大；离轴RAAVB的漂移现象比轴上型RAAVB受湍流影响更严重,且漂移距离随涡旋离轴距离的增大而增大。该研究结果对于艾里涡旋光束在光通信、激光雷达等领域的应用具有一定的参考意义。