克尔介质中艾里孤子的形成及控制

秦旭磊， 李雪健， 陈卫军， 李 野， 杨继凯

(长春理工大学 理学院， 吉林 长春 130022)



克尔介质中艾里孤子的形成及控制

秦旭磊， 李雪健， 陈卫军*， 李 野， 杨继凯

(长春理工大学 理学院， 吉林 长春 130022)

利用分步傅里叶法，数值研究了艾里光束在自聚焦克尔非线性介质中的传输。结果表明，当较强的非线性作用于艾里光束时，主瓣能量在传输过程中会发生脱落形成具有周期振荡的空间孤子。随着非线性的增强，该孤子的振荡周期与半高宽都减小。调节艾里光束的入射角度时，脱落孤子的传输轨迹随之发生变化，不同于艾里光束的是，艾里孤子的传输始终保持直线传输。

非线性光学； 克尔介质； 艾里孤子

1 引 言

近年来，艾里光束一直是国内外物理学者们的研究热点。1979年，Berry和Balazs[1]在量子力学范畴内提出了无展宽且横向自加速的艾里函数是薛定谔方程的一个特解，理论上艾里函数是无穷振荡函数，因此具有这种解的粒子应该具有无穷的能量。显然，这在实际中并不存在。2007年，Siviloglou等[2]理论上给出了一种用指数衰减函数描述的有限能量艾里光束可以作为波动方程的解，并在随后的实验中首次观察到了有限能量艾里光束[3]。从此，艾里光束以其独特的性质(准无衍射、横向自加速及自愈等)在光学微粒操控[4-5]、光路由[6]、弯曲等离子体通道产生[7]、大气通信[8]、光子弹[9-10]以及光束自聚焦合成[11]等方面展现了非常广阔的应用前景。

艾里光束在传输过程中区别于其他无衍射光束的最大特点就是横向自加速特性。因此，近些年出现了许多关于艾里光束的传输控制的文献报道[12-22]。一方面，在线性折射率调制的作用下，艾里光束的传输可以按照预定的轨迹进行；另一方面，在非线性折射率的调制下，艾里光束的传输受到非常大的影响，例如，Jia等[17]在无偏压光折变介质中通过实验观察到了自陷的局域艾里光束，结果表明介质的扩散非线性可以抵消艾里光束在传输过程中的自加速作用。Fattal等[20]从理论上证明了艾里脉冲在克尔介质中传输时可以脱落形成孤子。Zhang等[21]研究了艾里光束在克尔和饱和非线性介质中的交互作用，发现在传输过程中会产生呼吸孤子或孤子对。

本文研究了自聚焦克尔非线性的折射率调制对于艾里光束传输的影响，重点分析空间艾里孤子的形成及影响条件，并讨论艾里孤子的传输控制方法，为艾里光束在实际中应用提供理论基础。

2 理论分析

假设一高斯光束经过立方相位掩膜产生的艾里光束[3]沿z轴传播，在傍轴近似下，艾里光束电场的慢变复振幅包络φ满足的演化方程为[21]：

(1)

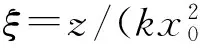
(2)

上式中，a>0是衰减系数(保证艾里光束具有有限能量)，Ai(·)表示的是艾里函数。图1(a)给出了艾里光束的光场模式分布，蓝色虚线表示的是a=0，即理想的艾里光束(具有无穷振荡能量)；红色实线表示的是a=0.1，即截断艾里光束(具有有限能量)。图1(b)是(a)中光场模式对应的强度分布图。图1(c)和(d)分别为理想艾里光束和有限能量艾里光束在自由空间中的传输演化情况。

图1 理想艾里光束(a=0)与有限能量艾里光束(a=0.1)的光场分布(a)和强度分布(b)，以及自由空间中艾里光束(c)与有限能量艾里光束(d)的传输。

Fig.1 Light field profile (a) and intensity profile (b) of the ideal Airy beam (a=0) and finite energy Airy beam (a=0.1), and the propagation of the ideal Airy beam (c) and the finite energy Airy beam (d) in free space, respectively.

3 结果与讨论

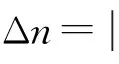
图2 自聚焦克尔非线性介质中艾里光束的传输，(a)A0=1.5，(b)A0=2.4，(c)A0=3，其他参数：a= 0.1;(d)A0取不同值时脱落艾里孤子的半高宽随传输距离变化的函数关系。

Fig.2 Propagation of Airy beams in self-focusing Kerr nonlinear media, (a)A0=1.5, (b)A0=2.4, (c)A0=3, other parameter:a= 0.1. (d) FWHM of the shedding Airy soliton as function of propagation distant with different values ofA0.

从图2(a)可以看出，当A0较小时，克尔非线性响应比较弱，对艾里光束传输的影响并不明显，传输轨迹基本保持抛物线形。逐渐增加A0发现，艾里光束在传输大约2 m后，从主瓣位置(第一波瓣)沿z轴出现能量脱落，形成类正曲双割(Hyperbolic-secant)形孤子，该孤子呈现出周期振荡的特性，且传输距离较远，如图2(b)所示，本文中称该孤子为空间艾里孤子。当A0足够大时，如图2(c)所示，克尔效应非常强，空间艾里孤子宽度非常小，振荡周期也变得非常小。图2(d)给出了A0取不同值时孤子的半高宽随传输距离的变化情况。值得注意的是，当空间艾里孤子形成时，在x正半轴空间还存在部分艾里光束的末尾，该末尾保持艾里光束在自由空间中的传输轨迹。

从上述结果可知，空间艾里孤子的形成与入射光的初始振幅有关，只有在一定强度的非线性折射率调制下才能在克尔介质中形成空间艾里孤子。然而，上述空间艾里孤子都是沿着z轴向前传输。接下来研究空间艾里孤子的传输轨迹控制方法。由文献[18]可知，在初始场分布函数加上与入射角度相关的因子，则光场分布表达式变为：

φ(η,ξ=0)=A0Ai(η)exp(aη)exp(ivη),

(3)

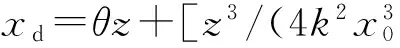
从图3(a～c)可以看出，当v取不同值时，自由空间中传输的艾里光束的横向偏移发生了变化，该方法可用来控制艾里光弹的传输轨迹[18]。当这样的艾里光束入射到克尔非线性介质中时，空间艾里孤子的传输同样也产生了偏转，结果如图3(d～f)所示。当v=-1(θ≈-0.8 mrad)时，脱落孤子向-x方向偏转；当v=0(θ≈0 mrad)时，无偏转；当v=1(θ≈0.8 mrad)时，脱落孤子向x方向偏转。由此可见，可以通过调节θ值的大小来控制空间艾里孤子的传输方向。值得注意的是，空间艾里孤子不同于艾里光束，其传输轨迹在较强自聚焦克尔非线性下始终保持直线。

图3 (a～c)自由空间中不同入射角度艾里光束的传输，v=-1, 0, 1,A0=1,a=0.1;(d～f)克尔非线性介质中空间艾里孤子的偏转，v=-1, 0, 1,A0=2.5,a= 0.1;(g～i)是对应于(d～f)中白色虚线位置处脱落孤子的强度图。

Fig.3 (a-c) Propagation of Airy beams with different launch angles in free space,v=-1, 0, 1,A0=1,a=0.1. (d-f) Deflection of Airy solitons in Kerr nonlinear media,v=-1, 0, 1,A0=2.5,a= 0.1. (g-i) Intensities of the shedding solitons at the position of white dashed lines corresponding to (d-f).

4 结 论

本文数值研究了有限能量艾里光束在自聚焦克尔非线性介质中的传输。结果发现，在较强非线性的影响下，艾里光束的主瓣能量在传输过程中脱落形成具有周期振荡的空间孤子。随着非线性的增强，孤子的振荡周期和宽度逐渐变小。在孤子的形成过程中，艾里光束在其横向加速方向始终具有艾里末尾，艾里末尾的轨迹与自由空间中的艾里光束一致。当艾里光束的入射角度发生变化时，模拟发现克尔非线性介质中脱落艾里孤子的传输方向也随之发生变化。由此可见，调节入射光的角度可以控制脱落孤子的传输方向。与艾里光束不同的是，孤子的传输轨迹始终保持直线传输。

[1] BERRY M V, BALAZS N L. Nonspreading wave packets [J].Am.J.Phys., 1979, 47(3):264-267.

[2] SIVILOGLOU G A, CHRISTODOULIDES D N. Accelerating finite energy Airy beams [J].Opt.Lett., 2007, 32(8):979-981.

[3] SIVILOGLOU G A, BROKY J, DOGARIU A,etal.. Observation of accelerating Airy beams [J].Phys.Rev.Lett., 2007, 99(21):213901-1-4.

[4] 程化,臧维平,田建国. 艾里光束对微小颗粒的捕获和输运研究 [J]. 光学学报, 2011, 31(S1):100405.

CHENG H, ZANG W P, TIAN J G. Study on optical trapping and propulsion of small particles by Airy beam [J].ActaOpt.Sinica, 2011, 31(S1):100405. (in Chinese)

[5] BAUMGARTL J, MAZILU M, DHOLAKIA K. Optically mediated particle clearing using Airy wavepackets [J].Nat.Photon., 2008, 2(11):675-678.

[6] ROSE P, DIEBEL F, BOGUSLAWSKI M,etal.. Airy beam induced optical routing [J].Appl.Phys.Lett., 2013, 102(10):101101-1-3.

[7] POLYNKIN P, KOLESIK M, MOLONEY J V,etal.. Curved plasma channel generation using ultraintense Airy beams [J].Science, 2009, 324(5924):229-232.

[8] CHEN C Y, YANG H M, KAVEHARD M,etal.. Propagation of radial Airy array beams through atmospheric turbulence [J].Opt.LasersEng., 2014, 52:106-114.

[9] ABDOLLAHPOUR D, SUNTSOV S, PAPAZOGLOU D G,etal.. Spatiotemporal Airy light bullets in the linear and nonlinear regimes [J].Phys.Rev.Lett., 2010, 105(25):253901.

[10] 任志君,吴琼,周卫东,等. 空间诱导产生艾里-贝塞尔光弹研究 [J]. 物理学报, 2012, 61(17):174207-1-7.

REN Z J, WU Q, ZHOU W D,etal.. Spatially induced Airy-Bessel light bullets [J].ActaPhys.Sinica, 2012, 61(17):174207-1-7. (in Chinese)

[11] 张泽,刘京郊,张鹏,等. 多艾里光束合成自聚焦光束的实验实现 [J]. 物理学报, 2013, 62(3):034209-1-6. ZHANG Z, LIU J J, ZHANG P,etal.. Generation of autofocusing beams with multi-Airy beams [J].ActaPhys.Sinica, 2013, 62(3):034209-1-6. (in Chinese)

[12] EFREMIDIS N K. Airy trajectory engineering in dynamic linear index potentials [J].Opt.Lett., 2011, 36(15):3006-3008.

[13] BESIERIS I M, SHAARAWI A M. Accelerating Airy beams with non-parabolic trajectories [J].Opt.Commun., 2014, 331:235-238.

[14] KOTLYAR V V, KOVALEV A A. Airy beam with a hyperbolic trajectory [J].Opt.Commun., 2014, 313:290-293.

[15] XIAO F J, LI B R, WANG M R,etal.. Optical Bloch oscillations of an Airy beam in a photonic lattice with a linear transverse index gradient [J].Opt.Express, 2014, 22(19):22763-22770.

[16] ZHANG P, WANG S, LIU Y M,etal.. Plasmonic Airy beams with dynamically controlled trajectories [J].Opt.Lett., 2011, 36(16):3191-3193.

[17] JIA S, LEE J, FLEISCHER J W,etal.. Diffusion-trapped Airy beams in photorefractive media [J].Phys.Rev.Lett., 2010, 104(25):253904-1-4.

[18] SIVILOGLOU G A, BROKY J, DOGARIU A,etal.. Ballistic dynamics of Airy beams [J].Opt.Lett., 2008, 33(3):207-209.

[19] 程振,楚兴春,赵尚弘,等. 艾里光束传输轨迹控制方法的研究进展 [J]. 激光与光电子学进展, 2015, 52(6):060002-1-8.

CHENG Z, CHU X C, ZHAO S H,etal.. Research progress of Airy beam’s propagation trajectory control [J].LaserOptoelectron.Progress, 2015, 52(6):060002-1-8. (in Chinese)

[20] FATTAL Y, RUDNICK A, MAROM D M. Soliton shedding from Airy pulses in Kerr media [J].Opt.Express, 2011, 19(18):17298-17307.

[22] 王晓章. 基于相位空间光调制器的艾里光束产生和传输控制研究 [D]. 哈尔滨:哈尔滨工业大学, 2013.

WANG X Z.ResearchonGenerationofAiryBeamsandPropagationControlledbyUsingSpatiallightModulator[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese)

秦旭磊(1981-)，男，吉林长春人，博士，讲师，2015年于长春理工大学获得博士学位，主要从事微电子及光电子技术的研究

E-mail: qxl@cust.edu.cn陈卫军(1988-)，男，陕西咸阳人，硕士，2013年于天津工业大学获得硕士学位，主要从事非线性光学及光电成像方面的研究。

E-mail: dk062chenweijun@163.com

Formation and Control of Airy Soliton in Kerr Media

QIN Xu-lei, LI Xue-jian, CHEN Wei-jun*, LI Ye, YANG Ji-kai

(SchoolofSciences,ChangchunUniversityofScienceandTechnology,Changchun130022,China)

*CorrespondingAuthor,E-mail:dk062chenweijun@163.com

The propagation of Airy beams in self-focusing Kerr nonlinear media was investigated numerically by using split-step Fourier method. It is shown that spatial soliton with periodic oscillation can be formed out of the centered energy about the Airy main lobe during the propagation on the influence of stronger nonlinearity. With the increasing of the nonlinearity, the periodic and full width at half maximum (FWHM) of the soliton are decreased. The propagation trajectory of the shedding soliton is changed when the initial launch angle of Airy beam is adjusted. Different from Airy beams, the propagation of the Airy soliton is always maintaining straight line.

nonlinear optics; Kerr media; Airy soliton

1000-7032(2016)10-1281-06

2016-04-10；

2016-05-11

国家自然科学基金(51502023)资助项目

O437

A

10.3788/fgxb20163710.1281