激光熔覆再制造车轮损伤及寿命评估研究

华 亮,田 威

(1.南京铁道职业技术学院机车车辆学院,江苏 南京 210031;2.南京航空航天大学机电学院,江苏 南京 210016)

1 引 言

伴随着我国轨道交通行业的快速发展,轨道交通移动装备的需求日益增多。高速重载情况下,铁道机车车辆车轮和钢轨间的磨耗更为严重,由之造成大量车轮产生疲劳裂纹、踏面擦伤等损伤,大大增加了轨道装备企业检修工作量。车轮磨耗到限后,一般是将其高温回炉重新冶炼,既浪费了能源,又造成了不必要的环境污染,故而若能利用“加材料”的方式修复磨耗到限的车轮,恢复其原有形貌及性能,并重新使用,则可减少污染、节约能源、大量节省时间和人工成本。

激光熔覆技术已经在机械[1]、航空航天[2]领域取得了较为广泛的应用,亦有不少科研工作者在轨道交通领域做出了有益尝试。Wang W J等人[3]将激光熔覆技术应用于轮轨材料的修复,重点研究激光熔覆后试件的硬度及耐磨性,研究结果表明激光熔覆后的车轮和钢轨试件的显微硬度显著提高40 %以上,且耐磨性能达到轮轨基体材料的4倍。丁阳喜等人[4]对激光熔覆修复高速列车轮对磨耗问题进行了研究,确定了正交试验最优工艺参数,研究表明熔覆试件硬度及耐磨性均有较大幅度提升。慕鑫鹏等人[5]在轮轨材料上分别熔覆钴基和铁基合金,研究了熔覆涂层微观组织结构、硬度及残余应力分布,滚动接触疲劳试验发现两类涂层试件的磨损性能均有较大提升,相对而言钴基涂层的性能更好。

侯有忠等人[6]对激光熔覆再制造动车组车轴的可行性进行了研究,选定了熔覆材料、确定了再制造工艺,再制造试件压装试验表明再制造车轴满足动车组轮对压装要求。P.Lu等人[7]对激光熔覆钢轨的磨耗特性进行了研究,发现在R200钢上熔覆马氏体不锈钢粉末后,其磨损特性较单纯使用R260钢有较大提升。

科研工作者在轨道交通领域的研究成果对激光熔覆再制造机车车辆关键零部件的研究很有借鉴意义,不过现有研究成果多处于试验室阶段,还没有科研工作者将激光熔覆技术直接应用于机车车辆轮对的修复。本文直接对损伤车轮进行了激光熔覆再制造,建立了激光熔覆车轮磨耗损伤及寿命评估模型,并对激光熔覆车轮损伤及寿命进行了定量评估。

2 激光熔覆再制造车轮

机车车辆轮对常见损伤主要有车轮踏面擦伤与剥离、轮缘或轮辋疲劳裂纹及裂损等。修复损伤车轮的主要方法是璇修,即实际应用中一般采用“减材料”的方式加工损伤车轮,无形中会造成材料的极大浪费。如果能够采用激光熔覆技术对损伤部位进行修复,即采用“加材料”的方式修复损伤轮对,则可大幅减少材料的浪费,亦对节约能源、降低环境污染有明显成效。

本文采用激光熔覆技术对踏面擦伤车轮(图1)进行再制造。熔覆前采用丙酮清洗车轮踏面擦伤部位,并对熔覆粉末进行烘干处理。熔覆再制造车轮采用功率2000 W光纤激光器,电流I=210 A,脉宽τ=3.5 ms,频率f=15 Hz,熔覆扫描速度v=180 mm/min,送粉速率为6 g/s,激光光斑直径为2 mm,离焦量为+1.5 mm。再制造后的车轮如图2所示。

图1 车轮踏面擦伤Fig.1 Wheel tread abrasion

图2 熔覆再制造车轮Fig.2 Wheel remanufactured using laser cladding

3 再制造车轮损伤评估

现有评估车轮接触及磨耗损伤的模型主要有安定图评估模型和损伤函数评估模型两大类,但安定图评估模型没有考虑轮轨接触蠕滑率及磨耗与接触疲劳之间的相互影响,精度相对较低,故而本文采用基于磨耗数的损伤函数评估模型来评估车轮的损伤。

损伤函数评估模型既能考虑磨耗与接触疲劳损伤间的相互关系,又可以考虑蠕滑力和蠕滑率对车轮滚动接触疲劳损伤的影响,磨耗及疲劳损伤之和即为车轮转动一周引起的损伤。磨耗数Tγ按下式进行计算[8]:

Tγ=Txγx+Tyγy

(1)

式中,T和γ分别表示蠕滑力及蠕滑率,可由车辆动力学软件SIMPACK计算得出,纵向和横向分别用x、y表示。

车轮滚动接触疲劳损伤函数曲线如图3所示,损伤函数相关参数见表1。

图3 车轮滚动接触疲劳损伤函数[8]Fig.3 Damage function for rolling contact fatigue of the wheel[8]

现有研究成果表明损伤函数中的裂纹起始值与材料剪切屈服强度成正比[3],再制造车轮熔覆材料的剪切屈服强度约为473 MPa,车轮钢材料剪切屈服强度为300 MPa,熔覆再制造车轮裂纹起始值按比例关系可取为32 N。

疲劳裂纹扩展速度直接影响构件的疲劳寿命,故可依据基体与熔覆件疲劳之比来修正损伤函数中的裂纹速度参数。依据基体寿命和熔覆件寿命之比[9],再制造车轮裂纹速度可取为5.6×10-4r/N。

西南交大陶功权研究表明损伤函数中的耐磨系数和机械零部件硬度之间存在近似的线性关系[8],车轮钢平均硬度约为280 HV,本文再制造车轮熔覆层的显微硬度约为800HV,按硬度与磨耗数间的线性关系式可得激光熔覆车轮的磨耗起始值为285 N,磨耗速度为-1.9×10-6r/N。

由此,再制造车轮损伤函数各参数已确定,基体车轮及再制造车轮损伤函数参数见表1。

表1 车轮滚动接触疲劳损伤函数参数Tab.1 Parameters of the wheel′s rolling contact fatigue damage function

依据修正后的再制造车轮损伤函数参数值,即可计算出再制造车轮的磨耗数,进而可以确定熔覆车轮每滚动一周的复合损伤,据之即可计算出熔覆车轮全寿命周期的总损伤,其中熔覆再制造车轮的蠕滑率和和横纵向蠕滑力利用动力学仿真软件SIMPACK计算得出。

SIMPACK 软件轮轨模块经过大量铁路车辆试验验证,具有很高的仿真精度和效率,是全球铁路车辆系统动力学仿真的标准开发工具。仿真计算时以CRH2动车组为研究对象建立动力学模型,熔覆车轮踏面为LMA踏面,CN60钢轨,轮对内侧距1353 mm,建模时选用动车组前进方向、平行于轨道平面向右、垂直于轨道平面向下分别作为x轴、y轴和z轴,动力学模型如图4所示。动车组车体、构架(2个)、牵引拉杆(2个)、轮对(4个)均取纵向、横向、垂向、侧滚、点头、摇头等6个自由度；转臂(8个)取点头1个自由度,整个动车组系统动力学模型共有62个自由度。

动车组系统动力学方程的一般形式为[10]:

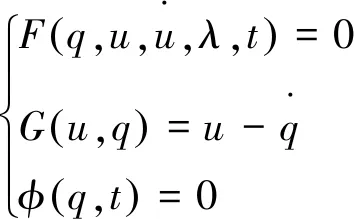
(2)

式中,u表示广义速度列阵；q表示广义坐标列阵；G表示广义速度的代数方程列阵；φ表示约束的代数方程列阵；λ表示约束力及作用力列阵；F表示系统力学微分方程。

图4 仿真计算用动力学模型Fig.4 Dynamic model for simulation

由于引起车轮磨耗及疲劳的主要原因是车辆频繁通过曲线,故而本文重点研究对象为曲线通过时车辆的动力学性能,以京津线实测数据作为轨道激励,动车组时速按200 km/h计算,轮径以新轮直径860 mm计算,曲线选用右曲线,仿真计算时间20秒,具体见表2。

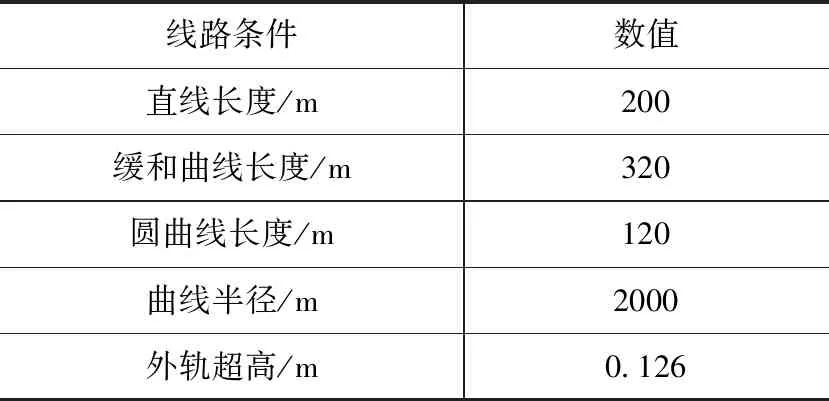
表2 仿真计算选用的线路条件[9]Tab.2 Line conditions for the simulation[9]

仿真计算得到的纵横向蠕滑力及蠕滑率曲线如图5～8所示(轮对1内侧车轮)。

从图5～8展示的计算结果可以看出轮对内侧车轮的纵向和横向蠕滑力较大,其合力即轮轨切向力也较大,容易造成轮对踏面产生裂纹,且轮对内侧车轮纵向蠕滑力的方向与动车组运行方向相反,使得裂纹进入接触斑前处于张开状态,轮轨表面的液体如雨水等就可浸入裂纹中,由于液体的不可压缩性,会使得裂纹更容易扩展。

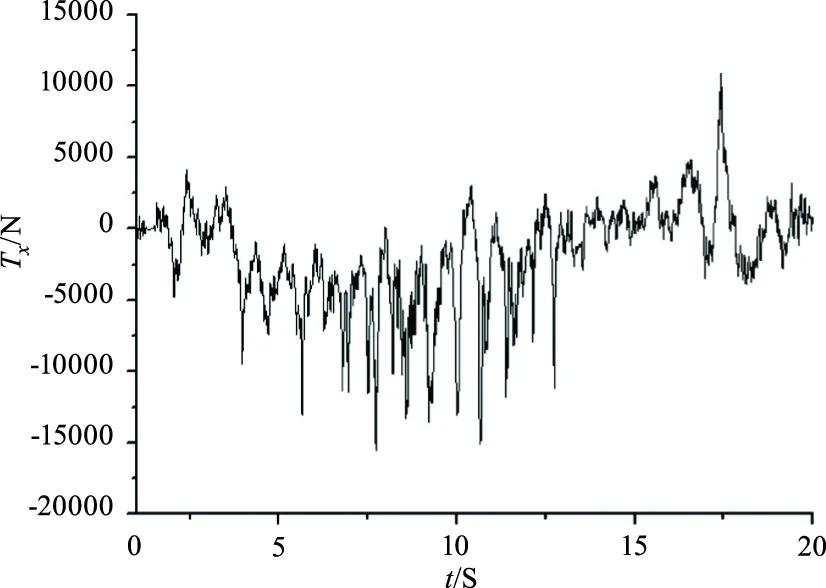
图5 车轮纵向蠕滑力Fig.5 Longitudinal creep force of the wheel

图6 车轮横向蠕滑力Fig.6 Lateral creep force of the wheel

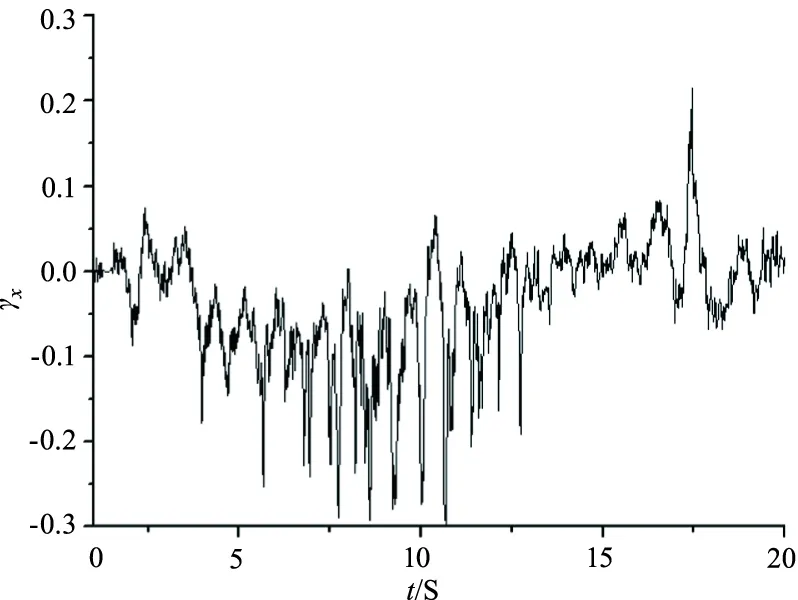
图7 车轮纵向蠕滑率Fig.7 Longitudinal creep rate of the wheel

由于线路曲线有左曲线和右曲线之分,线路亦有上行线和下行线之分,故而每个车轮都有机会处于内侧,因此,当运行里程达到一定限度后在动车组各个车轮上均易出现疲劳裂纹以及剥离现象,进而是轮对失效。

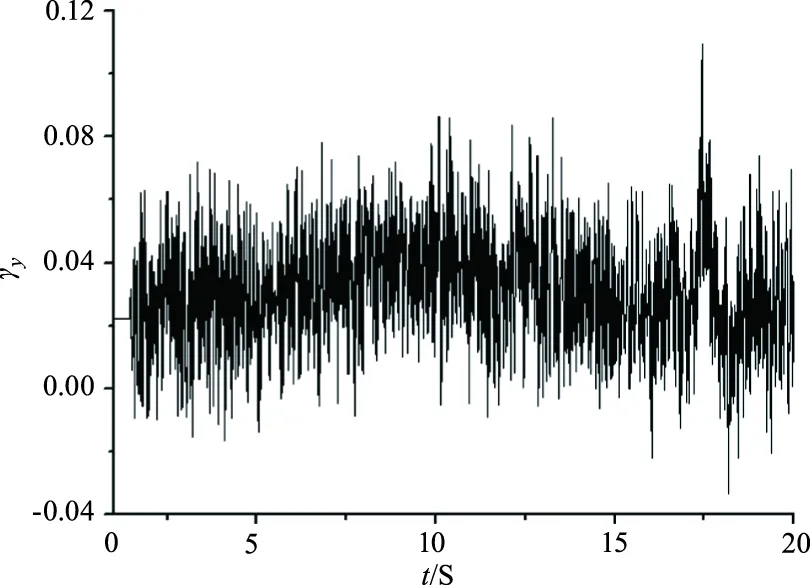
图8 车轮横向蠕滑率Fig.8 Lateral creep rate of the wheel

依据公式(1)计算可得熔覆车轮磨耗数的平均值为364 N。故经过本文给出的这段线路后激光熔覆再制造车轮产生的损伤Dw为:

Dw=[(364-32)×5.6×10-4-(364-285)×

1.9×10-6]×120/3.14/0.86=8.27×10-3

(3)

4 再制造铁路车轮寿命评估

Chaboche针对单轴疲劳问题提出了损伤与疲劳寿命之间的关系式[11]:

dD=[1-(1-D)β+1]α

(4)

式中,D表示损伤变量;N表示疲劳寿命;σa表示应力幅;σm表示平均应力;β,M0,b是由材料性质决定的参数;α是由损伤及载荷共同决定的参数,其表达式为[12-13]:

(5)

式中,如果x>0,则〈x〉=x；如果x≤0,则有〈x〉=0。表示最大应力;σR表示对应应力比R下的材料疲劳极限;σb表示材料强度极限;H和a均是实验常数,Dattoma等[12-13]建议金属材料H=0.0801,a=0.434。

已有研究表明,残余拉应力及裂纹闭合效应[14]均会对机械产品的疲劳寿命产生不容忽视的影响,故在评估激光熔覆损伤时考虑残余拉应力及裂纹闭合效应的影响,可以提高损伤模型精度。计入残余拉应力及裂纹闭合效应后,式(4)修正为:

dDcξ=[1-(1-ξDc)β+1]αc

(6)

式中,dDcξ表示计入裂纹闭合效应后的损伤;ξ为裂纹闭合有效因子。式中平均应力可修正为[15]:

σm=σm0+σrmax

(7)

式中,σm0为不计入残余拉应力时的平均应力。

不同应力比R所对应的裂纹闭合有效因子ξ可按下式计算[16]:

ξ=0.75+0.3R+0.15R2(-1≤R≤1)

(8)

设熔覆车轮的初始损伤为Dct,则有0

(9)

式中,材料常数取值为[9]:β=5.003,M0=3985.423,b=0.001。

车轮寿命评估时假定应力比R为-1,列车直线运行时车轮无损伤、轮轨接触斑面积为100mm2、运行线路中小曲线半径线路长度占线路总长的1 %。将式(2)计算得到的接触疲劳损伤作为熔覆再制造车轮初始损伤,代入公式(9)可得本文试验条件下再制造车轮可运行里程约164万千米,比车轮规定的200万km服役寿命略小,原因主要有两点:一是本文仿真计算采用的曲线半径较为苛刻,实际线路的曲线半径远大于文中选用的曲线半径,故而再制造车轮在实际线路上运行时损伤较小,运行里程更接近于车轮设计寿命；二是计算模型中的部分参数受激光熔覆工艺条件的影响较大,不同工艺参数再制造的车轮寿命也会有差异。

5 结 论

本文采用激光熔覆再制造技术修复了踏面擦伤车轮,结合车辆动力学分析,对现有铁路车轮损伤评估模型进行了修正,并以CRH2型动车组车轮为研究对象,建立了熔覆再制造车轮服役过程损伤及寿命评估模型。评估模型计算结果满足车轮设计要求,为铁路车轮的运用维修提供了一种新的思路,对铁路相关产业的发展有一定促进作用,亦为完善再制造工程理论体系提供了有益补充,具备较明显的科学意义和工程应用价值。