空气流量对煤粉-空气两相旋转爆轰波的影响

祝文超，王健平，王宇辉，李世全，杨 帆，相 博，张国庆

(1.北京化工大学 机电工程学院，北京 100029；2.北京大学 工学院，北京 100871；3.北京理工大学 宇航学院，北京 100081)

旋转爆轰发动机(Rotating Detonation Engine，RDE)通过爆轰燃烧产生热量工作，爆轰过程可以近似为等容循环，熵增较小，因此被广泛研究。理论上热效率比传统的爆燃发动机高出20%～25%[1]。采用氢气-空气的RDE燃料比冲可达5 000 s以上[2]，含收敛喷管的乙烯-氧气的RDE可获得73%～90%的最佳比冲[3]。与脉冲爆轰发动机(Pulse Detonation Engine，PDE)相比，RDE只需一次点火，便可实现爆轰波的连续传播，且对来流速度具有一定的适应性，有望成为未来高超声速推进的一个新选择。截至2014年，Aerojet Rocketdyne公司进行524次RDE的高温测试[4]，包括多种推进剂(气态和液态燃料)、多种喷嘴、多种喷管以及有无等离子体增强。目前RDE的研究主要通过压力测量技术[5-7]、流场可视化技术[8-11]以及计算工作[12-14]以帮助量化旋转爆轰波(Rotating Detonation Wave，RDW)的传播特性。

使用煤粉作为推进系统燃料的想法曾被几次提出，但未付诸实施，这一提出的主要思想是煤炭的价格低廉以及储存丰富等特点[15-16]，因此基于固态燃料的气固两相RDE近些年来成为旋转爆轰研究的一个热点课题[17-20]。实验研究方面，BYKOVSKII等[21-23]以煤和氢气为燃料，首先实现环形燃烧室内爆轰波的稳定传播，并获得气固两相RDW结构，证明了气固两相爆轰的可行性。BURKE等[24]将RDE与粒子播种机连接，分析了有机颗粒燃烧对爆轰波传播特性的影响，但结果并不显著。在随后的实验[25-26]中将碳黑(由1%的挥发分和99%的碳组成)添加到氢气-空气的RDE中，发现碳颗粒燃烧释放热量能够维持爆轰波传播，且燃烧热与碳颗粒添加量呈线性关系。关于气固两相RDW数值模拟研究[27]则相对较少，SALVADORI等[28]建立了固体颗粒和空气的两相爆轰模型，采用欧拉-欧拉稠密粒子公式模拟爆轰燃烧中离散相，结果表明煤颗粒的加入对流场没有较大的影响，爆轰波主要是依靠氢气和空气燃烧释放的热量来维持传播。

反应物的当量比是RDE参数研究的重要的因素之一。当量比变化时，反应物的能量释放率、爆轰波的传播速度、传播模态以及稳定性等均有所不同。在氢气-氧气的RDE实验和数值模拟[29]中，随着当量比的增大，爆轰波的速度先增大后减小，最大速度出现在当量比为0.5附近。煤油-空气的两相RDE的实验[30]中发现爆轰波的压力随着总推进剂的质量流量增大而增加，爆轰波的压力极大值出现在当量比为1.1附近。当爆轰波传播频率的相对标准差最小时，存在一个最优的当量比值[31]。RANKIN等[32]利用OH化学发光成像技术观察RDE中的流场结构，结果表明当量比对爆轰波的传播稳定性有很大影响。随着当量比的增加，爆轰波的传播模式由单波模态变为双波模态。

目前RDE的研究以使用均相(气态-气态)燃料为主，很少有关于非均相(气态-固态或气态-液态)燃料的研究方面报道，因为非均相爆轰涉及到化学与流体动力学之间的非线性耦合以及多相之间耦合。液滴的破碎和雾化、固体颗粒热解和非均相燃烧等复杂过程难以研究。非均相爆轰和均相爆轰主要区别在于能量释放机制。在非均相爆轰中，能量释放发生在液滴或固体颗粒位置，而均相爆轰的能量释放贯穿了燃料和空气混合物，因此非均相RDE研究难度较高。在进行气固两相爆轰数值模拟时，需要建立详细的颗粒传输机理模型。

综上所述可以看出，气固两相RDE实验研究已经取得一定的进展，而数值模拟方面的研究仍然不足。为了研究气固两相RDW流场结构，笔者基于商用CFD软件ANSYS FLUENT，对非预混的煤粉-空气的RDE进行了二维数值模拟，气相采用具有体积反应的非定常黏性模型，固相采用离散相(Discrete Phase Model，DPM)模型，煤的表面燃烧反应采用动力学/扩散限制速率模型。通过调节空气流量来改变当量比，研究对爆轰波的传播特性、参数变化以及颗粒分布的影响。

1 数理化模型和计算方法

1.1 物理模型及边界条件

RDE的燃烧室通常为一个同轴圆环腔，为了简化计算，忽略燃烧室的径向方向上的参数变化，将其沿一条母线展开成一个平面二维矩形计算域，如图1所示。

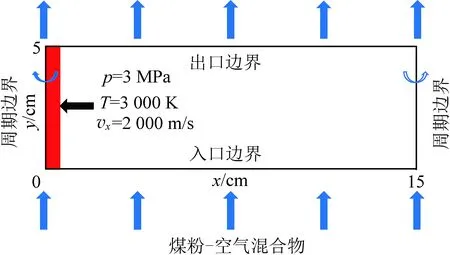
注：vx为x轴方向的速度。图1 RDE的二维模型Fig.1 Two-dimensional model of RDE

计算域的长和宽分别为15 cm和5 cm。燃烧室的左右两端为周期边界，入口边界设置为空气质量流量入口，初始化压力为0.1 MPa，来流总温为300 K。煤粉颗粒垂直入口注入燃烧室，注射温度为300 K，速度为50 m/s，质量流量为3 kg/s，颗粒直径为1.2 μm，由100%的碳组成。出口边界设置为压力出口，出口压力0.1 MPa，回流总温为300 K，DPM边界条件为逃逸。

1.2 数理化模型

笔者采用二维Navier-Stokes方程[33]和组分输运方程作为控制方程来描述旋转爆轰流场。

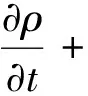
(1)

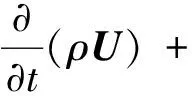
(2)

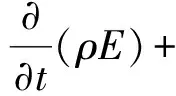
(3)

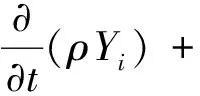
(4)

(5)

(6)

式中，μ为动力黏度；I为单位张量；h为反应物的总焓。

ANSYS FLUENT中通过在拉格朗日参考系中积分颗粒上的作用力平衡来预测离散相颗粒(或液滴或气泡)的运动轨迹。颗粒的作用力平衡方程在笛卡尔坐标系下的形式为

(7)

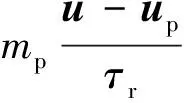
(8)

其中，dp为颗粒的直径；Re为相对雷诺数，其定义为

(9)

阻力系数Cd为

(10)

式中，a1，a2，a3为计算阻力系数，对于球形颗粒，在一定的雷诺数范围内a1，a2和a3为常数[35]。

煤粉颗粒的表面燃烧模型采用动力学/扩散控制反应速率模型[36-37]。该模型假设表面反应速率由动力学反应速率和扩散速率共同决定。扩散速率系数为

(11)

动力学反应速率R为

R=C2e-(Ep/RTp)

(12)

加权产生颗粒的燃烧反应速率为

(13)

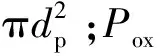
表1 煤的表面反应机理

化学反应模型采用有限速率模型，反应速率常数kf采用Arrhenius公式计算：

(14)

其中，Ar为指前因子；b为温度指数；Ea为反应活化能；T为反应物温度。各反应参数设置见表2[27,39,42]。

表2 化学反应机理

1.3 其他设置

笔者采用常温条件下煤粉颗粒为燃料，空气为氧化剂。采用密度基隐式求解器求解二维非稳态Navier-Stokes方程。湍流模型采用SSTk-ω两方程模型，物理通量采用AUSM矢通量分裂法进行分解。颗粒注射采用DPM模型，并考虑压力梯度力和虚拟质量力对颗粒的影响，颗粒运动采用球形阻力定律。

1.4 初始条件

初始时刻燃烧室内填充煤粉-空气混合物。点火时给定一块高温高压区域(T=2 000 K，p=2 MPa，vx=2 000 m/s)进行起爆，如图1红色区域所示(0≤x≤0.5 cm，0≤y≤5 cm)。模拟中发现，点火后燃烧室内会出现双波对撞现象，碰撞之后，可能导致爆轰波熄灭。为了保证爆轰波稳定传播，初始阶段将左右边界设为固壁边界，当起爆后形成的爆轰波即将达到右端边界时改为周期边界[43]。

1.5 网格独立性验证

在空气流量为68.64 kg/s、煤粉质量流量为3 kg/s的工况下，分别对0.40，0.25，0.20 mm的3种不同网格尺寸进行网格验证。图2显示在t=1 294 μs时，3种网格尺寸下RDW的压力和密度云图，可以看出不同网格尺寸下流场结构基本相同。为了进一步验证网格的无关性，表3对比了3种网格尺寸下爆轰波的高度和速度，网格尺寸为0.20 mm和0.25 mm时爆轰波的速度和高度相近，表明网格无关性验证成功。为了使模拟结果更为准确，本文采用0.20 mm网格尺寸。

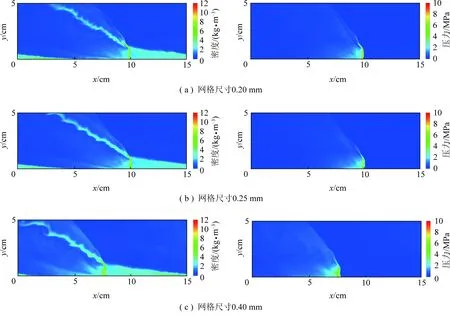
图2 不同网格尺寸的RDW的压力和密度云图Fig.2 Pressure and density contours of RDWs for different cell sizes

表3 比较不同网格尺寸下爆轰波的速度和高度

2 结果分析与讨论

为了确保数值模拟结果的可靠性，将模拟计算出的爆轰波速度与实验[17,21,25]进行比较，见表4。可以看出数值模拟和实验结果较为接近，但由于模拟采用的颗粒直径较小，加快了化学反应速率，导致爆轰波速度比实验值偏高。流场结构与BYKOVSKII等[21]通过高速摄像拍摄记录的气固两相RDW流场结构定性一致。

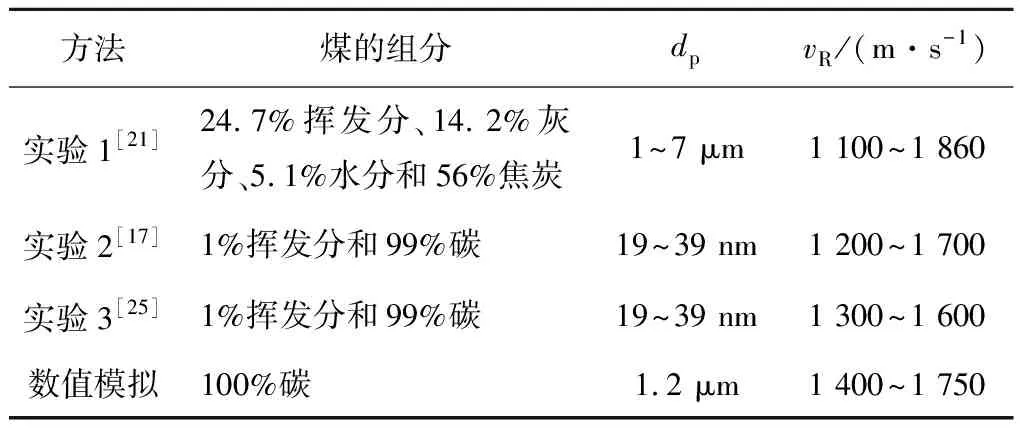
表4 煤粉-空气RDE实验和数值模拟结果

2.1 气固两相RDW的传播特性

笔者采用的模拟工况见表5，保持煤粉质量流量不变，通过调节空气流量改变当量比。空气流量为38.14，68.64，114.40 kg/s时，燃烧室内仅有1个RDW传播。空气流量为49.03 kg/s时，燃烧室内发生模态转换过程，即爆轰波数量会发生变化，同时存在单波和双波传播模态。空气流量为31.20 kg/s时，由于空气流量过低难以形成自持传播的爆轰波。以不同传播模态下的模拟结果为例，分析爆轰波的传播特性。

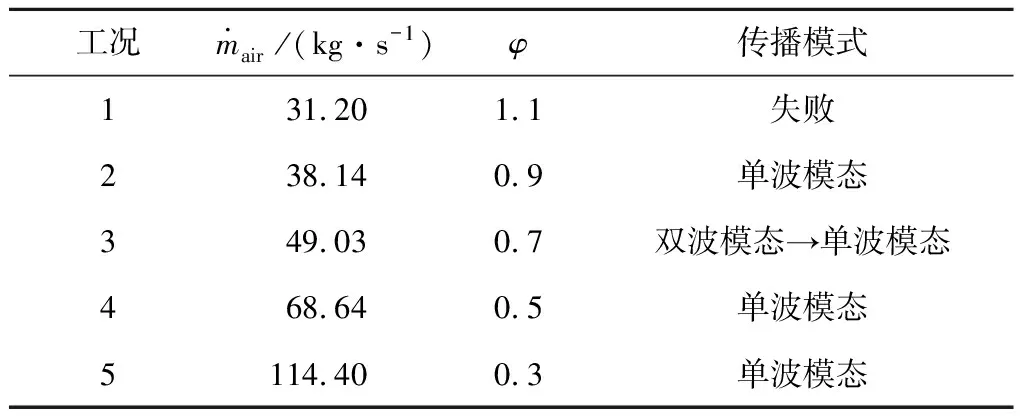
表5 模拟工况

以空气流量68.64 kg/s为例，图3分别记录空气流量为68.64 kg/s时在监测点(x=5 cm，y=0.4 cm)处温度和压力随时间的变化曲线，通过压力曲线确定RDW传播1个周期所需的时间，计算出RDW传播频率和传播速度，计算公式为

(15)

式中，f为RDW传播频率，kHz；tRDW为RDW传播1个周期所需的时间，s；L为燃烧室的x轴长度，取15 cm。

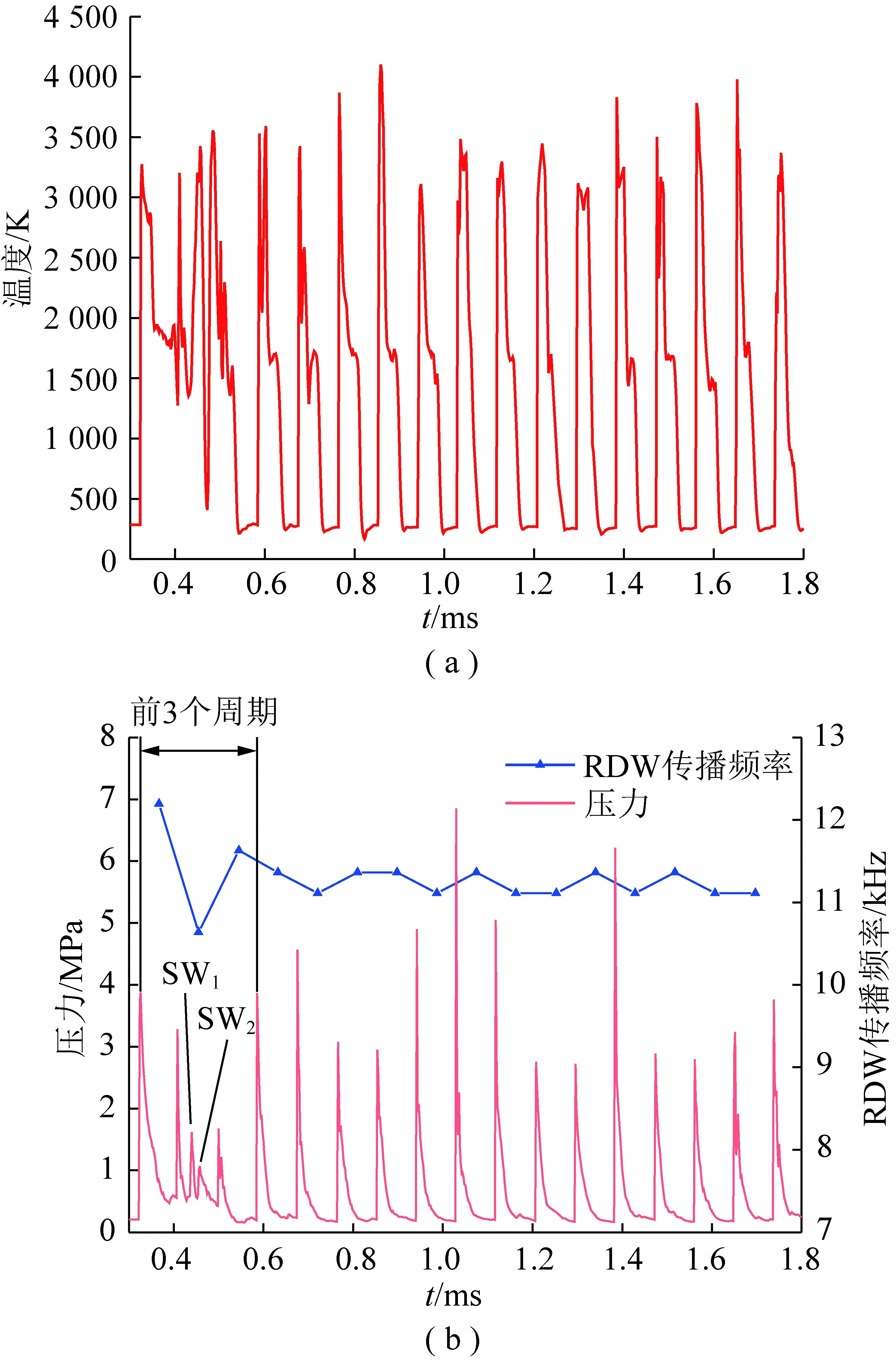
图时监测点处温度、 压力和RDW传播频率曲线Fig.3 Temperature,pressure and RDW transmission frequency traces of the monitor point for kg/s

如图3(b)所示，在爆轰波循环的前3个周期，RDW传播频率有一定波动，平均值为11.55 kHz。爆轰波第4个周期开始，RDW传播频率基本稳定(11.11～11.36 kHz)，平均值为11.23 kHz。由于横波的干扰下爆轰波面的压力峰值不断变化。根据式(15)计算出爆轰波稳定后的传播速度为1 701 m/s。RDW传播频率降低是因为初始时刻有300 μs的混合时间，使得燃料室内颗粒与空气达到较好的混合效果，因此点火后爆轰波强度较高，RDW传播频率较大。

如图3(b)所示，在t=440 μs和t=458 μs出现2处压力尖峰分别为激波SW1(Shock Wave，SW)和激波SW2，对应的压力峰值分别为1.67 MPa和1.07 MPa。

产生该现象的原因如图4，5所示，t=376 μs时，起爆后入口附近的压力衰减较慢，导致空气注射速度减小，因此爆轰波靠近右端边界时只有少量的空气注入进燃烧室。t=410～480 μs时爆轰波进入第2个循环周期时，爆轰波高度降低，波后注入燃料与高温产物直接接触，进而在入口附近发生爆燃反应形成SW1和SW2，但激波强度较低，无法演化为新的爆轰波，在t=550 μs时爆轰波第3个循环周期中激波消失，燃烧室内仅有1个RDW传播。

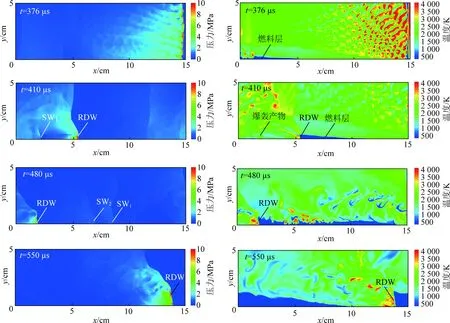
图时不同时刻的压力和温度云图Fig.4 Pressure and temperature contours at different moments for kg/s,φ=0.5

图时入口的压力和 轴向速度分布曲线Fig.5 Distribution of inlet pressure and axial velocity for

图6为空气流量49.03 kg/s，φ=0.7时不同时刻的压力和温度云图，显示了模态转变过程。高温高压条件点火起爆形成一个沿x轴正方向传播的爆轰波(Detonation Wave，DW1)。由于悬浮在空气中的煤粉颗粒可以形成具有高能成分的活性颗粒-气体混合物，能够维持以横波结构为主的爆轰波传播[20]。因此在爆轰波传播第1个周期垂直于爆轰波面横波往复运动，三波点相互碰撞，导致爆轰波面极为不规则。在t=406～440 μs内爆轰波的第2个循环周期，燃料层的填充高度很低，爆轰波高度下降，爆轰产物靠近入口附近，新注入的燃料直接与高温产物接触促使反应速率加快，进而在入口附近发生爆燃现象并在爆轰波后形成同向传播的激波(p=2 MPa，T=3 900 K)，该激波逐渐发展为较弱的爆轰波(DW2)，此时波头间距约为33.78 mm。图7(c)显示在爆轰波的前3个循环周期DW1比DW2的传播速度快，因此在t=440～730 μs内波头的间距不断扩大，导致DW1前的燃料层填充高度不断减小，爆轰波强度下降。t=906 μs时DW1的压力峰值降低到1.8 MPa，速度降低到1 508 m/s，较弱的DW1无法稳定在燃烧室内稳定传播。随着时间的推移，t=930 μs时前导激波与反应区解耦，爆轰波逐渐衰退消失。在t=1 200 μs时经过一段时间自适应调整过程[44]，最终燃烧室内形成1个沿x轴正方向传播的DW2。

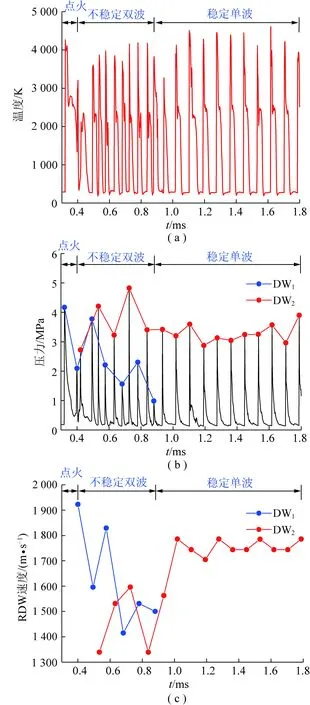
图时监测点处温度、 压力和RDW速度曲线Fig.7 Temperature,pressure and RDW velocity traces of the

双波模态转换为单波模态后，其传播特性发生显著变化。首先爆轰波的平均速度从1 460 m/s上升至1 750 m/s，且单波模态的爆轰波的高度接近于双波模态的2倍，表明双波模态下的单个爆轰波强度均小于单波模态下的爆轰波。图7(a)，(b)为模态转换对于爆轰波的温度和压力波动范围有明显影响，单波模态的压力和温度峰值波动范围明显小于双波模态，表明双波模态虽然可以传播，但每个波头强度并不恒定，爆轰波之间相互影响，导致爆轰波传播的不稳定性增加。

2.2 空气流量对气固两相RDW的影响

图8为空气流量68.64 kg/s时气固两相RDW的温度和颗粒分布云图，可以看出空气层和颗粒层没有完全重合，因为空气层和颗粒层的填充高度分别由连续相和离散相的y轴平均速度与爆轰波的速度共同决定，其中颗粒层和空气层的斜率计算公式为

(16)

其中，α为颗粒层下游边界与x轴的夹角；β为空气层下游边界与x轴的夹角(图8)；vpy为颗粒层内煤粉颗粒沿y轴的平均速度，m/s；vcy为空气层内空气沿y轴的平均速度，m/s。不同空气流量下，颗粒层和空气层的斜率见表6。

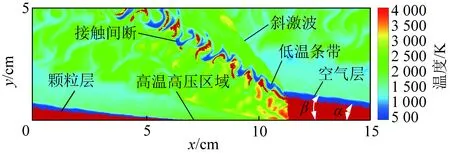
图时温度和颗粒分布云图Fig.8 Temperature contours and particle

表6 RDE各参量随空气流量变化统计

由表6可知，所有成功算例中空气层斜率均大于颗粒层的斜率，即空气层填充高度大于颗粒层填充高度。高出颗粒层的空气会穿过斜激波向下游流动，除了一小部分与接触面附近的未完全燃烧的煤粉颗粒发生爆燃反应之外，大部分被排出燃烧室，形成一条低温条带。

低温条带分隔上一轮循环的爆轰产物和本轮循环的爆轰产物，如图8所示。因此爆轰波前的当量比大于全局当量比，为了详细说明颗粒层和空气层之间的高度差对爆轰波传播的影响，引入新的参数局部当量比(Local Equivalence Ratio，φL)来表示爆轰波前的当量比，计算公式为

(17)

式中，(Air/Fuel)stoic为化学当量的空-燃比，取11.444；DPMcon为单元格中颗粒在气相中的质量浓度，kg/m3；ρg为单元格中的气相密度，kg/m3；Vcell为单元格体积，m3。

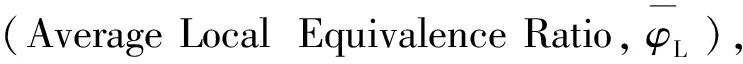
(18)

其中，A为爆轰波前的计算区域(图9)；φLcell为计算区域A中各单元格中的局部当量比；n为计算区域A中单元格的数量。计算结果见表6。式(17)，(18)中关于局部当量比和平均局部当量比的计算，仅适用于爆轰波前的反应物区，而不适用于其他区域。

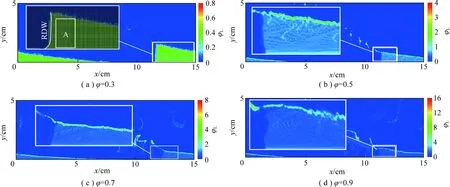
图9 不同全局当量比下局部当量比云图Fig.9 Contours of the local equivalence ratio at different global equivalence ratios

计算所得不同空气流量下爆轰波的传播特性见表6。随着空气流量的增加，爆轰波的速度和温度峰值先增大后减小，压力峰值受到空气质量流量影响逐渐增大。

空气流量为49.03 kg/s时，即全局当量比为0.7时，爆轰波的速度最大。该工况下平均局部当量比接近于1，但爆轰波扫过时部分颗粒无法完全燃烧且分布不连续的现象，如图10所示。具体原因在下节进行详细分析。全局当量比为0.9时，平均局部当量比为1.18，属于富燃工况。与全局当量比为0.7相比，燃料层的氧气含量减小，产物内未完全燃烧的颗粒数量增多且颗粒密度较大，因此爆轰波所吸收的热量减小，强度下降，如图11所示。其中，反应热指化学反应时所放出或吸收的热量。

2.3 颗粒分布和流场结构分析

在气固两相旋转爆轰过程中，气相和固相分布是研究爆轰波传播特性的关键因素之一。图12为空气流量68.64 kg/s时，稳定单波模态下燃烧室内温度、DPMcon、O2质量分数和CO2质量分数云图。其中，图12(b)中蓝色轮廓代表压力分布。根据温度和组分分布情况，将燃烧室划分为3个区域：填充区1、爆轰产物区2和爆燃产物区3。

2.3.1 填充区1

填充区1是入口燃料和氧化剂进入燃烧室所形成的三角填充区域，该区域温度较低。图9显示由于颗粒在入口和颗粒层下游边界附近堆积，导致填充区1内当量比分布极不均匀。图13显示空气流量为68.64 kg/s时入口附近颗粒的y轴注射速度为97.8 m/s，空气的y轴注射速度为182.5 m/s，颗粒y轴注射速度约为空气y轴注射速度的一半。虽然气流和颗粒之间相互作用有利于气相和固相的混合，但仍然无法在较短距离内完成充分掺混的y轴过程，因此距离入口附近颗粒无法立即分布均匀，导致颗粒堆积，局部当量比偏大。而随着颗粒和空气的y轴方向速度增大，颗粒分布逐渐趋于均匀。颗粒层下游边界局部当量比偏大是因为爆轰波后靠近入口处形成高温高压区域，高温高压区域后(x=4.15 cm)颗粒开始大量注入燃烧室，如图8，12(b)所示。此处的温度和压力分别为518 K和1.3 MPa，如图14所示。由于低于煤粉着火温度(700 K)，颗粒无法着火燃烧。但该点的压力偏高，注射的颗粒会被压缩聚集，并随着时间向下游流动，形成一条高浓度的颗粒条带，如图12(b)所示。

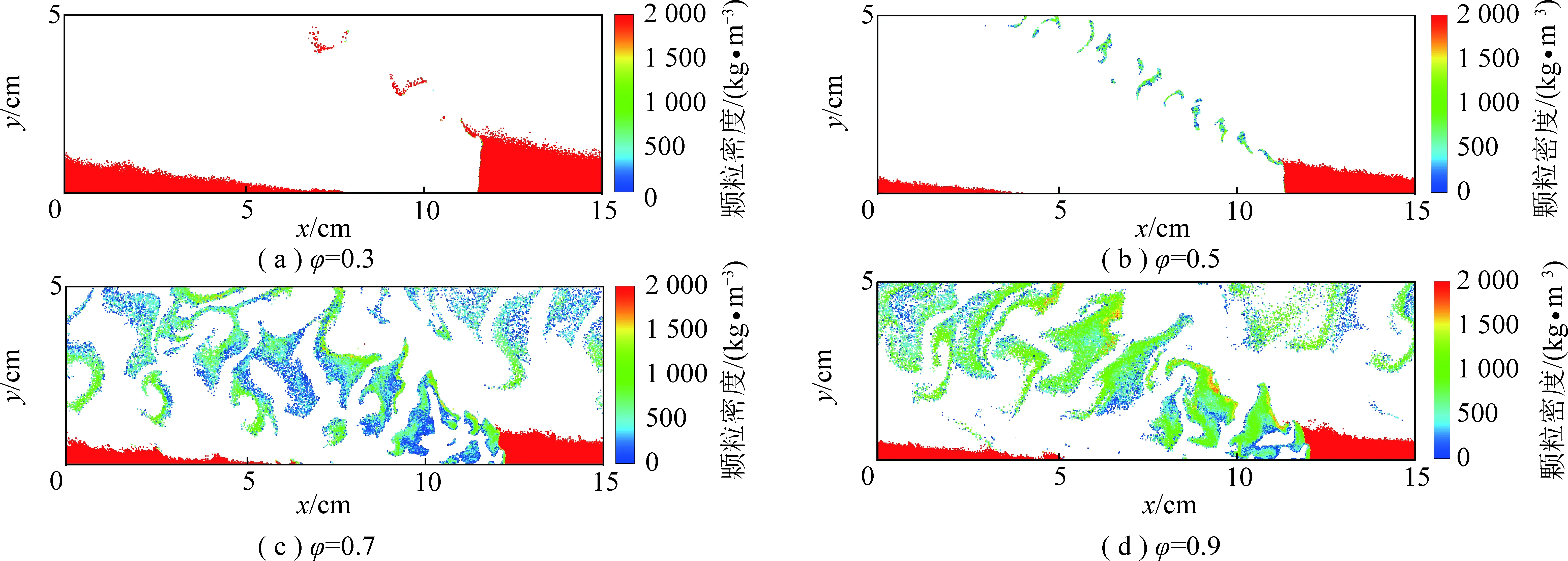
图10 不同全局当量比下的颗粒密度云图Fig.10 Contours of particle density at different global equivalence ratios

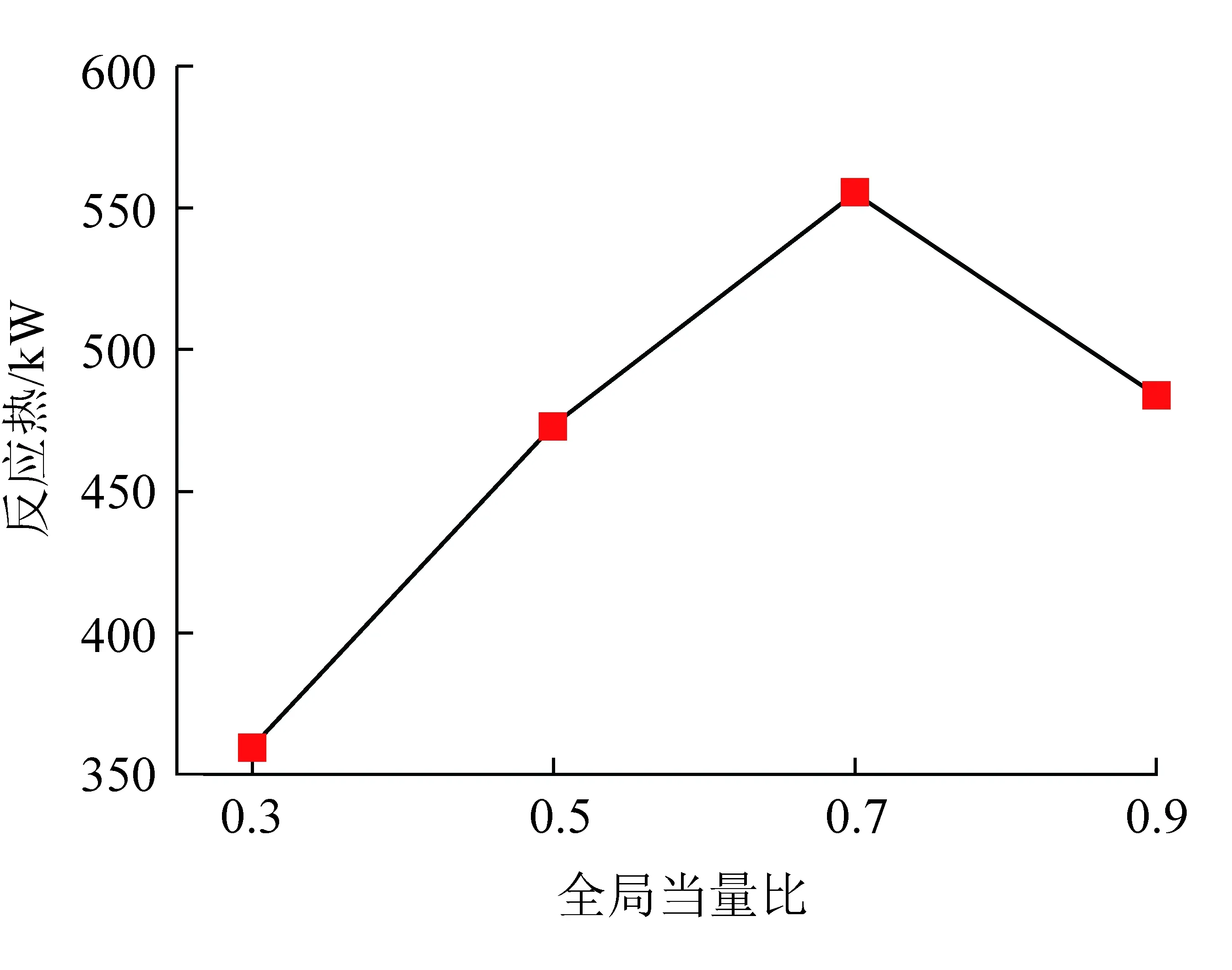
图11 t=1 800 μs时不同全局当量比下爆轰波面的反应热Fig.11 Heat of reaction of the detonation wave surface at different global equivalence ratios for t=1 800 μs

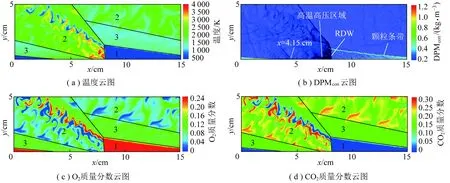
1—填充区；2—爆轰产物区；3—爆燃产物区图时燃烧室内流场分布Fig.12 Flow field distribution in the combustion chamber for kg/s

2.3.2 爆轰产物区2

爆轰产物区2是由高温产物、未完全燃烧的颗粒和剩余氧气组成。从图10可以看，全局当量比为0.7和0.9时，波后产物中存在部分未完全燃烧颗粒且颗粒的分布不连续的现象。

图15为全局当量比0.7时不同时刻的爆轰波面的O2质量分数和颗粒密度云图。图16显示在颗粒层的中间区域的局部当量比处于0.65～1.00。在爆轰波波面的横波和激波间相互作用下形成三波点结构[45]。在前导激波的作用下，气流沿x轴正方向速度增大，进而带动激波前的颗粒沿x轴正方向加速运动，引起颗粒聚集。在t=1 715 μs时，爆轰波面2个三波点相向运动，马赫激波顶点和入射激波前方存在大量颗粒堆积，导致局部当量比增大至1.14～1.42，但马赫激波端点与入射激波的接触区域呈弧形结构，该区域在沿x轴方向速度分量较小，对颗粒的加速作用较弱，故马赫激波端点的颗粒分布较为稀疏，局部当量比处于0.65～0.91。因此当爆轰波扫过时，马赫激波顶点和入射激波的后方有部分未完全燃烧的颗粒，而马赫激波端点处的颗粒完全燃烧且会有氧气剩余。在t=1 716.75 μs时，随着三波点的相向运动，三波点的间距不断减小，马赫激波波面更加突起，使得入射激波前聚集的颗粒逐渐被包裹起来，并与两侧马赫激波端点处剩余的氧气以及入射激波前的氧气发生燃烧反应。在t=1 719～1 723 μs时，入射激波前聚集的颗粒完全燃烧，燃烧后剩余的氧气在三波点碰撞后方形成氧气团，而三波点相互碰撞前方产生新的马赫激波。随着爆轰波的传播，马赫激波波面逐渐趋于平整，沿x轴方向的速度分量增大，颗粒再次发生聚集，局部当量比增大至1.08～1.33，进而爆轰波扫过部分颗粒无法完全燃烧。同理，马赫激波两端颗粒分布较为稀疏，爆轰波扫过后颗粒完全燃烧并且会有氧气剩余。

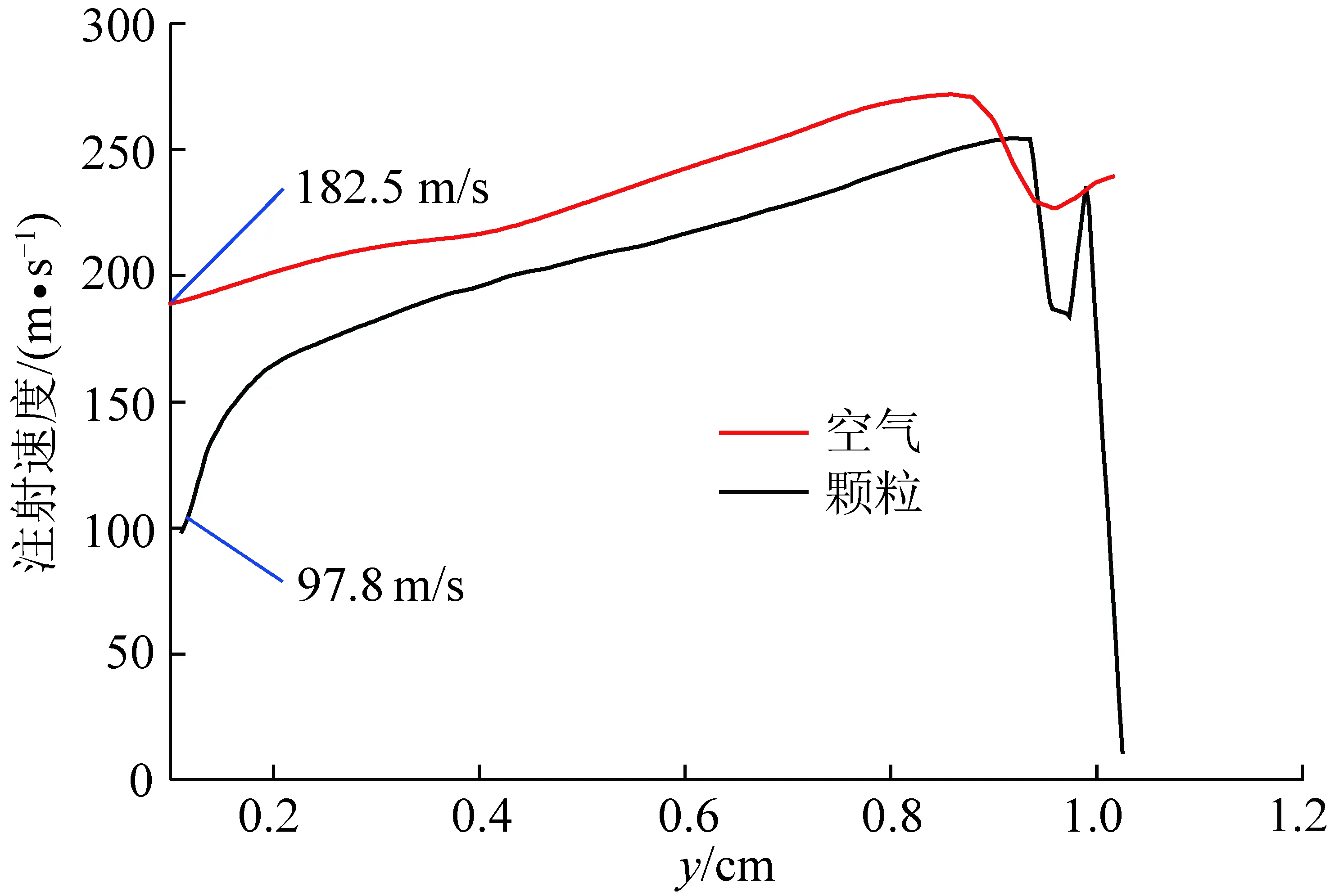
图时空气和颗粒沿x=8.1 cm 的注射速度Fig.13 Injection velocity of air and particles along x=8.1 cm

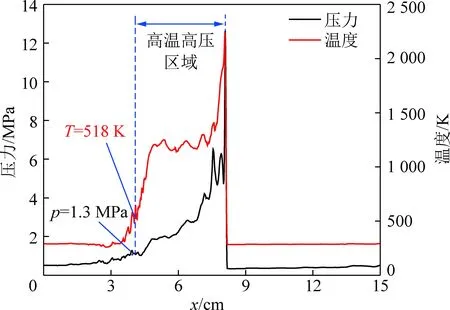
图时进口的温度和 压力分布曲线Fig.14 Distribution of temperature and pressure at

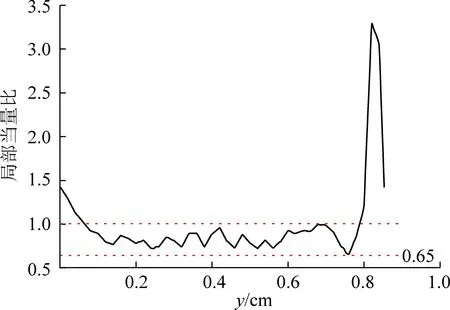
图16 φ=0.7时沿x=7.6 cm爆轰波前的局部当量比Fig.16 Local equivalence ratio before the detonation surface along x=7.6 cm for φ=0.7

因此根据上述分析，爆轰波在传播过程中横波往复运动，三波点相互碰撞，不断有马赫激波和入射激波结构重复出现。而马赫激波和入射激波的不同位置沿x轴方向速度分量大小有所不同，因此对波前颗粒加速作用也有所不同，导致爆轰波面颗粒分布不均匀，波后的产物区出现未完全燃烧的颗粒且分布不连续的现象。

2.3.3 爆燃产物区3

图12(a)，(b)以及图14显示了爆轰波后靠近入口位置形成的高压高温区域。根据热量和质量交换定律[36-37,46]，新注入的空气和颗粒部分会直接与高温高压区域接触。在对流和热传导的作用下，温度迅速升高，发生爆燃反应。剩余颗粒则仍然存在入口附近，在爆轰波扫过时通过爆轰燃烧的方式继续燃烧，如图17所示。由于高温高压区域靠近入口处，颗粒层和空气层基本重合，故该区域局部当量比近似等于全局当量比。本文模拟的成功算例均为贫燃工况，氧气量充足，与高温高压区域接触的颗粒可以完全燃烧。而爆燃所生成的产物和剩余氧气随着流场向下游流动，形成爆燃产物区3。

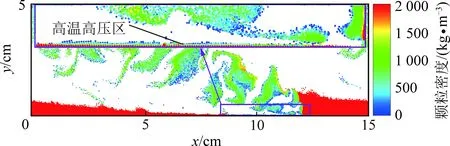
图时颗粒密度云图Fig.17 Contours of particle density kg/s

3 结 论

(1)本文计算工况中，空气流量为38.14，68.64，114.40 kg/s时，燃烧室内仅有1个RDW。空气流量为49.03 kg/s时燃烧室内存在模态转换。由于双波的传播速度不同，波头间距不断扩大，使DW1前的可燃预混层变小，爆轰波强度降低，逐渐衰减消失，最终燃烧室内形成了1个稳定传播的RDW。相对单波模态，双波模态下的爆轰波强度和稳定性都有所下降。

(2)随着空气流量从38.14 kg/s增加到114.40 kg/s 时，爆轰波的速度和温度峰值先增大后减小，而压力峰值受到空气质量流量影响逐渐增大。空气流量为49.03 kg/s时，爆轰波的速度最大。由于入口附近的颗粒注射速度低于空气注射速度，颗粒层与空气层不能完全重合，导致爆轰波前局部当量比大于全局当量比。

(3)根据燃烧室内气固两相的分布情况，爆轰波稳定时内流场可分为填充区、爆轰产物区和爆燃产物区3个区域。颗粒层入口和下游边界颗粒聚集，导致填充区内当量比分布不均匀。爆轰波面的马赫激波和入射激波沿x轴方向速度分量大小不同，对波前颗粒加速作用也有所不同，使得爆轰波面颗粒分布不均匀，波后的产物区出现未完全燃烧的颗粒且分布不连续的现象。部分新注入的颗粒和空气与爆轰波后高温高压区域直接接触燃烧生成的产物和剩余氧气形成爆燃产物区。