非均质弹塑性煤体水压致裂裂纹形态研究

邱宇超，梁卫国，李 静，贺 伟

(1.太原理工大学 矿业工程学院，山西 太原 030024；2.太原理工大学 原位改性采矿教育部重点实验室，山西 太原 030024)

煤层气作为一种清洁、高效的化石能源，在能源结构调整中一直占据着重要地位。为提高煤层气的采出量，目前主要使用水力压裂的方法对煤储层进行增渗改造，复杂的水力裂缝可有效提高煤储层的渗透率。准确模拟出工程尺度下天然煤储层在水力压裂后形成的裂缝形态，对施工工艺的改进和储层开采价值的评估有重要意义。针对煤体水力压裂的数值模拟，传统方法多将脆性材料的断裂准则作为水力裂缝的扩展判据[1-2]，但煤体是一种弹塑性材料，且低脆性储层中强度的非均质性是复杂缝网形成的关键因素[3]，如何对天然煤储层经水力压裂后的复杂缝网形态进行模拟成为目前研究的重要内容。

GRIFFITH[4]最早将二维裂缝缺陷视为椭圆形，并通过能量法给出了二维平面应变解的最简形式。随后SNEDDON[5]将其扩展到饼状的半无限裂缝，PKN模型[6]和KGD模型[7]就是基于这一线弹性理论推导出来的。SETTARI[8]在PKN模型的基础上提出了拟三维模型(P3D)，模型考虑了裂缝高度的变化，以上模型均适用于脆性材料。脆性材料中的裂纹扩展判据主要有最大拉应力准则[9]、最小应变能密度准则[10]和最大能量释放率准则[11]，然而这些方法不能准确描述韧性材料的断裂过程。为消除线弹性应力解在裂缝尖端存在的奇异性，BARRENBLATT[12-13]和DUGDALE[14]提出了黏聚型模型(CZM)的概念。SHET等[15]在黏聚型裂纹模型的基础上，对裂纹扩展过程中的能量变化进行详细描述，对韧性材料裂纹扩展中的部分物理现象作出解释。为阐明弹塑性煤体中水力裂缝的扩展机理，梁卫国等[16]将黏聚型模型引入到水力压裂当中，建立了煤体断裂过程区的黏聚型裂纹本构关系，对弹塑性煤体中水力裂缝的扩展作出了更准确的描述。

为预测天然煤储层在水力压裂后的裂缝形态，需要使用数值模拟方法，对水力压裂中复杂的流固耦合问题进行计算模拟[17]。目前用于水力压裂的数值模拟方法较多，其中边界元、扩展有限元和离散元的应用较为广泛。边界元(BEM)是基于位移不连续法(DDM)提出的，由CROUCH等[18]引入到固体物质的模拟当中，随后REZAEI等[19]提出同时求解连续性方程和泊松方程的方法，来计算裂缝内运动流体的真实压力，但是边界元法目前仍无法模拟岩石基质内的渗流。扩展有限元(XFEM)不需要对模型网络进行重划分，就可以模拟裂纹的扩展过程[20-21]，实现了流固耦合计算，但是不能很好模拟水力裂缝的分岔与融合[22]。离散元(DEM)是针对岩石的变形、损伤、破裂和稳定性问题提出的[23]，最早由PINE等[24]应用于岩体的流固耦合问题当中。目前的商用离散元软件(如UDEC)可以较好模拟节理、裂隙，但传统离散元依旧无法模拟岩体的基质破裂。键合粒子模型(BPM)由CUNDALL[25-26]提出，目前应用该方法的商业软件(如PFC)可以模拟岩体的基质破裂，又可以进行流固耦合计算，但是颗粒间力学参数与岩石宏观参数存在差异，且球形颗粒难以反映有棱角的煤岩颗粒。为解决上述问题，MUNJIZA[27]提出了有限离散元(FDEM)方法。该方法既能对连续介质的应力状态进行精确计算，又能捕捉离散块体间的相互作用，可以模拟连续完整介质的破裂，也可以模拟天然节理的张开，目前有限离散元方法已被应用到水力压裂的模拟当中[28-30]。

笔者使用有限离散元方法，在弹性基质单元间嵌入基于B-K混合能量准则[31]的黏聚型单元，用于模拟天然状态下弹塑性煤体中水力裂缝的扩展过程。以Weibull分布密度函数为依据，采用Monte Carlo方法对黏聚型单元的强度与断裂能进行随机赋值[32]，来描述天然状态下煤体的非均质性。笔者在模拟水力裂缝的裂隙流时，根据裂缝开度和损伤程度变化，对Darcy流与Poiseuille流之间的相互转化加以考虑，并对煤层的基质渗流进行流固耦合计算，得到天然状态下不同非均质程度的煤层，在单簇射孔水力压裂后的裂缝扩展形态。该研究成果对煤储层水力压裂复杂缝网的形成、储层增渗改造施工工艺的改进以及储层开采价值的评估具有较为重要的指导意义。

1 黏聚型单元控制方程

FDEM方法的基本思路是在已划分好的基质单元间嵌入黏聚型单元(图1)，2种单元的耦合可对连续体的变形进行模拟，固体基质单元用于模拟多孔介质；黏聚型单元用于模拟弹塑性断裂。黏聚型单元的失效即为裂纹的扩展，通过给黏聚型单元赋予不同的强度来表征煤层中的天然弱面，可同时对煤层中天然节理的张开和完整块体的破裂进行模拟，带孔压自由度的黏聚型单元，不仅可以模拟单元内流体的切向流qt与法向流qn，还可以模拟单元破裂前后不同流态的转化，适用于模拟水力裂缝的裂隙流。

图1 FDEM中的单元布置与相互作用Fig.1 Unit arrangement and interaction in FDEM

1.1 弹塑性断裂本构方程

在黏聚型单元的本构模型构建中，使用二次名义应力准则作为单元的初始损伤判据，具体表达式为

(1)

其中，〈σn〉为正应力，拉应力时取正值，压应力时取0，与张开型(Ⅰ型)断裂相对应；σs和σt分别为2个正交方向剪应力，与滑开型(Ⅱ型)、撕开型(Ⅲ型)断裂相对应；Nmax为煤体抗拉强度；Smax和Tmax分别为煤体2个正交方向的抗剪强度，在煤岩体中一般认为二者相等。当单元应力状态满足式(1)时，单元开始发生损伤，随着分离位移的继续增大，单元刚度与承载力均不断下降，最终完全失效。通过引入损伤变量D来描述单元损伤演化过程，单元的实际应力状态为

(2)

式中，D为损伤变量，在初始损伤到完全损伤的过程中从0变化到1；¯σn,¯σs,¯σt为无损伤状态下，根据分离位移预测的当前应变所对应的应力峰值。为描述黏聚型单元损伤变量D，随法向—切向组合变形的演化过程，引入有效位移δm[33]的概念，其定义为

(3)

式中，〈δn〉为法向位移；δs，δt为2个正交方向的切向位移。

图2 黏聚型单元的本构关系曲线Fig.2 Constitutive relation curves of cohesive elements

混合断裂能Gc随着Ⅰ，Ⅱ型断裂形式混合比例的不同而发生变化，本文采用基于B-K准则的混合断裂能模型，B-K准则适用于Ⅱ,Ⅲ型剪切裂纹断裂能相近的材料，具体表达式为

(4)

(5)

(6)

1.2 裂隙流流态转化方程

黏聚型单元中流体的切向流动会随单元的损伤而发生变化，随着损伤程度的增加，切向流从未损伤状态下的Darcy渗流转化为完全损伤后的Poiseuille管道流。需要对2种流态之间的相互转化进行定义，主要考虑损伤变量与裂缝开度两方面影响因素，具体方程为

(7)

(8)

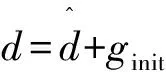
黏聚型单元中流体的法向流动可以通过滤失系数进行描述，这些系数定义了黏聚型单元的中间节点与其相邻曲面节点之间的流量-压力关系。流体滤失系数即单元壁面上单位厚度材料的渗透性，具体表达式为

qn=cn(pi-pw)

(9)

其中，qn为法向流流量；cn为法向滤失系数；pi为单元中面流体压力；pw为单元壁面孔隙压力。当黏聚型单元完全破坏时，法向滤失系数应近似等于基质单元渗透系数与压裂液比重的比值。

2 Ⅰ/Ⅱ型混合断裂试验研究

由1.1节可知混合断裂能Gc是弹塑性断裂本构方程的主要控制因素，本节试验主要分为两部分。第1部分为预制不同倾角裂缝的SCB试验，对煤体的混合断裂能进行测量，按照B-K准则对试验结果进行参数拟合。第2部分为真三轴围压状态下的水力压裂试验，根据GB/T 4161—2007《金属材料平面应变断裂韧度KIC试验方法》中的矩形紧凑拉伸试件尺寸标准对煤样进行加工，在煤试样外部包裹环氧树脂制成100 mm×100 mm×100 mm的立方体试件并进行水力压裂试验。

对水力压裂试验进行数值模拟，将模拟结果与试验结果进行对比，验证基于B-K混合断裂能准则的黏聚型裂纹本构方程的适用性，以及FDEM方法的准确性。

2.1 基于SCB试验的混合断裂能测试

在考虑了T应力的情况下，SCB试验中试件的尺寸效应可以忽略。采用数控机床金刚砂线切割机制备如图3所示的煤样试件(θ为裂纹偏转扩展的偏转角)，其尺寸为R=25 mm、a/R=0.35(a为预制裂缝长度；R为时间半径)、厚度20 mm、预制裂缝倾角β分别为0°，20°，30°，40°，45°和54°。不同倾角对应不同比例的拉剪混合状态，其中0°对应着纯Ⅰ型断裂形式，54°对应纯Ⅱ型断裂形式[34]。试验过程中采用位移加载的方法，加载速率为0.02 mm/min，下侧2个加载点间隔12.5 mm。根据不同倾角试件破坏时的峰值荷载，计算出混合断裂形式下煤样的断裂韧性。AYATOLLAHI[34]详细给出特征尺寸a/R=0.35，S/R=0.5(S为下侧2个载加点距离的一半)的试件，不同预制裂缝倾角情况下Ⅰ型断裂韧性KⅠf，Ⅱ型断裂韧性KⅡf和T应力的计算方法与相关参数。

SCB试验加载后的裂缝扩展形态如图4所示，预制裂缝倾角较小时扩展裂缝较为光滑以Ⅰ型断裂为主，随着倾角的不断增大扩展裂缝变得粗糙，这表明断裂形式由Ⅰ型向着Ⅱ型逐渐转化。倾角为54°的试件加载后扩展裂缝出现了分层剥离现象，这表明裂缝为剪切破坏，证明了其对应着纯Ⅱ型断裂形式。

图3 SCB试验试件与参数Fig.3 SCB test specimens and parameters

线弹性断裂力学中，纯Ⅰ型或纯Ⅱ型断裂形式所对应的断裂能与断裂韧性有如下关系：

G=K2/E′

(10)

其中，G为断裂能；K为断裂韧性；E′=E(平面应力状态)，E′=E/(1-ν2)(平面应变状态)，E为弹性模量，ν为泊松比。裂纹扩展中的能量释放率就是裂纹扩展单位长度所需要的能量，即断裂能，CHENG给出考虑T应力修正的能量释放率准则[35]，该准则可计算出混合断裂形式下，预制裂缝尖端萌生出倾角为θ的微裂纹时的能量释放率，即为本试验中不同混合状态下裂纹扩展的临界断裂能，其具体表达式为

(11)

图4 SCB试验加载后裂缝形态Fig.4 Crack morphology after loading in SCB test

图5 煤体的混合模式断裂能Fig.5 Mixed mode fracture energy of coal

(12)

2.2 原位条件下水力裂缝偏转扩展试验

图6 环氧树脂包裹煤样试件Fig.6 Epoxy coated coal sample

试验所用试件(图6)内部煤样尺寸为75 mm×60 mm×25 mm，预制裂缝长度为25 mm，裂缝尖端和开口处贴有应变片，在煤样外部浇筑环氧树脂制成100 mm立方体试件，煤样预制裂缝平面与主应力方向成一定倾角α(图7)，共制作了0°，15°和30°三种不同倾角的试件。在浇筑前对预制裂缝及应变片分别进行处理，防止环氧树脂进入裂缝凝固，局部隔离环氧树脂的黏结作用，保证应变片准确测量煤样的变形。试件浇筑完成后，在试件上钻出一直达煤样预制裂缝的圆孔，放入注液管并用环氧树脂胶固定。

图7 不同煤样倾角的包裹试件Fig.7 Wrapped specimens with different inclination angles of coal samples

采用太原理工大学原位改性采矿重点实验室自主研制的TCHFSM-I真三轴压裂渗流模拟装置[37]进行水力压裂试验，试验过程中围压设置为σ1=10 MPa，σ2=8 MPa，σ3=6 MPa，注液流量为4 mL/min，压裂流体通过注液管直接进入煤样的预制裂缝，持续的流体注入会驱动裂缝扩展。不同倾角的试件对应着不同的断裂形式，0°倾角试件可对弹塑性煤体中纯Ⅰ型断裂裂缝的扩展进行研究，15°和30°倾角试件为Ⅰ/Ⅱ型混合断裂，可对裂缝的偏转扩展进行研究。

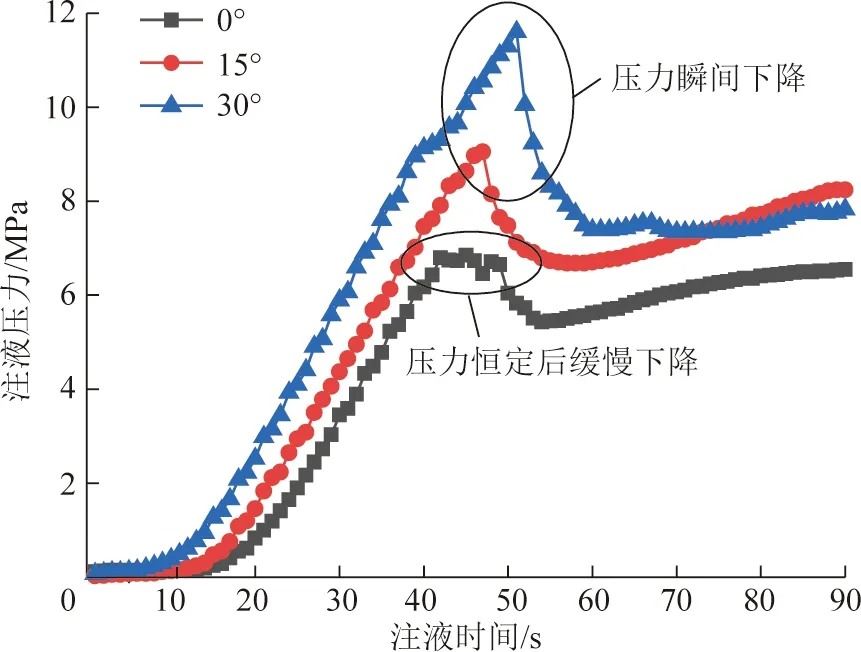
图8 不同倾角试件注液压力曲线Fig.8 Injection pressures curves of specimens with different inclination angles

试验过程中的注液压力曲线如图8所示，注液初期90 s的试验数据，包含了煤样的裂缝起裂和扩展过程。从图8不难看出，煤体的纯Ⅰ型裂纹扩展呈现出韧性断裂，注液压力稳定驱动裂纹扩展了一段时间后才开始下降；而在Ⅰ/Ⅱ型混合断裂情况下，随着倾角的增大(剪应力占比提高)裂缝起裂需要更高的注液压力，且混合断裂状态下，注液压力在达到起裂压力后迅速下降。15°倾角试件的水力裂缝形态如图9中的蓝色曲线所示，试验过程中水力裂缝在扩展到煤样边界后，流体会继续进入环氧树脂与煤样的交界面导致界面开裂。煤-环氧树脂交界面颜色较浅的为分离部分，颜色较深的为黏结部分，2者之间的分界线即为水力裂缝位置。由于试验所用煤试样存在天然弱面，水力裂缝再扩展到弱面时终止，未能完全扩展到煤样边界。

图9 水力压裂裂缝形态对比验证Fig.9 Comparison and verification of hydraulic fracturing fracture morphology

对15°倾角试件的水力压裂试验进行同条件数值模拟，模拟中所用材料参数与试验中所用煤样的力学参数一致，且使用SCB试验中基于B-K准则的混合断裂能，结果如图9所示。图9中部的灰色矩形为煤样、红线为水力裂缝，将其与试验结果绘制在一起进行对比，可以看出2者的裂缝形态有着较高的吻合度。

比较该数值模拟与水力压裂试验中的注液压力—时间曲线、裂缝开口处以及裂缝尖端处的张开位移(位移模拟结果的数据提取位置与试验中应变片中轴线的位置相同)，结果如图10所示，可以看出，数值模拟中的注液压力和裂缝张开位移的峰前以及峰值处曲线，与试验结果有较高的拟合度，但峰后曲线存在一定差异，特别是裂缝尖端张开位移的峰后曲线更为显著。导致上述差异的原因，是因为水力裂缝扩展过程中，裂纹扩展路径上的完整煤体受到环氧树脂的黏结作用，阻碍了裂缝进一步张开，导致裂缝稳定扩展时需要更高的注液压力，且裂缝尖端处的张开位移在峰后也下降得较多，而数值模拟当中并未考虑环氧树脂的黏结作用。

图10 注液压力和裂缝张开位移-时程曲线Fig.10 Injection pressure and displacement-time curves of crack opening

3 非均质弹塑性煤体裂纹扩展模拟

本节考虑了天然状态下煤体强度和断裂能的非均质性，即模型中黏聚型单元的抗拉、抗剪强度和对应的混合断裂能在空间上是非均质的。模拟出不同非均质程度弹塑性煤体在单簇射孔情况下，水力压裂作业后形成的裂缝形态、孔隙压力分布和注液压力-时程曲线，并对比分析其中存在的特点与差异。

3.1 煤体的非均质性

本研究对煤储层非均质性的描述，不考虑Ⅳ级以上结构面[38]，也不考虑微观(10-3m)孔裂隙，仅考虑煤层在细观(10-1m)尺度上强度的非均质性，该尺度上的非均质性可由室内标准尺寸力学试验确定。张春会等[39]对煤层进行大量钻孔取样，制成标准试样进行力学试验，试验的统计结果表明：煤的抗拉、压强度均服从Weibull分布，且抗拉强度的统计参数m(即非均质系数)为4.7。

FDEM方法中的宏观(101m)煤储层模型，由众多模拟细观煤体断裂性质的黏聚型单元组成，按照Weibull分布对单元强度和混合断裂能随机赋予，即可描述天然状态下煤储层的非均质性。Weibull分布的密度函数表达式如下：

(13)

其中，a为煤体强度、断裂能的统计平均值(已由2.1节中的试验获得)；φ(x)为黏聚型单元强度、断裂能等于x的概率密度；m为非均质度系数，描述煤储层强度的非均质程度。m越大表示储层强度越均质，每个细观单元的强度值越接近于统计平均值；m越小表示储层强度越离散，模型中所有细观单元强度的方差越大。

FDEM方法有较强的网络依赖性，需要考虑单元力学参数的尺寸效应，合理模拟不同尺度下岩石的力学性质。孙晓璇[40]提出了广义代表体积单元(GRVE)的概念，单元表征了岩石细观尺度上的力学性质，并给出了模拟中单元所用力学参数随单元尺寸的变化规律。GRVE适用精度可以达到1∶1 000，即宏观模型尺寸最大可为细观单元尺寸的1 000倍，超过该范围后单元的尺寸效应和非均质性均不能采用同一理论进行描述。如以室内标准试验试件尺寸为依据，确定模型在细观尺度下的尺寸效应与非均质性，则宏观模型尺寸最大可为50 m。超过该尺度后，煤储层的强度非均质性被弱化，煤储层非均质性描述的主要考虑因素，转变为Ⅳ级以上结构面和断层。

3.2 数值模拟模型

图11 单簇射孔煤储层模型Fig.11 Single cluster perforated coal reservoir model

水力压裂模拟中，煤层可以视为一个半无限体模型，这里取煤层的水平截面为研究对象，进行二维状态下的水力压裂模拟。模型(图11中，σH为最大水平主应力；σh为最小水平主应力；σv为垂直应力)中地层尺寸为15 m×15 m，钻井方向平行于最小水平主应力方向，地层正中间为4组射孔，射孔方向平行于最大水平主应力方向，射孔间隔0.25 m、射孔长度0.3 m。在实际的三维状态下，一组射孔会沿着垂直于水平井的4个不同方向进行，目的是使煤体形成初始的破裂面，降低后续压裂作业过程中的起裂压力，二维情况下破裂面为一条贯通水平钻井两侧煤体的直线。本模型共有4个相互独立的初始破裂面，采用矩形单元对模型进行单元网络划分，单元尺寸不应大于断裂过程区(FPZ)长度[41]，在划分好的基质单元间嵌入零厚度的黏聚型单元，最终模型中包含295 015 个待求解单元，其中基质单元98 705个、黏聚型单元196 310个。

模拟所使用的材料参数以及地应力条件见表1，

表1 数值模拟中所用材料参数

根据抗拉、抗剪强度期望值以及混合断裂能期望值，按照Weibull分布对模型中的黏聚型单元进行随机赋值，共计算了9个不同非均质程度的模型，非均质度系数m分别等于1.3，1.5，1.8，2.0，3.0，5.0，12.0和30.0以及完全均质状态。模型四周的边界条件为固定法向位移，地应力通过预应力平衡的方法施加到单元上，地层初始孔隙压力为0.1 MPa。压裂液注入方式为恒流注入，为避免初始高速流体的冲击作用，保证初始注入状态时平衡方程求解的收敛性，注液开始的1 s内流量从0升高到目标值。

3.3 裂纹形态规律

图12为压裂作业50 s时数值模拟的裂缝形态和煤层孔隙压力，为方便对比不同非均质程度下结果的差异，煤层的孔隙压力上限阈值设为12 MPa，云图中超过12 MPa的部分均为红色。从图12可以看出，当煤储层非均质程度较高时，在水平井两侧只会形成单一的长直裂缝，且形成长裂缝的射孔是随机的，此情况下煤层的孔隙压力较低。随着非均质度系数的增大，裂缝出现了分叉扩展的现象，分支裂纹增加，且裂缝发生频繁偏转，当非均质度系数m=2时，裂缝形态最为复杂。随着非均质程度的进一步下降，裂缝会向着对称的双翼曲线裂缝转化，只有边侧射孔会扩展形成裂缝。

图12 不同非均质度煤储层水力压裂后地层孔隙压力Fig.12 Formation pore pressure after hydraulic fracturing in coal reservoir with different homogeneity

随着煤层非均质度的下降，水力裂缝稳定扩展时需要更高的注液压力，煤层的孔隙压力也会随之升高。云图中裂缝尖端处的孔隙压力为0，这是因为裂缝扩展过程中尖端开裂瞬间会形成低压真空区。图12中裂缝附近的孔隙压力会发生突变，这是因为裂缝扩展过程中的应力集中，会导致裂缝壁面部分范围内的黏聚带单元发生损伤，由于设置了Darcy渗流和Poiseuille裂隙流之间的转化，黏聚带单元发生损伤后，其渗透率会明显提高，孔隙压力也会快速升高。

从模拟中的注液压力-时间曲线(图13)得到：当非均质度系数m<2.0时，曲线并没有明显的压力峰，而是在注液初期有一个较为平缓的突起，且整个压裂过程中的注液压力均较低。当m=2.0～5.0时，曲线有着明显的压力峰，达到起裂压力后注液压力迅速下降，与m<2.0的煤层相比，该非均质程度的煤层中，裂缝稳定扩展时的注液压力较高。随着非均质程度的进一步下降，注液初期的压力峰逐渐消失，又变为较平缓的突起，整个压裂过程中的注液压力均较高。随着水力裂缝的不断延伸，注液压力的主要影响因素，从煤体的断裂韧性转换为压裂液黏度，这里只进行了前50 s的模拟，后续随着压裂作业的进一步进行，压裂液运移距离增加且摩阻力增大，注液压力将会不断升高。

图13 不同非均质度煤储层水力压裂过程中注液 压力-时间曲线Fig.13 Injection pressure-time history curves in hydraulic fracturing of coal reservoir with different homogeneity

将注液压力-时程曲线中的压力峰值定义为起裂压力pc，绘制起裂压力-非均质度系数曲线如图14所示，对其进行参数拟合便可以得到pc关于m变化的函数表达式为

pc=-44.02e-m/0.79+22.19

(14)

图14 起裂压力-非均质度系数曲线Fig.14 Crack initiation pressure-homogeneity coefficient curve

从图14可以看出，当m<3.0时起裂压力随着非均质度系数的增大而快速升高，拟合函数式表明该阶段的起裂压力呈指数变化，当m>3.0时煤层的起裂压力不再发生明显变化，压力稳定在22 MPa左右。

将模拟结果中开度大于0.2 mm的裂缝提取出来，并进行二次后处理，得到不同非均质程度煤层水力压裂形成的裂缝形态,如图15所示，由图15可知非均质度系数m=1.8～3.0的煤层，水力裂缝会出现明显的分叉现象，并形成分支偏转裂纹；当m=2.0时分支裂纹延伸距离最远，形成较为复杂的缝网；从m=3.0开始，裂缝的复杂程度明显下降，分支裂纹的延伸距离也会减小；在m>5.0后分支裂纹的数量明显减少，水力压裂只会使边侧射孔延伸形成2条相互独立的曲线裂缝。

LI等的研究表明[42]，煤岩裂缝只有在拉剪混合应力状态下，才可能出现分叉扩展现象。从模拟结果可以看出，完全均质煤储层中，煤体强度均匀分布，水力裂缝由Ⅰ型断裂主导，裂缝只会沿着垂直于最小主应力的方向扩展。非均质煤储层中，存在方向不定的天然弱面，水力裂缝扩展会遇到弱面，弱面开启后水力裂缝尖端处于拉剪混合应力状态下，导致水力裂缝分叉扩展或偏转扩展进而形成复杂缝网，因此天然弱面是形成复杂缝网的一个关键因素。非均质度系数m越小，煤储层的弱面越多，水力裂缝扩展过程中的分叉概率越高，但模拟结果表明当弱面(低强度单元)密度增加到一定程度后，水力裂缝的形态会随着弱面的继续增多而变得单一，这说明只有特定分布密度的弱面，才会使煤储层在水力压裂后形成复杂缝网。

4 讨 论

本文同时考虑了煤体的弹塑性与非均质性，对天然煤体在水力压裂后的裂纹形态进行模拟。模拟结果表明非均质性对水力裂缝的形态有至关重要的影响，且只有非均质度系数m=2.0～5.0的煤层注液压力曲线会出现压力峰，符合工程中实测的注液压力曲线。这说明工程尺度下的水力压裂数值模拟，不仅要从断裂机理出发对储层本构模型进行准确构建，还有必要考虑储层的非均质性，这样才能模拟出水力压裂形成缝网的真实形态，为施工工艺改进和储层开采价值评估提供参考。

图15 不同非均质度煤储层水力压裂后裂缝形态Fig.15 Fracture morphology of coal reservoir with different homogeneity after hydraulic fracturing

由本研究可知，非均质度系数m=1.8～3.0的煤储层更适合进行水力压裂改造，改造后形成的复杂导流通道可有效提高煤储层渗透率。文献[35]中实测的某煤储层的强度非均质度系数m为4.7，提高该储层的非均质程度可以提高水力压裂后的改造效果。SCCO2的压裂和萃取作用可提高煤层非均质程度，控制SCCO2的注入量和作用时间，使部分区域内煤体的非均质度系数降低到2左右，再进行水力压裂作业可使该区域内形成复杂裂缝，2种工艺的交替使用可使煤储层形成大面积的复杂缝网。

国内煤层气资源主要赋存于深部煤体，地质条件对其产能的约束显著[43]，深部煤体随着埋深的增加，孔隙率下降、节理裂隙减少、塑性增强、强度增加，这些物理力学性质的改变致使水力压裂施工需要远高于地应力的注液压力，制约了深部煤储层的增渗改造；受构造演化史、热演化史以及煤心矿物成分影响，深部煤体仍具有一定的强度非均质性，随着煤储层埋深的增加煤体完整性逐渐提高，致使非均质性对人工缝网形态的影响越发显著。一般的煤层气“甜点区”预测主要以煤储层厚度、吨煤含气量和节理发育程度为依据[44]，未充分考虑煤体的非均质性，本研究结果可为“甜点区”预测增加参考项，根据非均质性对深部煤储层进行筛选，或对较均质煤储层进行人为干涉(SCCO2或微生物作用等)提高其非均质性，均有助于后续的压裂施工形成复杂缝网，且非均质度的提高有利于降低起裂压力。

5 结 论

(1)在已经建立的煤体弹塑性本构基础上，结合煤体实际物理力学特性，引入煤体强度与断裂能的非均质性，建立了基于B-K混合断裂能准则的黏聚型裂纹扩展本构模型，并进行了复杂应力状态下非均质弹塑性煤体中水力裂缝偏转扩展的模拟。

(2)采用环氧树脂包裹含预制裂缝煤试样的立方体试件，对复杂应力状态下水力裂缝的扩展进行了可视化试验研究；试验中纯Ⅰ型断裂的注液压力曲线存在明显的稳压驱动阶段，证明弹塑性煤体具有典型的韧性破坏特征；Ⅰ/Ⅱ型混合断裂的注液压力曲线则存在明显的起裂压力，且剪力占比越大起裂压力越高。

(3)宏观尺度水力压裂模拟结果表明：非均质度系数m<1.8的煤层经水力压裂后只会形成单条的长直裂缝；m=1.8～3.0的煤层水力压裂后会形成较为复杂的裂缝，其中m=2.0的煤层形成的缝网最复杂，分支裂缝延伸的距离最远；m>3.0的煤层中水力裂缝的分叉数量明显下降，当m继续增大超过5.0后水力压裂只会形成对称双翼曲线裂缝。