基于多场耦合能量和熵产分析的矿用双盘式磁力耦合器参数多目标优化
2022-11-11郭永存李德永
王 爽,郭永存,李德永,程 刚,马 鑫
(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001;2.安徽理工大学 机械工程学院,安徽 淮南 232001)
双盘式磁力耦合器是一种采用非接触方式传递动力的新型调速装置[1],具有轻载启动、过载保护、隔离振动、零泄露、节能环保等特性[2],与传统的机械联轴器、液力耦合器等传动装置相比,磁力耦合器的调速性能更高效、大功率传动更可靠,恶劣环境适应性更强、运行成本更低,因此适用于煤矿恶劣的工作环境[3]。近年来已逐渐成为矿山机械装备传动系统的重要组成部分[4]。
电磁-温度-应力耦合能量作用是一个相当复杂的问题,已成为磁力耦合领域的热点课题之一[5]。双盘式磁力耦合器运转时,由于导体铜盘内电阻的存在,铜盘内生成的感应涡流会有一部分转化成热能,造成磁力耦合器内的温度升高。当温升高达一定值时,会导致永磁材料的剩余磁感应强度快速下降,从而磁力耦合器所能传递的力矩降低,影响其正常工作[6]。BADICS Z等[7]针对非线性单向耦合电磁热问题,提出一种自适应时间积分算法,通过对感应淬火问题和绝缘栅双极晶体管测试模块的热分析,说明了该算法的有效性;MAKNI Z等[8]采用耦合的电磁-热模型分析了永磁电机,降低了设计过程的耗时并提高可靠性;KIM D S等[9]提出了一种电磁-热耦合三维有限元分析法,测量了实际模型的电流波形和温度变化,根据模型的形状和电流波形进行了有限元建模;ECKERT P R等[10]提出了一种考虑几何和温度约束的热耦合和电磁耦合的线性致动器的设计方法,该方法使力密度最大,力纹波最小;ELKALSH A等[11]提出了一个耦合的电磁-热模型,并通过非线性和色散等离子体材料模型耦合,分析了耦合电磁热模型的稳定性和精确性。国内学者也对磁热耦合方法开展了一些研究,胡云鹏等[12]在电流幅值最大为 1 500 A 时,求解空心电抗器周围磁场分布以及输出柜的涡流损耗,将涡流损耗作为主要的热源,根据电磁学和热力学理论建立电抗器的三维磁热耦合有限元模型;葛研军等[13]设计了一种外转子为永磁转子而内转子为铜套转子的磁耦,通过对涡流损耗进行理论分析与仿真计算,验证了永磁体极数及气隙长度对涡流损耗的影响;王雷等[14]提出一种基于流固耦合速度场计算散热系数进而分析耦合器温度场的方法,并进行三维温度场数值模拟,得到耦合器温度场分布;张河山等[15]将计算得到的绕组铜耗、定子铁芯损耗、永磁体涡流损耗以及杂散损耗等作为热源,采用磁热耦合法将其耦合到各部件进行瞬态温度场研究。
熵产分析的目的是使系统的做工损失降到最小,使系统所做的有用功最大化,降低熵产可提高系统的传动效率[16]。然而上述的诸多研究中仅单一考虑通过多场耦合能量分析双盘式磁力耦合器的散热问题,多数研究并未将其与熵产有效结合,仅是将一方面作为优化目标是不全面的[17],增加散热量的同时会造成系统熵产值的增大,因此这也是双盘式磁力耦合器参数优化的难点,如何在保证散热量的前提下尽可能降低系统的熵产值。为此本文针对矿用双盘式磁力耦合器的散热量和熵产,以热力学模型为基础,采用有限元法模拟传动过程,以获取散热量与熵产;采用人工蜂群算法(Artificial Bee Colony,ABC)优化的高斯过程回归方法(Gaussian Process Regression,GPR)构建有限元仿真的代理模型,并采用多目标粒子群优化算法(Multi Objective Particle Swarm Optimization,MOPSO)获取最优参数。
1 双盘式磁力耦合器的热力学模型
1.1 工作原理
双盘式磁力耦合器主要由输入轴、铜盘、永磁体盘、调隙装置、输出轴等组成。输入端通过轴套与驱动电机相连,轴套固定在导体轭铁上,导体轭铁既可以固定铜盘作用又可以引导永磁体产生的磁力线,使更多磁力线进入铜盘,提高传递效率,铜盘通过内六角螺栓固定在导体轭铁上,永磁体嵌镶在铝制的永磁体盘内,防止永磁体间漏磁,铝盘固定在永磁轭铁上。永磁体、铝盘和法兰盘组成永磁体盘,2个永磁体盘通过调隙装置连接,呈对称布置。铜盘和永磁体间的距离相等,永磁转子盘固定在输出轴上,如图1所示。
当铜盘随输入轴一起旋转时,铜盘与永磁体盘之间形成转差,根据法拉第电磁感应定律,磁通量通过铜盘以一定规律发生变化,交变磁场在铜盘上产生涡流,涡流产生的感应磁场与永磁体磁场之间共同作用下产生力矩,并在铜盘表面产生热量。产生的力矩驱动永磁体盘随着铜盘做同向旋转,带动输出轴转动,从而将动力传递至负载。

图1 双盘式磁力耦合器模型Fig.1 Double disk magnetic couple model
1.2 模型原理
如图2所示,建立的模型包括热源、铜盘、导体轭铁以及散热翅片。铜盘连接热量产生处,导体轭铁连接翅片,可使铜盘上产生的热量均匀的依次传递至导体轭铁、翅片,最终利用翅片表面与环境的热交换带走热,避免铜盘表面堆积大量热量。除此之外,各个连接处均采用导热胶填补,达到减少各元件之间接触热阻的目的[18]。由于双盘式磁力耦合器左右两侧具有对称性,为了简化计算量,故只分析左侧传热模型。
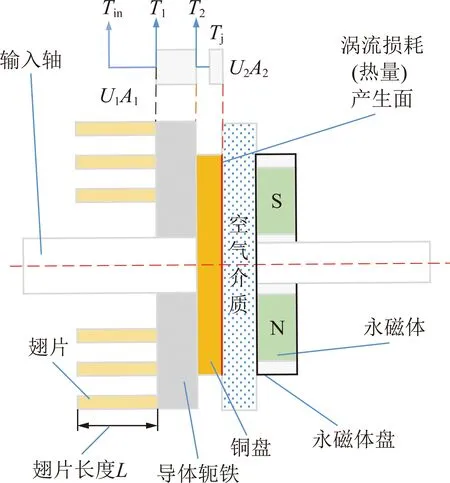
图2 双盘式磁力耦合器传热模型Fig.2 Heat transfer model of double disk magnetic coupler
图2中,Tin,T1,T2和Tj分别为背景温度、冷端温度、热端温度、涡流温度;U2A2和U1A1为热端、冷端的传热性能[19-20];U2为热端电压;A2为热端面积;U1为冷端电压;A1为冷端面积。
1.3 热力学分析
与导体轭铁的电阻相比,联接处的接触电阻很小,可忽略。故在建立热平衡方程时,忽略接触热阻,传热模型的热平衡方程如下:
q1=ST1r-0.5r2R-K(T2-T1)
(1)
q2=ST2r+0.5r2R-K(T2-T1)
(2)
其中,q1为散热量,W;q2为铜导体盘上产生的热量,W;S为传热模型的总塞贝克系数;r为输入电机的转速,r/min;R为传热模型的电阻;K为总热导,W/K;S,K,R均为重要的物性参数。对该模型进行传热过程推导,可得散热量与温差的计算公式为
(3)
(4)
式中,η为等效效率;i为铜导体盘上产生的电流。
散热量还可用式(5)表示:
q1=(Tj-T1)U1A1
(5)
联合式(1)~(5),推导出冷热两端的温度数学式。根据电磁感应原理,铜导体表面涡流温度Tj以及导体轭铁上翅片所处的背景温度Tin,可根据式(6)和(7)依次得出温度T1和T2,即
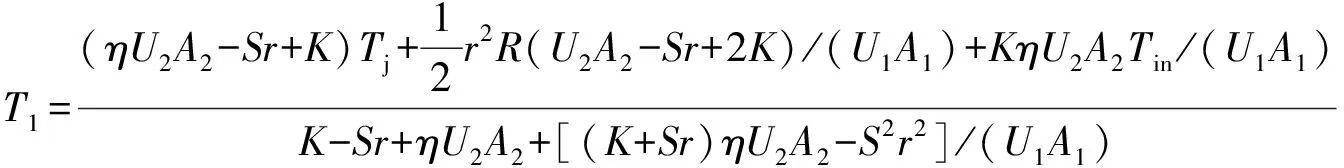
(6)
(7)
为分析该过程的熵产大小,则熵产Sg为
(8)
2 基于Ansoft-3D仿真的数据获取
Ansoft-3D获取目标变量对应的散热量与熵产的操作主要包括3步:前处理、模拟过程、后处理[21]。前处理主要考虑:三维模型、Maxwell模型、热传导模型、网格划分、傅里叶定律、设计参数的选择。前处理的参数经过Ansoft-3D仿真的求解器转换得到涡流温度。散热量和熵产可由涡流热量经过相应的公式转化得到,图3为仿真流程。
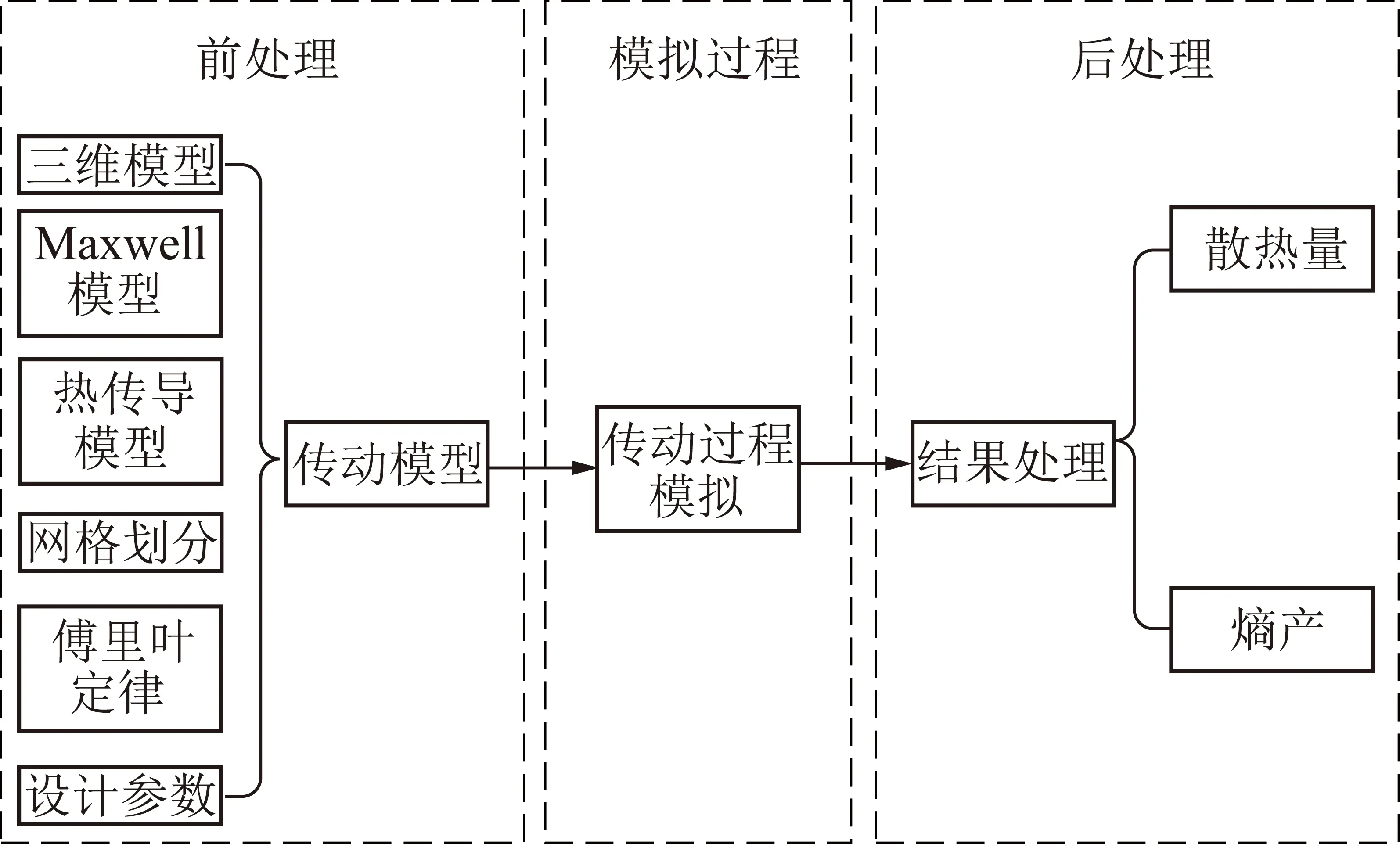
图3 仿真流程Fig.3 Simulation flow chart
2.1 Ansoft-3D前处理的关键技术
采用Solidworks软件完成双盘式磁力耦合器永磁体盘、铜导体盘的三维模型建立,以.x_t形式导入Ansoft-3D软件中,如图4所示。

图4 网格划分Fig.4 Grid division
参数项的设置会造成仿真结果与实际结果的误差,其中永磁体盘和铜导体盘网格数目根据仿真调试得出,其他模型与参数根据相应的文献参考选择[22]。将双盘式磁力耦合器传动过程中可控因素的输入电机的转速nin、翅片个数N,翅片长度L,永磁体盘与铜盘之间的气隙长度Lg作为仿真的输入,探索输入与散热量、熵产2个目标之间的关系,为此设计了四因素五水平的正交试验来进行仿真分析,各参数的取值见表1。
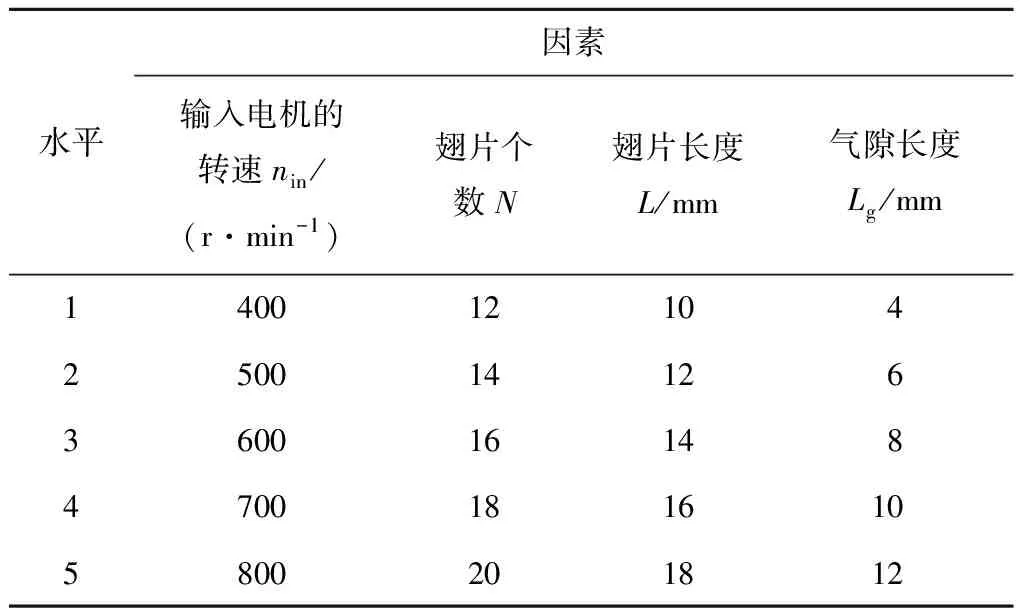
表1 正交试验切削参数
2.2 单参数分析
对单参数进行分析,以确定输入电机转速、气隙长度、翅片个数、翅片长度等参数对散热量和熵产的影响。参考煤矿井下工作温度,设置环境温度为22 ℃,图5(a)为输入电机转速与散热量的关系,图5(b)输入电机转速与熵产的关系。可以看出散热量随着输入电机转速先增加后减少,这是因为式(1)中其他参数为定值时,散热量q1关于输入电机转速r呈二次抛物线关系。由式(8)可知,Tin和Tj固定时,熵产只与q1,q2之差有关,故熵产随着输入电机转速单调增加。
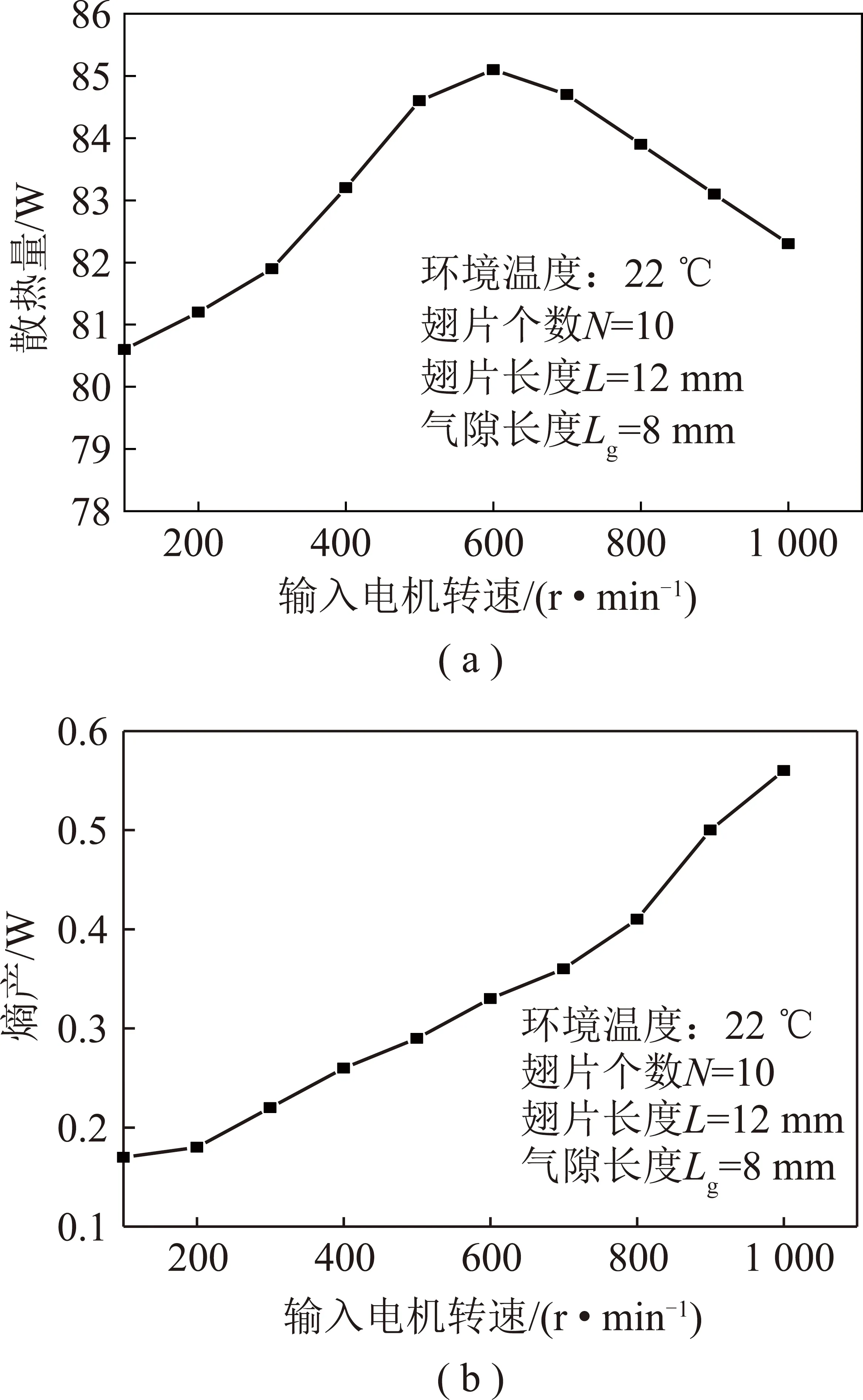
图5 散热量、熵产和输入电机转速关系Fig.5 Relations among heat dissipation,entropy generation and input motor speed
塞贝克系数S与翅片个数N呈线性关系[16],结合式(1),当其他参数固定时,散热量q1与S也呈线性关系,故如图6(a)所示,散热量随着翅片个数单调增加。图6(b)中,当Tin和Tj固定时,熵产依然只与q1,q2之差有关,故熵产随着输入电机转速单调增加。熵产仍随着翅片个数的增加而增大。
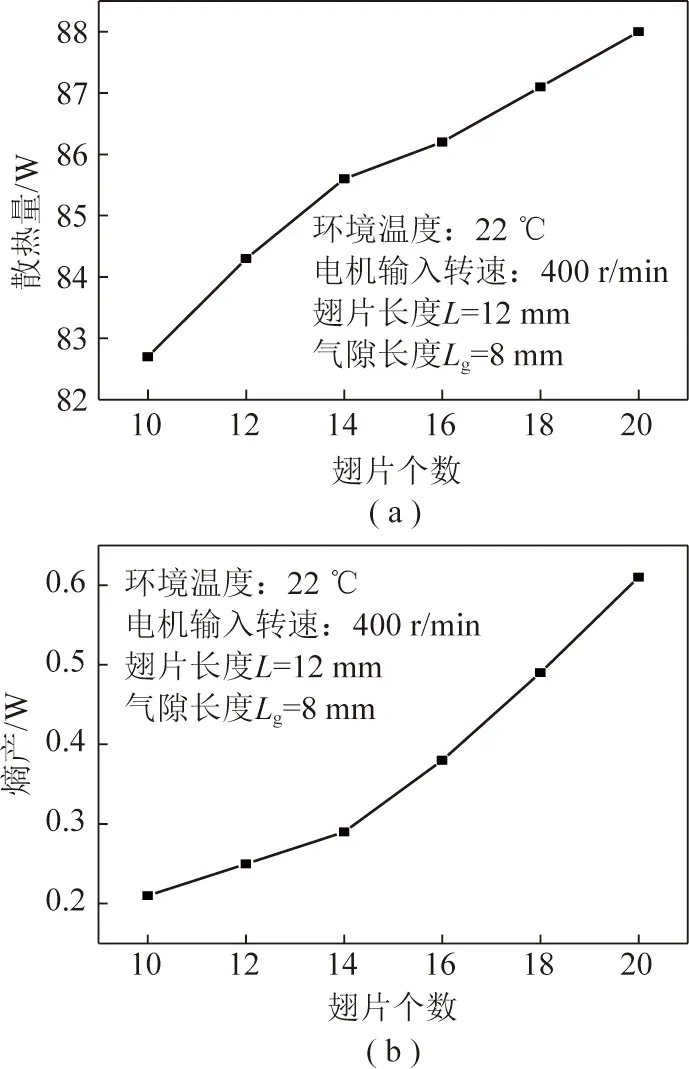
图6 散热量、熵产和翅片个数关系Fig.6 Relations among heat dissipation, entropy production and number of fins
如图7(a)所示,翅片长度直接影响热导K及电阻R大小,散热量q1随翅片长度增大而增大,但是当翅片长度达到14 mm后,散热量增加不明显。当环境温度较小时,熵产随着翅片长度变化不明显,因而整体较为平稳,如图7(b)所示。

图7 散热量、熵产和翅片长度关系Fig.7 Relations among heat dissipation,entropy production and length of fins

图8 散热量、熵产和气隙长度关系Fig.8 Relations among heat dissipation, entropy production and air gap length
当气隙长度增大时,造成气隙的等效磁阻增大[13]。散热量随着气隙长度增大而减小,这与式(1)符合。但是当气隙长度增加至8 mm后,散热量的变化量逐渐减小,趋近于水平线,如图8(a)所示。熵产随着气隙长度增大而增大,一旦增大至8 mm以后,熵产增加量不明显,如图8(b)所示。
选取环境温度为22 ℃,气隙长度为6 mm,输入电机转速为400 r/min,翅片长度依次为10,12,14,16 mm的涡流密度云图如图9所示。由图9可知,当翅片长度逐渐增加时,模型的最低温度在翅片外端,涡流密度最低值依次为3 300,2 752,928.64,648.82 W/m2。这与理论计算式(1),(2)相吻合:翅片越长,与空气接触的散热面积增加,使电阻R越小,则散热量增加,而传动过程中产生的涡流热量降低。
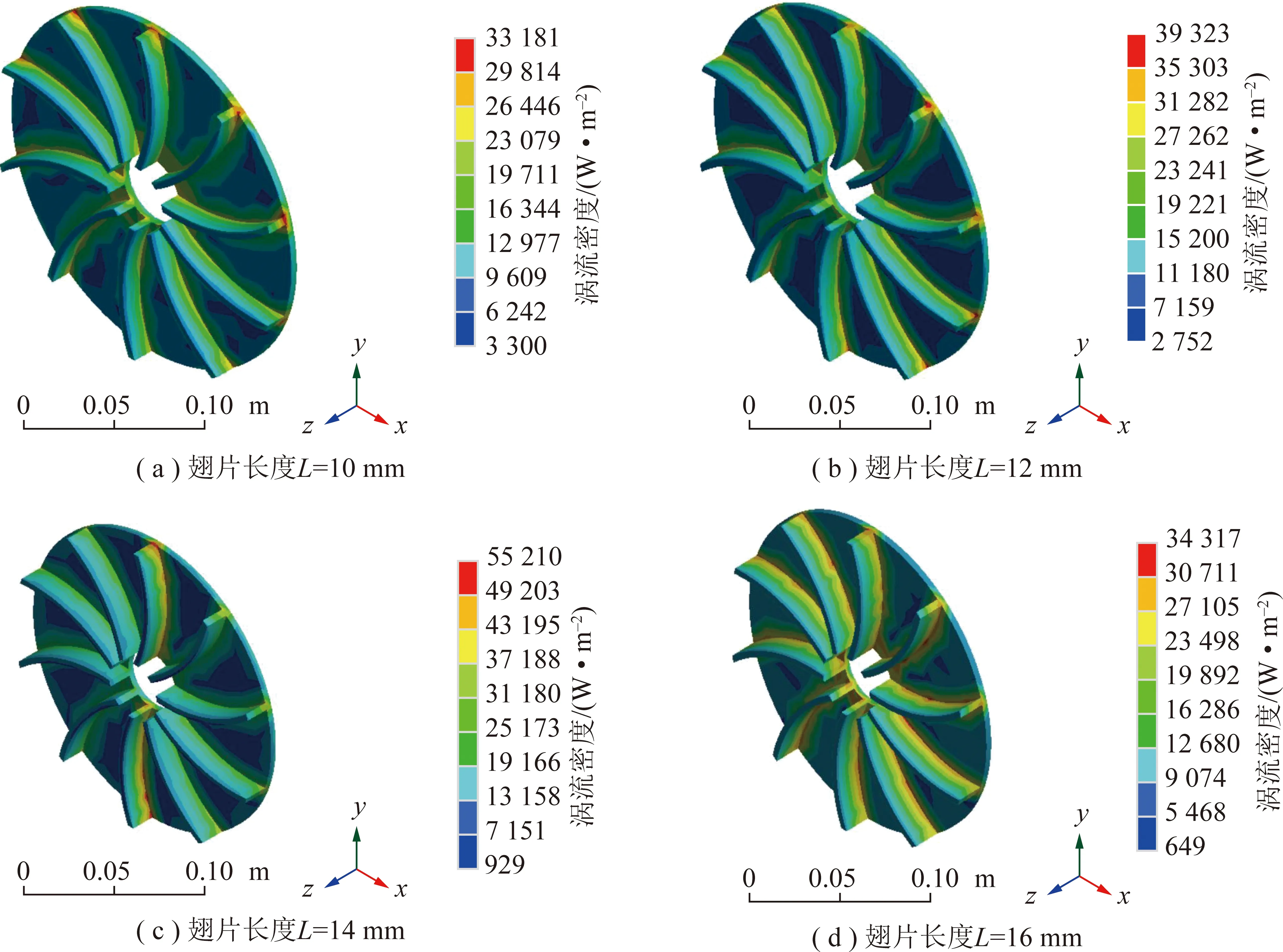
图9 仿真云图Fig.9 Simulation diagram
3 物理试验的验证
3.1 物理平台的搭建
为了验证上述理论分析与有限元仿真的结果,选取与仿真相同的参数在双盘式磁力耦合器上进行永磁涡流传动试验,现场试验平台如图10所示。

图10 试验平台Fig.10 Test platform
三相异步电机采用380 V三相低速电动机。通过变频器控制电动机,本实验台额定功率为55 kW,最大转速为3 000 r/min,建议转速为0~2 000 r/min。测量回路配置NCTES3000转矩转速测量仪(测试精度:0.2%,量程:500 N· m)、MIK-2740温度巡检仪连接计算机完成信号采集和测量任务。采用西门子S7-200系列PLC进行连锁控制。
3.2 物理试验与有限元对比
对25组仿真与物理试验的数据进行正交试验。有限元仿真后在铜导体表面上选取3个不同位置采集涡流温度,最终以这3处涡流温度的平均值作为最终的涡流温度。而物理实验的涡流温度通过温度传感器2测量得到,将仿真和物理实验的涡流温度代入式(5)即可算出散热量q,代入式(1),(2),(8)可算出熵产Sg。正交试验方案和结果见表2,其中,因素A为输入电机的转速nin,r/min;B为翅片个数N;C为翅片长度L,mm;D为气隙长度Lg,mm。
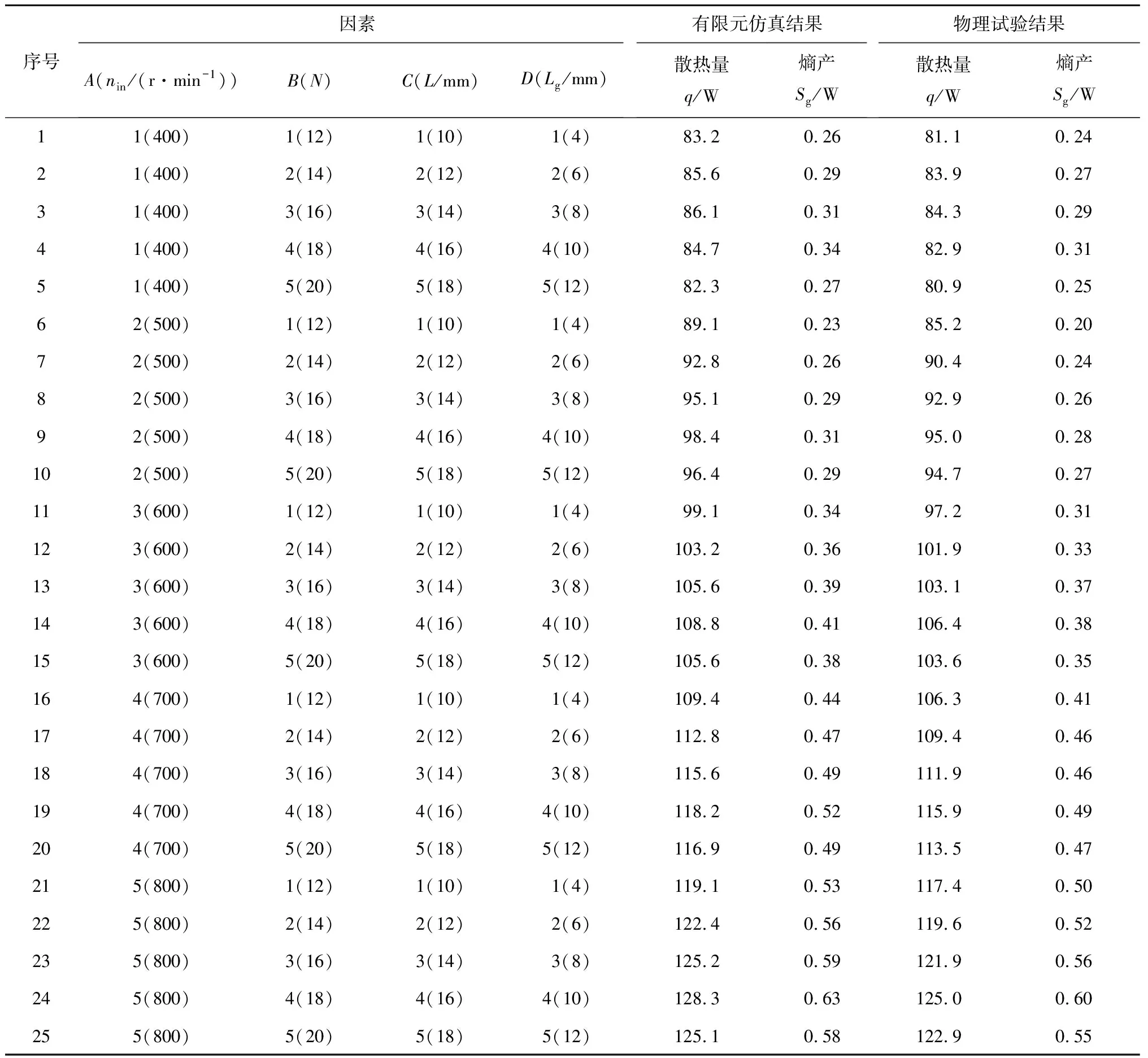
表2 正交试验设计方案以及仿真和物理试验结果
由图11可知,有限元仿真数据与物理实验数据具有相同的变化趋势,散热量与熵产误差的均值为4.6%和9.2%,基本验证了热力学模型和有限元分析的准确性。
4 考虑多物理场耦合与熵产分析的多目标优化算法的构建
高斯过程回归方法(GPR)在解决高维度输入、小样本空间与非线性问题上具有良好的性能,适宜作为处理第3节中正交试验数据的方法。采用人工蜂群算法改进的高斯过程回归模型作为有限元仿真的代理模型,该模型选择适用于非线性关系的平方指数协方差和线性协方差相结合的组合协方差函数[23]。基于Pareto分配关系,利用多目标粒子群优化算法,以散热量和熵产为目标优化参数,其流程图如图12所示。
需要优化的耦合能量和熵产之间存在着相互制约的关系。基于Pareto分配关系,改进人工蜂群算法构建高斯过程回归模型,采用多目标粒子群算法来解决两者之间的优化平衡问题。以永磁传动四要素为决策变量,以散热量和熵产作为优化目标,其优化问题可以表示为
(9)
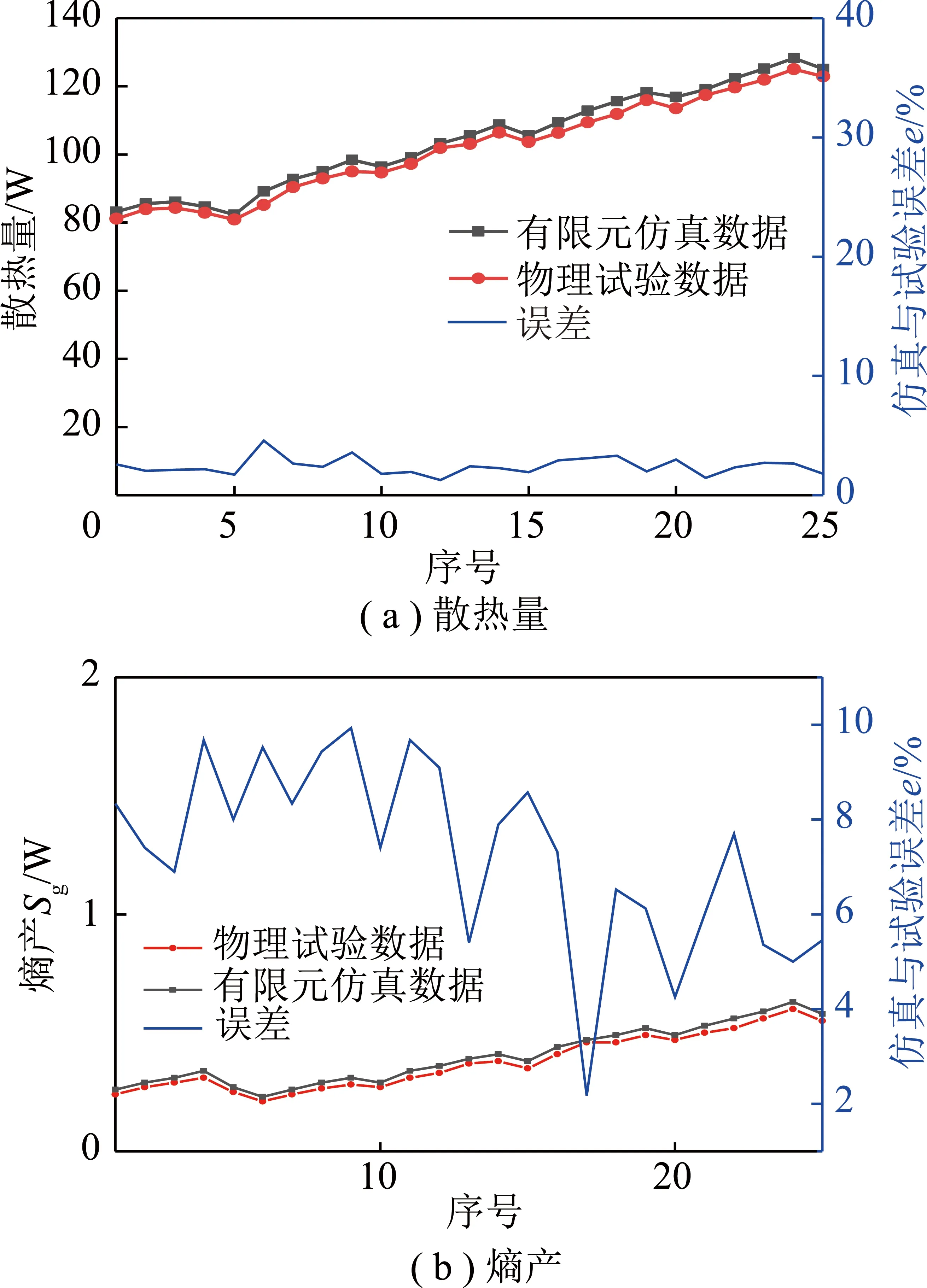
图11 物理试验数据与仿真数据的对比Fig.11 Comparison of physical test data and simulation data
该算法优化流程的具体步骤如下:
(1)初始化多目标粒子群的基本参数,见表3。在式(9)中给出的决策变量范围和最大最小粒子速度范围内初始化各粒子的速度xj和对应的速度vj,其中j∈[1,K]表示种群数;将改进人工蜂群算法构建的高斯 过程回归模型预测散热量和熵产的函数作为适应度函数,依据Pareto分配原则计算得到存放非劣解的archive集。

表3 优化基本参数设置
(2)根据粒子的适应度确定个体的最优解,然而当个体的最优解不能确定时,随机选取一个解作为个体历史最优,记为pbest;根据适应度范围和网格扩展因子确定网格范围并随之划分网格。计算archive集在网格中的拥挤度,并选择当前全体中拥挤度小的位置(种群最优解)记为gbest。
(3)更新archive集中粒子的速度、位置,以求解出粒子当前迭代过程中最好的pbest,表达式为
(10)
(11)
式中,k为当前迭代次数;C0为权重衰减因子;w为惯性权重,w(k+1)=C0w(k);c1,c2分别为个体与种群学习因子;r1,r2为0~1的随机数。
(4)通过比较当前迭代过程中全部粒子的适应度,将非支配解存储入archive集中,由此对archive集进行维护和更换。
(5)当算法迭代的次数达到预设的次数时程序就会停止,与此同时存储在外部档案中的所有解集就是Pareto前沿;若未达到条件要求则会返回步骤(1)。
5 结果对比与分析
5.1 改进人工蜂群算法-高斯过程回归模型的预测效果
将有限元仿真得到的25组数据作为改进人工蜂群算法-高斯过程回归模型的数据集,选取20组数据作为该模型的输入,其中15组为训练样本,5组为寻优样本,剩余5组为与预测值对比的样本。改进人工蜂群算法-高斯过程回归模型的散热量与熵产预测结果如表4和图13所示。仿真值与预测值吻合较好,且平均误差百分比(EMAP)依次为2.49%和7.80%,均小于10%,基本验证了该模型的有效性。
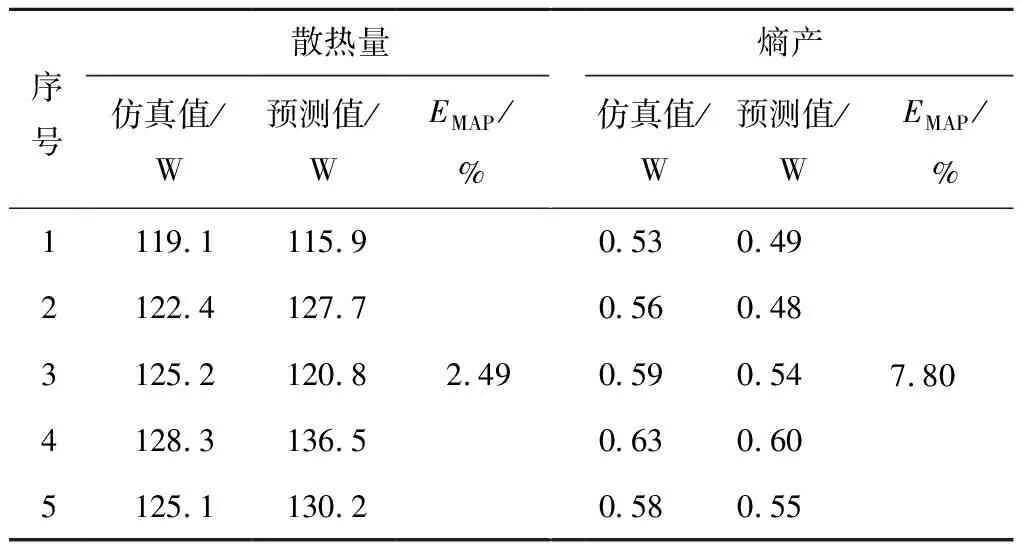
表4 预测值与仿真值对比
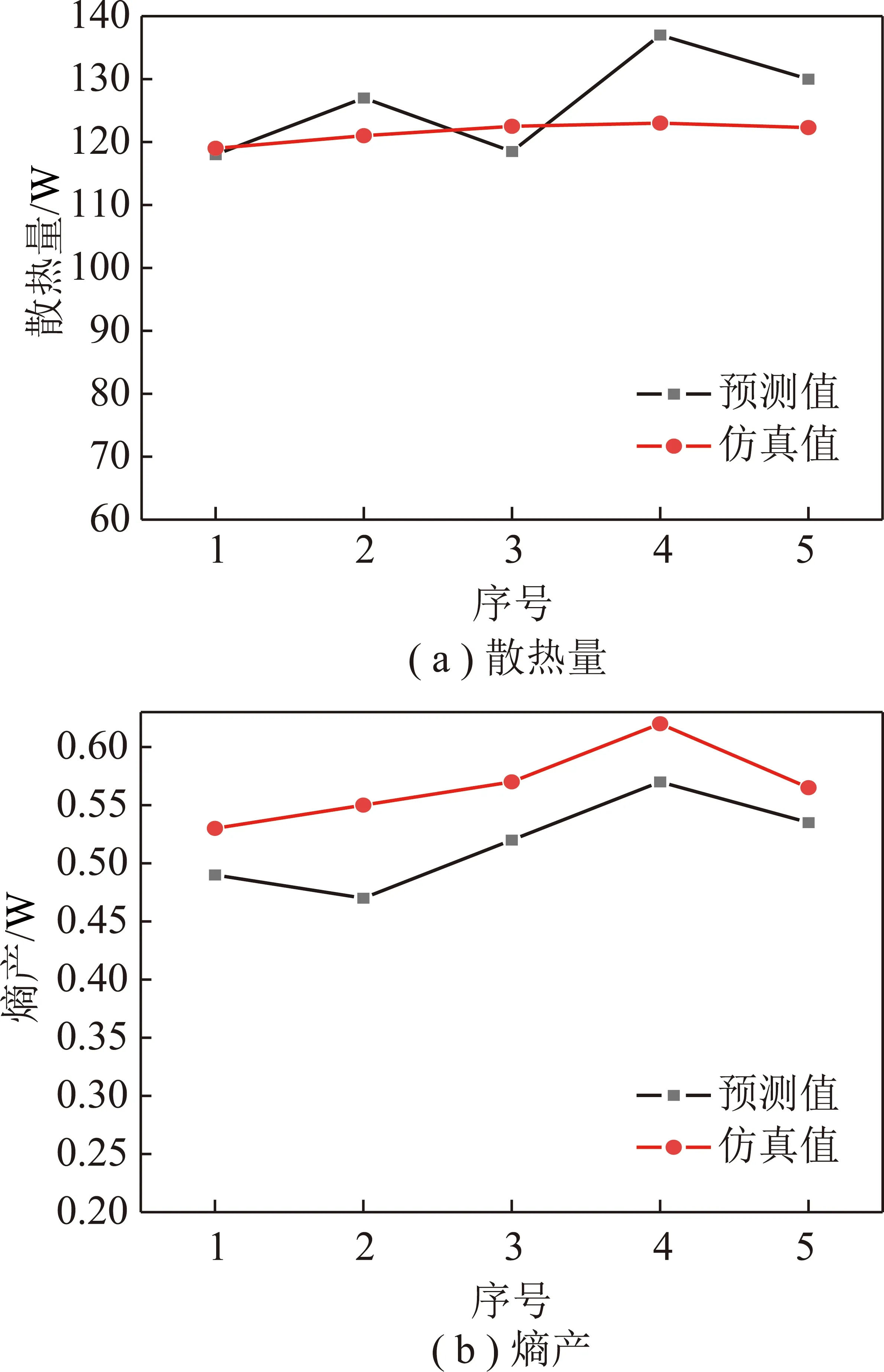
图13 预测值与仿真值对比Fig.13 Comparison between predicted value and simulation value
为对比改进人工蜂群算法-高斯过程回归模型的性能,本文采用天牛须搜索算法[24](Beetle Antennae Search algorithm,BAS)、粒子群优化(PSO)算法[25]分别优化高斯过程回归模型,构建天牛须搜索算法-高斯过程回归模型(BAS-GPR)和粒子群优化算法-高斯过程回归模型(PSO-GPR)。在以上3种模型下将预测散热量和熵产的效果进行了对比,并且采用模型精度的评价指标:均方误差(EMS)、EMAP、决定系数(R2)、对称平均百分比误差(ESMAP)和模型复杂度评判指标(运行时间T)来比较。其中,均方误差(EMS)、决定系数(R2)、对称平均百分比误差(ESMAP)的公式如下:
(12)
(13)
(14)
式中,ESS为残余均方根误差;TSS为方差总和。
3种优化算法依据EMAP、式(12)~(14)计算出各指标见表5。为了方便对比,将散热量和熵产预测效果较优的结果用下划线表示。综合看来,本文所提出的改进人工蜂群算法-高斯过程回归模型(ABC-GPR)的效果最优。而基于图13的预测趋势和均方误差(EMS)、EMAP、对称平均百分比误差(ESMAP)这些反映偏差的指标来说,预测趋势符合仿真模拟趋势。预测值和仿真值的平均偏差较小,2个表示百分比的指标(EMAP和ESMAP)均小于10%,因此可以认为利用改进人工蜂群算法-高斯过程回归模型(ABC-GPR)预测散热量和熵产具有可行性。
5.2 多目标优化结果及其验证
运行改进人工蜂群算法构建的高斯过程回归模型(ABC-GPR),采用多目标粒子群算法来解决散热量与熵产两者之间的优化平衡问题,算法运行结果如图14所示。其中黑色点不被其他点支配(Pareto前沿),蓝色点完全被其他点支配,红色点为个体最优解所对应的目标值。各设计参数下Pareto前沿以及目标值见表6。在其中选择一组优化后的参数{nin,N,L,Lg}={758 r/min,16,14.8 mm,6.6 mm},其对应的散热量和熵产依次为:128.2 W,0.41 W。将该组参数进行物理实验,以验证该优化算法的有效性。
基于以上搭建的双盘式磁力耦合器实验平台,按照优化后的设计参数设置,通过试验可得到对应的散热量和熵产。为了避免偶然性,对该组数据重复进行
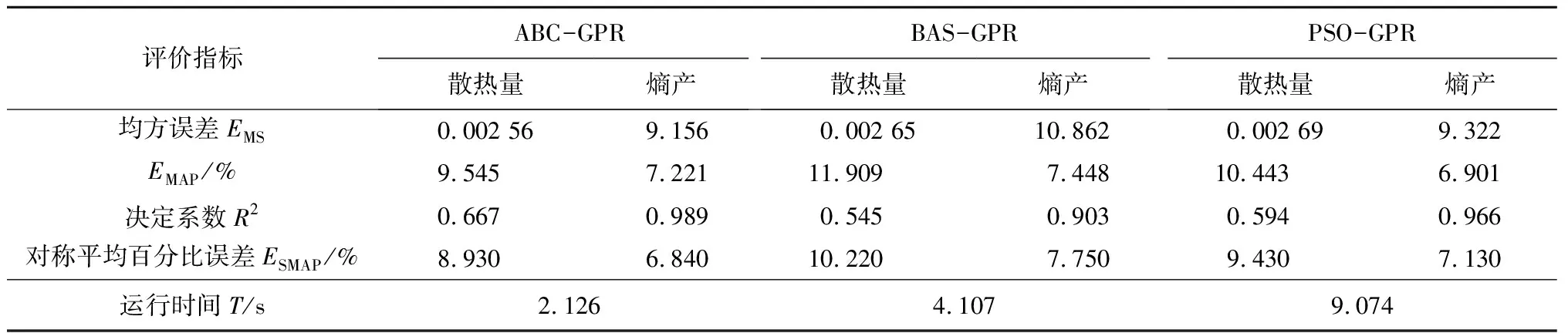
表5 3种优化算法各指标下的结果

图14 优化算法的Pareto解(黑色点方形点)Fig.14 Pareto solution of optimization algorithm (black dot and square dot)

表6 多目标优化结果
5次试验,得到的结果见表7。根据计算结果,散热量和熵产与相应优化结果的平均误差依次为5.614%,8.192%,该组优化后的参数满足实际传动期望达到的效果,可用于指导煤矿永磁涡流传动系统的设计。

表7 试验值
6 结 论
(1)基于能量平衡和熵产最小化理论,通过效率单元法和稳态热传递,建立了矿用双盘式磁力耦合器的热力学数学模型。利用有限元法仿真得到不同参数下的散热量与熵产,与对应的物理实验测量值具有相似的变化趋势,并且散热量与熵产的误差均值分别为4.6%和9.2%,基本验证了热力学模型和有限元分析的准确性。
(2)采用改进的人工蜂群算法(ABC)优化的高斯回归模型(GPR)对散热量和熵产的预测中,ABC算法预测的精度高于已有文献中的天牛须搜索算法(BAS)和粒子群算法(PSO)的预测精度,并且响应时间耗时也最少,仅为2.216 s。
(3)在ABC-GPR模型产生的参数与散热量和熵产之间的映射关系的基础上,利用多目标粒子群优化算法,得到了散热量和熵产的Pareto前沿。并采用物理试验验证了该结果的正确性,证明了该算法的可行性,有助于提高双盘式磁力耦合器的传动效率。
