一种估计接收机伪距硬件延迟的多频非组合PPP模型

张乾坤，柴洪洲，章 繁，田祥雨，王 敏

（信息工程大学 地理空间信息学院，郑州 450001）

近年来，用户端对快速精准定位服务的迫切需求使得新一代全球导航卫星系统（Global Navigation Satellite System,GNSS）精密定位技术迅速发展。为保障用户端定位的可靠性与稳定性，一般需要服务端事先估计各种偏差以供用户端改正，也因此推动了精密单点定位（Precise Point Positioning,PPP）模型中各种偏差项的深入研究。

组合PPP模型放大了观测值的量测噪声，且在处理多频观测数据时，需要依据某种条件在众多组合观测值中选取最优组合以进行周跳探测与修复处理[1]。而非组合PPP模型可避免观测量间组合引起的噪声放大问题，在处理多频数据时更为灵活[2]。此外，利用非组合PPP模型还可生成各类偏差产品如电离层延迟[3]、对流层延迟[4]、相位小数偏差[5]（Fractional Cycle Biases,FCB）等产品以供用户端改正，拓展了PPP的应用。值得注意的是，在传统的多频非组合PPP模型中，由于伪距和相位观测方程共用一组接收机钟差和卫星钟差，致使电离层延迟、相位模糊度参数吸收了卫星端与接收机端的伪距硬件延迟（Pseudorange Hardware Delay,PHD）。卫星端PHD虽无法直接获得，但可通过不同测距信号PHD间的差值，即差分码偏差（Differential Code Bias,DCB）以消除其对观测值的影响。这是因为卫星端DCB一般足够稳定，且对所有测站观测值的影响相同[6]，故可事先在服务端估计卫星端DCB以供用户端改正[7]。而接收机端的PHD一般认为会被接收机钟差、电离层延迟和模糊度参数完全吸收，也可通过星间单差的方法消除[8,9]，因此，在获取PPP浮点解时一般忽略了接收机端PHD的影响。然而，在获取PPP固定解时，若基于传统非组合PPP模型生成的各种产品，如电离层延迟和FCB产品，忽略了接收机端PHD的相关性质，则可能导致电离层延迟估值为负[10]、FCB估值不一致[11]等问题，进而影响用户端模糊度固定。

DCB改正在非组合PPP模型中是不能忽略的，但现有研究更关注卫星端DCB改正对观测值的影响，忽略了接收机端DCB的影响，而研究接收机端DCB的相关性质，尤其对GNSS电离层研究具有重要的意义。目前鲜有针对接收机端DCB较为系统的研究，文献[12]提出一种直接估计接收机端DCB的函数模型，并指出针对零基线，单天内接收机端DCB的变化趋势可用随机游走加以描述。文献[13]提出一种准实时估计站间单差接收机DCB的方法，其研究结果表明站间单差接收机DCB会受内置软件和观测条件变化而出现短期突变，全年日平均气温改变致使站间单差接收机DCB出现长期渐变性。文献[14]在联合采用iGMAS和MGEX测站网估计BDS-2、BDS-3的DCB时，发现BDS-2、BDS-3相应的接收机端DCB不一致，并将其归因于不同的接收机产商。文献[15]基于现有GIM和德国航空局提供的卫星端DCB产品，提出一种可估计短期内接收机端的DCB的方法。其结果表明大部分接收机的DCB单天内很稳定，且在连续时间内不会出现剧烈的跳变。此外，短期内接收机DCB存在明显的变化，若将接收机DCB视为常数处理，将会影响电离层TEC的提取。文献[10]提出一种估计接收机端DCB的GPS/BDS非组合PPP模型，与传统非组合PPP模型相比，估计接收机DCB参数的模型可提高模型的定位精度与收敛速度，且该模型得到的接收机端DCB估值在收敛后趋于稳定。以上研究针对不同方面对接收机端DCB展开了研究，但均未能详尽分析接收机端DCB的相关特性，尤其涉及到处理大量不同类型接收机构成的混合测站网的观测数据。此外，由于接收机端PHD一般难与其他参数直接分离，故现有研究也鲜有关注接收机端PHD的相关性质及其对定位的影响。

鉴于此，本文在详细推导传统多频非组合PPP模型中各待估参数间关系的基础上，提出一种可直接估计接收机端各频点PHD的多频非组合PPP模型。与传统多频非组合PPP模型相比，新模型中接收机钟差、电离层延迟和模糊度参数不再吸收接收机端的PHD，三者间的相关性可进一步降低。分别采用传统多频非组合PPP模型、估计接收机端DCB的多频非组合PPP模型与本文提出的新模型开展PPP定位实验，验证了新模型的有效性。此外，利用新模型生成的接收机端各频点的PHD估值，对不同类型接收机的PHD开展一系列分析与评估，得到一些有益的结论。

1 数学模型

本节首先以GNSS原始三频观测方程为例，介绍本文的PHD处理策略，然后导出估计接收机端PHD的多频非组合PPP模型。

1.1 观测方程

原始伪距和相位观测方程可表示为：

1.2 传统多频非组合PPP模型

1.3 估计接收机端PHD的多频非组合PPP模型

在1.2节的模型中，由于伪距和相位观测方程共用一个接收机钟差，致使接收机钟差、电离层延迟和模糊度参数分别吸收了部分接收机端的PHD，因此三者之间具有较强的相关性。

本文在1.2节模型的基础上，假设接收机钟差不再吸收接收机端PHD无电离层组合值dr,IF，而是将所有频点接收机端的PHD当作待估参数进行估计。此外，采用现有卫星端DCB产品来消除观测值中卫星端和的影响，可使接收机钟差、电离层延迟和模糊度参数不再吸收接收机端PHD，从而进一步削弱了PHD对电离层延迟和模糊度的影响，同时也可进一步降低参数间的相关性。估计接收机端PHD的多频非组合PPP模型如下：

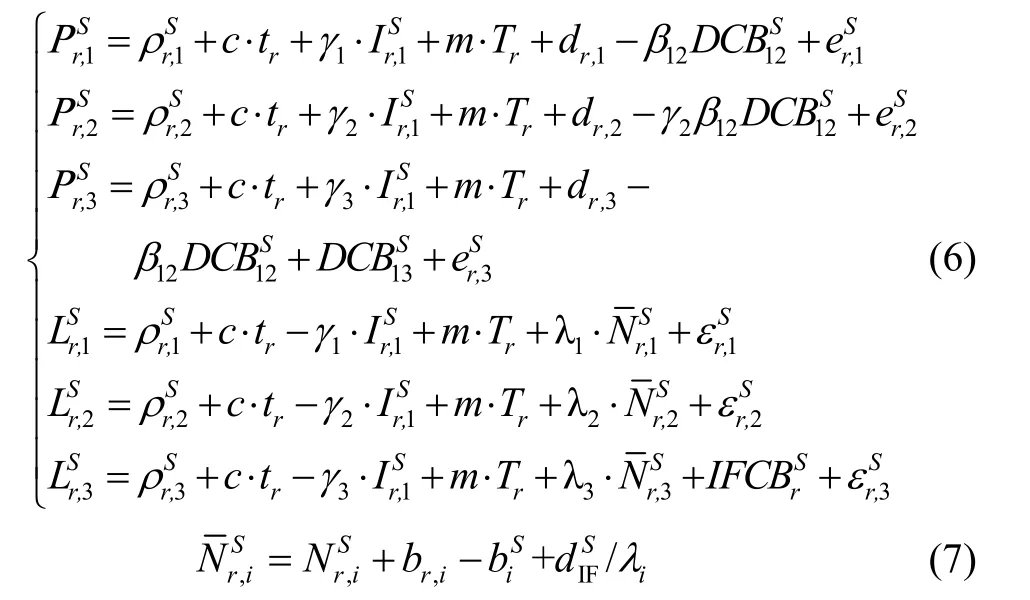
估计接收机端PHD的多频非组合PPP模型的待估参数如下：

从该模型的待估参数来看，该模型不但可获得较为“干净”的电离层延迟，还可获得接收机端伪距硬件延迟绝对量。若基于该模型同时处理现有多频观测数据，可实现单站估计接收机端多频PHD。实际上，在估计接收机端DCB参数的多频非组合模型中，模糊度参数仍吸收了接收机端的PHD，而新模型中模糊度参数不受接收机PHD的影响，这种差异在理论上会造成两种模型的模糊度参数收敛情况不同。由于模糊度参数收敛快慢及精度会影响PPP的定位性能，故新模型在理论上较估计接收机端DCB参数的多频非组合模型可取得更优的定位性能。

2 实验与分析

2.1 实验数据及处理策略

为验证新模型的有效性，从MGEX跟踪网中选取全球275个测站2021年DOY 001~007天的GPS多频观测数据，采样间隔为30 s。所选测站配备了不同厂商的接收机，包括Javad、Trimble、Septentrio和Leica，其具体的接收机信息如表1所示。

表1 接收机类型及测站数Tab.1 Receiver types and station number

所选测站全球分布见图1，其中蓝色、红色、绿色和黄色分别代表配备Javad、Trimble、Septentrio和Leica厂商接收机的测站。

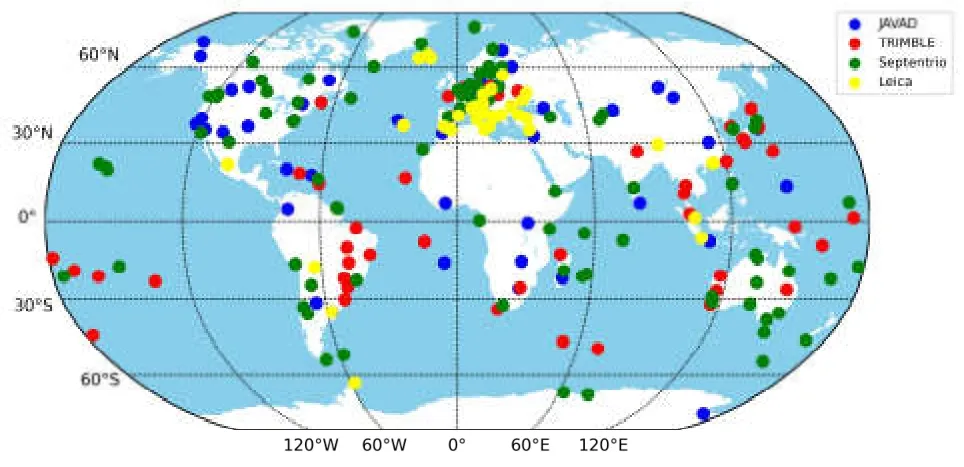
图1 测站分布图Fig.1 Distribution of selected stations

此外，本文同样实现了估计接收机端DCB的多频非组合PPP模型[10]。分别采用以下三种方案进行静态PPP定位实验。为减少数据运算量，在实际数据处理中将数据处理间隔设为1 min。

方案1：采用传统多频非组合PPP模型，以下简称UC-PPP；

方案2：采用估计接收机端DCB的多频非组合PPP模型，以下简称UC-PPP-rDCB；

方案3：采用估计接收机端PHD的多频非组合PPP模型，以下简称UC-PPP-rDrf；

三种方案中除PPP定位模型不同外，其他具体数据处理策略如表2所示。

表2 数据处理策略Tab.2 Processing strategies

2.2 三种定位模型性能评估

为评估三种多频非组合PPP模型的定位性能，分别依据上述方案进行PPP定位实验，并统计了每种实验方案在2021年DOY 001~007 7天的定位精度与收敛时间。在本文中，定位精度是指PPP定位结果与坐标参考值间的差值在平面和高程方向上的均方根误差（RMS）。本文采用IGS天解坐标作为定位结果的参考值，对部分没有提供天解坐标的测站，本文采用在线解算软件CSRS-PPP[20]与自编软件解算结果的平均值作为其坐标的参考值；收敛时间是指当水平或高程方向上的定位精度优于0.1 m且持续至少20个历元时，该时段第一个历元的时刻即为该方向上的收敛时间。

2.2.1 定位精度分析

图2-4分别为利用三种多频非组合PPP模型在平面和高程方向上定位精度平均值的散点图，其中不同颜色代表不同精度的定位结果。如图2-4所示，三种定位模型在平面和高程上散点的颜色分布基本一致，这表明利用三种定位模型在全球范围内得到的定位精度具有较好的一致性。

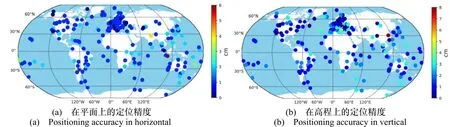
图2 UC-PPP模型在平面和高程方向上的定位精度Fig.2 Positioning accuracy of UC-PPP model in horizontal and vertical

图3 UC-PPP-rDCB模型在平面和高程方向上的定位精度Fig.3 Positioning accuracy of UC-PPP-rDCB model in horizontal and vertical

图4 UC-PPP-rDrf模型在平面和高程方向上的定位精度Fig.4 Positioning accuracy of UC-PPP-rDrf model in horizontal and vertica

表3统计了所有测站在E、N、U方向上DOY 001~007天内定位精度的最大值、最小值和平均值。如表3所示，在N和U方向上，三种模型间定位精度的差异在毫米级；在E方向上，利用UC-PPP-rDrf模型得到定位精度较其他两种模型可分别提高33.3%和14.3%。此外，在3D方向上，三种模型的定位精度分别为1.85 cm、1.73 cm和1.69 cm。由此可知，新模型在3D定位精度上较其他两种模型可分别提高8.55%和2.20%。以上结果表明，利用本文提出的新模型可在全球范围内取得的定位精度要优于其他两种模型。

表3 所有测站PPP定位误差的RMS值统计（单位：cm）Tab.3 Statistics of RMS value of PPP positioning error of all stations (Unit:cm)

2.2.2 收敛性分析

收敛性能是PPP定位模型有效性的另一个重要方面，为研究三种多频非组合PPP定位模型的收敛情况，本文进一步统计了所有测站在三种定位模型下的收敛时间分布。图5为采用三种模型得到的PPP定位解在E、N、U方向上收敛时间的箱线图及异常值占比图。图中Q1、Median、Q3和IQR分别为25%、50%、75%以及四分位数间距值（Inter-Quartile Range,IQR）。当PPP收敛时间小于Q1-1.5·IQR或大于Q3+1.5·IQR时，该收敛时间被视为收敛时间异常值，图中用“+”号表示。图中箱线图框的高度为四分位数间距，框内短线代表中位数。如图5所示，UC-PPP-rDCB和UC-PPP-rDrf两种模型的PPP定位解的收敛时间在E、N、U方向上的时间分布与异常值占比具有较明显的一致性，这表明两种定位模型的收敛性能基本一致。此外，三种模型的定位解在E方向上的收敛性能均为最差，其中利用UC-PPP模型得到的PPP定位解在E方向上有75%的收敛时间在73 min以下，而利用UC-PPP-rDCB和UC-PPP-rDrf两种模型的PPP定位解在E方向上有75%的收敛时间分别在56 min和58 min以下，且其异常值占比由传统模型的5.97%分别减小为3.74%和3.48%，这说明，UC-PPP-rDCB和UC-PPP-rDrf两种模型在E方向的收敛性能较UC-PPP模型有了明显的提高。三种模型的PPP定位解在N方向的收敛性能均为最优，其中位数分别为18 min、17 min和18 min，且其异常值占比最小，分别为4.47%、2.50%和2.85%；在U方向上的收敛性能次之，其异常值占比最大，分别为8.99%、6.55%、6.39%。从E、N、U方向上收敛时间的中位数来看，采用UC-PPP-rDCB和UC-PPP-rDrf两种定位模型的收敛性能具有较好的一致性，其间的差异在1 min内，且较UC-PPP模型可分别提高约21.2%、6.0%和4.0%。

图5 收敛时间分布箱线图及异常值占比图Fig.5 Box chart of convergence time and outlier proportion

为分析不同接收机类型对PPP收敛性能的影响，本文进一步统计了表1中配备不同类型接收机的所有测站在2021年DOY 001~007内的平均收敛时间。如表4所示，配备不同类型接收机的测站其PPP定位解的平均收敛时间明显不同。

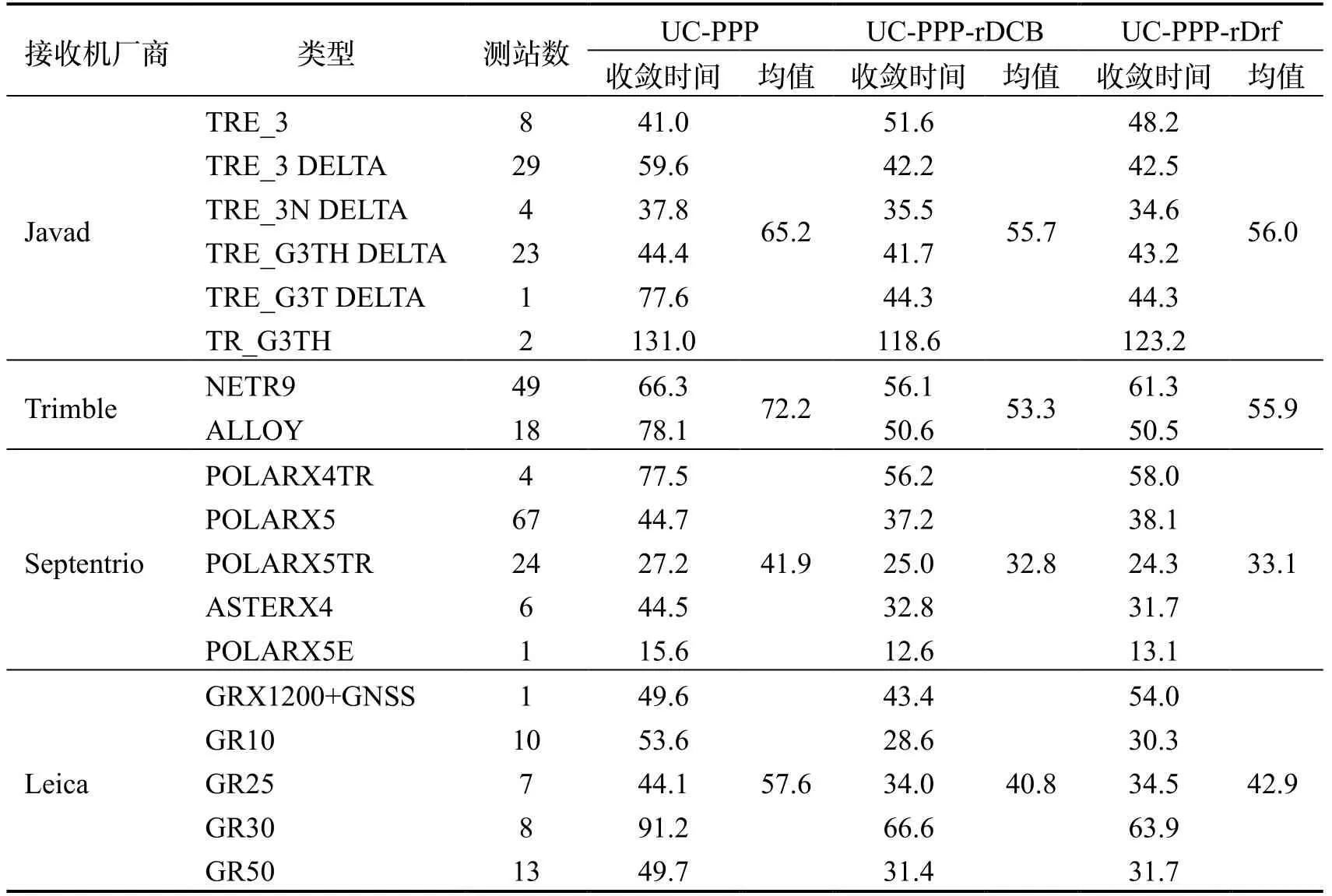
表4 不同类型接收机测站的平均收敛时间（单位：min）Tab.4 Average convergence time of the stations with different types of receivers (Unit:min)

总体来看，所选测站中配备了Septentrio厂商的接收机的测站数量最多，其平均收敛时间最短，配备Trimble厂商接收机的测站平均收敛时间最长，这表明不同类型接收机的收敛性能不同，这可能与不同类型接收机的观测质量有关。此外，利用三种定位模型得到的PPP定位解的平均收敛时间也有明显的差别，其中采用UC-PPP模型得到的定位解的平均收敛时间最长。相较于UC-PPP模型，采用UC-PPP-rDCB和UC-PPP-rDrf两种模型的PPP定位解的收敛性能有了明显的提高，这也说明本文所提出的UC-PPP-rDrf模型的有效性。

2.3 接收机端PHD的特性分析

与UC-PPP-rDCB模型的处理策略相同，在UC-PPP-rDrf模型中，将各频点PHD作为新的待估参数与其他待估参数一同进行PPP定位解算。两种模型在PPP解算后可分别获得单站接收机端的DCB（以下简称rDCB）、各频点PHD（以下简称rDrf）的估值。为研究基于两种模型获得的rDCB及rDrf估值与接收机类型的相关性及稳定性，本文进一步统计了所有测站在DOY 001~007内分别利用以上两种模型解算得到的rDCB与rDrf估值，其中rDCB12、rDCB13分别表示接收机端L1/L2、L1/L5频点间的DCB；rDr1、rDr2、rDr3分别代表三个频点上接收机端的PHD。

2.3.1 接收机端PHD的特性分析

限于篇幅，本文任意选取了MATZ、USN7两个测站分别在2021年DOY 004和DOY 007两天的rDCB与rDrf估值，以分析接收机端的PHD和DCB估值在单天的稳定性。如图6所示，两测站的rDrf和rDCB估值序列在收敛后呈平稳趋势，这说明两种模型中新加入的参数具备很好的收敛性。此外，从图中同样可看出，两测站的rDrf和rDCB估值序列的均值不同，其原因与两测站配备了不同的接收机类型有关。为进一步分析由两种模型解算得到的接收机端PHD和DCB估值与接收机类型间的相关性，本文分别统计了所有测站2021年DOY 001~007内rDr1、rDr2、rDr3与rDCB12、rDCB13估值的均值。为便于统计分析，所有测站接收机端的PHD和DCB均值按表1中的接收机类型进行分类。

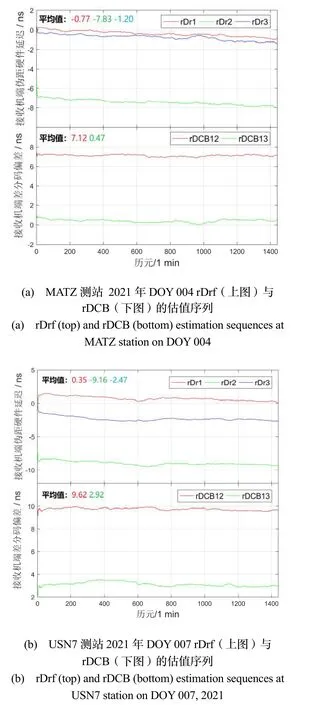
图6 两测站rDrf和rDCB单天解的序列图Fig.6 Single-day solutions of rDrf and rDCB at two stations，2021

图7为所有测站采用UC-PPP-rDrf模型得到的rDr1、rDr2、rDr3的均值分布情况，图8为所有测站采用UC-PPP-rDCB模型得到的rDCB12、rDCB13的均值分布情况，其中不同颜色的实心点代表不同类型的接收机。如图7-8所示，不同类型接收机的rDr1、rDr2、rDr3与rDCB12、rDCB13均值有明显的差异，其中配备Trimble厂商接收机的rDrf与rDCB均值在图7-8中呈明显的“离群”现象。此外，相同厂家不同类型接收机间的rDrf和rDCB的估值也不同，如Leica GR10、Leica GR25两种类型与Leica GR30、Leica GR50两种类型的rDrf和rDCB的均值在图7-8中的分布同样存在明显的差异。以上结果表明，接收机端的PHD和DCB与接收机类型具有明显的相关性。

图7 所有测站2021年DOY 001~007 rDrf均值的分布情况Fig.7 rDrf mean values of all stations on DOY 001~007,2021

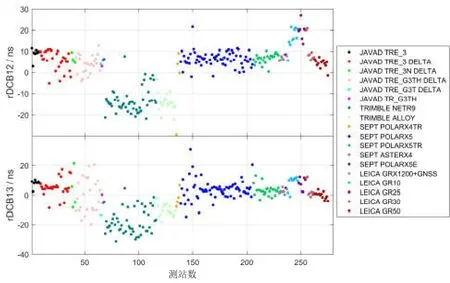
图8 所有测站2021年DOY 001~007 rDCB均值的分布情况Fig.8 rDCB mean values of all stations on DOY 001~007,2021

从2.1节和2.2节的模型介绍可知，在UC-PPP模型中，模糊度吸收了rDCB12参数；在UC-PPP-rDCB模型中，模糊度吸收了rDr1参数。为进一步分析不同类型接收机各频点PHD与DCB的差异，分别统计了每种类型接收机的rDrf和rDCB 7天内估值的均值。如表5所示，对rDr1而言，除TRE_G3T DELTA、TRIMBLE NETR9和TRIMBLE ALLOY三种类型的rDr1值差异较大外，其他所有类型接收机的rDr1基本一致，其间的差异在2.0 ns内；不同类型接收机的rDr2和rDr3间的差异较大，其一致性要弱于rDr1。如表5所示，TRIMBLE厂商接收机的rDrf和rDCB均值与其他类型接收机的rDrf和rDCB均值具有显著的差异。而Septentrio厂商的接收机中，除POLARX4TR类型接收机外，其他类型接收机间的rDrf和rDCB均值表现出较好的一致性，其间的差异在2.0 ns内。此外，从表中同样可看出，不同类型接收机端的rDCB13均值分布差异较大，整体上的一致性要弱于rDCB12的均值分布。而Septentrio厂商的接收机中，除POLARX4TR类型接收机外，其他类型接收机间的rDrf和rDCB，表现出较好的一致性，其间的差异小于2.0 ns。以上结果表明，不同类型接收机端rDrf和rDCB均值具有明显的差异，其中rDr2、rDr3以及rDCB13的差异更明显，在处理包含接收机端PHD的参数估计时，需要考虑与接收机类型有关的PHD的影响。

表5 不同类型接收机各频点PHD与DCB的均值统计表（单位：ns）Tab.5 Mean values of PHD and DCB at each frequency of different types of receivers (Unit:ns)

2.3.2 接收机端DCB的一致性分析

从1.2~1.3节的模型介绍可知，利用UC-PPP-rDCB模型解算后可直接得到rDCB12和rDCB13的估值。利用UC-PPP-rDrf模型解算后虽只能得到rDr1、rDr2、rDr3估值，但可分别通过rDr1与rDr2、rDr1与rDr3间作差得到相应的rDCB12、rDCB13值。为了分析由两种模型得到的rDCB12、rDCB13间的一致性，通过两者互差得到rDCB12、rDCB13间的互差值ΔrDCB12、ΔrDCB13。如图9所示，所有测站的ΔrDCB12、ΔrDCB13都在0.40 ns以内，且对于ΔrDCB12，有71.64%的测站其互差值在0.10 ns以内，91.64%的测站其互差值在0.20 ns以内；对于ΔrDCB13，有75.64%的测站其互差值在0.10 ns以内，94.18%的测站其互差值在0.20 ns以内。以上结果表明，利用两种模型得到的rDCB12与rDCB13间的互差值较小，说明由两种模型得到的接收机端DCB具有较好的一致性，同时也能反映出两种模型的等价性。

2.3.3 接收机端DCB的可靠性分析

为进一步分析利用UC-PPP-rDCB和UC-PPP-rDrf两种模型得到的接收机端差分码偏差rDCB的可靠性，以CAS提供的接收机端DCB产品作为参考值，分别统计了由两种模型得到的接收机端DCB与参考值间互差的结果。值得注意的是，CAS的产品只包含了部分测站接收机端DCB产品，因此本文在统计中，只对比了相同测站的DCB互差结果。如图10所示，由两种模型得到的rDCB12与CAS的rDCB12产品具有较好的一致性，分别有56.14%和54.39%的测站其互差值小于1.0 ns，且均有92.98%的测站其互差值小于3.0 ns。而利用两种模型得到的rDCB13与CAS的rDCB13产品的一致性要稍弱于rDCB12，均有40.38%的测站其互差值小于1.0 ns，分别有84.62%和82.69%的测站其互差值小于3.0 ns。这是因为估计rDCB所采用的策略不同，且CAS未提供接收机端C1W-C5Q和C1W-C5X的差分码偏差产品，因此，本文假设其接收机端DCB产品足够稳定，通过对CAS产品中C1C-C1W、C1C-C5Q、C1C-C5X间互差得到相应的rDCB13产品作为参考值，而UC-PPP-rDrf和UC-PPP-rDCB两种模型可直接获得C1W-C5Q、C1W-C5X的差分码偏差。以上结果表明，利用两种模型得到的rDCB估值与CAS提供的rDCB产品虽有一定的偏差，但整体上具有较好的一致性，这同时也验证了本文提出的新模型的可靠性。

图10 两种模型得到的rDCB与CAS提供的rDCB产品间的互差情况Fig.10 The difference between the rDCB obtained by the two models and the rDCB products provided by CAS

3 结论

本文提出一种可直接估计接收机端PHD的多频非组合PPP模型，实现了电离层延迟、模糊度参数与接收机端PHD的有效分离，有效提升了模型的定位性能。通过实验验证，得出以下几点结论：

（1）本文提出的新模型在定位精度上优于UC-PPP模型和UC-PPP-rDCB模型，其中在E方向较其他两种模型可分别提高33.3%和14.3%，在3D方向上较其他两种模型可分别提高8.55%和2.20%。此外，新模型的收敛性能与UC-PPP-rDCB模型相当，均优于UC-PPP模型，在E、N、U方向上的收敛速度较UC-PPP模型可分别提高约21.2%、6.0%和4.0%。

（3）不同类型接收机的收敛性能不同，其中配备Septentrio厂商接收机的测站平均收敛速度最快，而配备Trimble厂商接收机的测站平均收敛速度最慢。

（2）由UC-PPP-rDrf得到的接收机端各频点的rDrf估值和由UC-PPP-rDCB模型得到的接收机端rDCB估值均与接收机类型相关。Trimble厂商接收机的rDrf和rDCB估值与其他类型接收机的rDrf和rDCB估值间具有明显的差距，而Septentrio厂商的接收机，除POLARX4TR类型外，其他类型接收机间的rDrf和rDCB估值表现出较好的一致性，其间的差异小于2.0 ns。此外，由接收机端各频点PHD估值转换得到的rDCB与UC-PPP-rDCB模型的rDCB估值一致性较好，二者之差优于0.40 ns。

本文的研究结论还有待采用其他GNSS系统接收机类型更多、观测时段更长的观测数据加以进一步验证与完善。此外，本文提出的模型实现了模糊度参数与接收机端PHD的有效分离，理论上可避免在利用混合接收机类型的测站网估计FCB时，其产品受与接收机类型有关的PHD的影响。因此，探究本文所提出的多频非组合PPP模型对采用混合接收机类型测站网估计多频FCB及模糊度固定的优势，也是下一步将要开展的研究工作。