利用探空产品评估GNSS-PPP估计ZTD精度

赵 涛，夏朋飞，叶世榕

(1.武汉大学GNSS技术研究中心，武汉 430072；2. 武汉大学测绘学院，武汉 430079)

0 引言

全球导航卫星系统(Global Navigation Satellite System，GNSS) 具有全天候、连续性、全球覆盖等优势。在满足全球导航和定位需求的同时，GNSS还可以向用户提供时间、速度和大气延迟等信息，因而在测量、军事、大气研究等领域得到了广泛的应用[1-3]。当前，利用GNSS技术探测对流层大气已成为国内外研究的热点，国内外研究者根据GNSS获得的天顶对流层延迟(Zenith Troposphere Delay，ZTD)反演对流层水汽时空分布信息，并将其成功地应用到了气象和气候方面的研究中[3]。在20世纪80年代，美国的Davis和Herring等在该领域利用GNSS数据进行了许多理论研究及实验，取得了丰硕的成果。随着GNSS观测精度的不断提高，GNSS信号的大气延迟效应已可用于地球大气的探测中[3]。一方面，GNSS定位中求得的天顶延迟改正项可以用来计算测站上空可降水汽量的垂直积分，这就是地基GNSS气象学；另一方面，一个安装在低轨卫星上的GNSS接收机在观测一个正在掩星过程中的GNSS卫星信号时，可用反演方法提供地球大气的压力、温度和湿度的详细剖面，这就是空基GNSS气象学[3]。

地基GNSS大气反演通常建立在局域地基GNSS网的基础上，通过双差处理消除卫星钟差的影响，可实时提供各测站上空的大气可降水量(Perceptible Water Vapor, PWV)[3]。由于距离较近的相邻测站ZTD具有相关性，双差模式只能获得测站间的相对PWV，而获取测站上空的绝对PWV则需要在网中某个测站上配置水汽辐射计进行定标才能实现。而GNSS非差模式，即精密单点定位技术可以直接获取测站上方的ZTD和绝对PWV。因此，GNSS精密单点定位技术估算ZTD一直是国内外研究的热点[4-5]。Shi研究了中国大陆对流层变化的特征[6],认为ZTD的结果与国际GNSS服务(International GNSS Service，IGS )一样具有很高的准确性和可靠性。国内外许多学者都对对流层延迟模型的精度进行了评估[7-9],其中一些学者分析了对流层延迟计算结果在不同地区的精度[10-13]，提出了新的对流层延迟反演方法[14-15]。

ZTD根据是否含有水汽可以分为2个部分：天顶对流层干延迟(Zenith Hydrostatic Delay, ZHD)和天顶对流层湿延迟(Zenith Wet Delay, ZWD)。ZHD变化较为平稳，利用经验模型可以高精度地获取ZHD。从ZTD中剔除ZHD后便可得到ZWD，利用湿度转换因子便可将ZWD转换为PWV。根据上述内容可知，ZTD的精度直接影响PWV的质量。因此，评估GNSS精密单点定位技术获取ZTD的精度是GNSS气象学研究和应用的必然趋势。Olaleken等分析了尼日利亚上空ZTD的时空变化[16]，ZTD估计显示各站之间的空间依赖性较弱。陈于等分析了IGS精密星历和钟差对ZTD精度的影响[17-18]，结果表明利用IGS精密轨道解算的ZTD与IGS提供的ZTD相当。Suparta等利用自适应神经模糊推理系统建立了南极天顶路径延迟模型[19]。Kalita等认为对流层延迟是影响精确点定位方法收敛时间的关键因素之一，讨论了对流层初始参数的方差和偏差对定位的影响[20]。

无线探空提供了高精度和高垂直分辨率的大气参数(大气压强、大气温度、相对湿度等)，利用这些大气参数可以计算出ZTD。本文试图将探空产品获得的ZTD作为真值来评估GNSS估算的ZTD。选取中国地区4个IGS测站的观测数据及其附近的探空产品进行试算，并解决了两类观测产品空间分辨率不一致性的问题。

1 探空产品估算ZTD

无线电探空仪简称探空仪，是随着探空气球上升，用敏感元件直接测量大气压力、温度和相对湿度层结曲线的无线电遥测仪，是高空气象站主要仪器之一。无线电探空仪由感应元件、转换电路、编码装置、无线电发射机和电源组成。大气高度上的温度、压力和湿度分别由温度、压力和湿度元件感应，其机械的或电的输出由转换开关依次接入编码器转变成电信号，再由发射机经调幅或调频发送，接收头在地面进行接收、解调和记录。利用探空测站历史探空数据计算ZTD，ZTD包括两部分分别为ZHD和ZWD，可以表示为

(1)

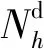
(2)

(3)

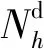
(4)

(5)

把式(4)和式(5)代入式(1),便可获得ZTD。

中性大气延迟一般泛指电磁波信号在通过高度为50km以下的未被电离的中性大气层时所产生的信号延迟。由于探空测站观测值的高度一般只到达对流层顶处，在对流层顶以上没有观测数据或者只有部分高程有数据，故需要考虑对流层顶以上高度大气层产生的延迟值。由于对流层顶以上的大气层上水汽值可以忽略不计，本文直接利用Saastamoinen干延迟模型估算探空产品对流层顶以上的ZTD来弥补探空观测值的不足。

2 匹配探空测站与GNSS测站空间分辨率

为利用探空产品获得的ZTD评估GNSS精密单点定位技术估算ZTD的精度，选取中国区域4个IGS观测站及其附近探空测站2014—2018年共5年的数据。选取的测站分布如图1所示。

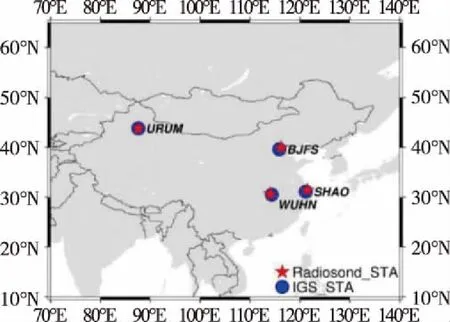
图1 GNSS测站及附近探空站的分布Fig.1 Distribution of GNSS stations and nearby radiosonde stations

本文利用Bernese 5.2软件，采用IGS分析中心提供的精密轨道和精密钟差文件，选用无电离层组合模型，将卫星截止高度角设置为7°，对GNSS观测数据进行处理，每1h输出一次接收机坐标及接收机上方的ZTD。由图1可以看出，GNSS测站与探空测站相距很近，一般在10km以内，为了进行对比分析，需要事先统一两种产品的时空分辨率。探空产品的时间分辨率为12h，而GNSS估算的ZTD为1h。故每天可抽取出GNSS测站与探空产品测站相同时间点的ZTD值进行比较来匹配二者的时间分辨率。此外，文中计算了匹配时间分辨率后的探空测站与GNSS测站之间的高程差，以BJFS测站和URUM测站与其对应的探空测站为例，绘制图形如图2所示。

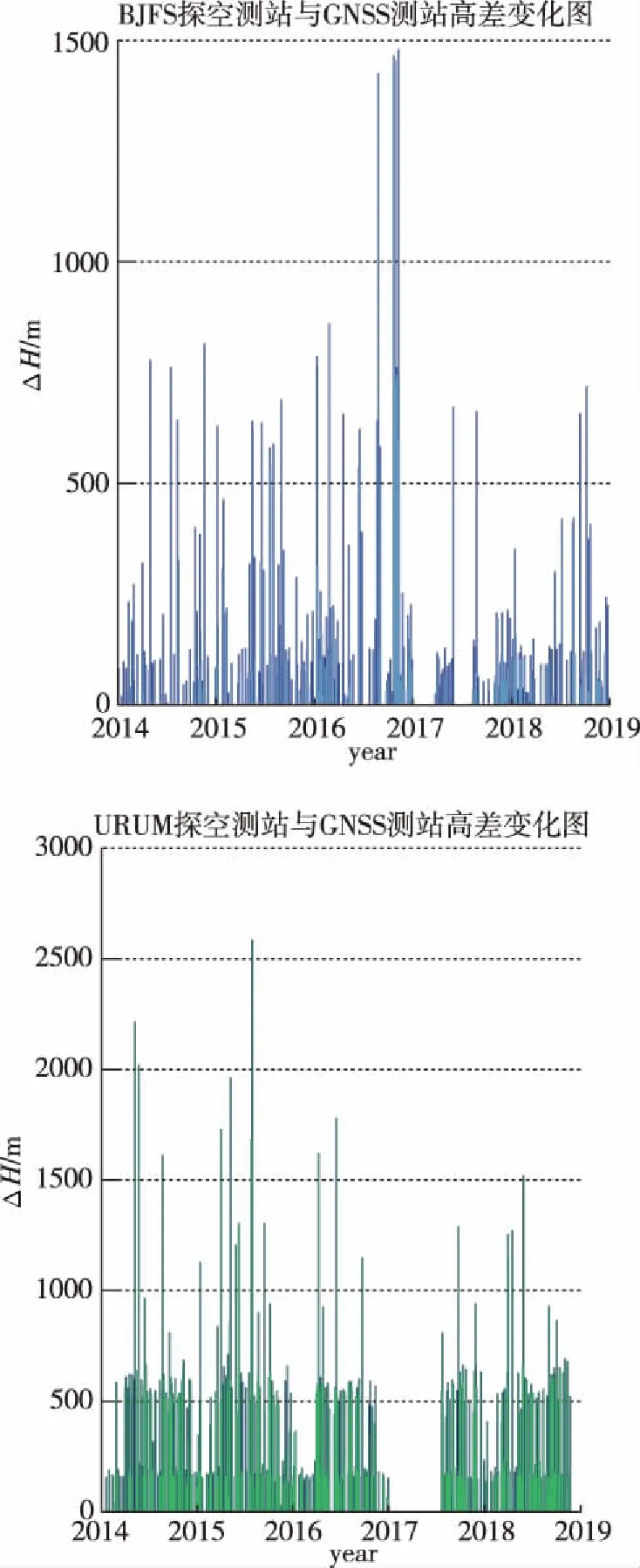
图2 探空测站与GNSS测站高程差Fig.2 Elevation difference between radiosonde station and GNSS station

由图2可知，时间分辨率匹配完成后，探空测站与GNSS测站部分时刻存在高程差。以BJFS测站为例，高程差的均方差为99.48m,平均偏差为19.62m, 最大偏差为1478m, 其他测站的统计数据在表1中给出。在这样的情况下，无法评估GNSS精密单点定位技术估算ZTD的精度。因此，利用GNSS测站配置的气象观测值作为探空测站的起始观测值，弥补探空测站起始高度与GNSS测站不一致时的天顶方向对流层延迟ZTD，达到匹配两者的空间分辨率的目的。

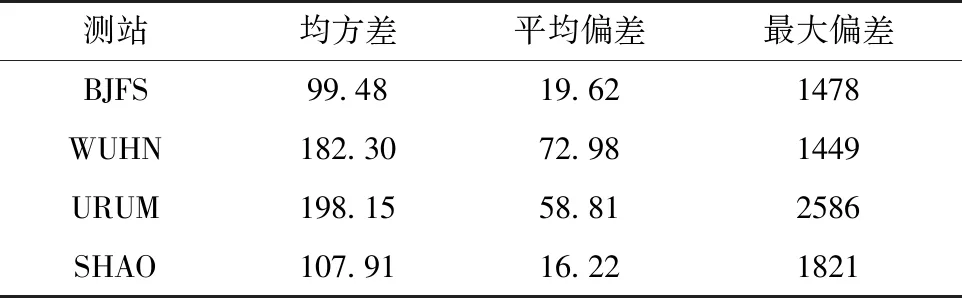
表1 探空测站与GNSS测站高程差统计表Tab.1 Statistical table of elevation difference between radiosonde stations and GNSS stations m

完成GNSS实测数据与探空测站数据的时空分辨率匹配后，绘制探空测站天顶方向对流层延迟随时间的变化图如图3所示,分别对应BJFS、WUHN、URUM和SHAO测站。

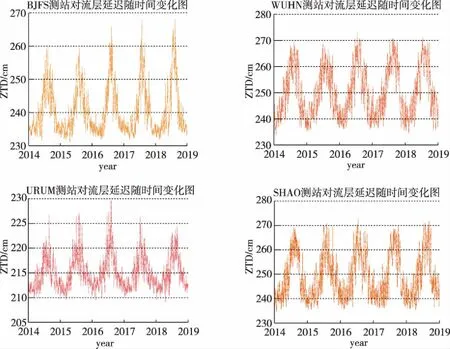
图3 探空测站对流层延迟随时间变化图Fig.3 Tropospheric delay with time in radiosonde stations

由图3可知，探空测站对流层延迟变化趋势可用三角函数进行较好的拟合，ZTD在一年中的变化具有明显的季节性，在气温高的季节较气温低的季节有明显的提升。这导致了许多对流层误差模型精度不稳定，难以做到精确化。因此，研究实测GNSS数据提供的对流层延迟的精度非常必要。

3 评估GNSS精密单点定位ZTD的精度

本文共选取中国地区4个探空测站的数据来评估利用GNSS精密单点定位技术估算ZTD的精度，并采用偏差(Bias)、均方差(Rms)、平均值(Mean)、最大值(Max)和最小值(Min)五种指标来评价其精度。

为了分析实测ZTD的偏差，本文分别求出了4个测站GNSS估算的ZTD与探空测站估算的ZTD之差。限于篇幅，文中仅给出了BJFS测站和URUM测站的ZTD偏差序列DZTD，如图4所示。

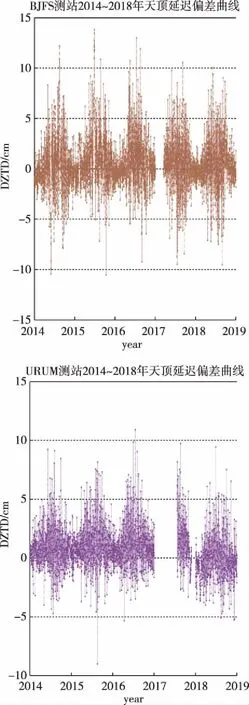
图4 GNSS测站2014—2018年天顶延迟偏差曲线Fig.4 Zenith delay deviation curve for GNSS measurement stations in 2014-2018

从图4中可以看出，BJFS测站偏差分布呈现季节性变化，全年变化较为平稳；URUM测站在2017年缺失了部分数据，其偏差分布规律总体与BJFS测站一致。但BJFS测站与URUM测站的ZTD偏差有部分超过5cm。为了探究该情况出现的原因，绘制BJFS测站和URUM测站的ZTD偏差与测站的高程差的对比图如图5所示。

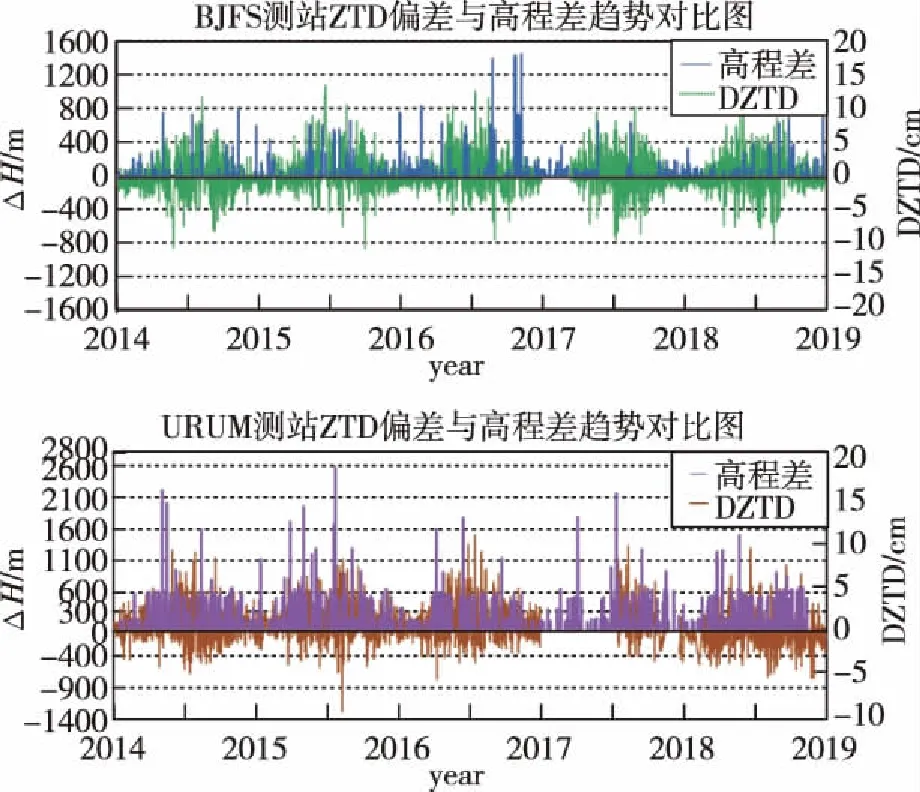
图5 ZTD偏差与高程差趋势对比图Fig.5 Comparison of ZTD deviation and elevation difference trend

从图5中可以看出，ZTD偏差与测站的高度差具有一定的相关性。在一定范围内，将GNSS的气象观测值作为起始数据可以弥合探空测站的数据；但当测站的高度差过大时，将GNSS的气象观测值作为起始数据则不能完全代替探空测站的数据。为了进一步探究这种现象出现的原因，绘制ZTD偏差和探空测站最大高度的对比图如图6所示。

图6 ZTD偏差与探空测站最大高度趋势对比图Fig.6 Comparison of ZTD deviation and maximum elevation trend by radiosonde station

从图6可以看出，ZTD偏差与探空测站可观测的最大高度也具有一定的相关性。由于探空数据中缺失对流层顶以上的观测数据，但对流层顶以上高度水汽值可以忽略不计，故本文利用Saastamoinen干延迟模型估算探空产品对流层顶以上的ZTD以弥补探空观测值的不足。尽管Saastamoinen干模型精度很高，但本身也存在一定的误差，尤其在较高的大气层上利用Saastamoinen干模型估算ZTD的精度还有待进一步研究。

为分析GNSS精密单点定位技术获得ZTD的精度，分别统计了4个IGS测站与探空测站估算ZTD的偏差及其他指标如表2所示。

表2 探空测站获得的ZTD与GNSS估算的ZTD之间偏差的统计值Tab.2 Statistical value of deviation between ZTD obtained by radiosonde station and ZTD estimated by GNSS cm

表2分别记录了二者偏差的Rms、Mean、Max及Min。从表2中可以看出，4个测站均方差均小于4cm，均值小于2cm，但最大值和最小值差异悬殊。为了分析偏差随季节的变化规律，下面进一步分析，以BJFS测站和URUM测站为例，计算2014—2018年每个月份偏差的均方差，结果如图7所示。

图7 ZTD均方差(RMS)随月份变化图Fig.7 Variation of ZTD mean square error(RMS) with month

从图7可以看出，ZTD的季节性变化明显，夏秋季节ZTD的均方差明显高于春冬季节ZTD的均方差。这说明夏季空气中的水汽含量较多，GNSS精密单点定位技术估算ZTD的精度受季节影响明显。

4 结论

本文将无线探空产品获得的ZTD作为真值评估GNSS精密单点定位获得的ZTD的精度，利用GNSS气象观测值来弥补探空测站与GNSS测站高程的不匹配。选取中国地区4个IGS观测值及其附近的探空测站2014—2018年的数据进行试算和分析，得到如下结论：

1)从精度分析结果来看，GNSS测站实测天顶延迟与探空测站天顶延迟偏差的Rms值小于4cm;

2)从空间分布来看，SHAO测站的Rms略大于其他测站的Rms，这与上海沿海的地理环境有关;

3)从时间分布来看，GNSS精密单点定位技术估算的ZTD精度受季节影响明显，春冬季节的解算结果精度优于夏秋季节的解算结果;

4)从数据处理来看，探空测站的数据精度与探空测站的测量垂直高程范围有关，另外，在较高的大气层上利用Saastamoinen干模型估算ZTD的精度还有待进一步的评估。