基于分形维数和模糊-A*算法的移动机器人路径规划研究
2022-11-10李绪王慧娜邓三鹏祁宇明李辉
李绪,王慧娜,邓三鹏,祁宇明,李辉
(1.天津职业技术师范大学机器人及智能装备研究院,天津 300222;2.天津市智能机器人技术及应用企业重点实验室,天津 300350;3.天津博诺智创机器人技术有限公司,天津 300350)
0 引言
移动机器人的实际工作环境信息复杂多变,仅依靠单一算法规划路径无法最佳满足应用场景的要求,移动机器人在规划全局最优路径的同时,更要具备动态避障的能力[1]。因此,多种路径规划算法之间融合,是目前路径规划的主要研究方向之一。
时也[2]针对A*算法转折次数过多,路径不平滑,引入了模糊算法,采用双层栅格地图,优化局部路径的平滑度,但是未考虑动态和复杂障碍物的情况。王洪斌等[3]利用二次A*算法与动态切点调整法优化路径的平滑度,结合改进的A*算法和改进的人工势场算法规划局部路径,解决了传统算法计算量大,效率不高等问题。Ji等[4]提出一种基于优化A*算法和动态窗口法的优化算法,提高搜索效率,但存在速度震荡的问题。
对已有的路径规划算法的研究中发现,A*算法具有运行速度快、路径规划短等优点,但是A*算法规划的路径拐点过多,路径也沿着障碍物的边缘前进。模糊算法在规划路径时,规划的路径是一条相对平滑的路径,但所规划的路径往往并不是最短路径。如将两种算法的优点结合起来而进行路径规划,可为移动机器人规划出一条平滑可行的最佳路径。使用A*算法对移动机器人进行全局路径规划,同时结合模糊算法进行局部规划,提高路径平滑度。引入分形维数,评估移动机器人路径的复杂程度,确保其在最佳路径轨迹下运行到目标点。
1 A*算法的描述
1.1 路径规划中的环境模型
要使用A*算法进行全局路径规划首先需要构建环境地图,通过构建已知的移动机器人工作环境地图才能有效地为移动机器人找到最佳路径。栅格地图中障碍物用黑色栅格表示,可通行区域用白色栅格表示。栅格法可随机产生障碍物的分布和数量,适用复杂环境的描述。
通过16×16的栅格图法来构建环境地图,对障碍物及边界区域的栅格进行赋值,将障碍物信息在栅格环境地图中显现,确定环境地图的环境边界、障碍物、起始点及目标点,黑色部分包含障碍物和边界。栅格地图如图1所示。

图1 栅格地图
1.2 A*算法
A*是一种启发式的路径搜索方法,它通过评价函数包含的启发信息快速锁定目标方向[4]。评价函数的一般形式如(1)式:

其中,f(n)是从起点经过节点n到终点的估价函数,表示节点n到终点的总体代价值。g(n)是起点到节点n所经过路径的实际代价值。h(n)是启发函数,表示节点n到终点的预计代价值。h(n)直接影响算法的成功率。故h(n)的选择对于整个算法至关重要。
所用的启发函数h(n)为曼哈顿距离:
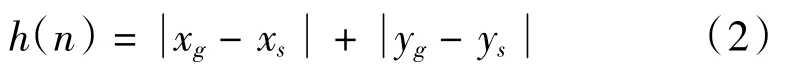
其中,xg和yg表示目标点的横纵坐标,xs和ys表示当前点的横纵坐标。
1.3 分形维数
目前有许多维数的定义和计算方法,主要包括豪斯多夫维数、盒维数、关联维数、容量维数等多种分形维数[5]。其定义为用边长为ε的正方形去覆盖平面所需要的正方形的个数为N(ε),公式可得:

式中,D代表盒维数。
盒维数运行速度快,占用内存少,利用栅格地图规划的路径是一维线性的,所以采用盒维数评估规划路径的复杂度。
2 融合算法
2.1 模糊启发式函数
融合算法通过A*算法规划出安全可通行的全局路径,在遇到障碍物时,通过引入模糊算法,增强h(n)启发性。设计的模糊启发式函数h’(n)为

其中,(1+m)为模糊因子,m的值为5×5栅格中障碍物占地面积与5×5栅格总面积的比值,取值区间为[0,1]。
以A*算法规划的全局路径为指引,融合模糊算法实现移动机器人的避障,从而保证移动机器人路径规划的有效性与安全性,同时引入分形维数,评估路径的复杂程度。
以5×5栅格作为一个分形维数评估区域,如图2所示,通过判断这5×5栅格中路径的盒维数,来评估5×5栅格区域中路径的复杂程度。

图2 5×5评估区域
融合算法首先通过A*算法规划出安全可通行的全局路径,在遇到障碍物时,通过模糊算法规划局部路径,使移动机器人进行避障。最后通过分形维数来评估规划出路径的复杂程度。融合算法流程图如图3所示。
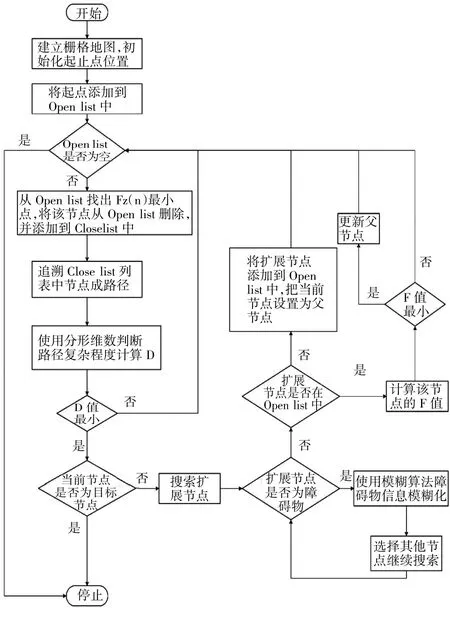
图3 算法流程图
2.2 基于模糊算法的移动机器人避障
将移动机器人的左侧、前方、右侧与障碍物的距离LD、FD、RD,以及移动机器人当前的运动方向与目标方向的夹角θ及当前速度v作为模糊控制的输入,将移动机器人左右轮加速度a1和ar为模糊控制的输出。将距离输入模糊语言定为{NEAR,FAR};将移动机器人运动方向与目标方向夹角θ模糊语言定为{LEFT,FRONT,RIGHT};将当前速度v模糊语言定为{SLOW,FAST};将移动机器人左右轮加速度模糊语言定为{NB,NS,Z,PS,PB}。下面列举部分模糊控制规则库,如表1所示。
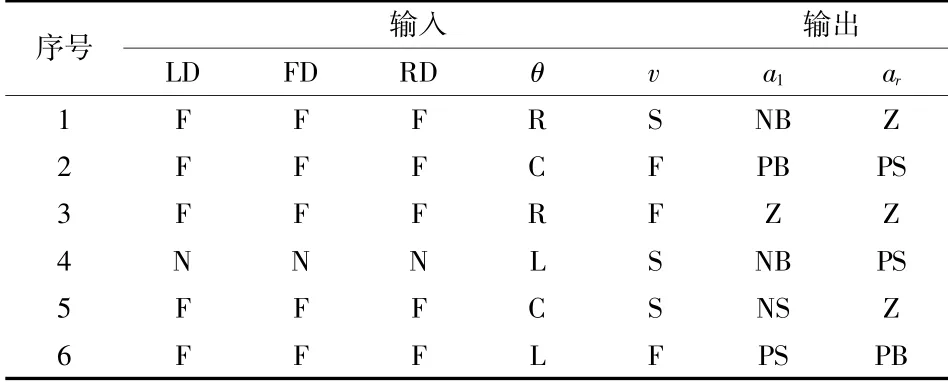
表1 模糊规则库
在此使用Mamdani推理,用质心法去模糊化,最终得到移动机器人所需的加速度。
3 仿真实验与分析
为检验算法的性能,在Intel(R)Core(TM)i7-7700HQ CPU@2.80GHz计算机上利用MATLAB 2020b对模糊算法、传统A*算法和融合算法在相同的栅格地图场景中进行仿真验证。构建了一个16×16环境栅格地图,模糊算法、传统A*算法及融合算法的仿真实验结果,如图4所示。

图4 算法仿真对比图
图4中浅灰色小正方形为起始点,起始点为(1,1),深灰色小正方形为目标点,目标点为(15,15),黑色栅格为障碍物。对比图(a)、图(b)和图(c)可以看出,融合算法中移动机器人路径更加平滑,冗余点及拐点也更少。因此,融合算法在移动机器人路径规划的实际应用中,具有更高的安全性。三种算法在路径规划时的相关参数见表2。
通过分析表2中相关参数,融合算法比其他两个算法更加优越,主要表现以下方面:路径距离减少了38.49%,拐点数减少了66.67%,同时路径平滑度(拐角)提高了66.67%。以上数据充分证明融合算法在移动机器人路径规划时,规划出的路径更平滑,距离较优,更适合移动机器人日常的工作。

表2 三种算法相关参数
4 结语
基于分形维数的模糊-A*控制算法的移动机器人路径规划方法,对A*算法进行改进。引入模糊算法,优化路径平滑度,减少路径转折点,与障碍物保持一定的安全距离;引入分形维数,进一步优化路径。通过实验结果表明,基于分形维数和模糊-A*算法能够使移动机器人避开触碰障碍物,运动路径更为平滑,节点数明显减少。
