基于多传感器融合的机器人编队ADRC控制

毛文勇，仇 翔，张文安

(浙江工业大学信息工程学院，杭州 310023)

0 引言

近些年，随着机器人和人工智能的快速发展，机器人领域的变化趋势也从固定的机械装置向能够做更多复杂任务的自主移动机器人过渡。如未知环境探测、远程医疗、物流、服务业等领域［1-2］。移动机器人控制系统是一种非完整系统，其控制问题一直是个难题，而其中的编队控制更是移动机器人控制中的关键问题之一。

在移动机器人的编队问题的研究已经有许多研究成果。例如，利用李亚普诺夫函数设计速度误差控制规律，实现目标位置的跟踪控制。但是缺点在于动态控制器过于理想化，在实际中很难实现［3］。智能控制律被用于多智能体系统，并实现了同步跟踪［4］。神经网络控制方法虽然具有学习能力，但学习速度慢，神经网络结构选择复杂［5-6］。此外，还有基于行为的方法［78］、虚拟结构法［9］、领航跟随法［10-11］以及其他智能控制算法［12］。尽管轨迹跟踪问题已有大量研究结果，但多数结果只是依靠仿真来验证算法的有效性。在实际应用中，就需要考虑更多因素，例如如何提高移动机器人定位精度从而提高轨迹跟踪控制精度，其次，由于环境的未知，干扰的不确定等因素都会对控制方法的实际实施效果产生影响，需要提高控制方法的鲁棒性。在移动机器人编队完成特定的任务工作时，队伍中的个体移动机器人需要知道其他移动机器人的位置信息，目前在这方面的研究也需要加强。

为此，本文采用融合激光传感器和里程计数据的方法提高移动机器人定位精度，进而采用自抗扰控制技术实现主从式移动机器人编队跟踪控制，提高了移动机器人编队控制系统对运动环境不确定性的鲁棒性。最后，利用三台轮式差速移动机器人设计了主从式移动机器人编队控制实验系统，并在该实验平台上验证了所提出算法的有效性和优越性。

1 移动机器人轨迹跟踪误差模型

本文实验所有的移动机器人考虑的是两轮差速轮式移动机器人。为了建立移动机器人的数学模型，简化机器人的机械结构，得到如图1所示的差动机器人简易模型。如图1所示，差动机器人具有独立驱动的左轮和右轮，然后再配备一个万向轮保持平衡。

对图1中的符号作如下说明:

V(t):移动机器人移动线速度

w(t):移动机器人移动角速度

VL(t):移动机器人左轮相对地面的移动线速度

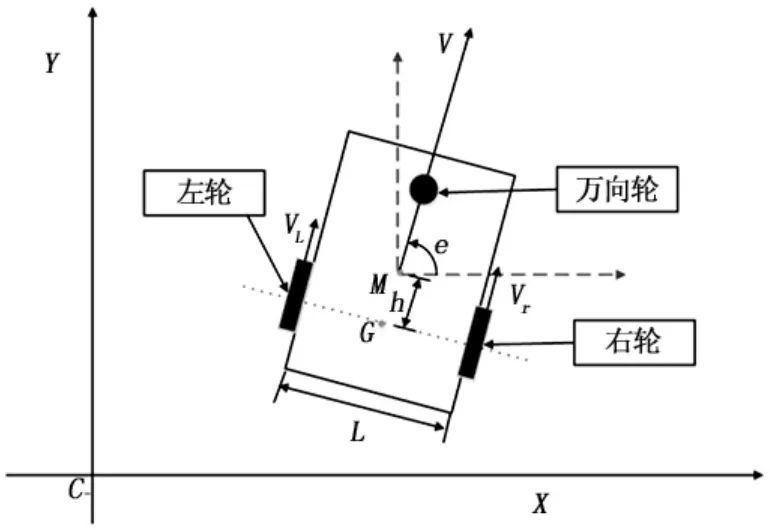
图1 两轮差动驱动移动机器人模型示意图

Vr(t):移动机器人右轮相对地面的移动线速度

θ(t):移动机器人X轴正方向的夹角，即航向角

x(t):移动机器人X轴坐标

y(t):移动机器人Y轴坐标

M:移动机器人质心点

G:移动机器人两轮中点

L:移动机器人两轮之间的距离

H:移动机器人G点与M点之间的距离

假设1:机器人的质地均匀，质心为几何中心点，且机器人运动过程中左右两轮与地面纯滚动无滑动。

基于该假设，移动机器人的运动学模型可描述为:

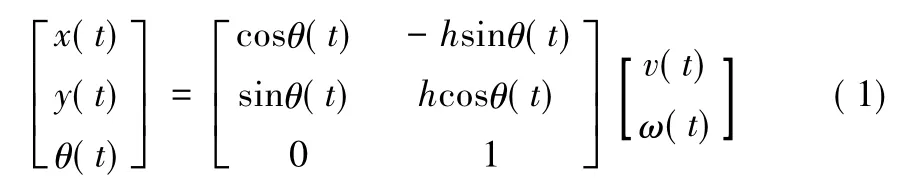
当移动机器人在做转向运动时，其瞬时运动可以近似为直线运动。假设采样时间为△t，获得机器人的里程计模型:

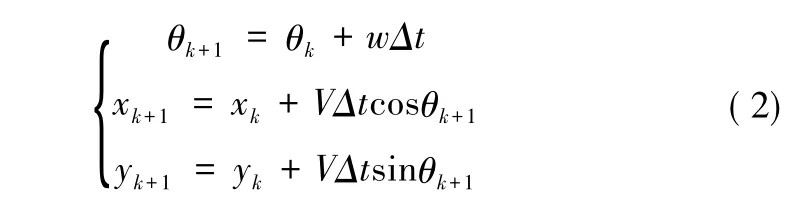
如此就可以根据根据里程计模型实时估算机器人的位置信息。本文考虑的移动机器人编队问题指的是各个跟随机器人以恒定的横向距离以及纵向距离跟踪主移动机器人的运动。因此，需要描述每个从机机器人与主机器人的跟随误差模型。其中，MR代表主移动机器人，S1，S2分别代表两台从机器人。因为每台从机器人与主机器人建立的误差模型都是一样的，下面仅由SR代表从机器人。

现根据MR和SR各自的动态里程计模型，对机器人编队系统的位置偏差和角度偏差进行分析。记ex和ey为主从机器人之间的位置偏差，eθ为住从机器人之间的航向角偏差。这样建立主从机器人跟踪误差表示为:

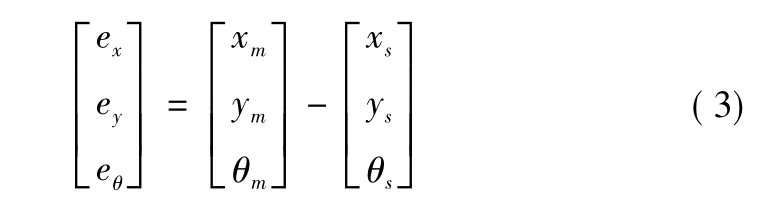
其中:xm，ym表示主机器人的位置信息，xs，ys表示从机器人的位置信息，θm表示主机器人的航向角，θs表示从机器人的航向角。实验中主移动机器人实时把自身的位姿信息发送给从移动机器人。

本文编队需要解决的问题是:当主移动机器人以额定的线速度和角速度移动时，从移动机器人能够快速的从起始位置跟踪上主移动机器人的状态。即以相同的线速度和角速度跟随主移动机器人移动，并且能够保持主从移动机器人之间的横纵距离为定值dqx和dqy。

肋拱施工是渡槽工程的关键部位，混凝土强度又是重中之重，而混凝土中间产品是最直接的反应。为此，首先为了掌握混凝土强度情况，在浇筑过程中制作多组混凝土抗压试件，测出肋拱混凝土3 d、7 d、28 d强度，并绘制出曲线图（如图2）。

2 移动机器人主从跟踪控制器设计

2.1 移动机器人定位算法

多传感器融合是把在不同位置的多个不同传感器所提供的局部环境的不完整信息加以融合。消除传感器之间可能存在的冗余信息。多传感器融合的理论就是更加精准的反应环境信息。目前在工业、军事等众多领域有了广泛的应用。

从上述可知移动机器人能够通过电机编码器依据公式(2)估算出移动机器人的当前位姿。然而在实际应用中，由于轮子打滑等因素会导致定位精度降低。从式 (2)可看出里程计估算会导致测量累积误差，从而导致定位结果有较大的偏差，这将给后续的轨迹跟踪控制带来较大影响。为此，本文采用多传感器融合［13-14］的方法来提高定位精度。基于里程计和激光传感器融合的移动机器人定位方法由以下算法给出。

首先，通过在线读取安装在左右驱动电机上的码盘测量并计算出机器人左右轮的线速度。进而依据式 (2)和采样周期Δt推算出当前移动机器人的位 置和航向作为估计值。为此，定义状态变量［x y VxVy］，系统的状态方程为:Xk+1=ΦXk+Wk。其中x和y表示移动机器人在全局坐标系中的坐标值;Vx和Vy分别是x轴和y轴方向的移动速度;Φ为tk时刻到tk+1时刻的状态转移矩阵，表达式见式(3);Wk是协方差为Q的系统噪声矩阵。

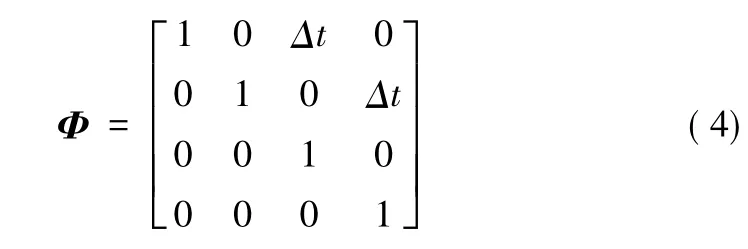
其次，依据激光传感器测得移动机器人位置数据作为测量值，为此，定义系统的测量方程为:Zk=Xk+Vk。其中，Xk是激光测得的移动机器人位置数据;Vk是协方差为R的系统测量噪声矩阵。

最后，通过下面步骤一到步骤五反复迭代更新移动机器人位置信息。

步骤一:由前一时刻的位姿 Xk|k通过式 xk+1|k=Φk+1|kxk|k预测新的状态值Xk+1|k。

步骤二:由上一次的误差协方差Pk|k通过式pk+1|k=Φ+Q得到新的误差Pk+1|k。

步骤四:通过式xk+1|k+1=xk+1|k+K(Zk－xk+1|k) 对步骤一的状态值Xk+1|k进行校正。

步骤五:为了下次预测的迭代操作，需要由式pk+1|k+1=(I－K)pk+1|k得到更新后的Pk+1|k+1值。

2.2 主从式轨迹跟踪的ADRC控制器设计

自抗扰控制技术作为一种新型的控制算法，发扬PID技术的精髓并且吸取现代控制理论。它不依赖被控对象精确的模型，能够对系统中存在的不确定干扰有很强的抑制作用。ADRC控制器主要由三部分组成:跟踪微分器(TD)、扩张状态观测器 (ESO)、非线性误差反馈控制律。本文机器人编队问题的关键在于各个从机器人与主机器人之间的距离控制。每个从机器人的输出是每个从机器人的实际期望距离dx和dy。为了得到更为精准的控制结果。本采用自抗扰技术对系统加以控制。由于主从移动机器的跟随误差模型是一阶系统，因此自抗扰控制器设计主要包括两个部分，忽略了跟踪微分器。第一部分是扩张状态观测器，主要是得到主从移动机器人的横向距离跟踪值dx以及纵向距离跟踪值dy，还有就是总扰动的实时估计值fx和fy。

以横向间距为例，纵向间距的跟踪模型可类似得到。扩张状态观测器表示为:

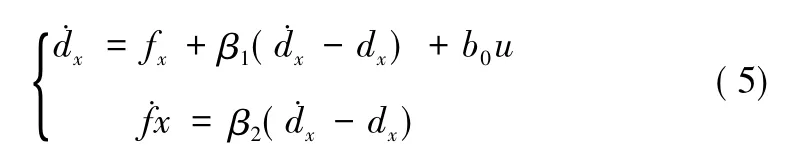
第二部分为控制规律的设计，具体的形式如下:

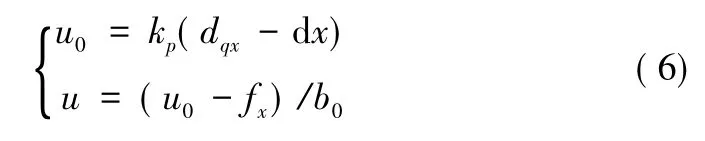
利用自抗扰技术为编队中每个跟从移动机器人的跟随控制系统设计两个ADRC跟踪控制器，其具体的控制框图如图2所示。

图2 ADRC的系统结构图

假设:移动机器人在纯滚动无打滑条件下运动的，移动机器人线速度为v，角速度为ω，左轮速度为vl，右轮速度为vr。

移动机器人直线运动时:有vl=vr=v。

移动机器人非直线运动时，视其小范围内运动用半径为R的圆代替，则有:

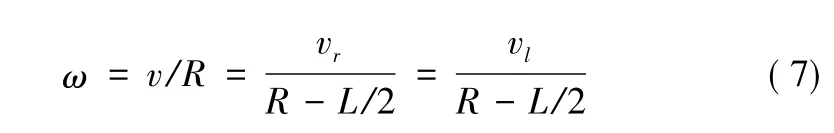
可得:

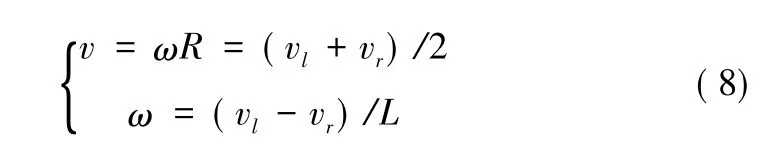
这样就可以实现移动机器人左右轮线速度与移动机器人移动线速度与角速度之间的转换。

3 实验与结论

在实验中，为了能够简化驱动程序编写，方便不同机器人之间的信息传递，机器人开发环境采用ROS操作系统［15-16］。此外，为了能够有良好的人机交互，将ROS与QT结合使用，编写上位机程序，直观的实时体现机器人的动态性能。首先为每台机器人建立/Robot、/serial_node两个节点。主机的/MasterRobot节点分别订阅激光节点/hokuyo_node的/scan话题、/serial_ node节点的/M1Speed和/M2Speed两个话题。/MasterRobot节点在线实时得到/scan的激光数据、/M1Speed的左轮线速度、/M2Speed右轮线速度并用上一节提出的卡尔曼滤波算法进行数据融合，得到精准定位信息，然后通过/odom话题把主机的位置信息发送给从机。从机通过在线接收来自主机的/odom话题包来获取期望位置。然后根据式 (3)误差模型分别得出横坐标和纵坐标的偏差值dx，dy。将两个偏差值运用各自的自抗扰控制器获取的控制量u。最终通过式 (8)算出左右轮的期望速度。每天从移动机器人发布/motorL和/motorR两个话题，上位机通过这两个节点向电机发送实时控制速度。由此，移动机器人每个周期通过传感器采集位姿信息，然后与期望位置作差值比较得出理想的线速度值传送给电机，如此反复更新速度数据来控制每个从机器人的最终位置。

本实验用三台移动机器人进行编队实验。一台主移动机器人:以导航机器人的身份存在，主要任务是带领其他从移动机器人运动。两台从移动机器人:以跟随者的身份存在，主要任务是通过上面设计的自抗扰控制器进行跟随编队实验，验证所提算法的鲁棒性。实验时，场地为已知边界的室外环境。主移动机器人所处的位置设定为坐标轴的原点 (0，0)，将一台从机器人放置在主移动机器人左侧 (－0.3，0)出，定这台从移动机器人为S1，再将另外一条移动机器人放置在 (－0.6，0)出，定为S2。实验过程中运动方式为:主移动先做直线运动，在经过一定时间后，改变运行状态，做弧线运动。一台从移动机器人以dx=0.3，dy=0.3与主移动机器人保持同步运动，另一个台从移动机器热以dx=0.3，dy=－0.3与主移动机器人保持同步运动。两台移动机器人从初始位置快速跟踪到期望偏差位置，在这过程中每台从移动机器人 (跟随机器人)通过ROS节点实时得到主机的位置信息，然后进行跟随控制。上位机实时记录主从移动机器人的轨迹信息。图3显示为机器人编队中每台机器人在自抗扰技术控制下的跟随轨迹。图中，绿色线表示一号从移动机器人，蓝色线表示二号主移动机器人，黄色表示三号从移动机器人，红色线表示期望轨迹。为了方便观测，图中的曲线是经过平移显示的。

图3 主从机器人轨迹图

以下将给出在自抗扰技术下实验得出的结果。在整个编队试验过程中记录编队中所有移动机器人的横坐标x，纵坐标y以及实时运动速度v。自抗扰控制器中，各个参数在试验过程中具体数值为:

ADRC_X(横向距离):Kpx=1．3，b0x=2，β1x=100，β2x=1 000

ADRC_Y(纵向距离):Kpy=2，b0y=4，β1y=200，β2y=1 000

将记录的数据进行分析，得到图4机器人实时速度对比，图5机器人x轴跟随情况，图6机器人y轴跟随情况。

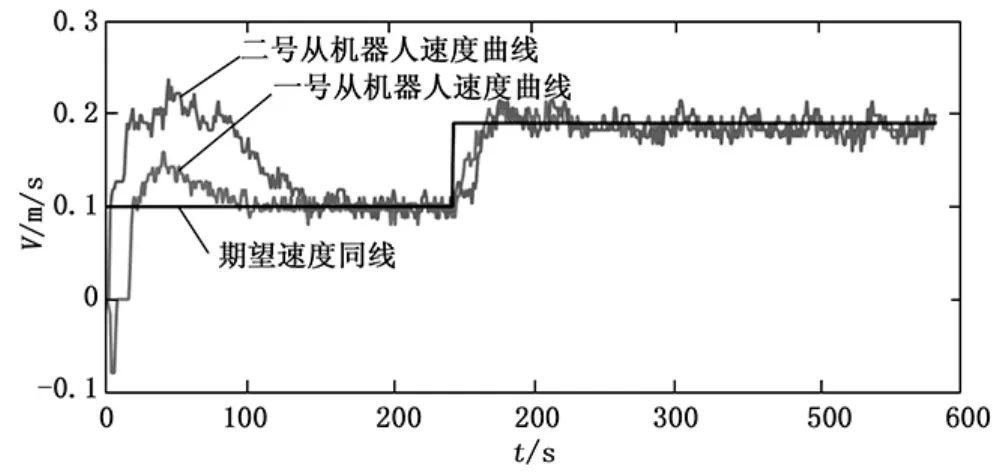
图4 机器人实时速度对比

图5 机器人x轴跟随情况

图6 机器人y轴跟随情况

本文研究了移动机器人的编队问题，运用先进的自抗扰技术，设计了特定的自抗扰控制器。并且通过搭建移动机器人编队实验平台验证了所提算法的鲁棒性。在实验时，两台从移动机器人的起始速度为0，当主移动机器人以0.1 m/s的速度匀速直线运动时，两台从移动机器人快速实现跟踪。而且从图4两台从移动机器人的速度响应曲线可以看出，两台移动机器人不仅能够快速的响应到主机的运动速度并且稳定在0.1 m/s上下波动。还能在主移动机器人运动状态发生改变后，每台从移动机器人还是能够快速稳定到期望的速度位置。从移动机器人的坐标信息来分析。上述我们假设过主机的位置为 (0，0)。由于一号从机器人的初始位置为 (－0.6，0)，但是要保持与主移动机器人dx=0.3，dy=0.3的间距的同步运动。因此首先需要快速跟踪到主移动机器人的当前位置，这也解释了图4中一号从移动机器人在起始阶段速度大幅度提升，而后续逐渐平稳。从图5也可以看出一号移动机器人由－0.3逐渐平稳的跟随主机移动，即使中间段有一部分主机改变运动状态也能较好的重新达到稳定状态。相应的，从图6也可以得出二号从移动机器人相识的结论。通过上述的分析结果表明:本文所设计的自抗扰控制算法能够较好的抑制外部干扰的影响并且对不可比避免的内部干扰予以补偿。算法具有较高的鲁棒性和较好的控制精度，很好的实现文章开始提出的移动机器人编队控制。