考虑框架协议的动态报童模型强化学习建模研究
2022-11-10祁玉青赵兴雷赵田东杰
祁玉青, 赵兴雷, 赵田东杰
(南京工业大学 经济与管理学院,江苏 南京 211816)
0 引言
采购框架协议是指企业为了稳定货源、减少采购谈判等成本,与供应商签订一定时期内的协议,约定该时期内的采购数量、价格、质量等细节[1]。其中最常见的协议是约定零售商在协议期内订购产品总数不能低于协议订货数量,供应商在协议期内向零售商及时供货,不能因缺货造成零售商的损失。框架协议模式下的采购决策本质是一类带有约束条件的库存优化问题。
报童模型是随机库存决策的一个基础性模型[2]。约束条件下的报童问题也已有广泛研究。各约束条件包括:预算约束、订购量约束、库存空间约束、地点约束等。但在报童产品背景下,采购协议下的库存模型较为缺乏。对于报童问题的研究,从单周期背景出发建模的文献居多,但在考虑一定时期内的预算约束,供应商能力约束等情形下,从周期背景出发进行建模也是研究的一个重要方向。在对多周期报童问题研究中,Zhang等[3]提出基于拉格朗日松弛的方法解决存在数量折扣的多周期多产品获取规划问题。Li等[4]利用弱聚合算法研究考虑短缺成本和整数订购量的多周期报童问题。Puranam等[5]研究区域血液交换网内大型医疗中心对红细胞的管理问题,提出了求解方法,并利用动态程序求解多周期成本最小化问题。
框架协议下研究订货策略的文献有,Chen等[6]研究总订单数量承诺合同,提出了双订货至订货水平的最优库存补充策略。Cai等[7]在两级供应链承诺订单合同下,研究零售商承诺订单数量对供应商投入数量决策的影响,发现承诺订单契约能刺激供应商投入产量。Wang等[8]研究一个零售商面对两种供应的选择问题,开发了一个启发式系统,证明了公司忽视或过分强调订单承诺会造成损失。但一些订货策略在针对销售期较短、带有明显季节性和周期性波动的报童产品问题上并不适用,零售商传统的做法是采用预测方法进行预测。
强化学习(简称RL)是机器学习的一种重要方法,通过智能体与环境的交互过程学习策略实现特定目标。利用强化学习求解决策问题的研究有,蒋国飞等[9]将一种新的探索策略和强化学习Q学习算法结合求解一类有连续状态和决策空间的库存控制问题,证明了Q学习算法应用潜力。郑江波等[10]针对零售商在销售易逝品时的联合决策问题,提出运用马氏决策过程建立模型及使用Q学习算法求得最优策略。Kara等[11]以总成本最小为目标,利用Q学习算法研究随机需求和确定交货期条件下易腐产品库存决策问题。
基于强化学习处理动态、多阶段问题的优势及补充现有研究,本文在随机生成样本数基础上,运用强化学习Q学习算法求解协议下库存模型,通过数值实验验证强化学习解决框架协议报童问题的有效性。
1 框架协议下的库存决策模型
1.1 问题描述与分析
考虑零售商销售某报童产品,销售周期无限,协议期有限,当天订购的产品若未售出,则第二天不能继续销售,未售出的产品会产生残值。零售商在销售前订购当天产品。在协议期内,产品的售价和残值不变。
以n天为一个协议期,在第一天销售开始前当天产品订购数量已定,当天销售开始后,对于需求量大于订购量的情况,利润为订购量*(售价-成本)-当天订购成本;需求小于订购量时,利润为需求量*(售价-成本)-当天订购成本+残值*(订购量-需求量)。完成当天工作后,进入下一天销售状态。零售商在协议期内订货量首先要满足协议量。协议期最后一天如未满足协议量则当天订货量即为剩余协议量的数量,如果满足协议订货量,以原来方法订货。
1.2 符号说明及相关假设
模型中所用的相关符号说明如下。

表1 模型中相关符号的解释
考虑模型的普适性,本文假设如下:
①产品的成本和销售价格是恒定的。
②当天未售出的产品第二天不可销售,但会产生残值。
③报童产品不产生相应的存储费用。
④每天的需求为di,i=1,…,n,di服从随机分布。
⑤没有初始库存,每天必须订购产品进行销售。
⑥成本方面只考虑销售额、订购成本、残值。
1.3 模型构建
图1表示协议期内每天的状态,以订货阶段为起点,零售商向供应商进行订货,决定订购数量。接着进入销售阶段开始销售,当一天的销售状态结束时,得到相关销售量信息。结算阶段可根据销售额以及订购成本等计算当天的利润。基于上述,本文以总利润为标准建立模型。

图1 协议期内每天的状态
协议订货量约束k与采购单价c相乘,可得协议订货总金额,在协议期内零售商的订购金额不能低于这个协议订购金额C。C是与k相关的一个函数。即
C=C(k)=ck
(1)
xi=p×min(qi,di)
(2)
(2)式表示第i天销售额xi,当第i天订货量大于需求时,销售额为售价×第i天需求;当第i天订货量小于需求时,销售额即为售价×第i天的订货量。
yi=c×qi
(3)
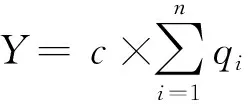
(4)
Mi=m(qi-di)+
(5)
fi=xi-yi+Mi
(6)
fi=pmin(qi,di)-cqi+m(qi-di)+
(7)
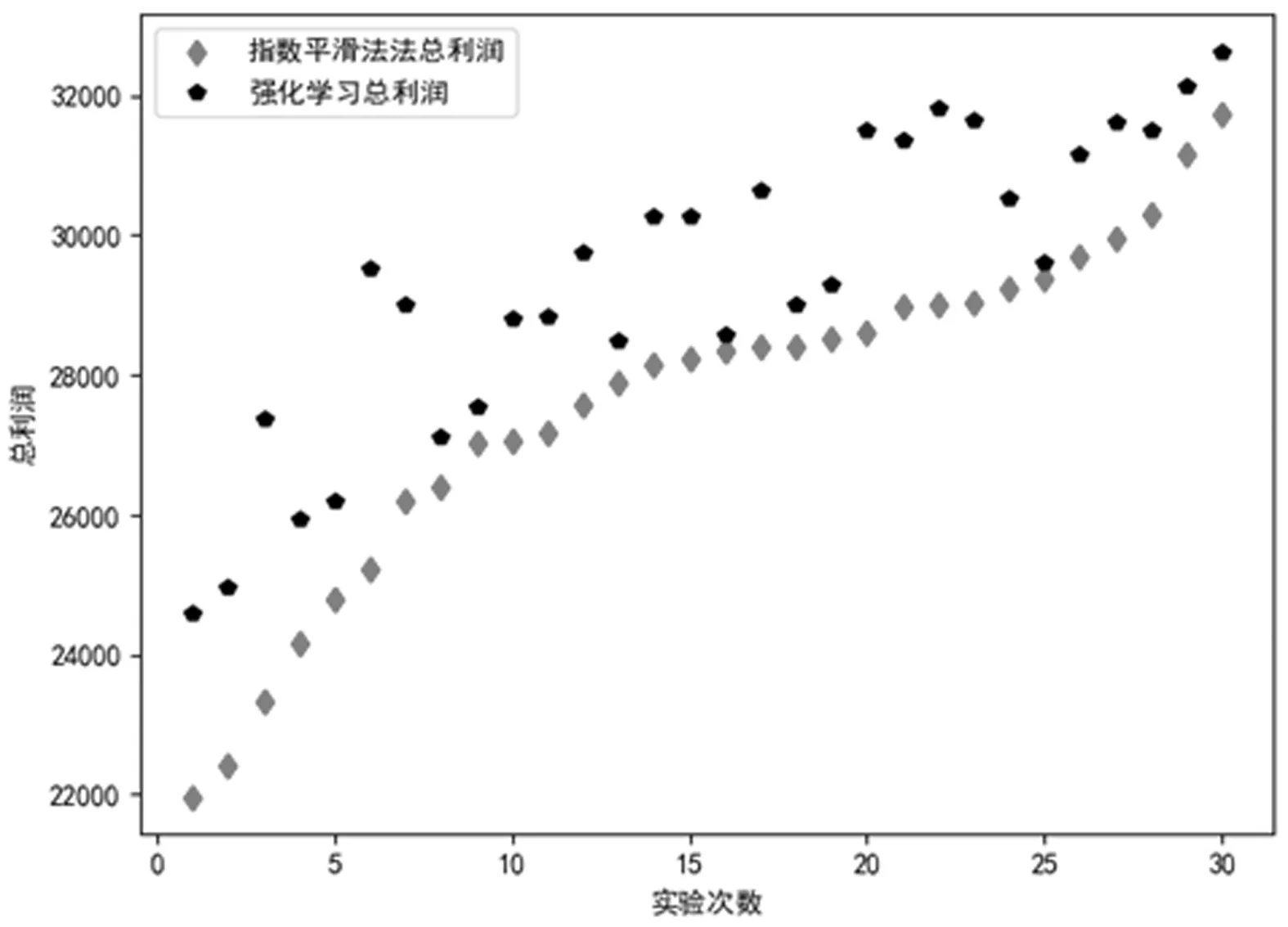
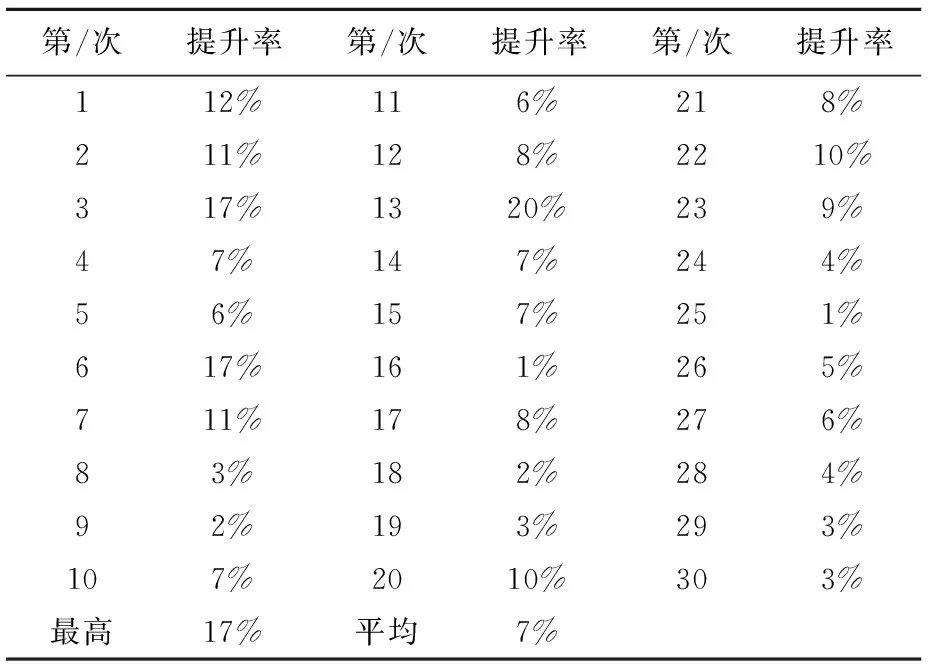
(5)式中,Mi表示第天未售出产品的残值,当qi>di时,取差值与单位残值相乘;qi (8) (9) 模型(9)中可行解和可行集的数量受到di的影响,还受到协议的约束。本文采用库恩-塔克(简写为K-T)条件对其分析,假设需求量(为便于表述用x表示,即上述d=x)为连续随机变量,其概率密度为f(x)。 考虑约束问题时,可考虑将约束问题转化为无约束问题。式(10)为优化问题的目标函数,优化问题约束条件本质受到协议订货量的约束,约束写为g(q*)。 (10) (11) 设q*∈S={q|gi(q*)≥0,i=1,2,…,m)},如果在q*处,gi(q)可微,那么满足式(12)条件的点称为K-T点,即最优点。对目标函数和约束条件分别求导得到式(13)(14),代入(12)中,可得到式(15)。分析可得出以下性质。 (12) (13) (14) (15) (16) (17) 满足式(17)的q点是最优订货点,订购量q受到需求量x、协议期长n的影响,由于协议期长n与协议订购量有关,q也受到协议订购量k的影响。 但在实际生产经营中,需求量有着不确定性,并且实际订货量不会一直等于协议订货量,因此传统运筹学求解有较大困难。在针对类似问题(9)求解上,有学者做了相关研究。Karl等[12]用动态规划推导采购策略结构,用启发式方法确定政策参数处理多周期问题。Wang等[8]也使用启发式方法,开发了一个启发式系统解决零售商对订货承诺选择问题。禁忌搜索[13]和遗传算法[14]方法也被用于求解。多数求解方法是使用算法逼近最优值。求解上述问题时,最优策略求解复杂且困难。徐翔斌等[15]提出在研究多阶段决策问题上,强化学习能克服传统运筹学建模方法的缺点,可以通过Agent与环境不断交互,学习到策略;在难以求解的动态性与随机型问题上,有相应优势。另外有学者用强化学习算法处理单阶段库存问题[11]、动态性和非稳定需求问题[16,17]获得了较好的效果。综合上述,本文使用强化学习来进行建模求解。 强化学习是通过智能体Agent对环境st的感知,采取既定的策略at,获得执行at后的奖赏rt,环境发生改变,进入到下一个状态st+1。目的是让Agent在环境中学习到一种策略,在策略指导下,获得最大的奖赏。 图2 强化学习流程图 图2是强化学习的流程图,在每天决策时,零售商的订货量和产品需求量构成一个状态,即状态st,零售商要根据相应的状态做出订货决策,即动作at,那么每次采取何种策略(π)是由于s→a所决定,即根据所处环境(状态)做出动作。本节对相关符号解释如表2所示。 表2 强化学习中相关符号的解释 引入Rt和折扣因子γ。式(18)为强化学习整个过程的Rt,Rt为各个行动的rt与相应折扣因子乘积的累加。零售商每天的利润等于每个状态下采取行动的奖赏即ft=rt,如式(19)所示。本文所要研究的是利用强化学习选择策略获得较大ft的总和F。 Rt=rt+1+γrt+2+γ2rt+3+…+γkrt+k+1 (18) Rt=ft+1+γft+2+γ2ft+3+…+γkft+k+1 (19) 最优策略对应的收益用状态值函数Vπ(s)表示,状态s表示天数。 Vπ(s)=E[Rt|st=s] (20) Vπ(s)=E[rt+1+γVπ(st+1)|st=s] (21) Vπ(s)=E[ft+1)+γVπ(st+1)|st=s] (22) Vπ(s)=E[pmin(qt+1,dt+1)-cqt+1+ m(qt+1-dt+1)++γVπ(st+1)|st=s] (23) 用状态值函数评估当前策略下的期望回报,如式(20)。式(21)是利用贝尔曼方程对式(20)进行的转变,其意义是当前状态值函数可通过下一状态值函数计算。库存问题的状态值函数,如式(22)(23)。 Qπ(st,at)=Eπ[Rt|st=s,at=a] (24) Qπ(st,at)=Eπ[rt+1+γQ(st+1,at+1)|st=s,at=a] (25) 引入状态动作值函数Qπ(st,at)表示智能体Agent在当前st状态下采取某行动at带来的回报,如式(24)所示。根据贝尔曼方程,式(24)转化为式(25)。 本文求解采用Q学习算法。Q学习是强化学习一种重要算法,能够针对状态转移概率和回报函数未知的情况,利用唯一可用的当期回报Rt学习策略,优化一个可迭代计算的Q函数。Q学习按照以下顺序进行:在t时刻,观察当前的状态st,选择并执行动作at,观察后续状态st+1,并获得回报Rt,通过式(26)不断调整t时刻的Q值,得到t+1时刻的Q值[9],进行下一动作,如此不断探索,直到所有状态结束。 Qt+1(st,at)=(1-a)Qt(st,at)+ a[Rt+γmaxQt(st+1,at+1] (26) 在算法训练过程中,通过式(27)更新Q-table。Q学习算法运行结束生成Q-table,Q-table是Q学习的核心,Q-table的行和列分别表示状态和行动的值,Q-table的值Q(s,a)能够衡量当前状态采取行动的效果。 Qπ(s,a)←Qπ(s,a)+α[R+γmaxQπ(s′,a′)-Qπ(s,a)] (27) 本文Q学习算法实施形式化过程如下: ①初始化设置,通过生成随机数来模拟需求数据,根据优化模型和几种订货方法计算利润值(奖励值),并建立初始Q-table。 ②设置参数,包括环境、动作、贪婪度、学习率、奖励递减值等;命名动作at,选定本文所要训练的订货方法产生的数据。 ③控制贪婪度ε,根据贪婪策略选择动作at-订货方法。 ④执行当前订货策略at,获得采取的订货策略奖励值,进入下一状态st+1,在状态st+1下进行策略at+1的选取,直到结束。 ⑤根据式(27)更新Q值、更新动作在Q-table中的Q估计值。 ⑥不断训练,满足终止条件时停止运行;若不满足,继续运行训练。 ⑦算法终止,得到最终Q-table。 本部分对几种方法所得利润进行比较,基于相关参数分析总利润的变化规律,得出结论。算法基于python语言运行。模型和算法中相关参数设定如表3所示。 表3 参数设定 根据上述,本文在其他条件相同情况下,分别求出几种方法订货的总利润并进行对比。 3.1.1 三种传统订货方法的对比 定量订货法即零售商在协议期内每天订购相同数量产品,其订购量在一定范围内随机生成。移动平均法是用最近实际数据预测未来一期或几期数据的方法,在实验中本文选择不同权重下移动平均法决策,并选取较大总利润数据。指数平滑法即考虑时间序列和过去数据的预测方法,基于不同权重利润比较本文选取0.5和0.7作为实验中指数平滑法的权重。 图3 三种传统方法总利润对比图 本部分对比三种传统订货方法在同等情况下产生的总利润,并以定量订货法总利润递增顺序对实验次序排序,如图3。对实验顺序重新排列,不会改变实验数据,也不会对结论造成任何影响。在所有的实验次数中,移动平均法和指数平滑法总利润都高于定量订货法总利润,这说明在相同条件下,采用前者进行决策更有优势。但移动平均法和指数平滑法总利润相差不明显,不能够对比哪种方法最优。 3.1.2 强化学习与定量订货法的对比 以定量订货法总利润递增顺序对实验次序排序,如图4。横纵坐标分别表示试验次数和总利润,红色菱形表示定量订货法总利润,黑色星形表示强化学习总利润。表4统计了强化学习相比定量订货法利润提升率。与定量订货法相比,使用强化学习方法决策可大幅度提升利润,多次实验平均利润提升率达到22%,单次最高利润提升率达47%,表明利用强化学习进行决策能够帮助零售商在满足协议下提升利润。 图4 强化学习与定量订货法总利润对比图 表4 强化学习相比定量订货法总利润提升数据表 3.1.3 强化学习与移动平均法的对比 图5对比了强化学习与移动平均法多次实验的总利润,红色菱形表示移动平均法总利润,黑色星形表示强化学习总利润,以移动平均法总利润递增顺序对实验次序排序。表5中,多次实验下强化学习总利润高于移动平均法总利润,平均利润提升率达到8%,单次最高利润提升率达18%,虽然低于3.1.2部分的利润提升率,但仍有较大程度提升,相比移动平均预测,强化学习有着更好的优势。 图5 强化学习与移动平均法总利润对比图 表5 强化学习相比移动平均法总利润提升数据表 3.1.4 强化学习与指数平滑法的对比 图6对比强化学习与指数平滑法总利润,红色菱形和黑色星形分别表示指数平滑法和强化学习总利润,以指数平滑法总利润递增顺序对实验次序排序。表6统计了强化学习相比指数平滑法的利润提升率。多次实验下平均利润提升率达到7%,单次最高利润提升率达17%,另外与3.1.3部分结果相差很小,这一方面体现了移动平均法和指数平滑法的相似性,也表明强化学习相比传统决策方法的优势,在解决特定库存问题上具有优越性。 图6 强化学习与指数平滑法总利润对比图 表6 强化学习相比指数平滑法总利润提升数据表 3.1.5 强化学习与理想化状态的对比 本文计算了理想状态下总利润,理想状态是所有的订货周期发生完毕后所能观察到的最优策略,这是一种理论上的最优策略,由于需求的不确定性,现实经济环境中的订货策略只能无限接近理想状态。 图7是多次实验中Q学习算法总利润和理想化状态总利润对比图。黑色菱形代表理想化状态总利润,红色星形代表强化学习总利润。以强化学习总利润递增的顺序对实验次序排序。 图7 强化学习与理想化状态的总利润对比图 可得结论:①强化学习利润接近于理想状态利润,Q学习算法对数据不断训练、不断学习能够选择更优策略。②用强化学习考虑库存决策问题是有效的,能够提高利润。根据表7,与理想状态平均总利润差距在8%,强化学习总利润接近理想化状态总利润,验证了强化学习方法的有效性。 表7 强化学习相比理想化状态总利润差距表 本文通过分别变换ε、α分析参数变化对总利润的影响。ε是用在决策的一种策略, 如ε=0.9时,说明算法有90%情况会按照Q-table最优值选择行为,10%情况随机选取行为;α是学习率,能够决定某一次的误差有多少是需要被学习的。 3.2.1 贪婪度ε变化对利润的影响 在ε为0.9、0.7、0.5、0.3数值下分别实验,同时控制参数α不变。如图8所示,图中图例从上到下依次表示在参数ε=0.9、ε=0.7、ε=0.5和ε=0.3下总利润。可观察到每次实验有着总利润随着贪婪度增加而降低的趋势。 上述趋势的原因是Q学习在初始探索中,选用较高的贪婪值会使智能体对环境探索不全面,造成对更优策略的忽视,一定程度上导致相关阶段回报降低,进而致使总利润降低。因此,在初始探索时可以把ε的强度适当降低,这样更有利于算法的探索,从而有利于选择到合适策略。 3.2.2 学习率α变化对利润的影响 本文依次控制学习率α从0.1、0.4、0.7数值变化并保持ε不变来观察学习率对总利润影响。本文进行了多组实验,发现α的变化对总利润有较大的影响,α变化幅度越大,利润变化程度越大。 随机选取多次实验中的几组数据,对α=0.1、α=0.4、α=0.7情况下强化学习总利润求和,如图9所示。横坐标表示α的取值,纵坐标表示总利润,图例中的符号表示实验次数。可以发现,不同实验下,参数α从0.1到0.4再到0.7的总利润呈现递增趋势,这是因为随着学习率α的增加即学习效率增加,误差被学习的数量增加,导致获得的总利润提升。因此,当使用Q学习进行探索时,可以适当提高学习率α,以便获得更优的策略和回报。 为了优化框架协议下多周期报童产品库存决策问题,本文通过生成随机数来模拟不确定需求,并利用强化学习Q学习算法求解问题。把相应的订购期数作为状态s,订货的策略方法作为行动a,通过智能体Agent对当前状态的探索,来选取较优的订货方法和策略。有以下结论: 结论1强化学习Q学习算法进行订货决策能降低零售商订货成本、提高利润。 结论2通过对比研究Q学习算法和传统方法的总利润发现使用强化学习方法订货相比于传统订货方法(定量订货法、移动平均预测、指数平滑法)平均利润提高约7%~22%,且多次试验下强化学习决策相比理想状态的平均利润相差仅为8%左右,强化学习是一种有效的方法。 结论3本文通过对贪婪度和学习率这两个参数的研究,发现初始的贪婪度ε越高会影响算法的探索范围,并影响实验结果。为使探索范围更广策略更优,算法前期的贪婪度应适当降低。学习率α也会影响总利润,显而易见的是,随着学习率的增长,总利润也随之增长。 强化学习算法是建立在一定假设条件下进行的,会受到环境、算法训练次数等因素的影响。本文研究也存在不足之处,本文数据实验及实例部分较为简单,对训练数据长度及强度选取较小。另外,本文也只研究了常见的采购数量型框架协议。 未来可考虑带有更多约束条件的问题,如多地点预算约束、多周期多品种约束等;可以用强化学习进一步研究存在储存成本的多周期产品库存决策问题;在供应链方面,用强化学习方法考虑双方或多方博弈问题等都是值得进一步研究的方向。


1.4 模型分析

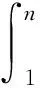
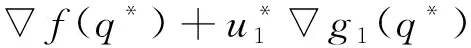



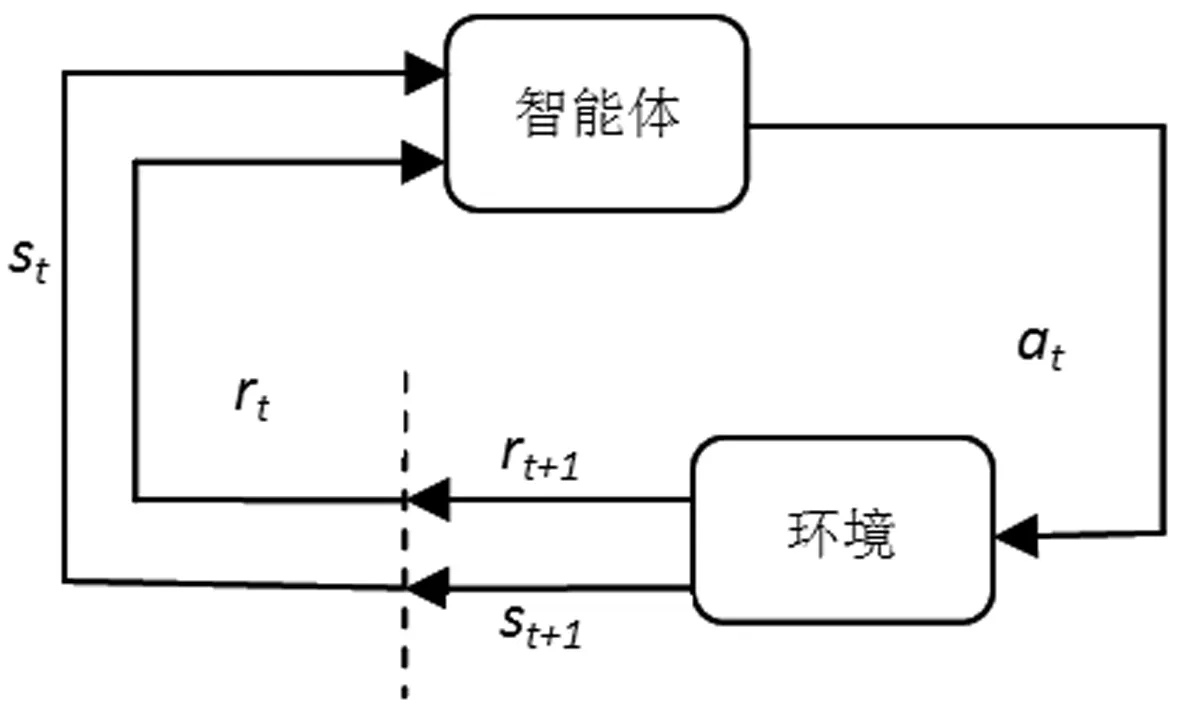
2 强化学习的库存决策模型

3 数值实验及分析

3.1 几种方法的总利润对比







3.2 参数变化对利润的影响
4 结论
