区块链技术影响下的供应链系统动态响应性研究

孙林辉, 葛晨晨,2, 吴安波, 袁晓芳

(1.西安科技大学 管理学院,陕西 西安 710054; 2.南京航空航天大学 经济与管理学院,江苏 南京 211106)

0 引言

牛鞭效应的控制与优化是多级库存管理研究与实践的关注焦点[1]。尤其针对“难储存、高风险、非标品”易腐品供应链和应急供应链。如鲜花供应链的分销商和零售商间供需信息不匹配时，导致高库存货损和巨大的资源浪费[2]。面对COVID-19，信息延迟将导致救治物资断裂，疫情防控困难[3]。如何通过有效信息技术提高企业信息的精准性、弱化牛鞭效应的负面影响等成为供应链管理中迫切需要解决的问题。近年来，企业中较多采用EDI、ERP和RFID等信息网络技术解决方案，然而由于技术架构的限制，数据交换受限于高昂的人工干预成本、低效的信息流同步、信息获取难度大且易被篡改，系统内部的信息无法与其他企业或部门整合等[4]，因而对牛鞭效应的控制作用并不显著。

区块链技术作为一种新兴的颠覆性信息技术正加速突破供应链管理领域的应用，为供应链中库存问题提供柔性的解决方案[5]。区块链技术能够解决需求不稳定导致的牛鞭效应[6]。相较于其他信息技术，区块链技术可与前沿技术相结合，简化信息集成的过程，提高信息实时共享的精准性、及时性和访问性[7，8]。在实际应用中Maersk和IBM成功应用区块链于全球物流供应链中，避免了因文档数据错误、信息不对称造成延误的机会，每年节约380亿美元的成本[9]。然而，区块链技术目前处于探索和研究初期，大部分中小企业对其如何应用并不清晰。因此本文基于区块链技术解决供应链系统中信息时滞和不准确的基础上，探究区块链技术的应用对于多级库存系统中牛鞭效应的影响，建立区块链技术影响下的供应链多级库存系统控制模型。

牛鞭效应的现象主要表现在订单信息和库存信息波动上。区块链技术保证需求信息准确性和及时性[10]，从而减少信息延迟时间[11]，降低库存水平的波动[12]，保证订单信息和库存的准确性[13]。牛鞭效应的控制与弱化的研究主要分为两大类：第一类通过数理统计方法量化牛鞭效应：刘红等建立三种需求预测技术对两级供应链牛鞭效应影响的量化模型及仿真模型[14]。代宏砚等建立解析模型量化分析在库存信息不准确的多级供应链系统中的牛鞭效应[15]；第二类通过控制论进行建模：Hoberg等人研究控制论中频率响应图、白噪声和度量供应链中牛鞭效应[16,17]。唐亮和靖可运用控制论中的鲁棒控制策略抑制不同形式客户需求引起的牛鞭效应[18]。

这些研究分别从静态和动态角度探讨牛鞭效应问题，已有的研究文献来看，(1)第一类方法通过详细的数理建模得到较为严谨的理论结果，但可能会对模型做过多的假设[19]。第二类方法虽模型设计较为复杂，但大量的研究表明控制论在处理系统的动态性能具有较强的优势；(2)国内外对牛鞭效应的成因研究集中在物流延迟[21]和交货延迟[20]，忽略了信息延迟对需求波动的影响，未能解释不通畅的信息结构和不同步的信息流造成的牛鞭效应问题；(3)尚未有文献通过定量方法研究区块链技术对牛鞭效应的影响。在此背景下，本文从动态角度出发，运用线性控制理论构建二级库存系统控制模型，引入区块链技术影响下的校正因子，设计二级库存系统控制模型的系统结构图，利用传递函数、时域响应分析、频域响应曲线和白噪声放大曲线分析比较顾客固定需求和随机需求信号输入下区块链技术对控制系统的动态响应特性。本研究量化区块链对供应链系统中牛鞭效应的影响，描述了不同需求下订单量和库存的动态响应，探究了区块链技术影响下的信息校正因子对牛鞭效应的抑制作用，丰富了区块链在供应链多级库存管理中的应用，揭示供应链背景下区块链技术应用的实际和理论意义，为易腐品供应链或应急供应链管理者提供新的技术思路。

1 多级库存系统控制模型

1.1 问题描述

本文在Hoberg的研究基础上采用级库存策略[17]。遵循Dejonckheere提出的基于控制论的分析三步骤：求导传递函数、绘制频率响应图、计算输出方差/输入方差(牛鞭效应量化值)[17]。考虑由一个分销商和零售商组成的二级供应链系统(如图1)，增加白噪声分析系统动态响应性。首先在每个周期T开始时，利用指数平滑法计算分销商和零售商的终端顾客需求；其次，通过供应链系统的提前期和安全放置时间计算其目标库存水平；然后，分销商和零售商依据库存偏差和顾客的需求预测值计算一个周期T末的订单量；零售商接收顾客的订单信息早于分销商，且零售商的需求满足后，再把其订单发送给分销商；最后，供应链上下游共享需求信息、库存信息和订单数据。具体假设如下：

(1)供应链中所共享的信息受到信息延迟的影响，包括数据输入异步过程中的延迟、信息传递的延迟，且各方的延迟时间为固定且已知；

(2)本文引入区块链技术影响下的信息校正因子，假设了区块链技术应用程度越高，需求预测信息越准确，需校正延迟和扭曲的信息越少，校正因子μ就越小，降低库存过剩，减少库存水平间的误差值。修正后的订单量可表示为Qt,n=Fn+μΔSn。其中Qt,n表示为订单量，Fn为预测值，ΔSn为库存误差。

(3)存在订单延迟时间，即当企业向上级供应商发出订单后，上级供应商通常会经过一定时间结束现在的生产任务后才会展开对新订单的生产任务；

(4)在运输和仓储过程中不存在货损现象；

(5)终端客户需求是随机的；

(6)用指数平滑模型表示需求函数；

(7)存在生产和物流延迟，即上级供应商收到订单后，需要一定生产时间和一定的运输时间。

符号设计如下：

αn：n级库存的指数平滑需求预测的因子;

Ln：n级库存的提前期;

Cn：n级库存放置时间以避免需求的不确定性;

Fn：一个周期T内的预测值;

TSn：一个周期T内的期望库存水平;

Sn：一个周期T内的实际库存水平;

ΔSn：一个周期T内的库存误差，ΔSn=TSn-Sn;

On：一个周期T内的订单量，Ot,n=Fn+ΔSn;

τ：信息延迟时间;

μ：区块链技术影响下的信息校正因子 ;

In：n级库存的库存水平。

1.2 库存系统建模

本文主要采用Z变换表示在频域中的库存系统，更精准的描述供应链中的运输延迟和信息延迟。因此延迟时间T的Z变换描述为z-T。其系统结构图如图1表示。

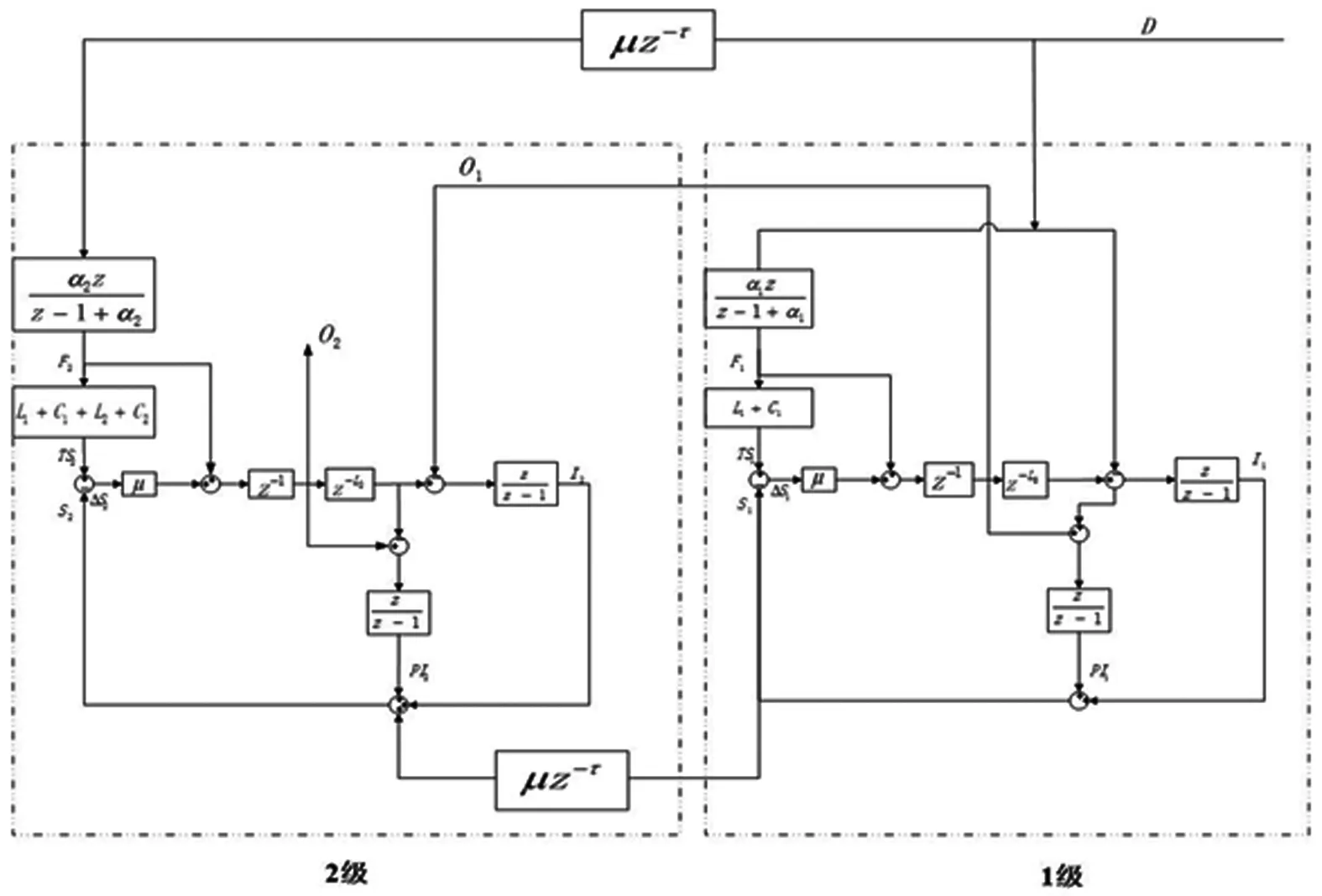
图1 区块链技术影响下的两级库存系统结构图

本文定义多级库存系统控制模型的输入量为随机的顾客需求，输出量为库存量和订单量，从而得到以下形式的传递函数。为简化公式的计算，令L1+C1=T1,L2+C2=T2。本文定义零售商的订单量O1(z)响应顾客需求D(z)，表示为GO1(z)=O1(z)/D(z)；零售商的库存量Ii(z)响应顾客的需求D(z)，表示为GI1(z)=I2(z)/D(z)。同分销商的传递函数分别表示为GO2(z)=O2(z)/D(z)和GI2(z)=I2(z)/D(z)。具体传递函数表示如下：

(1)

(2)

(3)

(4)

为确保库存系统的稳定性，本文利用Nise提出的极点法分析控制系统。零售商的订单量的传递函数GO1(z)，极点z1=1-α1，z2=1-μ，由于订单量的调整因子μ和指数平滑系数α均大于零且小于等于1，则z1和z2都在复平面的单位圆内，故系统稳定；零售商的库存量的传递函数GI1(z)，其极点z1=1-α1，z2=1-μ和z3=z4…zL+1=0，该系统稳定；分销商的订单量的传递函数GO2(z)，极点z1=1-α1，z2=z3=1-μ，z4=1-α2,z5=z6=…zτ=0。极点均在复平面的单位圆内，故系统稳定；分销商的库存量的传递函数GI2(z),其极点z1=1，z2=1-α2，z3=1-α2和z4=z5=1-μ,z6=z7…=zτ+L2-1=0，极点均在复平面的单位圆内，该系统稳定。

2 动态响应性分析

本节主要分别采用时域分析法、频域响应曲线和H∞-norm衡量供应链中的牛鞭效应，以此验证两级库存中引入的变量对多级库存中的信息延迟和牛鞭效应的抑制作用，从而证明此系统的有效性、合理性和创新性。

2.1 时域分析

线性控制系统中的时域分析通常在单位阶跃函数作用下，测定系统的动态性能。本节假定系统在单位阶跃输入信号作用下，分析供应链的订单量和库存量随着时间的响应。

(5)

其控制系统的脉冲传递函数为G(z)=C(z)/R(z)，而R(z)=z/(z-1)。则系统的输出量的z变换函数

(6)

为讨论参数μ对供应链系统中零售商订单量和库存量的时域响应过程。设定指数平滑系数α1=α2=0.2，供应链的提前期L1=L2=4和库存放置时间为C1=C2=1，利用MATLAB仿真得到其单位阶跃响应曲线。结果如图2～图4所示。

图2 零售商订单量的阶跃响应曲线

图3 τ=2分销商订单量的阶跃响应曲线

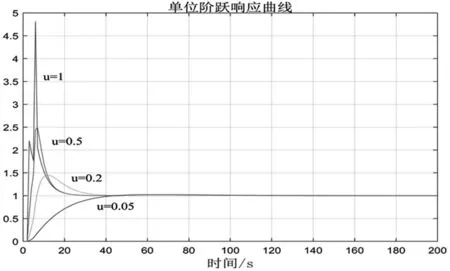
图4 τ=4分销商订单量的阶跃响应曲线

通过分析可得：(1)μ值越小，其订单量的阶跃响应越趋于平稳，最终趋于输入单位阶跃信号值1且系统的稳态误差为0；(2)对比图2和3，零售商的订单量峰值为2.2，而分销商受信息延迟的影响，订单量峰值为5.16。受信息延迟的影响，库存系统的订单量波动显著增大，在供应链系统易产生牛鞭效应；(3)μ值越小，系统的稳定性能越高，但其响应性反而降低；(4)对比图3和4，信息延迟时间越长，μ值抑制作用越显著，稳定性能越高，信息精准性越高。

2.2 频域分析

本节应用频率响应曲线衡量订单和库存波动效应。系统的频率响应是指一个样本周期内，在正弦波信号频率ω∈[0,π]输入时，系统输出输入的标准差放大率。

(7)

Re表示幅值的实部，Im表示幅值的虚部。

2.2.1 零售商的频率响应

为讨论参数μ对供应链系统中零售商的订单量和库存的放大效应影响。通过设定参数α1=α2=0.2，L1=L2=4和C1=C2=1，得到其频率响应图。结果如图5～图7所示，横坐标描述输入正弦信号(固定顾客需求)的频率ω，纵坐标为系统的输出，即订单量和库存量的放大量。

从图5和图6可观察到：当频率ω=0表示恒定需求，不论μ值的参数变化，订单和库存量均未波动。当频率ω趋于π时，订单量和库存量的放大频率振幅随μ值增大而减小。μ=1时，最大订单振幅为2.33和最大库存振幅1.58；μ=0.05时最小振幅分别为0.17和0.57。引入μ有效地抑制订单可变性和库存的波动。图7可知，库存量的波动伴随订单量的高可变性。

图5 零售商的订单量放大的频率响应曲线

图6 零售商的库存量放大的频率响应曲线

图7 零售商库存量和订单量放大频率响应曲线

2.2.2 分销商的频率响应

本节为讨论参数μ和信息延迟时间τ对分销商的订单量效应影响。同样设定相同的参数得到分销商的频率响应图。结果如图8和图9所示。

图8 τ=2时订单量放大频率响应图曲线

图9 不同τ值和μ值订单频率响应对比

(1)通过设定信息延迟时间τ=2时，从图8可知分销商的订单放大效应随μ减小而降低。此外，μ越小频率ω趋于π时，订单波动呈下降趋势且趋于0。

(2)当τ为随机，μ分别取0.2和0.5时，从图9可得：τ一定时，μ越小越能一直订单波动；μ一定时，τ越大其订单量波动越大。即，无论减少参数μ还是τ都能够有效抑制牛鞭效应，τ和μ都取到最小，ω趋于π时订单波动趋于0。

通过对零售商和分销商的频率响应分析，其库存量和订单量的波动均随μ值减小而得到有效的抑制。但是上述频域分析假设顾客的需求信号由单个正弦输入(固定需求)，属于理想状态下的顾客需求。需进一步，讨论随机需求输入时，参数μ对供应链多级库存系统的影响。

2.3 白噪声分析

本节利用白噪声放大来表示输入信号为随机的顾客需求。白噪声订单放大(H2-norm)主要描述正态分布需求下订单标准差与需求标准差之比。传递函数G(z)的稳定系统的H2-norm表述为‖G(z)‖2

(8)

为讨论随机顾客需求下参数μ和α对订单量的放大效应。通过设定参数L1=L2=4，C1=C2=1，依据上述计算步骤计算‖GO1‖2,利用MATLAB得到白噪声订单放大曲线(图7)。横坐标指数平滑系数，纵坐标为系统的输出。

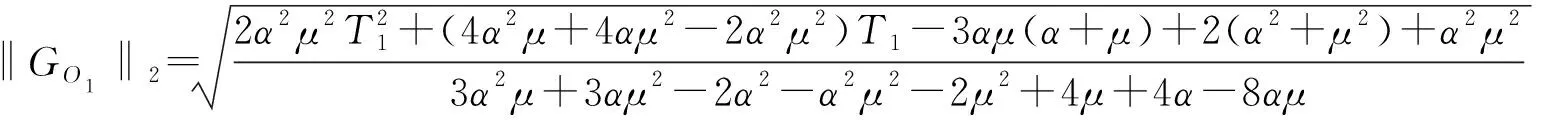
(9)

图10 零售商白噪声订单放大曲线

从图10可得当顾客需求为随机时，其订单可变性随着α和μ减小而降低。表明指数平滑系数和区块链技术影响下的信息校正因子均对订单波动有抑制作用。

图11 τ=2分销商白噪声订单放大曲线

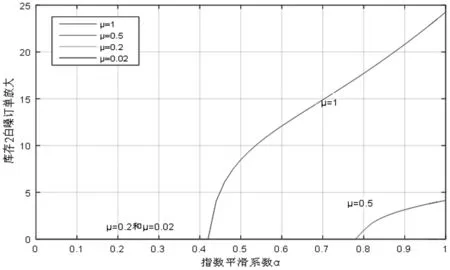
图12 τ=4分销商白噪声订单放大曲线

当参数，α1=α2=α时。得图11和12响应图。可得，即使受到不同信息延迟的影响，变量μ和α依然对订单波动具有显著的抑制作用。指数平滑系数α和区块链技术影响下的信息校正因子μ值越小，订单和库存的抑制作用越显著。

3 仿真数据分析与讨论

本节对上述系统进行计算机仿真分析，求取时域响应曲线上五项性能指标(表1)，对比固定需要和随机需求下零售商和分销商动态响应的幅值(表2～4)。

表1 多级库存控制系统的时域指标

表2 零售商频域响应和白噪声放大对比(α=0.2)

表3 分销商的动态响应数值

表4 分销商频域响应和白噪声放大对比(α=0.2)

由表1分析了多级库存系统在单位阶跃响应作用下的五项动态性能指标，表2～4描述控制系统在不同需求信号下的订单量和库存量频域响应曲线，通过对比分销商和零售商订单量时域指标和频域响应值，得出以下结论：

(1)引入区块链技术影响下的信息校正因子，降低了系统的响应性，但提高了库存系统的精准性和稳定性。通过分析不受信息延迟影响的零售商订单量，零售商的订单量响应的时间随着μ减小，呈逐渐递增趋势，响应时间从0.359s上升至4.029s，但订单量可变性显著被抑制。而对比受到信息延迟影响的分销商系统，同样存μ越小，系统稳定性和精准性越高，响应性越低问题。针对这一问题可解释：面对随机需求情境下，根据顾客需求下订单，未考虑实际的库存量或者市场销售需求，故库存的系统的响应性高，但系统存在过高的订单量，系统的超调量也会较大，势必引起上游企业库存量波动变大。区块链技术的应用有效促进信息的精准性、及时性和访问性，但随着区块链技术应用程度越高，处理复杂系统中的信息越多，导致系统响应时间增加，但也因此保证信息的精准性，缓解牛鞭效应。

(2)信息延迟时间愈长，区块链技术影响下的信息校正因子愈能有效抑制信息延迟所带来的牛鞭效应。通过对比τ=2和τ=4分销商的阶跃响应性能指标，其延迟时间、上升时间、峰值时间、调节时和超调量值总体相差较小。但当τ=4，μ=0.05时，系统的响应时间显著优于τ=2。通过对比超调量可见：信息延迟情境下，区块链技术的信息校正因子愈能有限抑制订单的可变性，增强系统的稳定性和准确性。当供应链系统中应用区块链技术时，信息延迟时间越长，越能达到弱化牛鞭效应的效果。

(3)随机需求信号下，α和区块链技术μ越小，订单量和库存量的抑制作用越显著，且系统的信息时滞越长，其抑制作用愈显著。尤其τ=4，α=0.2，μ=0.05时，订单量的频率放大的数值为0。对比表4所示，当信息时滞为2时，区块链技术对固定需求下订单可变性的抑制作用优于随机需求。而当τ>2时，区块链对随机需求下订单可变性的抑制作用优于固定需求。

(4)高库存可变性伴随高订单可变性

概言之，区块链技术应用供应链多级库存控制系统中，提高了系统的稳定性、准确性。解决供应链系统中信息时滞问题，并验证了区块链技术影响下的供应链库存系统的有效性、合理性。

4 结论

牛鞭效应导致了供应链效率低下和库存成本的积压，是企业供应链管理中亟待解决问题。本文为解决供应链系统中信息延迟和信息失真问题导致的牛鞭效应，应用区块链技术构建供应链系统控制模型，通过稳定性判定、时域分析法、频域响应图、白噪声放大探究区块链技术对信息延迟和扭曲下的供应链系统订单和库存的影响。系统仿真表明：信息延迟和扭曲会对供应链系统的绩效产生负面影响，而区块链技术的引入有效的抑制系统中订单可变性和库存的波动，提高库存系统的准确性和稳定性；与较短的延迟时间相比，信息时滞越长，区块链技术和指数平滑系数对牛鞭效应抑制作用越显著。

本文在前人研究的基础上，首次引入区块链技术构建多级库存系统控制模型，采用定量方法分析不同需求情景下区块链技术对系统订单量和库存量的影响，优化了库存控制系统的稳定性和精准性，量化了区块链技术对牛鞭效应的影响，丰富了区块链技术在动态供应链系统的研究。同时对于管理者的启示：(1)需求信息存在延迟现象时，应用区块链技术能够有效抑制库存系统的偏差，缓解牛鞭效应，以提高顾客服务水平；(2)面对需求信息不匹配且时滞较长时，管理者应尽可能减少指数平滑系数，系统中订单量可变性越小，库存系统越精准；(3)应用区块链技术时，系统响应时间会达到一个稳定阈值，这时系统性能的稳定性和准确性最优。本研究也存在一定的不足，未考虑区块链技术的应用成本，仅研究区块链技术对二级供应链控制系统牛鞭效应的影响。未来研究中，从博弈论角度探究区块链技术引入后，多级供应链系统动态变化和成本之间关系，达到供应链系统利益最大化。