面向任务保障的多组件系统效益优化策略

王 成, 许建新, 尚利俊

(1.西安航空学院 机械工程学院,陕西 西安 710077; 2.西北工业大学 机电学院,陕西 西安 710072; 3.佛山科学技术学院 经济管理学院,广东 佛山 528225)

0 引言

以任务需求和安全为导向的装备通常要求具备较高的可靠性，如执行飞行任务的飞机、执行运输任务的高铁以及执行作战任务的潜艇等，这些装备中的安全关键系统需要具备长时间稳定运行的特性。在安全关键系统组件构成结构确定的前提下，常采用冗余方法来提高系统的可靠性。合理的冗余设计将大大提高系统的可靠性，但同时也增加了系统的复杂度和设计难度，如何合理而有效的进行系统冗余设计是一个不断探索的课题。

近年来，学者们在冗余节点的优化设计方面取得了一些成果。宋征宇[1]提出了考虑成本效率的航天运输电子系统冗余设计方法，该方法既保证了系统的可靠性，又提高了成本效率。杜海东等[2]从产品设计角度出发，证明了在系统组成单元中对可靠度最低并且初始冗余数最少的部件增加冗余设计可以有效提高系统总体可靠性水平。赵敏等[3]为了提高监测系统的可靠性，将备件部署在风电机组中极易发生故障的部件上，并根据建立的目标函数确定最优的备件数目。诸震亚等[4]采用点失效模型可靠性方法来实现备份节点的优化部署，在原网络基础上通过增加备份节点的方式来提高网络的可靠性。李亘等[5]为了整体提升全自动无人驾驶地铁车辆的安全性和可靠性，充分考虑各组成系统的冗余设计及优化方法。LEVITIN等[6]提出了一种用于平衡任务成功概率和系统损失风险的冗余分配方法。综述上述，现有研究大多以成本控制或可靠度为优化目标，很少有从运行效益的角度对整个系统进行优化的研究，因此如何保证系统在执行任务期间可靠运行的前提下实现效益最优将是本文研究的重点。

近年来，随着重要度(Importance Measures, IM)理论的不断发展，采用IM驱动的通用框架来解决复杂系统可靠性优化问题已成为一种有效的手段[7]。目前研究比较活跃的IM方法有Birnbaum重要度(Birnbaum Importance, BI)[8]、关键重要度[9]、综合重要度[10]、网络重要度[11]等，有关IM的最新进展请参阅相关文献[12,13]。鉴于重要度在复杂系统应用方面的优势，本文从系统效益的角度出发，构建了系统可靠性模型，定义了效益重要度(Yield Importance, YI)，提出了一种面向任务保障的多组件系统效益优化策略。当系统可靠度下降到设定阈值时，计算系统各组件的效益重要度，选择效益重要度最大的组件进行备件分配，如此进行迭代，直到完成任务要求，最终形成最优的备件分配序列。

1 问题描述

假设系统由一系列不同的组件串并联组成，系统的可靠度由这些组件的可靠度来衡量。在一次任务保障中，系统可靠度要长期保持不低于最小可靠度阈值，需要对现有组件增加适量的备件，在系统整体可靠度低于设定阈值时切换到备件用于提升系统可靠度。考虑到空间和效益问题，不可能给每个组件配置过多的备件。因此，当系统可靠度低于设定阈值时，选择效益最高的组件进行一次备件切换工作，以此类推，直到完成任务。系统可靠度随时间和备件切换而发生的变化规律示意图如图1所示，注意到由于每次仅选择效益最高的组件进行备件切换，因此系统在运行期间的整体可靠度常常小于1。

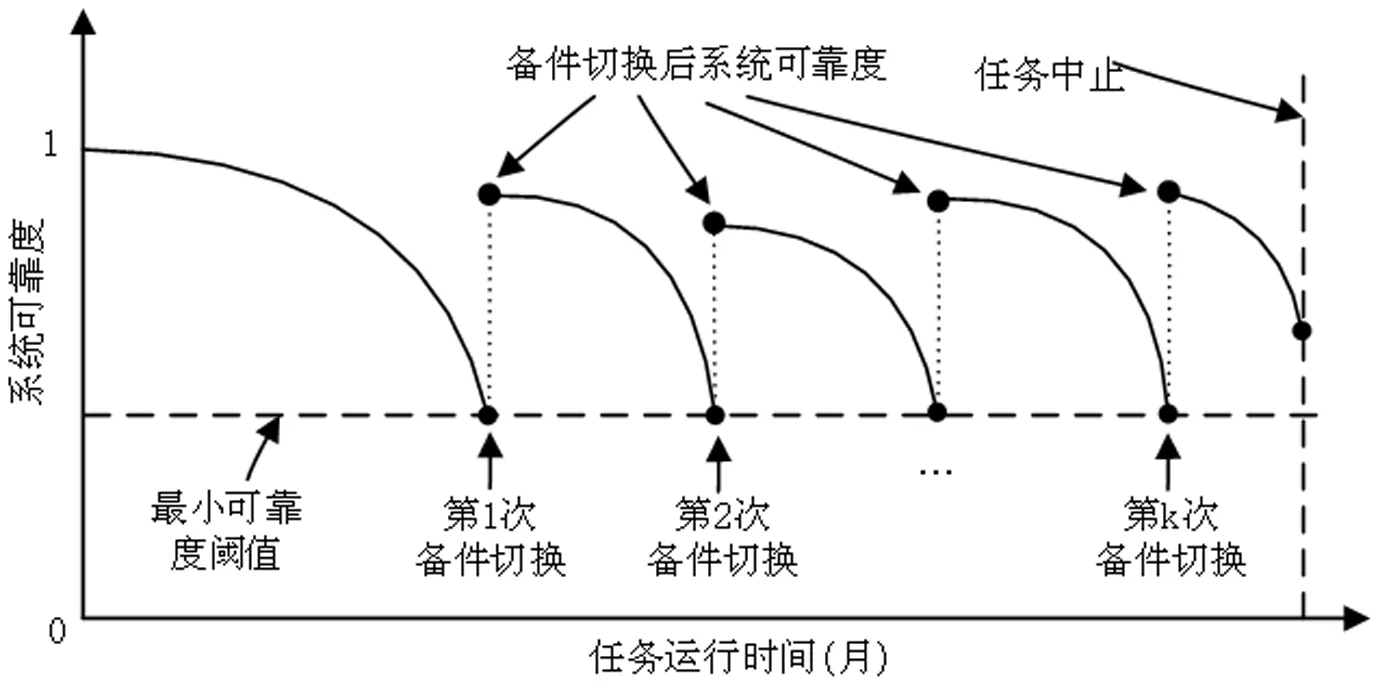
图1 系统可靠度随时间和备件切换变化规律示意图

本文所要解决的问题是在系统正式投入使用之前，制定一个面向任务保障的系统最优效益备件分配序列。为了保证研究的有效性，特作如下假设：

(1)每个组件之间相互独立；

(2)性能退化是唯一引起失效的原因，即不考虑外界环境对组件的影响，如人为破坏，自然灾害等；

(3)每个组件都是全新的，即初始退化量θi=0；

(4)备件在休眠期间性能不退化；

(5)不考虑因系统可靠性降低带来的风险成本。

2 系统可靠性建模

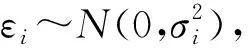
对于每个组件而言，当其性能退化水平Xi达到其失效阈值Li时，则认为该组件失效。失效阈值集合由L表示且L={L1,L2,…,Ln}。每个组件的失效阈值根据自身特性进行预设。因此每个组件的可靠度Ri(t)表示为Xi不超过Li的概率，即

(1)

式中：Φ(·)表示标准正态累积分布函数。

假设系统由m个子系统组成，每个子系统包含ni个组件，整个系统的可靠度R(t)可以表示为

(2)

式中：m表示子系统的数量；ni表示每个子系统包含组件的数量，且i∈{1,2,…,m}；Rij(t)表示第i个子系统的第j个组件的可靠度。

3 系统效益优化策略

3.1 目标函数

将系统可靠度下限阈值和任务保障时间作为约束条件，以系统收益作为目标函数，建立系统收益优化模型为

f=max(ZS),s.t.R(t)≤σ,t≤S

(3)

式中：ZS表示目标函数，其由周期内运营带来的收入(V)与运营成本和备件成本之和(C)之间的差异组成，即ZS=V-C；σ表示系统可靠度下限阈值；S表示系统运行总周期。

对ZS进一步展开为

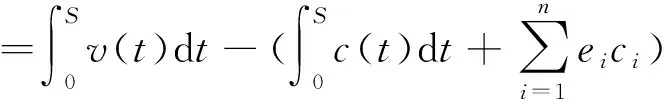
(4)

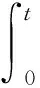
3.2 效益重要度

备件分配序列属于非线性整数规划问题，使用一般的规划论方法求解过程较为复杂，本文借鉴了边际效应思想进行优化求解，以达到对有效资源的合理分配。为此，将系统收益最大化问题转化为在任意一次切换时刻选择哪一个组件进行备件切换才能使当前时刻的系统净收益最大。为了能够量化表示在任意一次切换时刻系统的净收益，构建了效益重要度，具体构建过程如下。

(1)系统净收益形式化

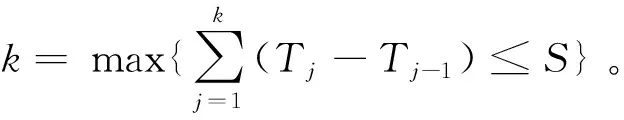
设y(t)为第i个组件进行备件切换前且不考虑其自身成本的系统收益函数，其表达式为

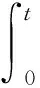
(5)

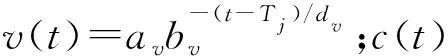
由式(5)可知，第i个组件进行备件切换前且不考虑其自身成本的系统期望收益E(y(t))可以表示为

(6)

式中：F(t)表示第i个组件进行备件切换前系统的寿命分布函数；R(t)表示第i个组件进行备件切换前系统的可靠度函数。

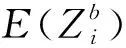
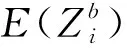
(7)

同理可知，对第i组件进行备件切换后且不考虑其自身成本的系统期望收益E(yi(t))可以表示为

(8)

式中：Rω(t)表示第i个组件进行备件切换后系统的可靠度函数；Fω(t)表示第i个组件进行备件切换后系统的寿命分布函数。

为了量化描述Rω(t)，首先要开展第i个组件备件的切换行为对第i个组件可靠度的影响研究。假设第i个组件工作一段时间后对其进行备件切换，此时的组件可靠度相当于通过一个时间的正向偏移量来提升其可靠度直到为1，即

(9)

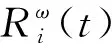
由式(9)可知，第i个组件备件切换后对整个系统的可靠度会有一个提升量，此时的系统可靠度函数可以表示为Rω(t)，且Rω(t)=R(t-ε),0<ε<τ，其中ε表示由第i个组件备件切换时对整个系统可靠度提升所需的时间正向偏移量。

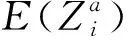
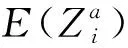
(10)

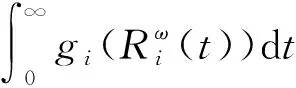
由式(7)和式(10)可知，经过第i个组件进行备件切换后，整个系统的期望净收益E(Zi)可以表示为

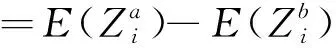
(11)

为了使R(t)能够由含Ri(t)的表达式来表示，本文采用枢轴分解定理[7]和BI理论[8]对R(t)进行变形展开，具体过程如下：

由枢轴分解定理可知，R(t)可以表示为

R(t)=Ri(t)R(1i,t)+(1-Ri(t))R(0i,t)

(12)

式中：Ri(t)表示第i个组件的可靠度；R(1i,t)表示当第i个组件正常时在t时刻的系统可靠度；R(0i,t)表示当第i个组件失效时在t时刻的系统可靠度。

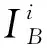
(13)

根据式(12)和式(13)可知，R(t)可以变形为

(14)

同理可知，Rω(t)可以变形为

(15)

将式(14)和式(15)代入式(11)可得

(16)

(2)效益重要度定义

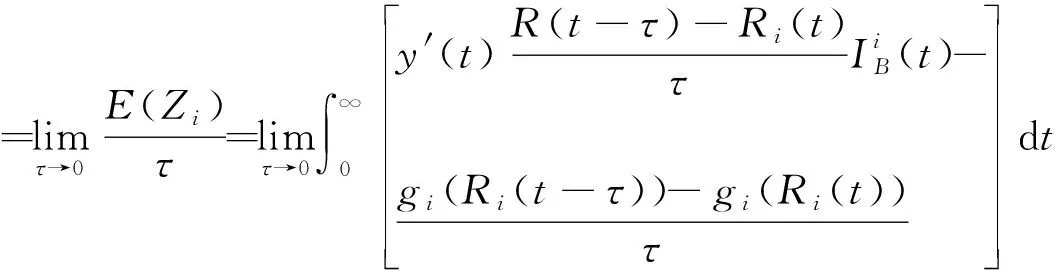
(17)

(18)

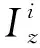
(19)

3.3 基于效益重要度的备件分配

在系统可靠度阈值以及运行时间两个约束条件下，采用模拟消耗式备件的方式来反向求解各组件备件的分配序列。当系统可靠度低于设定的阈值时，将待切换的各组件的效益重要度从大到小依次排列，对效益重要度最大的组件进行备件切换，假设切换过程没有时间延迟，切换完成后系统继续运行，并根据约束条件决策是否进入下一次切换。最后，求出整个运行周期内各切换时刻对应的备件，形成含切换时刻的备件序列。详细的分配过程如图2所示，具体步骤如下：

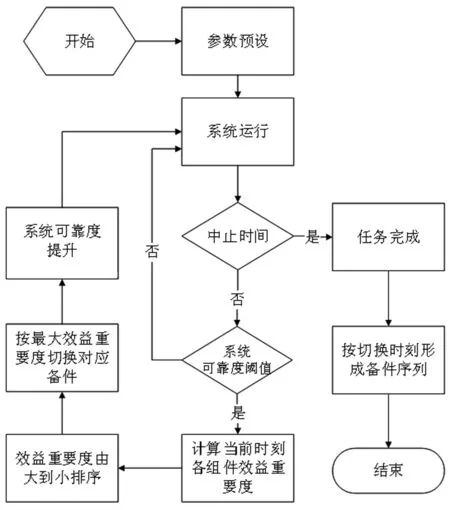
图2 备件分配过程

步骤1参数预设。按照任务保障的要求，设置系统可靠度下限阈值以及运行时间。

步骤2系统运行。判断系统运行时间是否到达任务中止时间，如果到达，任务完成。如未到达，判断系统可靠度是否下降到预设阈值，如果高于预设阈值，系统继续运行；如果低于预设阈值，进行步骤3。

步骤3组件备件切换。当系统可靠度下降到下限阈值时，计算各组件效益重要度，按照效益重要度由大到小排序，按最大效益重要度无时差地切换对应备件，其形式化表示为

⋮

⋮

(20)

式中：cSj表示第j次组件切换时选择的备件；fj(·)表示第j次组件切换时的映射函数。

切换完成后，转到步骤2继续运行，同时记录当前切换时刻的组件备件。

步骤4组件备件序列求解。当任务完成后，对每次切换的组件备件进行序列统计，形成含切换时刻的备件序列。由式(20)可知，在整个系统运行总周期内的组件备件序列可以表示为{cS1,cS2,…,cSj,…,cSk}。

4 数值仿真验证

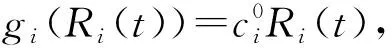
图3 由4个组件组成的串并联系统

(21)

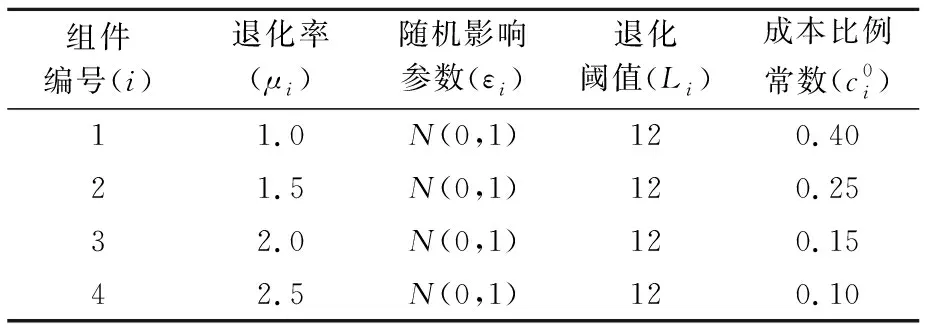
表1 组件规格参数

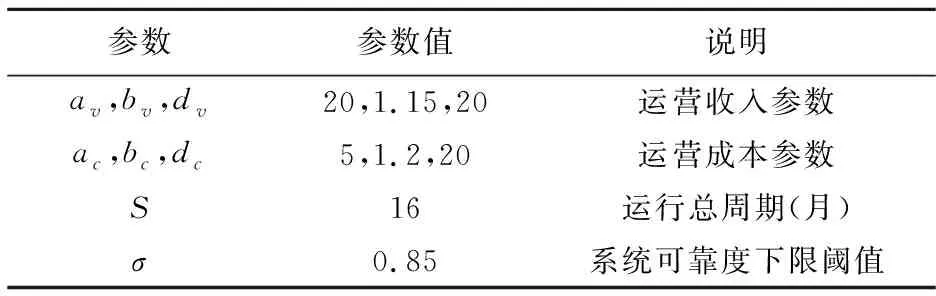
表2 系统运行参数

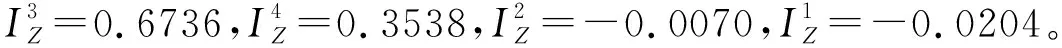
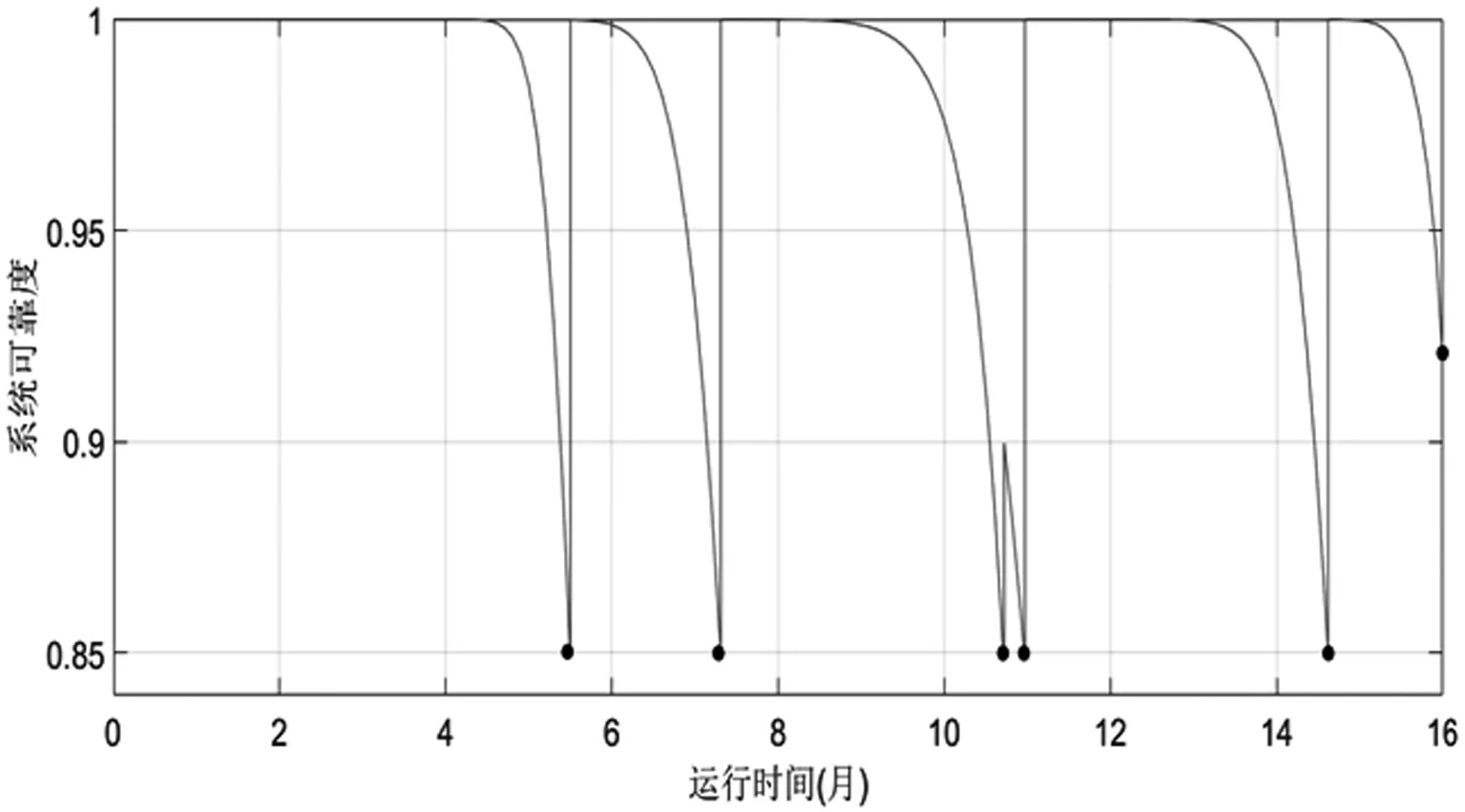
图4 系统可靠度随时间变化规律

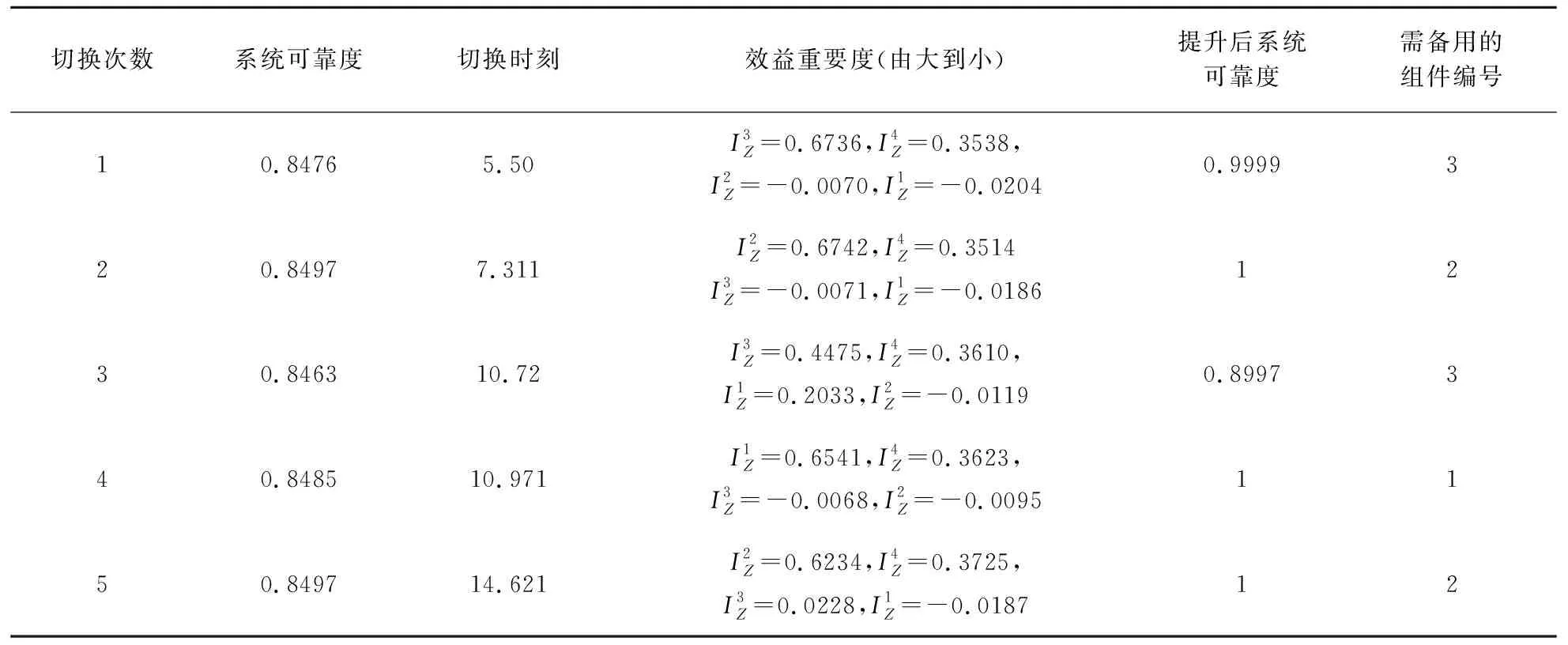
表3 系统备件分配明细

5 结束语

安全关键系统的长期稳定运行是按期完成任务保障的基础，从系统效益的角度出发，提出了一种面向 任务保障的多组件系统效益优化策略。该策略采用基于效益重要度的分配原则来确定备件数量，不仅使整个系统的可靠性得到了提升，同时也使备件达到效益最大化。数值仿真结果直观明了且符合预期。在后续研究中可以考虑更加复杂的连接结构以及增加组件之间的依赖关系。