正交法/响应面法四点接触桃形沟球轴承参数优化*
2022-11-10高福生贾瑞超姜淑凤闫朝竣王俊峰
高福生 贾瑞超 姜淑凤③ 闫朝竣 王俊峰
(①齐齐哈尔大学机电工程学院,黑龙江 齐齐哈尔 161001;②齐重数控装备股份有限公司,黑龙江 齐齐哈尔 161005;③黑龙江省智能制造装备产业化协同创新中心,黑龙江 齐齐哈尔 161001)
四点接触球轴承属于分离型轴承的一种,可以承受径向载荷和轴向载荷,使其承载性较高,常应用于风力发电、重型机床、精密仪器以及军工领域等[1-2]。这类零部件在使用过程中,其几何参数决定了承载性能与使用寿命,而加工这类零件的过程中其几何参数也决定了加工精度。因此,研究如何提升四点接触球轴承的几何参数优化,提升轴承使用寿命有着非常重要意义。
国内外学者对四点接触球轴承进行了大量的研究。例如,Rivera G 等人[3]等人、Joshi A 等人[4]和Chen L 等人[5]研究了四点接触轴承的运转矩阵、摩擦力矩控制方法及刚度分析;何培瑜等人[6]分析了球直径对轴承性能的影响;陈月等人[7]研究了四点接触球轴承内圈和外圈圆度误差对轴承旋转进度的影响;伍黎等人[8]采用有限元软件模拟了四点接触球轴承的接触特性和载荷分布规律;张占立等人[9]分析了四点接触转盘球轴承的负游隙与摩擦力矩的关系。以上各种研究中主要集中在对四点接触球轴承几何参数的复杂关系,对于四点接触球轴承寿命的提升研究较少。
为了研究如何提升四点接触球轴承寿命,本文以轴承寿命为目标函数,以滚子数量、滚子直径、垫片角和轴承游隙为影响因素,基于正交试验法和响应面法对其进行优化设计。
1 轴承优化数学模型的建立
四点接触球轴承的内、外圈沟道截面图呈现桃型,被称为“桃形沟”,当轴承不受载荷作用时,轴承中的钢球和“桃形沟”只有四点接触,进而被称为四点接触桃形沟轴承。四点接触球轴承结构如图1 所示。

图1 四点接触球轴承结构示意图
图1 中Dw为滚子直径、α为垫片角、Z为轴承滚子和Gr为轴承游隙。这是四点接触桃形沟类轴承的主要几何参数,影响加工精度与使用寿命。
1.1 四点接触球轴承寿命计算方法
研究球轴承寿命的决定因素时将基本额定寿命作为目标函数,如式(1)所示,L为基本额定寿命。

将式(1)转化为以时间为单位的Lh表示。
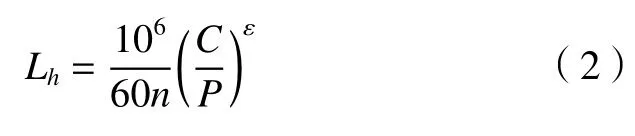
式中:C为轴承径向基本额定动载荷;P为轴承径向当量动载荷;ε为轴承寿命指数,原始设计中取值四点接触球轴承中ε=3;n为轴承转速。
当四点接触球轴承滚子直径Dw的取值小于25.44 mm 时,径向基本额定动载荷C的计算公式为

式中:bm为常用优质淬火轴承刚和良好加工方法额定系数;fc为轴承零件几何形状、制造精度及材料有关的系数;i为滚动体列数;α为公称接触角;Z为滚子数;轴承径向当量动载荷P计算公式为

式中:X为径向动载荷系数;Y为轴向动载荷系数;Fr为径向载荷;Fa为轴向载荷。
经式(3)与式(4)代入推导后式(2)变为基本额定寿命时间计算式(5)。
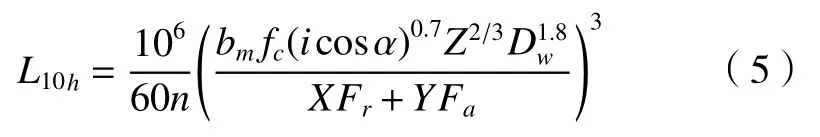
1.2 约束条件
根据式(5)可知,影响四点接触轴承寿命的因素主要有轴承的滚子数量Z、轴承滚子直径Dw、垫片角和轴承游隙Gr。四点接触球轴承在实际工程应用中为保证其强度,相邻滚子间距需大于0.15Dw,即约束条件的计算条件为

式中:DPW为球组节圆直径;Cmin为相邻滚子间的周向间隙。根据参数经过转化其约束的条件范围如表1 所示。

表1 轴承设计变量约束条件
根据上述约束条件,以原始设计的四点接触球轴承的车床加工过程为模拟原型,设定其内圈转速15 000 r/min,参考其他学者的研究成果取值Fr为3 500 N,滚子数量为21 个,其他主要参数如表2所示。

表2 四点接触球轴承主要结构参数 mm
通过查表得到:bm=1.3,fc=189.2,X=0.66,Y=1代入公式(6),通过计算该四点接触轴承寿命为7 119 h。为进一步验证四点接触球轴承寿命与轴承滚子数量、滚子直径、垫片角和轴承游隙之间的关系,以轴承滚子数量、滚子直径、垫片角及轴承游隙间距为影响因素,以轴承寿命为优化目标对该四点接触球轴承进行优化设计。
2 轴承优化设计
2.1 正交试验法轴承优化设计
轴承的滚子数Z、滚子直径Dw、垫片角α以及轴承游隙Gr是影响着轴承的寿命的主要参数,为确保试验结果的优化,采用正交试验法,是一种研究多因素的设计方法,从全部试验中挑选出具有代表性的因素进行组合[10-12]。本研究将轴承滚子数Z、滚子直径Dw、垫片角α及轴承游隙Gr作为正交试验法的影响因素,首先构建正交试验表如表3 所示。

表3 轴承优化设计变量(正交实验因素水平)
正交试验4 因素5 水平则表示为L25(54),如不采用正交法经计算需进行625 次试验,而采用正交实验法只需进行25 次,通过分析确定最优设计方案,25 种正交试验组合方案及计算结果如表4所示。
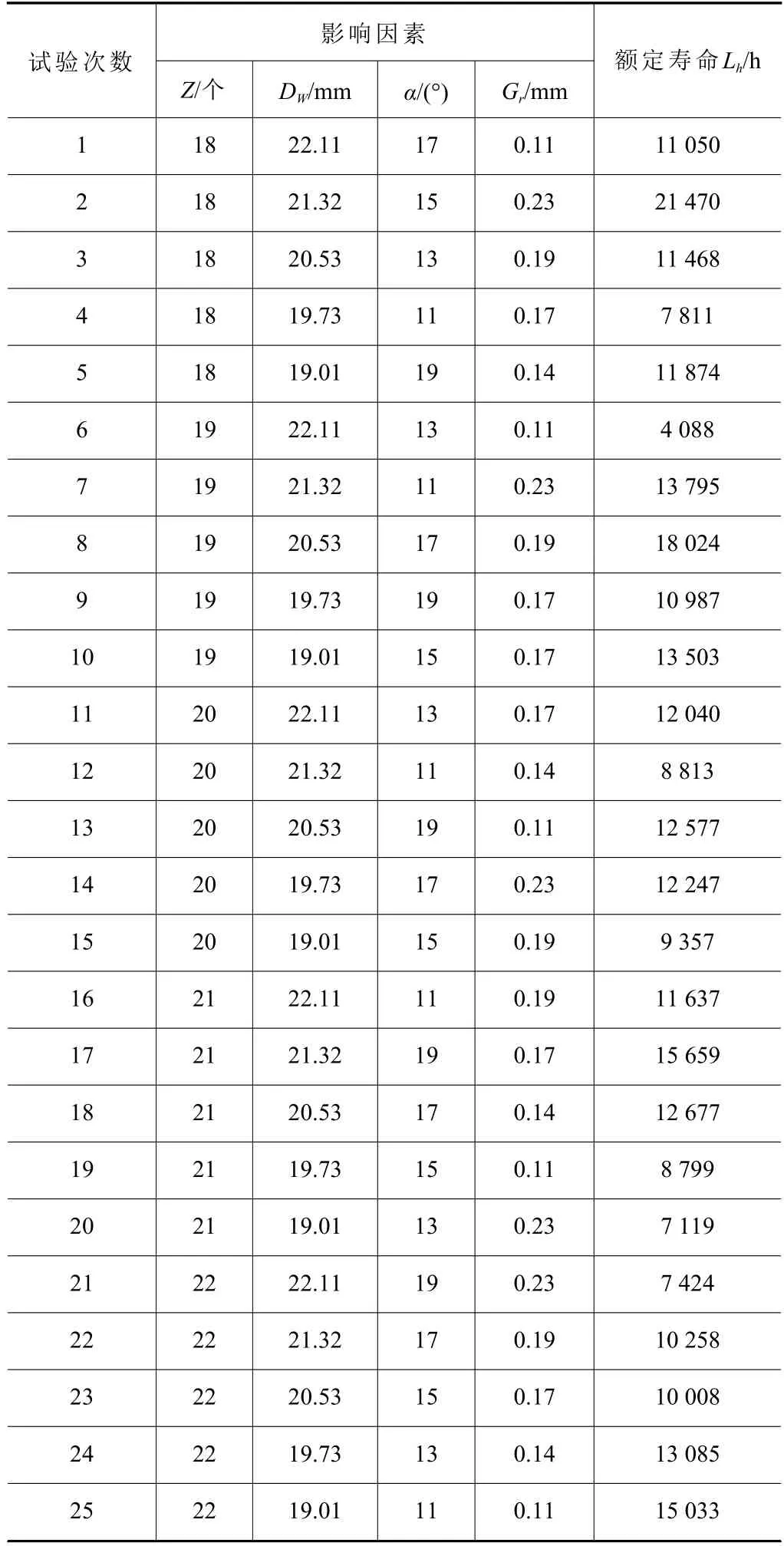
表4 轴承优化设计正交试验计算结果统计表
对表4 的统计数据分析可知,不同影响因素对于轴承寿命的影响所呈现的规律是不同的,还需要其他方法辅助进行分析最终确定轴承的参数优化方案。
2.2 基于响应面法优化方案的确定
响应面法是采用有限的试验次数,通过回归拟合的表达式代替实际功能函数曲面。标准响应面函数的表达式为[13-15]
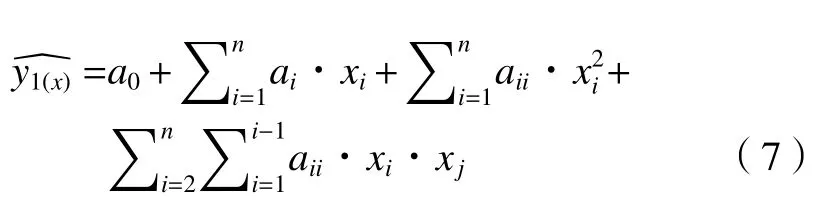
式中:xi为设计变量;n为设计变量的个数;a0、ai、aii和aij均为多项式待定的系数。
响应面合理性的评估通常由决定系数(R2),均方根函数(RMSE)以及相对最大绝对误差(RMAE)所决定[13-15],其计算公式分别为

为了更加直观地判断出响应面拟合的合理性,可以通过查看其计算值与模型预测值的关系图进行判断,越接近预测线代表其计算结果越准确。
将正交试验25 次组合方案中除去第20 次即优化前轴承组合方案外,另外24 次试验方案所得出轴承寿命填入到Design-Expert 软件响应面法模块中,首先确定正交试验组合方案计算的轴承寿命与模型预测值的情况,对比结果如图2 所示,其中,离散点为试验得出轴承寿命,直线为模型预测值。
通过对图2 分析可知,正交试验计算出的轴承寿命与模型预测出的轴承寿命较为接近。当需要获得精确参数时候需要对模型系数显著性进行检验,结果如表5 所示。
通过X的取值经过式(8)~(10)计算得出,决定系数R2为0.990 5,均方根函数RMSE为0.983 2,相对最大绝对误差RMAE为0.963 2,并通过分析表5 中数据可知,P<0.005 代表有显著性差异,P<0.000 1 代表具有极显著差异,该设计模型有意义。因此,说明正交试验法计算出的轴承寿命结果较为合理,具体最优方案的选值要根据各因素的影响规律分析进行确定。

表5 轴承优化设计变量
2.3 各因素影响规律分析及最优参数的确定
各因素影响轴承寿命值的大小可通过表5 中载荷F值的大小及等高线图进行判断。F值越大影响因素越大,等高线越接近椭圆形,表明两个因素间的交互作用对轴承寿命的影响越显著[16-17],各因素间的等高曲线如图3 所示,其中变量的单位如表3所示。
通过对图3 等高线的分析,根据F值的大小,可以得出随着滚子数和滚子直径的增大轴承的使用寿命值增大;随着垫片角度不断地增加,轴承寿命先增大后减小再增大;随着轴承游隙不断增大,轴承寿命先增大再趋于平稳。因此,各因素对轴承寿命的影响大小顺序则为:垫片角>滚子直径>滚子个数>轴承游隙。
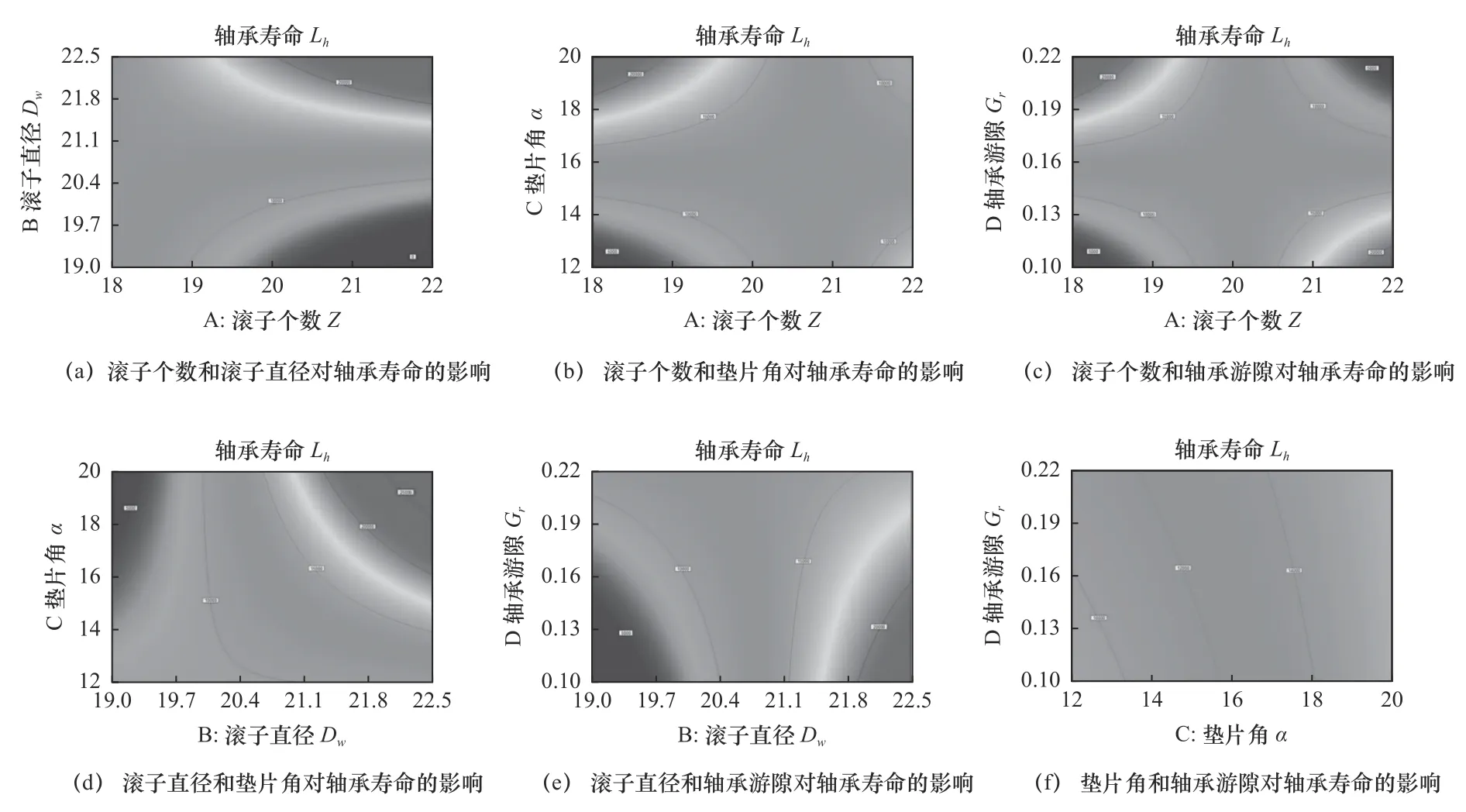
图3 各因素对轴承寿命影响的等高线
通过Design-Expert 软件的优化模块得出轴承优化的最佳组合方案为滚子数19 个,即轴承最优化方案为正交试验的第9 次试验方案。
2.4 优化设计的结果对比
通过以上分析可知,四点接触球轴承最佳设计方案为正交试验第9 次组合方案,其滚子个数为19,滚子直径为19.73 mm,垫片角为19°,轴承游隙为0.17 mm,轴承使用寿命为10 987 h。优化后轴承参数与优化前轴承参数对比结果如表6 所示。
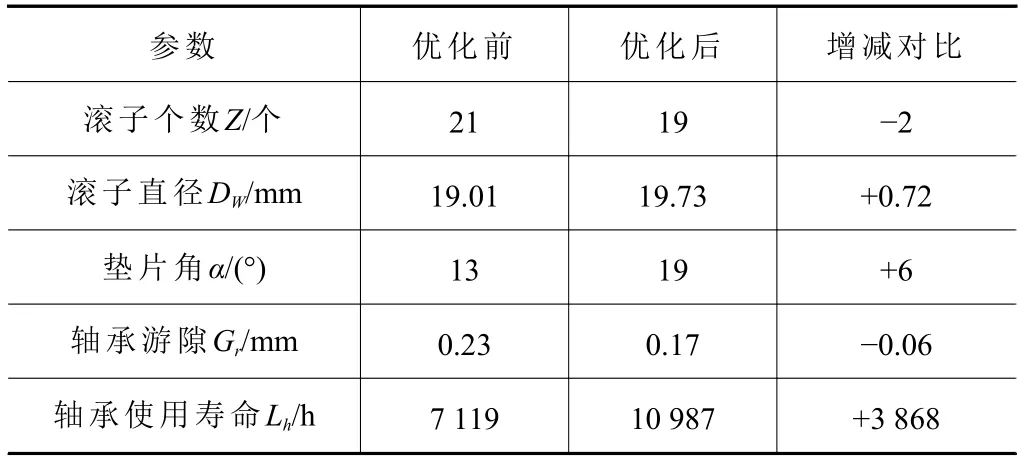
表6 轴承优化前后对比
由表6 的数据分析可知,优化后四点接触球轴承滚子个数减少2 个,轴承游隙减少0.06 mm,滚子直径增加0.72 mm 及垫片角增加6°后,优化后的四点接触球轴承寿命比优化前四点接触球轴承寿命增加了3 868 h,轴承的寿命得到明显提升。
3 横向实验数据对比分析
由于轴承在使用过程中的耗损受实际工况的突发因素影响不可预控,因此模拟实验获得的采样数据是参数优化设计的有效参考值,本课题的模拟实验结果证明了对轴承疲劳寿命影响最大的因素是滚珠直径,为了证明理论分析的正确性,通过横向比对相关研究[18]给出的最优的滚珠直径的尺寸与寿命提高比例关系,相关实验数据对比结果如表7 所示。
根据分析表7 实验数据可知,在使用寿命提高比例接近的情况下,滚珠数量减少时滚珠直径增加,有利于转速与荷载增加,本课题的模拟实验结论有效。
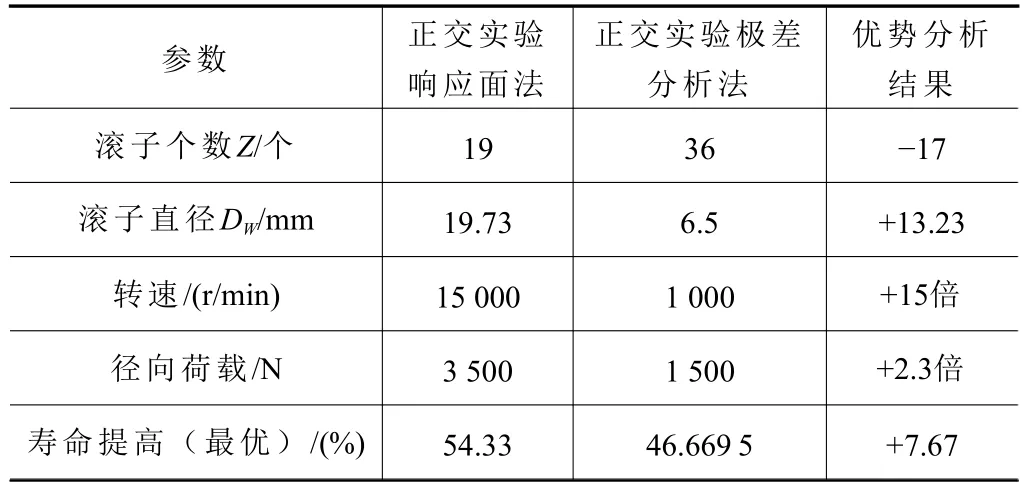
表7 轴承优化横向模拟实验数据对比
4 结语
基于正交实验法和响应面法对四点接触桃形沟球轴承进行参数优化设计,得到如下结论:
(1)滚子个数、滚子直径、垫片角和轴承游隙是轴承寿命的直接影响因素,随着滚子数、滚子直径的增加轴承寿命增加;随垫片角增加,轴承寿命先增加后减少再增加;随轴承游隙的增加,轴承寿命先增加后趋于平稳。顺序为垫片角>滚子直径>滚子个数>轴承游隙。
(2)滚子个数为19,滚子直径为19.73 mm,垫片角为19°,轴承游隙为0.17 mm 为基于原始设计的四点接触球轴承最佳优化设计方案,优化后四点接触球轴承寿命比优化前四点接触球轴承寿命增加了54.33%,优化效果明显。
上述结论证明了优化方案的可行性,验证了滚子个数、滚子直径、垫片角和轴承游隙对轴承寿命的影响规律,为轴承优化设计提升新思路。
