基于两种建模方法的冗余并联机器人的动力学对比研究＊

郝亮亮 刘小娟 杜 婷 闫献国

（①太原科技大学能源与材料工程学院，山西 晋城 048011；②山西科技学院，山西 晋城 048011）

并联机器人经过近30 年的发展和国内外学者的研究，因其具有输出精度高、刚度大和承载能力强和整体结构紧凑等优势[1]，已广泛应用于康复医疗[2]、飞机装配[3]、分拣包装搬运[4-5]和打磨机构[6]等。其中冗余并联机器人是具有更大的承载能力、更高的刚度和更高的定位精度且可输入构件数多于机构输出自由度的并联机构[7]，因此受到了研究者的广泛关注，成为国内外机器人和机构学领域的研究热点[7-10]。

2-UPR/2-RPU 并联机器人是五轴混联磨床试验机的核心机构，需要系统输出按照期望位姿及轨迹路线稳定前行，在工作过程中受到动态载荷的影响使其控制难度增加，因此为了改善机构的力学性能，运动学及动力学模型是并联机构特性分析的基础。研究人员常用的动力学建模方法有包括牛顿-欧拉法[1]、拉格朗日法[7]、凯恩方程法[10]和虚功原理法[11]等。其中拉格朗日法以其方程表达清晰且结构紧凑，无理想约束力的优点成为冗余并联机器人最常使用的方法；而虚功原理则是以机构为整体，用广义坐标消除约束力和关节惯量，因此其方程形式简单[12]。

但是由于冗余并联机构结构复杂、构件数量较多，因此采用传统的方法求解其动力学方程极为复杂，而引入螺旋理论结合传统动力学方法建立的动力学方程适用于复杂机构的运动学和动力学的研究，目前已经应用于复杂并联机构的研究中。韩博等[13]应用螺旋理论求解了机构的速度及雅可比矩阵，推导了各杆件的角加速度与质心线加速度，运用牛顿-欧拉方程和虚功原理方法相对四面体3RR-3RRR 可展机构的动力学进行了分析仿真，结果表明此方法分析过程简单且易编程计算。张荣敏等[14]采用旋量理论下的牛顿-欧拉方程构建了2 自由度解耦球面并联机器人的动力学方程。陈原等[15]以复合式移动机器人球面并联腿机构为研究对象，运用影响系数法推导速度和加速度影响系数矩阵，采用拉格朗日方法建立了球面并联腿机构的动力学模型，并应用数值仿真法验证了模型的正确性。柴馨雪等[16]采用螺旋理论结合虚功原理对2-UPR-RPU 并联机器人复杂运动状态下的动力学特性并进行了分析。李二伟等[17]基于螺旋理论建立了大型重载并联稳定接货平台的动力学解析模型。高名旺等[18]用螺旋理论推导了4-RRR 冗余并联机构的雅可比矩阵，采用牛顿-欧拉法计算主元点的惯性力螺旋，运用虚功原理构建了机构的动力学公式。林光春等[19]针对新型2-UPR/2-RPU 结构冗余并联机构采用虚功原理成功构建了该机构的动力学模型，结合驱动力二范数的最优方法对机构的驱动力和驱动功率方程进行了推导。

为验证两种动力学建模的正确性，采用螺旋理论和拉格朗日法建立并联机器人的动力学模型；在MATLAB 中编程得到并联机构的算法，求解得到动力学模型各支链驱动力数值仿真结果，并通过与ADAMS软件的动力学仿真结果进行仿真验证和误差分析。

1 冗余并联机器人运动学建模

2-UPR/2-RPU 并联机器人的机构简图和虚拟样机图如图1 所示，其由固定在机床上的定平台、包含冗余移动副驱动的2 条UPR 支链和2 条RPU 支链以及末端执行的动平台3 部分组成，整个机构呈对称分布。其中Mi(i=1,2)为动平台上R 副的中点且与支链UPR 的R 副中点重合，Mi(i=3,4)为支链RPU 与动平台相连的U 铰中心点，Si(i=1,2)为支链UPR 与定平台相接连的U 铰中心点，Si(i=3,4)为分支支链RPU 与动平台相连的R 副中心点。

图1 并联机器人机构简图和虚拟样机图

在定平台几何中心处建立O-XYZ全局坐标系和位于动平台处的动坐标系o-xyz，边长分别为a和b的正方形M1M2M3M4、S1S2S3S4，该冗余驱动并联机器人的自由度[20]为2R1T，共有3 个自由度。在全局坐标系下点Mi(i=1,2,3,4)的矢量坐标分别为

点Si（i=1,2,3,4）在动坐标系下的坐标矢量为

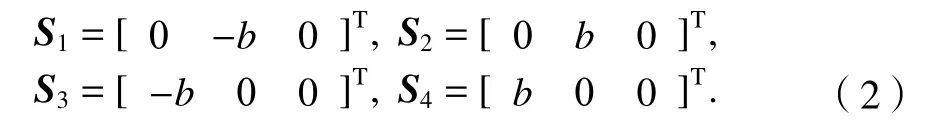
2-UPR/2-RPU 并联机器人的驱动位于P副处为机构的主动关节位置，设机构末端位置点o处的坐标矢量为：P=(x,y,z)T，各支链的移动位移量为li(i=1,2,3,4)。采用Z-Y-Z型姿态欧拉角(α,β,γ)及坐标变换原理可以将旋转变换矩阵表示为

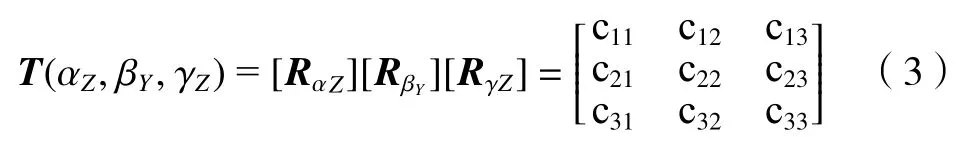
式中：c11=cosαcosβ，c21=sinαsinβ，c12=cosαsinβsinγcosγsinα，c13=cosαsinβcosγ+cosγcosα，c22=sinαsinβ sinγ+cosγcosα，c23=sinαsinβcosγ-cosαsinγ，c31=-sinβ,c32=cosβsinγ，c33=cosβcosγ。RαZ、RβY和RγZ分别代表绕Z轴、Y轴和Z轴的转换矩阵，因此2-UPR/2-RPU 并联机器人可以根据机构位姿确定动平台点Mi由o-xyz坐标系转换到O-XYZ坐标系中的坐标如下

根据图1 可得如下闭环矢量方程

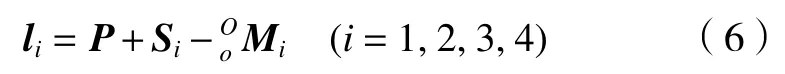
式中：li为各支链中移动关节的矢量；Si表示从点O到点Si的矢量；定义矢量ei(i=1,2,3,4)分别代表转动关节Mi中心线的且模为1 的矢量。

由几何关系可得机构的约束条件

由机构的几何特征及两点的距离公式可得

对式（1）～（7）整理可得

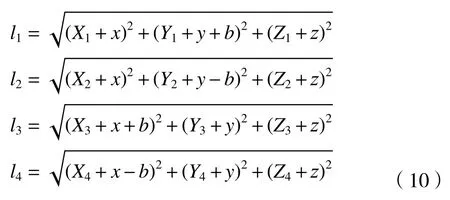
因此，由式（1）～（10）结合MATLAB 程序求解可得到2-UPR/2-RPU 冗余并联机器人的位置反解；而冗余驱动并联机器人的反解求解过程是已知位姿求解各支链移动副的位移量li，而且冗余并联机器人的反解求解过程相对简单且其解具有唯一性；2-UPR/2-RPU 冗余并联机器人的位置正解与其反解求解过程正好相反，是已知驱动副Pi的驱动位移来求解动平台位姿。

2 基于拉格朗日方程的动力学建模

2-UPR/2-RPU 冗余并联机器人是由多个刚体构成的组合系统，其拉格朗日算子L表述为

式中：T为动能，V为势能。机构系统的运动方程以拉格朗日方程表示为

式中：n为杆件总数；qi为系统的广义坐标变量；为广义速度；Fi为影响第i个广义坐标的广义力或广义力矩。将拉格朗日算子代入式（12）得

因此，机构的系统势能V仅是关于qi的表达式，而动能T是关于qi，及时间t的表达式，接下来求解机构各个构件的速度。而机器人动平台的速度可以用如下矩阵表示

式中：Kp为动平台速度关于广义速度的映射关系矩阵，其形式为

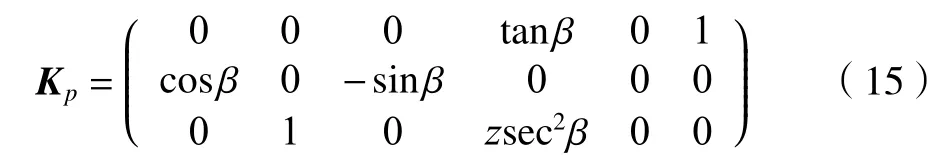
而vp=(ωT)T为动平台的速度矢量，ω为动平台的角速度矢量，为动平台的线速度矢量。

而2-UPR/2-RPU 并联机器人动平台中心点的加速度可以通过对式（14）求导得到

下面以分支1（UPR 分支）为例阐述并联机构分支速度分析方法，依据末端执行器的运动可知分支1 转动副对应转动轴的速度为

式中：a为动坐标系原点指向转动副中心的向量。根据速度合成定理将vRi映射到驱动杆轴向可得主动速度

式中：zLi是驱动支链轴向单位矢量，Li为移动副杆件长度。根据冗余并联机构的几何位置关系，转动副的速度可以用下式表述

式中：ωLi为杆件角速度；将式（19）两边同时叉乘zqi，同理推导出杆件的质心速度vZi

根据式（11）～（21）即可求得到机构的广义力，但逆动力学建模需要求解机构的主动力，因此使用虚功原理描述机构的主动力与广义力间的关系，设机构的广义坐标为θ、δ、ψ，则其对应的广义力和虚位移分别为qθ、qδ、qψ和Δθ、Δδ、Δψ。因此在移动副驱动力Fi驱动下，机构的总虚功为

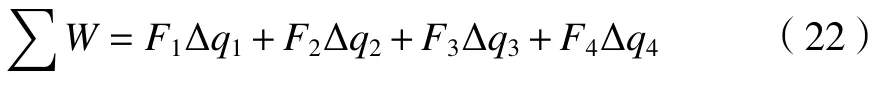
因此可以得到：

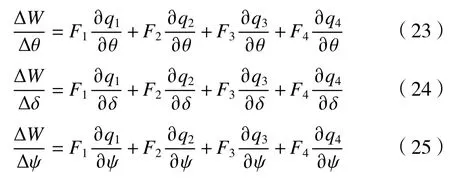
由式（23）～（25）可得广义力和驱动力间的雅可比矩阵JT为

将式（12）～（26）联立可得并联机构的动态方程

即为2-UPR/2-RPU 冗余并联机器人的逆动力学方程。

3 基于螺旋理论的动力学建模

下面本文运用螺旋理论对2-UPR/2-RPU 冗余并联机器人并以分支1（UPR）为例进行速度和加速度分析。首先建立如图2 所示的螺旋系

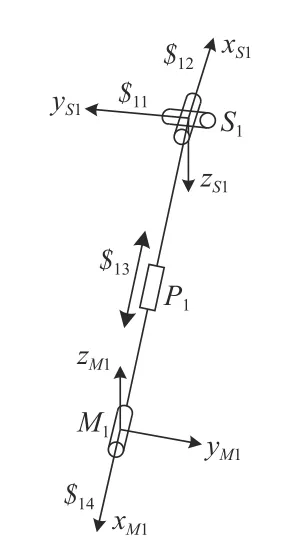
图2 UPR 分支简图

设点M1的坐标为(xM1,yM1,zM1)T，则分支1 的螺旋系有

用ω1i(i=1,2,3,4)表示分支1 各个关节速度，则式（14）可表示为

其矩阵形式为

因此2-UPR/2-RPU 冗余并联机器人每个分支的驱动关节速度可以表示为

进一步化简可得分支i中第j个关节的速度与各个分支驱动速度之间的关系

因此分支i中第j个关节的质心速度螺旋为

式中：dijCe为从原点到分支的i中第j个杆件质心点的位置矢量。在定坐标系下分支1 末端加速度可以表述为

因此，由式（34）可以推导出分支i中第j个杆件的速度螺旋为

下面根据虚功原理来推导该机构动平台受到的力和力矩为

式中：动平台质量为mp，重力加速度为g，动平台质心线加速度为apCe，动平台相对于定坐标系的惯性张量为IOp，动平台角速度为ωp。而作用在分支i上第j个杆件质心处的力螺旋为

因此2-UPR/2-RPU 并联机器人的总功为

由虚功原理可得

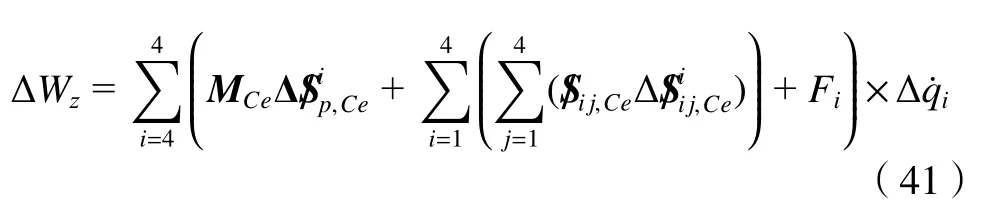
式（40）～（41）中：Δvi j,Ce和为虚速度且其值为任意值，根据虚功原理2-UPR/2-RPU 并联机器人的总虚功始终为零，故有

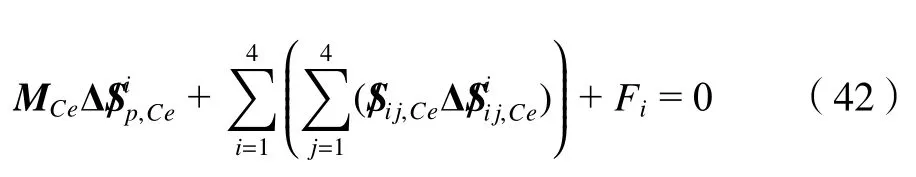
因此由式（42）可计算得2-UPR/2-RPU 并联机器人驱动副的驱动力数值。

4 两种方法下动力学仿真分析对比

接下来在SW 建模软件中建立2-UPR/2-RPU 并联机器人的3D 模型，以Parasolid(*.x_t)文件导入动力学仿真软件ADAMS 中，通过ADAMS 来验证采用朗格朗日方法和螺旋理论方法所建立的冗余2-UPR/2-RPU 并联机器人动力学模型的正确性，在ADAMS 中建立如图3 所示的动力学模型添加构建关系并设置各项参数。

图3 并联机器人ADAMS 动力学模型

设动平台和定平台的边长分别为a=250 mm 和b=400 mm，及动平台中心点轨迹方程为

式中：t0为期望持续时间，其值为0.5。在软件MATLAB 的中建立并联机器人的模型，以运动学和动力学模型为基础，编程得到并联机构的算法，将以螺旋理论和拉格朗日法建立的并联机器人动力学方程为输入，仿真后得到机器人的分支链驱动力与ADAMS 输出的动力学仿真分支链驱动力数据并得到图4 所示的在动平台中心点轨迹方程驱动下的驱动力随时间变化图。

从图4 中可得，基于拉格朗日方程和螺旋理论求解的支链驱动力和ADAMS 软件仿真求解的支链驱动力数值变化曲线整体是一致的，从而验证了采用这两种方法所建立的2-UPR/2-RPU 并联机器人的动力学模型是正确的，在运动周期内，最大驱动力出现在驱动杆支链1 处为269.3 N。同时数据也存在区别，下面对两种方法的求解结果进行误差分析，利用MATLAB 编程功能将图4 中计算数据按照以下计算方法：给定轨迹数值与理论值之差在该时刻驱动力所占ADAMS 理论值的百分比进行误差分析，求解得到2-UPR/2-RPU 并联机器人的各链驱动力误差随时间变化曲线如图5。

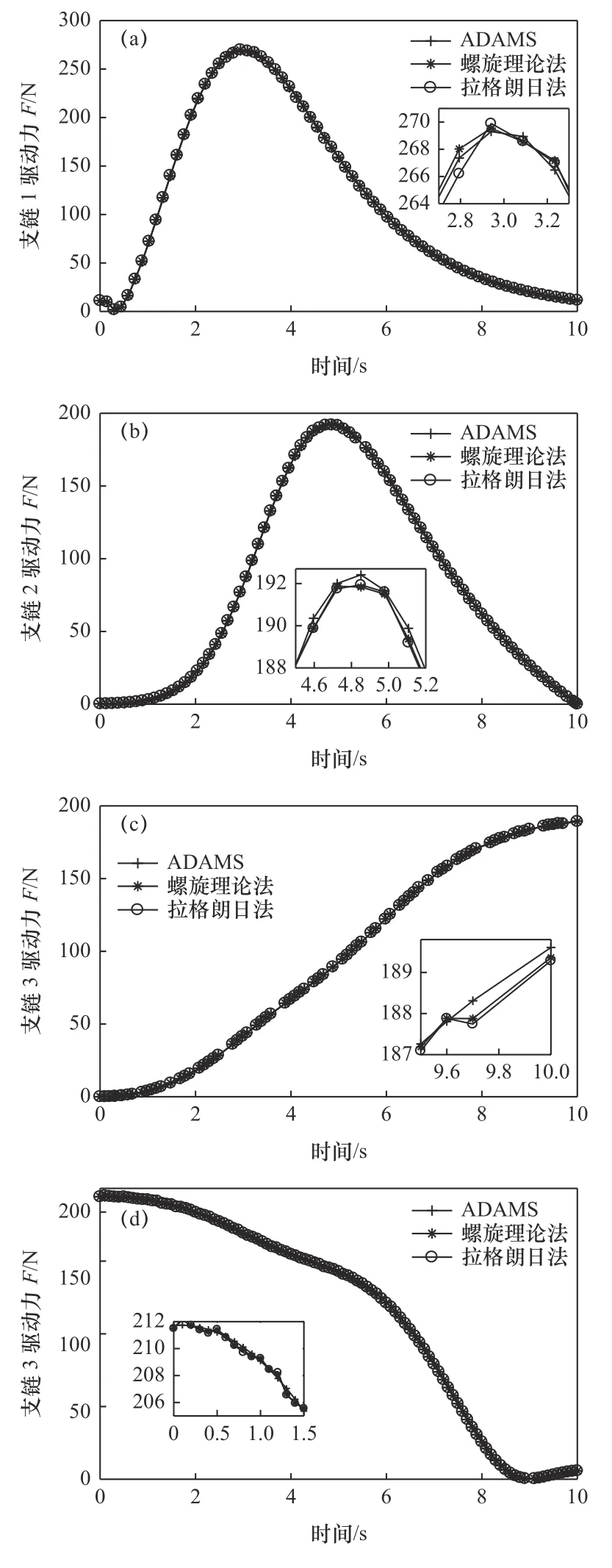
图4 各支链驱动力求解结果曲线

从图5 可以看出，各支链中采用螺旋理论法动力学建模求解出的驱动力误差的最大值和最小值为：驱动杆1 的驱动力相对最大误差为0.43%和0.452%、约0.515 N 和0.527 N；驱动杆2 的驱动力最大误差为0.34%和0.381%，约0.580 N 和0.649 N；驱动杆3 的驱动力相对最大误差为0.281%和0.295%，约0.324 N 和0.336 N；驱动杆4 的驱动力相对最大误差为0.181%和0.252%，约0.381 N 和0.529 N；因此，螺旋理论法和拉格朗日法求解结果相对误差较小，并且处于合理范围。

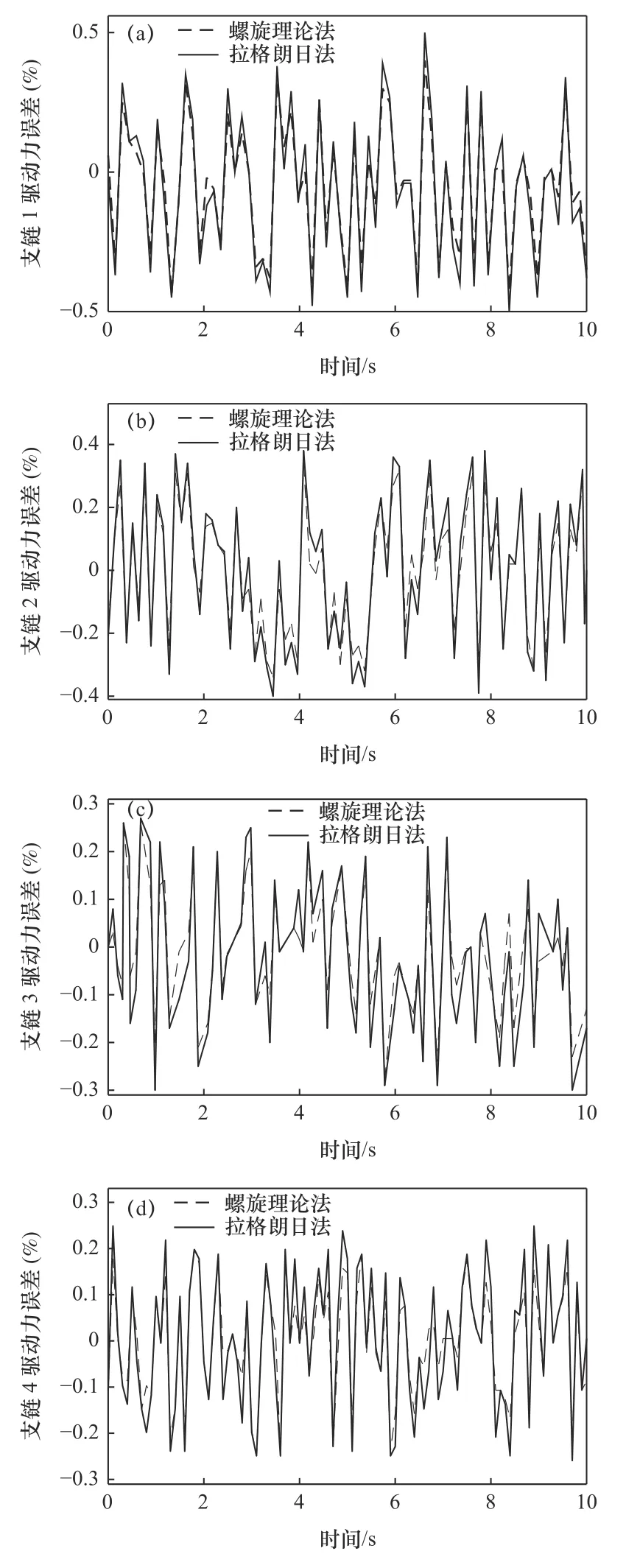
图5 各支链驱动力误差图

而在使用MATLAB 软件进行数值求解后得出了这两种方法的优缺点：拉格朗日方程的建模过程相对简单，但在MATLAB 软件进行编程数值求解时计算量大且费时；螺旋理论法模型建立过程简单、逻辑清晰，在数值求解时计算量小且速度快。

5 结语

（1）采用封闭矢量法建立了并联机器人的运动学反解方程，求解过程简单且解具有唯一性。

（2）采用螺旋理论对2-UPR/2-RPU 并联机器人各关节和杆件的速度和加速度进行分析，建立并联机器人的动力学模型。

（3）采用拉格朗日法求解了并联机器人机构部件的速度关系并建立了其动力学模型。

（4）通过在MATLAB 中编程得到与ADAMS软件的动力学仿真结果对比图并进行仿真验证和误差分析。结果表明：螺旋理论建立的动力学模型精度相对较高、方法方便理解、计算简单、精度高、更适用于少自由度并联机构动力学模型的建立和机构动力学的控制；满足磨床打磨曲面的精度要求，为机构的实践应用提供了可靠的理论依据并奠定了重要基础。