基于MATLAB 的6R 机械臂运动学的仿真研究＊

胡宇航 张尚盈② 张晓艳

（①武汉工程大学机电工程学院，湖北 武汉 430205；②武汉誉琼科技有限公司，湖北 武汉 430205）

近些年机械臂广泛应用于多个生产领域，这是因为它使用方便、动作灵敏，并且能适应各种复杂多变的工作环境，能有效地减少劳动力、提高生产效率。在工业拆卸及大物件搬运等起重比要求高的环境中，大多使用液压机械臂。

为了提高液压机械臂的结构性能、作业精度等，其运动学的研究尤为重要。对于机械臂的建模及正逆运动学的研究方法选择上，不论是D-H 建模还是其他的建模方式；数值解析法还是几何法，或是神经网络、遗传算法求逆解，都各有利弊。大部分专家学者在进行对机械臂运动学的研究中都采取了不同的方法。对机械臂建模而言，郭发勇等[1]使用一种实体建模的方式（CFDH）使机器人建模更直观准确，但建模步骤会繁琐一些；Li F T 等[2]采用改进的D-H 法和几何映射算法对液压机械臂建模。对运动学分析而言，郭志强等[3]和赵修琪等[4]采用矩阵逆乘的方式求逆解，此过程易懂明了，但出现了漏解现象；张普行等[5]用空间几何求反解，避免了大量矩阵乘和求矩阵逆；Peng J Q 等[6]对6 自由度机械臂划分成两个3 自由度，用解析法对其求逆解；党浩明等[7]用中间变量替代齐次矩阵连乘，有效缩短逆解运算时间；Zarrin A 等[8]提出一种逆运动学的优化几何解法，在笛卡尔坐标系下增加2 个角度输入，增加机械臂工作空间，优化其效率，逆运动学求解大大降低了定位误差；Duka A V 等[9]采用基于神经网络方式求逆解，并对其轨迹进行跟踪验证，结果非常稳定。

本文以6R 液压机械臂为研究对象，针对其正逆运动学进行研究和分析。首先，用改进的D-H 参数法构建机械臂运动学模型及正运动学方程，运用几何法和解析法结合的方式求出运动学逆解，然后调用机器人工具箱对正逆解进行求解，分析对比计算值与真实值。最后，通过关节空间轨迹规划进行仿真，验证此建模及运动学分析的机械臂运动平稳有效，为之后运动规划及实时控制打下坚实基础[10]。

1 机械臂运动学分析

1.1 机械臂基本结构及建模

液压机械臂是一款6R 关节串联机械臂，其三维模型如图1 所示，它的主要组成包括腰部（回转）、大小臂（俯仰）以及手腕等部分，各相邻杆件通过转动关节连接，在工业拆卸、搬运等领域具有广泛的应用。机械臂全液压驱动，除肩部采用直线液压缸、腕部旋转采用液压马达，其余关节全部采用摆动液压缸。

图1 液压机械臂三维模型

根据图1、2 的机械臂三维模型及其尺寸参数，通过改进的D-H 参数法，建立机械臂坐标系，i-1系与i系之间的变换关系可以用平移和旋转来表示。其建模的具体步骤如下：

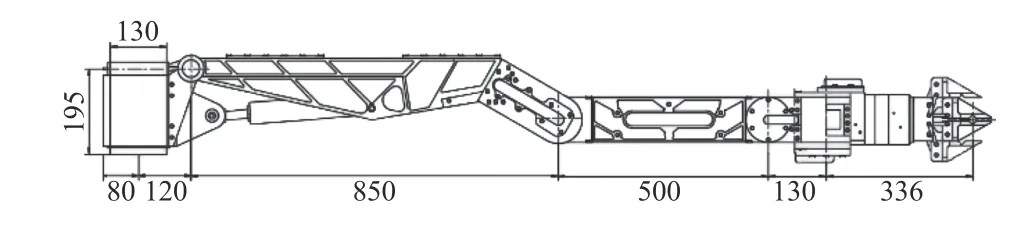
图2 液压机械臂平面尺寸

（1）令i-1系绕zi-1轴旋转 θi，使xi-1与xi平行，其算子为Rot(zi-1,θi)。

（2）沿着zi-1轴平移di，使xi-1轴与xi轴重合，其算子为Trans(0,0,di)。

（3）沿着xi轴平移ai-1，使二者原点重合，其算子为Trans(ai-1,0,0)。

（4）沿着xi轴旋转 αi-1，使得i-1系和i系重合，其算子为Rot(xi,αi-1)。

构建的机械臂坐标系简图如图3 所示，构建的连杆参数及关节变量如表1 所示，其中 αi-1表示连杆坐标系之间的扭转角度，θi表示各关节的旋转角度，ai-1表示相邻关节之间的连杆长度，di表示相邻连杆之间的偏移量。在表中各参数之中，只有 θi为变值，ai-1、αi-1和di均为定值。

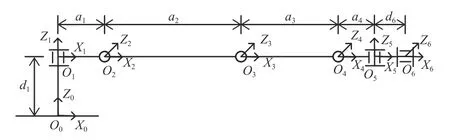
图3 机械臂坐标系简图

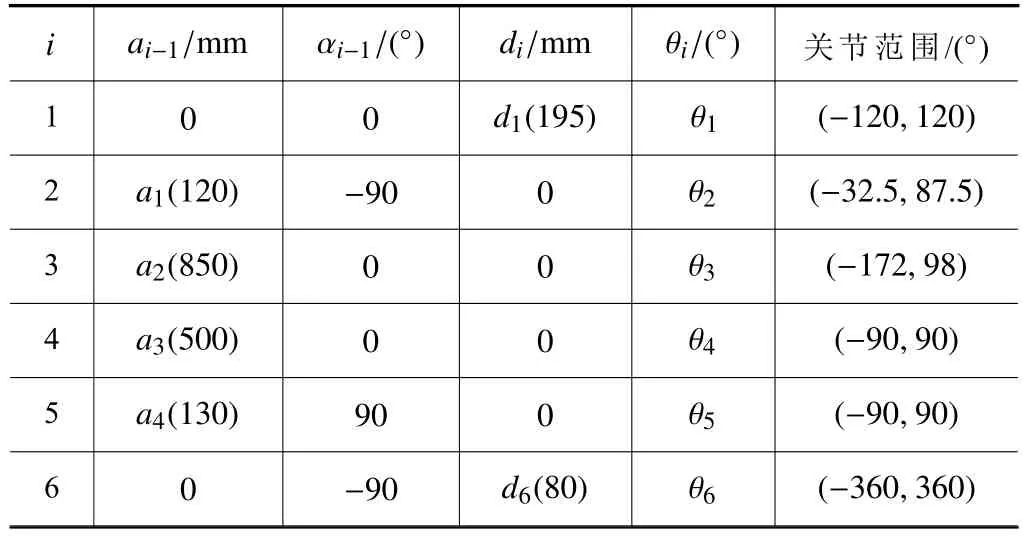
表1 液压机械臂D-H 参数

1.2 机械臂运动学正解

机械臂的正运动学是通过两连杆坐标系间的变换矩阵相乘得到末端位姿矩阵的过程。由于本文运用改进的D-H 参数法，其变换矩阵的通式用式（1）表示。

将表1 中各连杆的D-H 的4 个参数代入式（1）中，可依次得到如下各连杆变换矩阵。

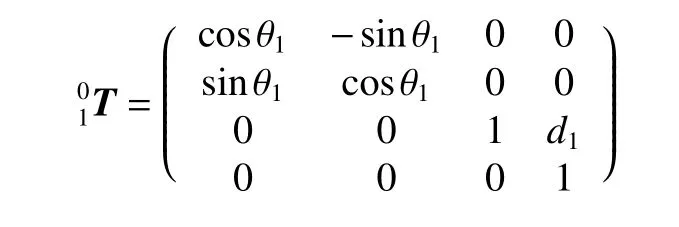
将以上各连杆变换矩阵依次相乘得到机械臂正解，如式（2）所示。

式（2）中：

其中：c234=cos(θ2+θ3+θ4)，s234=sin(θ2+θ3+θ4)，c23=cos(θ2+θ3)。

1.3 机械臂运动学逆解

机械臂运动学求逆解是通过已知的末端位姿矩阵来求解各个关节的旋转角度。求逆解的方法一般包括几何法、解析法等。几何法一般是将D-H 参数通过空间几何转换到平面上来求解；而解析法是通过变换矩阵得到的三角函数方程来求解。本文则通过几何法和解析法结合的方式来求解机械臂运动学逆解，这样可以大大减少其计算量。

（1）计算θ1,θ5,θ6

由于关节2～4 是俯仰关节，通过俯视角度观其始终在一条直线上。关节5 为偏摆关节，关节6 为回转关节连接在关节5 上，可知关节6 相对于关节5 的相对位姿是固定的。当给定末端位姿，可通过齐次变换得到关节5 相对于基座下的位姿，再通过图4 就能确定 θ1的表达式。

图4 关节5 在基座坐标系下的投影

通过式（3）可得

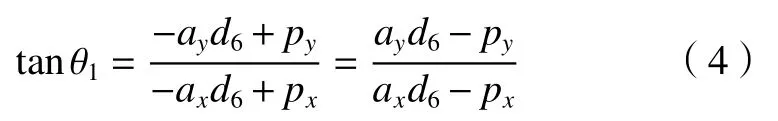
通过式（4）可得

或

（2）计算θ2,θ3,θ4

再根据（1,4）和（3,4）相等后移项得

令X1和X2分别与式（12）右部分相等得

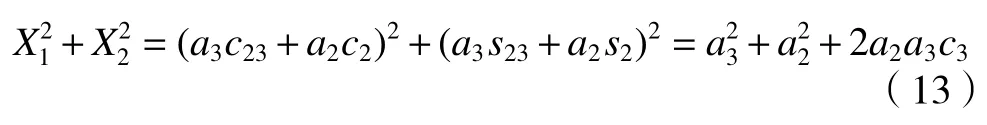
从而通过（13）求解θ3

根据式（12）～（14）可求出θ2

再根据式（13）～（15）可求出θ4

通过以上几何法和解析法结合的方式已求出此液压机械臂全部关节角，从以上各式可看出存在多解的情况，经过组合可生成8 组逆解，具体的求解流程如图5 所示。大部分的机械臂都会存在多个逆解，会让机械臂的末端位姿有多种选择。但是在实际运动过程中，要充分考虑到机械臂参数的约束，会有部分逆解在机械臂可达空间之外，或是末端位姿不符合操作任务的要求，所以对求得的逆解需要进行验证。

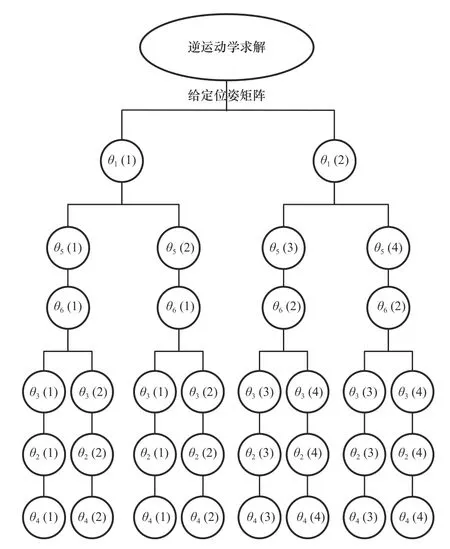
图5 运动学求逆解流程图

2 机械臂运动学仿真

2.1 建立运动学模型

在MATLAB 软件中，使用机器人工具箱Robotics Toolbox 对机械臂进行运动学建模，它包含机器人所需要的多种运动学函数。根据表1 所给出的数据，运用机器人工具箱对机械臂建模，得到的初始模型如图6 所示。

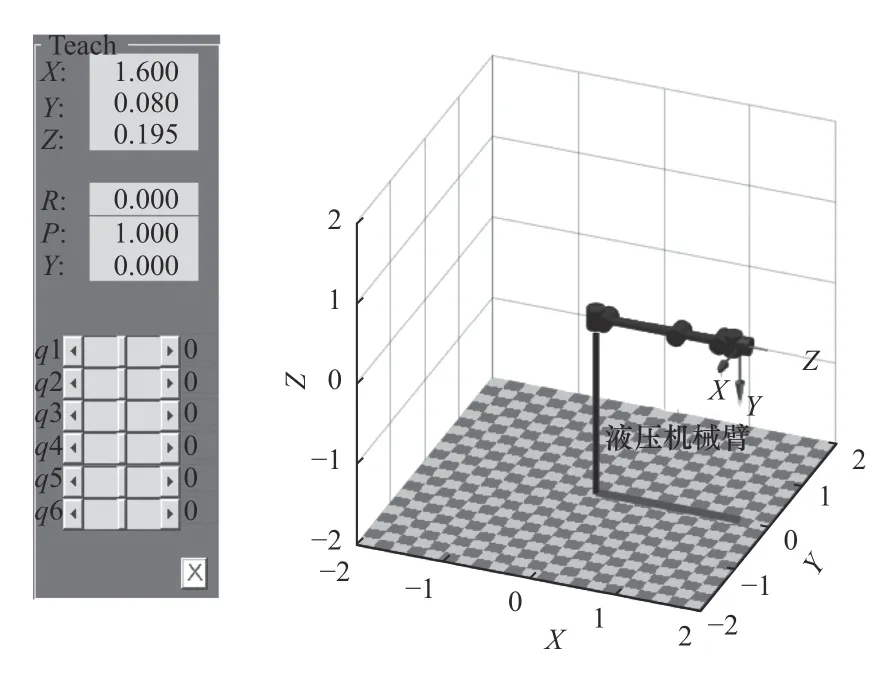
图6 机械臂初始姿态

2.2 机械臂正运动学验证

对机械臂进行正运动学的验证，只需要将一组关节角代入式（10），得到的位姿矩阵与MATLAB得到的是否一致，若一样则正运动学验证正确。

取随机一组关节角q1=[0 0 0 0 0 0]，代入到运动学正解公式中得到末端姿态矩阵T1，与机器人工具箱所得到的末端位姿矩阵（如图6）一样，验证了机械臂正运动学方程与运动学模型的正确性。

2.3 机械臂逆运动学验证

取q2=[30 60 45 75 45 120]*pi/180代入到机器人工具箱中进行求解，可得到末端位姿矩阵T2

将上述得到的位姿矩阵代入到（1.3）节中的计算公式，可计算出对应的运动学逆解。在MATLAB对机械臂逆解计算得出结果如表2 所示。

表2 运动学逆解数值

根据表2 的数据可知，对于每组末端位姿均可求出8 组逆解。当然在实际应用中，对机械臂的约束不同，机械臂能到达的关节角度只会是其中的一部分。经过数据对比，发现q2的取值与表2 第一组一致，至此验证了建立此种逆运动学的正确性。

2.4 轨迹规划及仿真

这里所指的轨迹规划方法是指机械臂在运动时，对其位置、角速度及角加速度进行规划，通过得到的曲线观察其具体的运动状态[11-12]。

选用关节空间轨迹规划，在空间中选择任意两点，在机器人工具箱中调用函数对机械臂进行轨迹规划。设关节空间中初始点所对应的关节转角为q1=[0 0 0 0 00]，末端点所对应的关节转角为q3=[45 -60 90 60 -36 -30]，得到的机械臂末端运动轨迹如图7 所示。

图7 机械臂末端运动轨迹

需要对机械臂的6 个关节进行分析，分别对其位移、角速度及角加速度进行仿真。由图8 可知，机械臂在运行过程中，6 个关节所有关节的角位移、角速度、角加速度随时间变化曲线能平稳运行，不存在间断和突变。由以上分析可知此液压机械臂及末端执行器可连续平稳的完成作业任务。

图8 液压机械臂各关节仿真曲线

3 结语

本文以液压机械臂为研究对象，基于改进D-H法对其进行运动学建模，建立正运动学方程。通过空间几何法和数值解析法结合的方式求出其8 组逆解，在MATLAB 编写程序验证了正逆运动学的正确性。借助机器人工具箱，在关节空间中进行机械臂运动轨迹的仿真，通过观察各关节角位移、角速度和角加速度的平滑曲线，验证了机械臂参数的合理性。