基于“六何”认知策略的教学设计与思考——以“余弦定理”教学为例

浙江师范大学物理与电子信息工程学院 孔胜涛（邮编：321004）

所谓“六何”认知策略是周莹教授针对数学教学“缺头少尾烧中段”的现象提出的一种认知策略，即“从何、是何、与何、如何、变何、有何”的认知策略[1]. 近几年，笔者在数学教学中，多次尝试运用“六何”认知策略进行课堂教学，取得了较好的教学效果.

下面以人教版高中数学普通教科书必修第二册第六章中“余弦定理”的教学为例，介绍基于“六何”认知策略的教学设计的一些做法和思考，以期为高中数学的定理课堂教学提供参考.

1 教学过程

1.1 追溯“从何”

“从何”是指新知从哪里来？基于对“余弦定理从哪里来?”的思考，可以创设问题情境如下：

问题1 修建一条高速铁路时，要开凿隧道将一段山体打通，现要测量该山体底侧两点间的距离，也就是：如图1，要测量该山体两底侧A，B两点间的距离. 同学们能想出解决这个问题的方法吗？

问题2 如图2，在山体的远处选一点C，然后量出AC=b，BC=a，再测出∠ACB=α，如何求出AB的长度呢？

图1

图2

设计意图通过创设问题情境，引出新问题，旨在激发学生去探究新知，这不仅有利于培养学生学习数学的兴趣和积极性，而且有利于培养学生数学抽象、数学建模的核心素养.

1.2 把握“是何”

“是何”是指新知的本质特征是什么？基于对“余弦定理的本质特征是什么？”的思考，可以提出“是何”问题串如下：

问题3 三角形以角来划分，有哪些类型的三角型？同学们还记得初中学过的勾股定理吗？

问题4 在任意的锐角△ABC中，你能用边a，b和角C表示边c吗？

生1：可以，如图3，过点A作垂线交BC于D，设AC=b，AB=c，BC=a，则AD=bsinC，CD=bcosC，BD=BC-CD=a-bcosC.

图3

所以c2=AD2+BD2= (bsinC)2+(a-bcosC)2=a2+b2- 2abcosC.

即c2=a2+b2- 2abcosC.

问题5 在任意的角C为钝角的三角形和角C为直角的三角形中，是否都有c2=a2+b2-2abcosC仍然成立呢？由此你能得到什么结论？

设计意图从余弦定理的结构特征出发，通过问题3,4,5 引导学生类比直角三角形中的勾股定理，旨在让学生发现勾股定理是余弦定理的特例，余弦定理是勾股定理的推广，这有利于学生把握余弦定理的特点，发现余弦定理的本质.

1.3 连接“与何”

“与何”是指新知与旧知有怎样联系及不同？基于本节课是在系统学习勾股定理、平面向量及平面解析几何初步的基础上展开的，可以提出“与何”问题串如下：

问题6 同学们还记得平面向量数量积的几何意义吗？

问题7 同学们能尝试用向量法证明余弦定理：在任意△ABC中，都有c2=a2+b2-2abcosC，a2=b2+c2-2bccosA，b2=c2+a2-2cacosB成立吗？

图4

同理可证：a2=b2+c2-2bccosA，b2=c2+a2-2cacosB.

问题8 同学们还记得解析几何中的两点间距离公式吗？

问题9 同学们能尝试用坐标法证明余弦定理：在任意△ABC中，都有c2=a2+b2-2abcosC，a2=b2+c2-2bccosA，b2=c2+a2-2cacosB成立吗？

生3：老师，我能用坐标法证明. 建立如图5所示的直角坐标系，则A(bcosC,bsinC)，B(a,0).

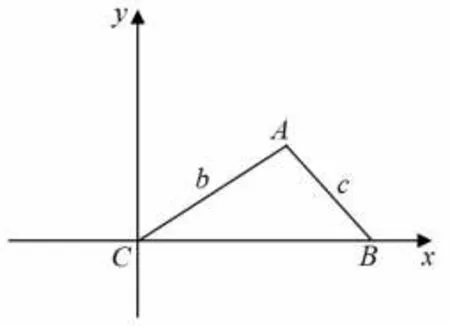
图5

根据两点间的距离公式，可得

c2=(bcosC-a)2+(bsinC-0)2=a2+b2-2abcosC,

即c2=a2+b2-2abcosC.

同理可证：a2=b2+c2-2bccosA，b2=c2+a2-2cacosB.

设计意图通过问题6,7,8,9 引导学生探究余弦定理的二种不同证法，旨在强化余弦定理与其他旧知识的联系，从而促进新旧知识间的融会贯通. 这有利于提升学生的逻辑推理和数学运算等核心素养.

1.4 操作“如何”

“如何”是指新知如何学以致用？基于对“余弦定理如何学以致用？”的思考，可以提出“如何”问题串如下：

问题10 在如图2 所示的△ABC中，测得a=500 米，b=400 米，C=120°，求AB的长度（边长精确到0.1 米）.

生4：由余弦定理，得

AB2=a2+b2-2abcosC=5002+4002-2×500×400×cos 120°=6.1×105，

问题11 在△ABC中，已知a=3，b=5，c=7，求角C的大小.

生5：由余弦定理，得

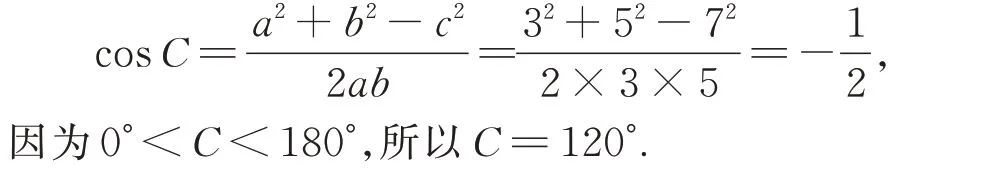
设计意图通过问题10,11 引导学生分析问题、解决问题，使学生掌握应用余弦定理解任意三角形的方法，旨在凸显余弦定理的应用价值，这有利于提升学生数学运算和数据分析的核心素养.

1.5 重视“变何”

“变何”是指怎样变式拓展？基于对问题10,11“变一变又会怎样？”的思考，提出“变何”问题串如下：

设计意图问题12,13 分别是问题10,11 的变式题，通过问题12,13 的拓展练习，旨在拓宽学生的解题思路，这有利于培养学生的创新思维能力和变式能力.

1.6 挖掘“有何”

“有何”是指学完新知后有哪些收获、体会和困惑？通过对“学完余弦定理后有哪些收获、体会和困惑？”的思考，可提出“有何”问题串如下：

问题14 回顾整堂课，我们一起来总结一下本节课学习的主要内容有哪些？

问题15 通过本节课的学习，你有什么收获？对余弦定理有什么认识？对本节课是否还有疑问？

设计意图通过问题14,15 引导学生从多角度对整堂课进行一次回顾与梳理，旨在培养学生的概括能力和理性精神.

2 教学思考

从上述的“余弦定理”教学过程中，我们不难发现，运用“六何”认知策略进行高中数学教学的意义主要在于以下两点：

2.1 有利于提升学生的核心素养

在基于“六何”认知策略的高中数学教学中，“六何”能把新知识的来龙去脉问题化、操作化和完整化.“从何、是何、与何、如何、变何、有何”的具体内容，即新知从哪里来？新知的本质特征是什么？新知与旧知有怎样联系及不同？新知如何学以致用？怎样变式拓展？学完新知后有哪些收获、体会和困惑？这“六何”具有思考的根基性、层次性和连贯性，逐次生长、提升和拓展，有利于学生体会新知识形成的过程，有利于促进学生对新知识的再创造，从而有利于提升学生的核心素养. 因此，基于“六何”认知策略的高中数学教学有利于提升学生的核心素养.

2.2 有利于提升学生的提问能力

在基于“六何”认知策略的高中数学教学中，围绕“六何”设置问题，以“从何”引入新课，以“是何、与何、如何、变何”引领学生学习和思考，以“有何”总结整节课的学习内容，这些何何递进的问题贯穿于整个课堂教学过程. 俗话说“看过问题三百遍，不会解题也会问”，在这样的课堂教学氛围下，学生耳濡目染，问题意识会不断增强，提问能力就会不断提升. 因此，基于“六何”认知策略的高中数学教学有利于提升学生的提问能力.