陡峻山区输电铁塔结构风荷载分布特性分析

汪 涛， 赵 震， 刘鸿熹， 聂义民， 邵尤国

（国网江西省电力有限公司经济技术研究院，南昌 330096）

我国幅员辽阔地、形复杂多样，地形走势由高向低并自西向东分布，其中高原与盆地地形占我国总面积的45%左右. 崎岖地形为输电线路架设增加了一定困难，而架设在山区的输电杆塔塔体高、跨距大，导致其结构柔性较强，对风荷载的反应较敏感［1-2］. 陡峭的山区受其地形影响，其风能力往往较平原地区等级高.当输电杆塔受力达到其极限时，往往发生疲劳损伤或者倒塌情况，造成大面积电网瘫痪［3］，影响人们日常生活的同时会造成一定经济损失. 近年来针对输电杆塔受风力荷载研究方法众多，如王飞等［4］利用谐波合成方法获取脉动风速时程，并依据输电杆塔空间结构特征使用模拟软件对其受风荷载展开研究，但该方法仅考虑输电杆塔位移、轴向应力和风速之间的关系，并未从风荷载力分布角度对其进行研究，因此存在片面性. 柯世堂和王浩［5］则从不同结构与形状的输电杆塔入手，通过设置各种工况，使用风洞实验方式并依据特征角度和气动力值之间的映射关系，利用数学计算模型完成输电杆塔受风力荷载分析，但该方法所用风洞实验对实验环境要求极高，杆塔结构分布或者位置变换均影响其最终研究结果，因此实用性不强.

面对上述情况，本文提出陡峻山区输电铁塔结构风荷载分布特性分析方法. 以某山区输电杆塔为原型，使用APDL编写输电杆塔特征参数模板，利用Ansys有限元软件构建输电杆塔参数化模型；使用数学计算方式计算山区输电杆塔风荷载，获得铁塔结构风荷载分布特性. 本文的创新点为有限元建模部分以某山区输电杆塔为原型保证了模型的真实性和可靠性；APDL参数模板中利用循环语句连接节点对输电杆塔构件进行拼接，保证了模型的完整性；数学计算部分利用风压高度变化系数修正不同高度的平均风压，保证获得的荷载分布特征的准确性. 本研究为陡峻山区输电杆塔架设提供较为科学的依据.

1 输电铁塔结构风荷载分布特性

1.1 输电杆塔参数化有限元建模

参数化建模方式是有限元建模方式的一种，其宗旨是利用可变参数建立模型［6-7］. 为提升山区输电杆塔建模效果，使用参数化设计语言APDL 编写输电杆塔特征参数模板，利用Ansys有限元软件构建输电杆塔参数化模型.

架设在陡峻山区的输电杆塔总量和塔体数值均较大［8-9］，以某山区输电杆塔为原型构建其有限元模型，该杆塔参数如表1所示.

在有限元软件内，依据表1 内山区输电杆塔参数，使用参数化设计语言APDL将输电杆塔具备相似性和规则性的螺栓、法兰等编写成参数化模板［10］，并依据各参数化模块需求，使用参数化模板对输电杆塔进行拼接，最终得到输电杆塔有限元模型，依据上述思想，输电杆塔有限元建模流程如下.

表1 山区输电杆塔参数Tab.1 Parameters of transmission towers in mountainous areas

第一步：将山区输电杆塔结构类型进行分类处理，剔除掉不影响输电杆塔结构的多余结构类型［11-13］，并依据输电杆塔不同结构划分基本结构模块.

第二步：按照山区输电杆塔模块结构特征，使用特征提取方法提取该特征并定义其特征参数.

第三步：依据输电杆塔特征参数，使用参数化设计语言APDL命令流文件在有限元软件工作面内建立对称节点，利用循环语句连接节点构建输电杆塔杆构件［14-15］. 依据输电杆塔杆构建材料特征，定义有限元内输电杆塔构建材料属性和单元类型后，建立输电杆塔参数化模型库.

第四步：按照输电杆塔形状，将其特征参数具体数值化，并从输电杆塔参数化模型库内调取相应模块，按照输电杆塔各个模块间关联关系，经过拼接后获得完整输电杆塔模型.

将上述步骤简化处理后，得到山区输电杆塔有限元模型构建流程，如图1所示.

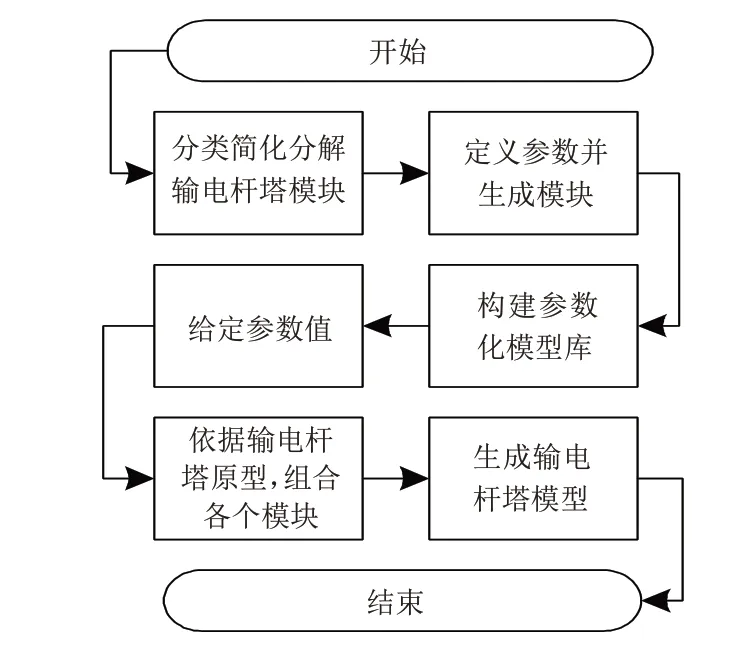
图1 输电杆塔参数化有限元建模过程Fig.1 Parameterized finite element modeling process of transmission tower

依据上述输电杆塔参数化有限元建模过程，构建山区输电杆塔有限元模型如图2所示.

图2 输电杆塔模型Fig.2 Transmission tower model

1.2 风荷载计算

使用数学计算方式计算山区输电杆塔风荷载，令顺风向风速由B(z,t)表示，其表达公式如下：

式中：z、t分别表示高度和时刻；bˉ(z)表示输电杆塔高度为z处的平均风速；b(z,t)表示脉动风速.使用伯努利方程计算时刻为t时，输电杆塔位置为z处的风压数值，其表达公式如下：

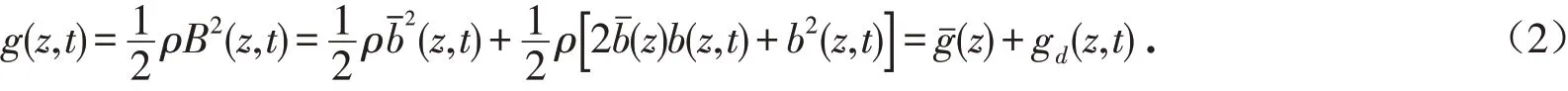
式中：g(z,t)表示风压数值；gˉ(z)表示平均风压；gd(z,t)表示脉动风压；ρ表示阶数.将脉动风压剔除高阶项可得：

式中：vˉ(z)为脉动增大系数；v(z,t)为非平稳峰值函数，当输电杆塔受到脉动风压荷载时，受输电杆塔结构形状影响［16-19］，导致风压大小不同，此时使用体型系数修正脉动风压，其表达公式如下：

式中：μs表示体型系数.

将平均风作用在输电杆塔结构上的荷载看作静力荷载，利用风压高度变化系数修正不同高度的平均风压［20-21］，此时输电杆塔的平均风压计算公式如下：

式中：μz(z)表示风压高度变化系数；g0表示理想风速风压.

结合公式（4）和公式（5）得到输电杆塔位置处的总风压，表达公式如下：

当使用有限元软件分析输电杆塔风振时，通过节点力传输方式将风荷载施加到输电杆塔结构相对应节点上，即可得到输电杆塔结构节点所受风荷载数值，该数值可由F=wA表示，其中w为风荷载系数，A表示结构受风荷载压力面积. 对于整个输电杆塔来说，风荷载施加点为其塔身上下各取二分之一受风压的面积.

2 实验分析

实验采用有限元软件Ansys建立数值实验模型，系统数据集选择江西省电网公司架设在某山区的输电杆塔参数作为建模基础数据，将数据集写入建模模板中，实验配置如表2所示.

表2 实验配置Tab.2 Experimental configuration

在输电杆塔有限元模型内设置测试点，详情如图3所示.

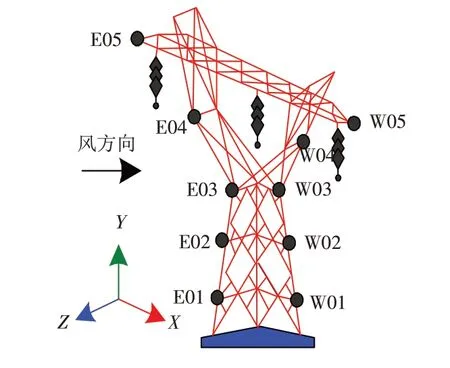
图3 测试点示意图Fig.3 Schematic diagram of test points

依据山区输电杆塔有限元模型，在该模型内对其施加了与输电线垂直方向的风力，风速由10～35 m/s，不考虑输电杆塔自身应力情况下，绘制输电杆塔最大正、负应力变化情况，结果如图4所示.

分析图4 可知，输电杆塔最大应力随着风速的增加而增加. 输电杆塔的最大正应力与最大负应力表现为轴对称关系，可知风速与输电杆塔最大应力之间具备非线性化特征.

图4 风速与输电杆塔最大应力关系Fig.4 Relationship between wind speeds and maximum stresses of transmission tower

在山区输电杆塔有限元模型内模拟35 m/s 的风速，统计不同测试点轴向位移与测试点间轴向应力，结果如表3所示.

表3 测试点位移与应力变化情况Tab.3 Changes of displacements and stresses of test points

分析表3可知，测试点距地面越低，其位移数值越低，对称测试点间的轴应力数值越小. 测试点E01至E05的X方向位移呈现增加趋势，且在测试点E01至E03之间，其X方向位移增加幅度较小，E04和E05测试点位移数值较大，其中E05 测试点位移是E01 测试点位移48.39 倍；与测试点E01 至E05 相对应的W01 至W05测试点的X向位移增长趋势与测试点E01至E05相同，但其X向位移数值稍低于测试点E01至E05；所有测试点Y方向位移均较其X方向位移数值较小. 综上，测试点位置不同其X向和Y向位移数值存在轻微区别，距离地面越近其位移数值越小，究其原因在于输电杆塔深埋地面的主体为三角形，且其存在若干横梁构件组成若干个不同大小的三角形，众所周知三角形结构是最稳定结构，因此该输电杆塔的主体较为稳定，即测试点E01至E03之间结构稳定. 随着输电杆塔测试点距地面距离越远，输电杆塔受其自身重力和风荷载力共同作用，自身稳定性逐渐降低，在风力不变情况下，其在X向和Y向位移数值逐渐增加，导致测试点E04和E05的位移数值越大. 而测试点W01至W05的位移数值低于测试点E01至E05，原因是在同一受力方向上，其距离较测试点E01至E05稍远，风在吹拂的过程中风速会逐渐下降. 从轴应力角度分析，距离地面较近的测试点间所受的轴应力数值较大，原因在于测试点距地面越低其不仅承受风荷载力，还承受输电杆塔构建应力.

为使实验结果更为精准，在山区输电杆塔有限元模型内共模拟10次风吹实验，风力为28、32、35 m/s，统计10次实验时该输电杆塔环向应力峰值和均值，结果如表4所示.

分析表4 可知，山区输电杆塔环向应力受风荷载影响，其所受应力数值表现为自上而下递增趋势，输电杆塔中下部位置承载力数值较大，因此输电杆塔底部结构的稳定性稍差.

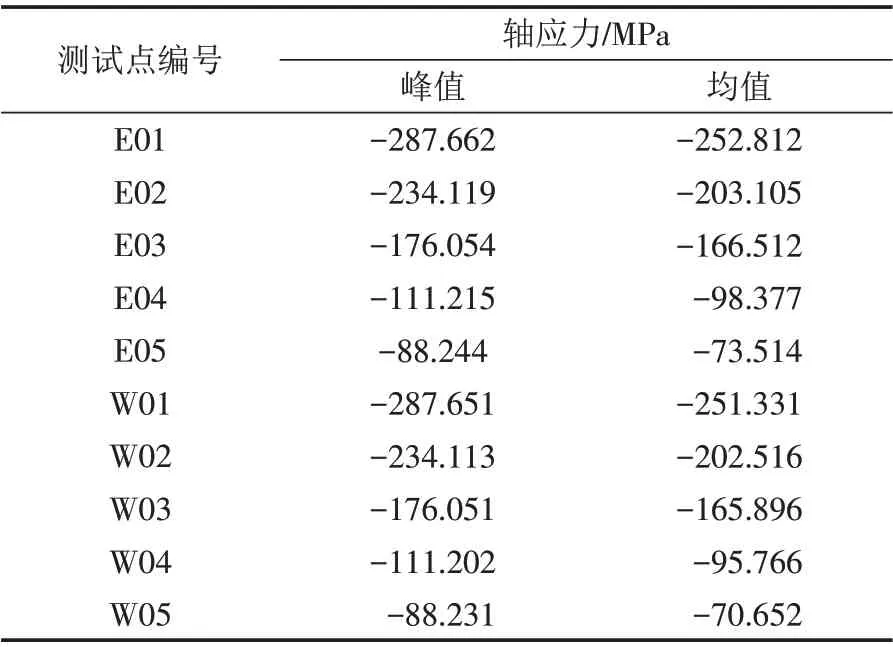
表4 输电杆塔环向应力峰值和均值变化情况Tab.4 Variations of peak values and mean values of circumferential stresses of transmission tower

以山区输电杆塔塔顶为实验目标，测试在不同风速下和不同风角下，输电杆塔塔顶纵向应力变化情况，测试结果如图5所示.

图5 输电杆塔塔顶应力变化Fig.5 Stress changes of transmission tower top

分析图5（a）可知，山区输电杆塔塔顶在风速为0时，塔顶两个测试点的纵向应力数值均为0，随着风速的增加，两个测试点的纵向应力开始向相同方向变化，在风速为0～10 m/s之间时，两个测试点纵向应力向相同方向变化数值较小. 当风速超过15 m/s 时，两个测试点纵向应力数值变化幅度增大且出现大幅度波动趋势. 其中测试点E05的纵向应力波动幅度较测试点W05数值较大，且其呈现纵向应力随着风速的增加而下降趋势. 测试点W05纵向应力数值曲线在风速超过20 m/s后表现为先下降后上升趋势.

分析图5（b）可知，随着风向角的增加，山区输电杆塔塔头两个测试点纵向应力均呈现波动上升趋势，但两个测试点的纵向应力受力方向不同，且两个测试点所受应力数值相差不大.

测试山区输电杆塔塔腰位置在不同风力和风向角时，其纵向应力变化情况，结果如图6所示.

分析图6（a）可知，位于山区输电杆塔塔腰位置的两个测试点纵向应力随着风速的增加而增加，但两个测试点的初始纵向应力数值不为0，原因在于塔腰位置上方存在自身应力，此时输电杆塔受风荷载和自身荷载共同作用. 在风速为0～15 m/s之间时，两个测试点的纵向应力数值完全相同，但随着风速的增加，靠近风吹来方向较近的测试点纵向应力数值较大，即测试点E03位置的纵向应力数值高于测试点W03.

分析图6（b）可知，山区输电杆塔塔腰的两个测试点纵向应力数值曲线随着风向角的增长呈现平缓波动趋势，但整体波动区间仅为2 MPa左右，波动区间较小，且两个测试点受纵向应力方向完全相反.

图6 输电杆塔塔腰应力变化Fig.6 Stress changes of transmission tower waist

测试山区输电杆塔塔腿位置在不同风力和风向角时，其纵向应力变化情况，结果如图7所示.

分析图7（a）可知，山区输电杆塔纵向应力随着风速的增加其曲线虽整体呈现上升趋势，但纵向应力上升幅度微乎其微. 两个测试点的纵向应力数值几乎相同，表明输电杆塔塔腿受风荷载力影响其纵向应力数值虽稍大，但波动幅度极其微小，其在整体结构上较为稳定.

分析图7（b）可知，输电杆塔塔腿纵向应力曲线随着风向角的变化呈现平滑状态，其趋势与塔腿纵向应力和风速关系曲线趋势大体相同，说明风向角度的变化对山区输电杆塔塔腿纵向应力影响不大.

综合分析图5～图7可知，输电杆塔塔身自下而上的纵向应力变化由大至小，但各个观测点的纵向应力波动幅度小至大. 位于水平位置的测试点纵向应力数值存在一定差别但差别数值较小. 山区输电杆塔观测点距离地面差距越大，其受风速和风向角影响越大，结构受力数值大、稳定性较差.

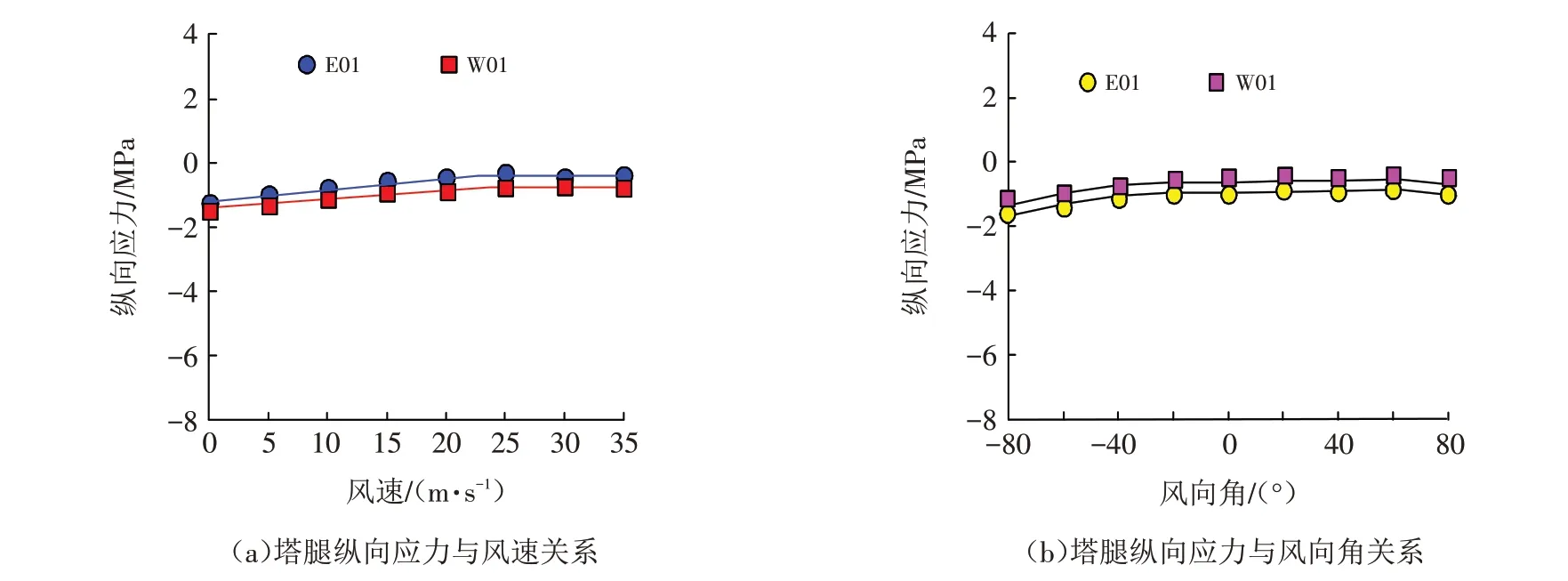
图7 输电杆塔塔腿应力变化Fig.7 Stress changes of transmission tower leg

3 结语

本文以陡峻山区输电杆塔为研究对象，通过对其进行有限元建模并使用数学算法计算其风荷载压力数值，在有限元软件内模拟对其施加不同风向角和不同速度的风，并设置不同位置观测点，分析该输电杆塔受风力荷载情况. 研究结果表明：山区输电杆塔靠近地面测试点处的纵向荷载数值较高，但其纵向荷载数值波动幅度较小；随着测试点距地面距离越来越远，输电杆塔纵向荷载力数值越来越小，但波动幅度逐渐增加.