降雨渗流场分布下边坡稳定性影响因素的探究与分析

王江平, 席红兵, 李柏生, 杨晓宇

(1.甘肃建投天水建设管理有限公司, 甘肃 天水 741000; 2.甘肃建投天水绿色装配建筑产业有限公司, 甘肃 天水 741000; 3.兰州工业学院 土木工程学院, 甘肃 兰州 730050)

边坡失稳灾害在我国非常常见，也是主要的地质灾害类型.边坡稳定性研究已有一百多年历史，一直是岩土工程的热点研究问题.极限平衡法、有限元强度折减法是目前边坡稳定性使用较为普遍的方法.经典的边坡稳定性研究多数是基于饱和土体进行的研究，而降雨引发的边坡失稳占据灾害的主导地位，边坡在降雨条件下是一个非饱和-饱和的过程，与土体的基质吸力、土水特征曲线、渗透系数的变化密切相关，而采用传统的极限平衡法或者强度折减技术，往往不能描述多孔介质的特性，使得计算结果过于保守，不利于边坡局部的应力、应变的描述，从而造成对边坡稳定性评价产生偏差.

近些年来，诸多的学者基于非饱和土理论，进行了降雨入渗条件下的边坡稳定性计算，以期获得更加真实的安全系数评价.毕仲辉等[1]采用有限元法进行降雨入渗下的边坡可靠度计算，研究了失效概率与变异系数之间的关系；杜京房等[2]考虑了干湿循环与降雨叠加作用下的边坡稳定性计算，指明了黄土的强度指标随干湿循环次数的衰减规律，以及土体残余强度的取值；刘海波等[3]进行了实际工程下的降雨入渗的数值研究；王建洪等[4]针对云南地区某堆积体边坡进行了降雨条件下的力学机理研究，并指出降雨入渗会持续改变坡体内部的应力分布，且在坡脚处最先发生应力集中现象；XU等[5]从极限分析理论出发，考虑了渗流作用对加筋土加固坡体的影响，利用非饱和土理论，建立了能量方程，从而给出了安全系数的解答.渗流导致的渗流力会对坡体稳定造成影响，考虑渗流力的影响是合理且必要的，因此，渗流-应力耦合下的计算与研究方法对于合理评价安全系数具有重要意义[6-7].李帅等[8]的研究表明渗流力对于锚杆的承载力会产生影响.谢强等[9]进行了降雨入渗过程中的渗流分析，并提出了特殊应力修正方法，能够较为准确地进行稳定性计算.不同边界条件下，渗流场的分布不同，从而导致渗流力对边坡稳定性产生不同程度的影响[10-11].许梦飞等[12]在渗流边坡的研究中考虑了土体的损伤特性，利用应力回归算法，克服了应力迭代过程中奇异点的问题.边坡在渗流作用下的稳定性评价，一直是工程人员所关心的热点问题，诸多的研究方法和理论的提出[13-17]都在不断解决这一过程中遇到的难点，如降雨强度、各向异性、不同土层特性的影响，这些问题都是边坡渗流稳定性分析中的重要组成部分，这些研究成果极大地推动了该问题的研究和发展，为实际工程的应用提供了必要的理论支撑，具有积极的作用.

在非饱和条件下，降雨入渗过程是一个非稳态的多物理场耦合问题，土体的物理性质对于稳定性计算影响是主要作用，不同的渗透系数、基质吸力都会影响到入渗过程的中每一时刻的应力场、位移场分布，不同的应力分布特性都会产生不同的安全系数结果，这对于稳定性研究有着重要的影响.此外，降雨量的不同，也会影响到边坡应力的分布.基于此，本文进行了不同的降雨量、土水特征曲线、渗透系数条件下的边坡稳定性研究(降雨过程考虑为非稳态过程，不同时刻下边坡的安全系数采用基于滑面应力的极限平衡法进行计算)，并对比了不同工况下的滑面位置的变化情况.

1 降雨入渗理论模型

Green-Ampt模型用于描述非饱和土体瞬时入渗的经典理论，该理论中土中水的渗流满足达西定律，能够满足低流速条件下的层流描述.这一模型假定土体表面与湿润锋面之间的水分是连续分布的，并且湿润区是处于饱和状态.基于上述假设，Green-Ampt模型可以表述为

(1)

式中：i为雨水的入渗速率；zf为湿润锋面的深度；h0为地表积水的深度；hf为湿润锋面的平均基质吸力水头.

在饱和入渗条件下，入渗量与湿润锋面深度之间满足式(2).

I=(θs-θi)zf

(2)

式中：I为入渗量；θi为干土的含水率；θs为饱和土体的含水率.

结合上述两式，可以得到入渗过程中，湿润锋面深度与时间t的关系式，见式(3)

(3)

土水特征曲线表明，土体含水量的大小主要取决于土体的基质吸力.边坡在降雨条件下是一个非稳态的土体逐渐吸水，从非饱和转变为饱和的过程.在满足达西定律条件下，依据势能守恒原理，可以得到坡体内某深度z处的基质吸力h(z)为

(4)

2 数值模型

2.1 模型基本参数

为了研究在不同渗透性以及不同降雨量下，坡体的孔压变化规律以及响应的安全系数，设置了四组模型以便进行对比.边坡几何模型如图1所示，坡面为排水条件，雨水能够自由入渗，边坡底部设置有地下水位浸润线，高度在10 m位置处.网格划分采用低阶四边形单元混合三角形单元.

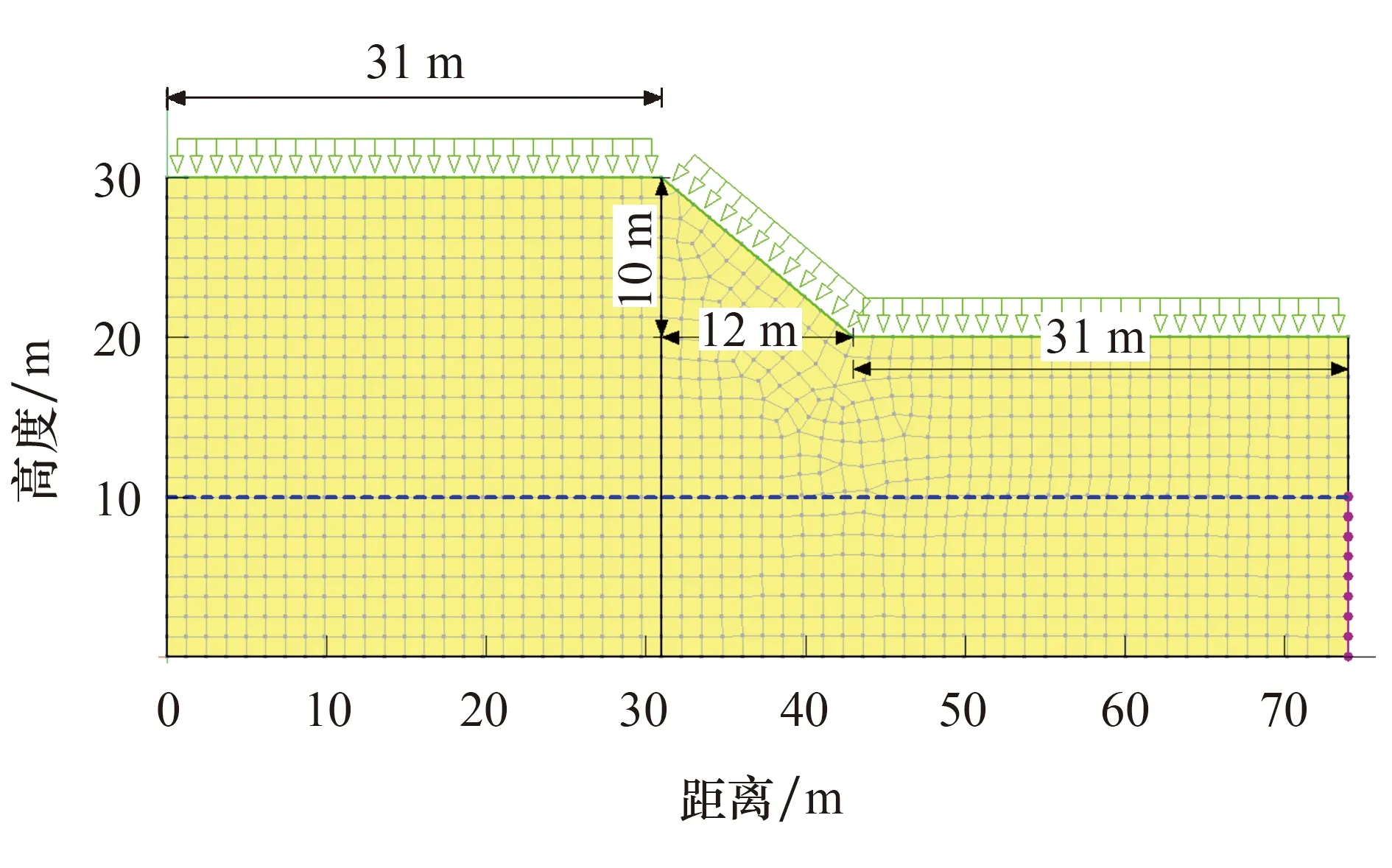
图1 边坡几何模型

土体基本物理力学参数见表1，由于边坡降雨过程为一个非饱和-饱和过程，设置土体残余含水率为0.05，降雨的持续入渗会使得土体从非饱和状态变为饱和状态，土体饱和时含水率为0.45.土体压缩系数均为1×10-5kPa，土体压缩系数会影响到土体的体积含水率.

表1 土体基本参数

土体的渗透系数分别取10-6m/s与10-4m/s，以次来探究渗透系数对于降雨条件下坡体的影响；降雨量分别选取9 mm/h和80 mm/h两种情况，分别模拟在降雨量较小情况与较大降雨量时坡体的稳定性变化规律.模型的分类及参数信息如表2所示.

表2 降雨模型参数

不同渗透系数的土体的保水性不同，采用VanGenuchten方法来估算土体体积含水率与孔压之间的关系.渗透系数较大时，土体含水率随孔压变化的幅度要大于在较小渗透系数下的幅度.越大的渗透系数对于边坡降雨作用的影响越明显.见图2所示.

依据图2的曲线，土体渗透系数与土体基质吸力之间的变化规律见图3所示，上述关系中土体饱和时渗透系数分别为表2中的数据，且残余含水率以及饱和时的含水率见表1.降雨入渗过程中，土体的含水率会发生变化，使得基质吸力也发生变化，这些因素都会影响到边坡稳定性安全系数的取值.

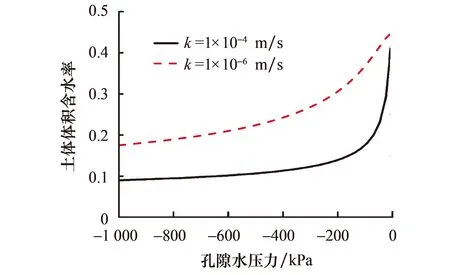
图2 土体含水率与孔压关系曲线

2.2 降雨入渗下的孔压场分布

图4为初始时刻边坡模型的孔压场分布，该时刻上部土体处于非饱和状态，因此其基质吸力较大，含水率处于最低值，基质吸力为负向孔压.依据太沙基有效应力原理可知，负孔隙水压力使得土体的有效应力增强，土体强度增大，这是有利于边坡稳定的；边坡底部下部由于地下水位的存在，土体为饱和状态，其孔压均为正孔压.

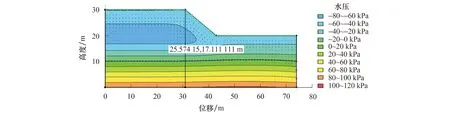
图4 初始时刻时边坡孔压分布

降雨过程是一个非稳态问题，总计算时间5 d，图5为经历5 d 9 mm/h强度的降雨后，边坡的孔压场分布.可以看到，由于降雨入渗的作用，基质吸力较大的区域面积在缩小，坡体内土体的含水率在增大.坡体在由干燥的非饱和状态转向饱和过程中，基质吸力是在持续降低的.如前所述，基质吸力的降低使得土体强度下降，边坡稳定性会随之下降.

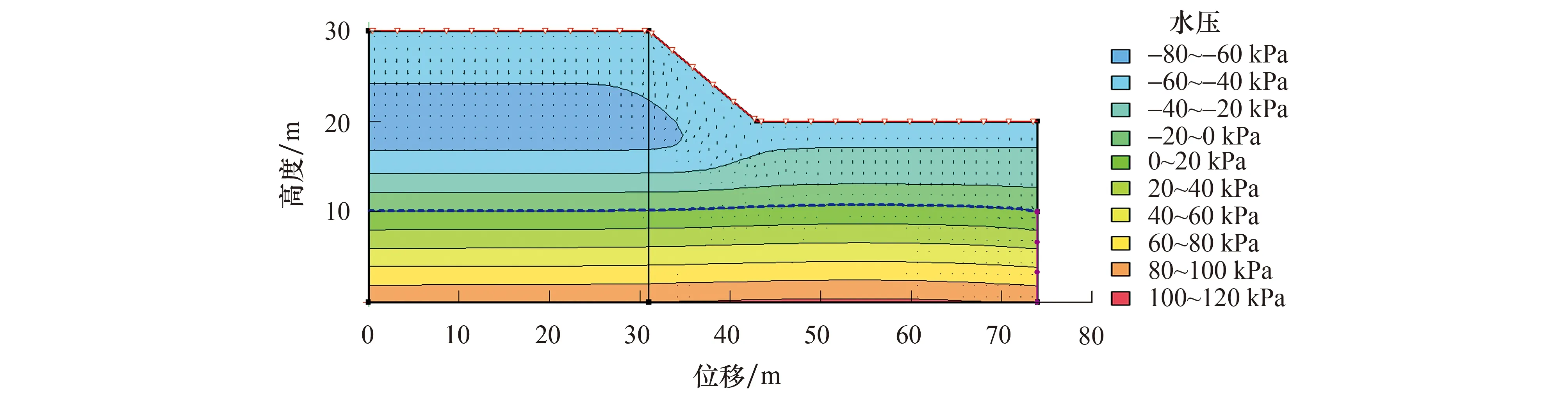
图5 降雨结束后孔压分布

图6为不同渗透系数下坡体监测点处的孔压变化曲线.选取了坡顶点、坡脚点两处作为监测点，提取了整个历时内孔压的变化曲线.对于坡顶位置，渗透系数较大时，负孔压消散幅度较小，在降雨前28 h内，差距较小，28 h后，随着降雨的继续进行，坡顶处孔压又会出现负向的增大，渗透系数越低，负向增加幅度越大；对于坡脚处的孔压变化曲线，也表现出相同的规律;渗透系数越小，坡顶、坡脚处土体的基质吸力越大，土体的强度受到基质吸力的补偿会增强，这一部分是有利于边坡稳定的，而饱和土理论中由于不考虑土体的基质吸力，会严重的低估坡体的稳定性，使得计算结果过于保守，使得治理工程经济成本增高.

图6 不同渗透性下监测点处孔压-时间曲线

当渗透系数相同而降雨强度不同时，坡顶、坡脚处两个监测的孔压变化如图7所示.在9 mm/h降雨强度下，坡顶点处的孔压幅值在初期明显小于坡脚处的，但是随着降雨的持续进行，坡顶处的孔压幅值会持续地增大，即负孔压增大，大约在70 h后，坡顶处的负孔压幅值会大于坡角处.在80 mm/h降雨强度下，亦出现相同的变化趋势，但是坡顶处变化幅度较小.降雨强度的改变对于边坡表面处的孔压影响程度低于渗透系数对于孔压的影响，因此，对于降雨条件下的边坡孔压场而言，坡体自身的土体性质占据主导地位.

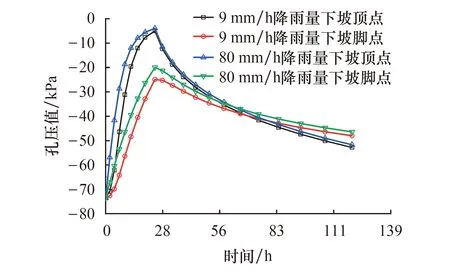
图7 不同降雨量下监测点孔压-时间曲线

2.3 不同条件下的稳定性计算

在获得边坡在降雨作用下的孔压场后，对每一个时间步的场状态采用M-P法进行稳定性计算.稳定性计算中，孔压值将直接采用前述已经获得的孔压场值.四种情况下的安全系数随时间变化规律如图8所示.对于低渗透系数模型而言，降雨强度的增大会使得安全系数降低，但降低幅度较低，初期随着雨水的入渗，安全系数持续降低，在28 h后，由于负孔压的作用，安全系数会出现回弹现象，降雨结束后，高渗透系数模型的安全系数分别为1.762与1.738.在低渗透系数情况下，较小的降雨强度时，安全系数曲线随时间的变化较为平滑，并会出现明显的回弹；而在高降雨量下，先期降低，后期出现了回弹.渗透系数越小，雨水越难以入渗到坡体内部，使得处于饱和状态的土体区域较小，土体基质吸力的发挥会更加充分.因此，安全系数会普遍的高于较大渗透系数的结果.

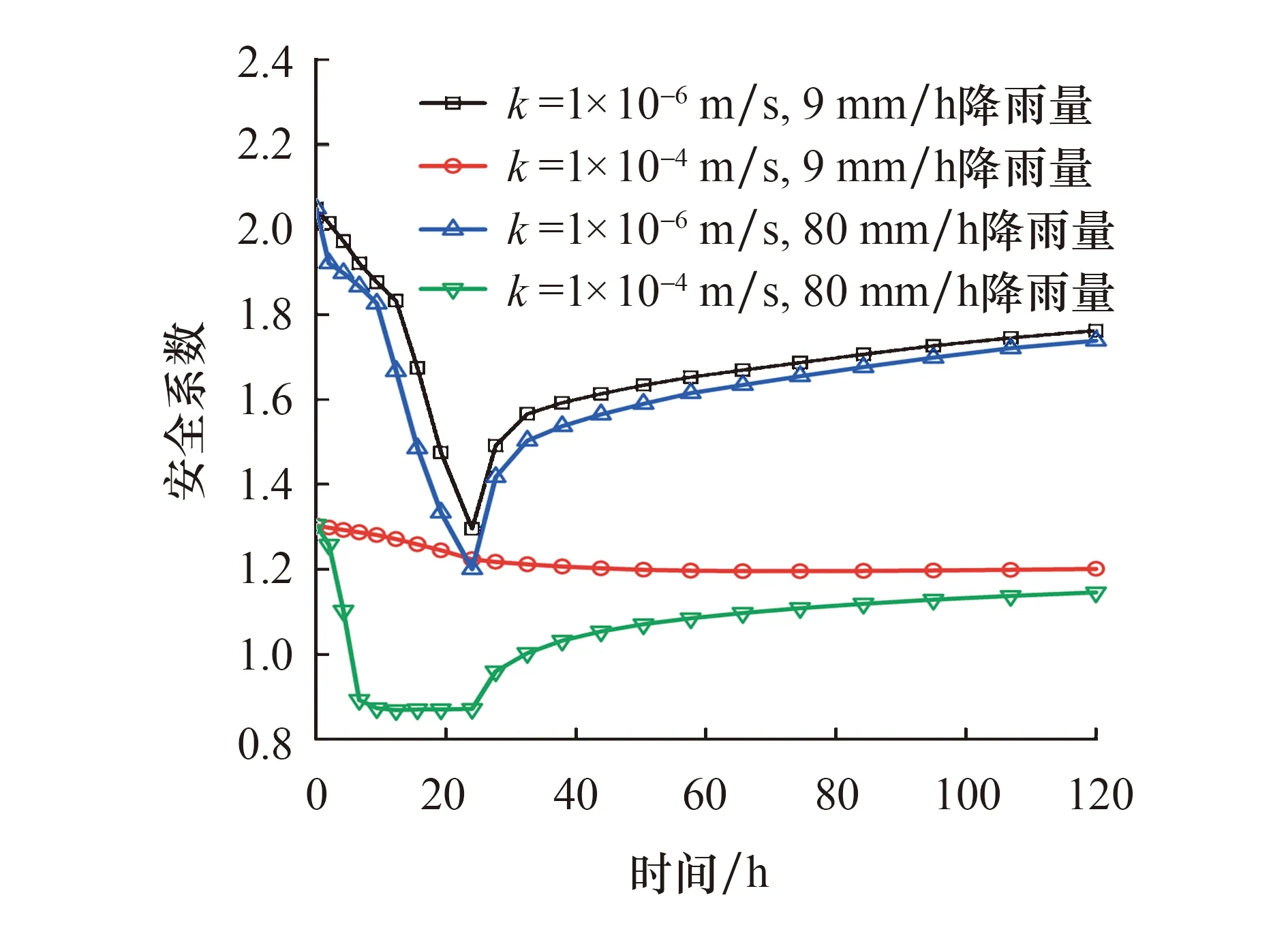
图8 安全系数-时间曲线

图9为滑面上降雨结束后土体抗剪强度的变化，可以看出，在低渗透系数下，土体抗剪强度受降雨强度影响程度较小，两个曲线基本重合，并且在滑面中部土体抗剪强度较高，在坡脚、坡顶处抗剪强度较低，大约只有最大值的三分之一.高渗透系数下，土体抗剪强度明显低于低渗透系数下的土体强度，降低幅度近50%.

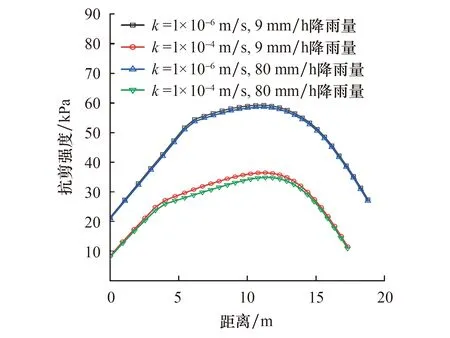
图9 滑面抗剪强度分布

图10～图11展示了降雨结束后临界滑面的位置以及对应的安全系数.低渗透系数模型中，降雨强度的增大使得安全系数从1.762降低为1.738，降低了1.36%；而在高渗透性模型下，安全系数从1.201降低到1.151，降低幅度约4.16%.在相同的降雨强度下，低渗透性模型的安全系数要明显大于高渗透性模型，对于实际工程而言，降雨对粗颗粒土质边坡的稳定性影响较大，对于渗透性较小的细颗粒土质边坡的影响较小.

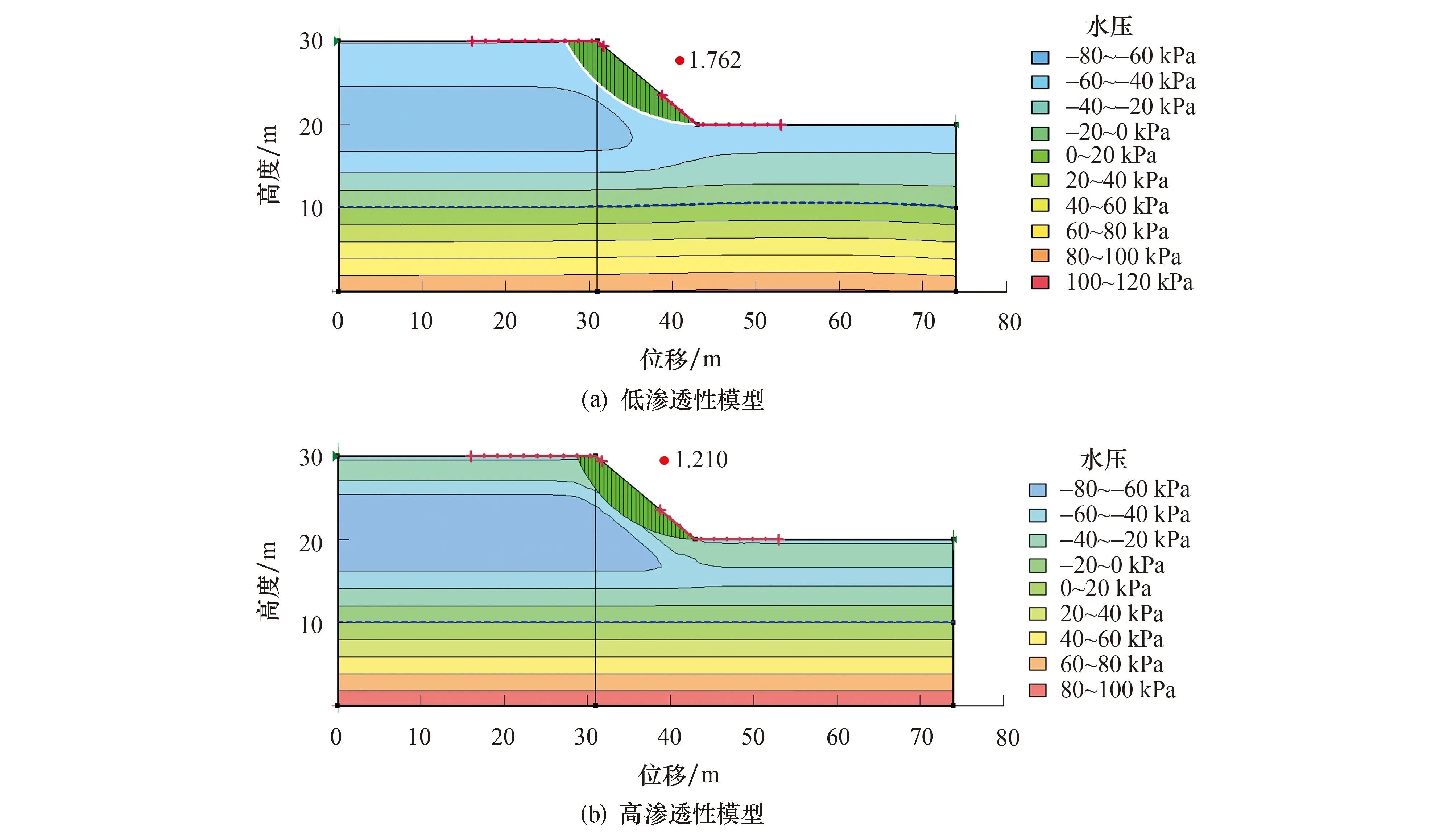
图10 模型在9 mm/h下的滑面

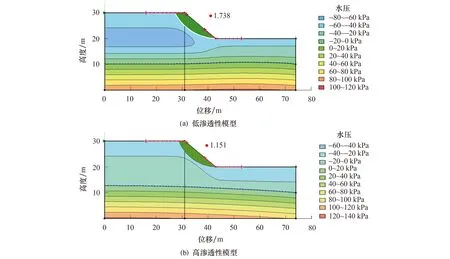
图11 模型在80 mm/h下的滑面

如果采用饱和土理论进行计算，两种降雨强度下安全系数结果为0.799与0.796，且滑面位置主要出现在坡面附近，深度较浅，但是依据非饱和土理论的计算，边坡的安全系数会出现较大程度的上升.传统理论由于缺乏对于非饱和土基质吸力贡献，会低估降雨条件下的边坡稳定性，使得治理成本增高.

3 结论

对于低渗透性土体的边坡而言，降雨过程中坡体内部的孔压变化较小，土体的基质吸力发挥程度较高，有利于边坡的稳定.而渗透性较大时，雨水的渗入使得土体饱和区域增大，基质吸力损失较大.降雨入渗作用对于高渗透性边坡影响较大，土体基质吸力会使得安全系数出现回弹变化的现象，传统计算理论会大幅度地低估边坡的安全系数.降雨条件下，依据非饱和土理论计算的结果中，不同降雨强度下，临界滑面的位置变化较小，滑面中间部位的土体抗剪强度较大，坡脚、坡顶处抗剪强度较低，在实际工程中需要注意坡脚的应力集中现象.